Dygresja: najważniejsze operatory (wyrażone we współrzędnych kartezjańskich):

Operator wektorowo-różniczkowy „nabla” (symbol
), nazywany także „operatorem gradientu”

Operator różniczkowy „nabla kwadrat” (symbol
)

(nazywany także operatorem Laplace'a lub laplasjanem - symbol Δ)

Operator Laplace'a występuje bardzo często w równaniu Schrödingera, np. dla cząstki swobodnej, zamiast pisać

, możemy napisać
, natomiast dla cząstki swobodnej poruszającej się w trzech wymiarach (x,y,z) mamy

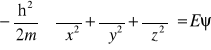
albo
Oscylator harmoniczny

Oscylatorem harmonicznym nazywamy układ, w którym na cząstkę o masie m poruszającą się wzdłuż prostej działa siła F proporcjonalna do wychylenia i skierowana do położenia równowagi.

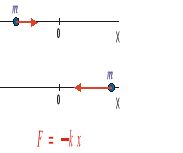
Rozważamy przypadek jednowymiarowy (kierunek x).

Siła F jest proporcjonalna do wychylenia x (przeciwnie skierowana), a współczynnik proporcjonalności k nazywamy stałą siłową.

Jak wiadomo z kursu fizyki, siła to ujemny gradient potencjału, czyli

F= -dV/dx, a zatem mamy -kx = -dV/dx, i dalej dV = kx∙dx

Całkując to równanie: ∫ dV = ∫ kx∙dx otrzymujemy V = ½kx²

czyli wyrażenie na energię potencjalną oscylatora harmonicznego.

Ponieważ energia kinetyczna oscylatora wynosi T=p_x²/2m, to całkowita energia oscylatora jest dana przez

Utworzony zgodnie z regułami Jordana operator Hamiltona dla oscylatora harmonicznego ma postać:

natomiast odpowiednie równanie Schrödingera jest następujące:

Pomnóżmy obie strony przez -2m/ħ², przenieśmy prawą stronę:

, czyli (inaczej zapisując)
. Podstawmy teraz α²=km/ħ² ; λ=2mE/ħ²

Stosując te oznaczenia możemy przepisać równanie jako:

czyli

Wprowadzamy następnie nową zmienną
otrzymując:

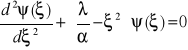
, ponieważ

(pochodna funkcji uwikłanej), więc:

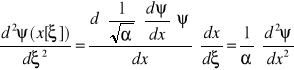
; a zatem

Mamy więc teraz równanie względem nowej zmiennej ξ (związanej z dotychczasową zmienną x poprzez wyrażenie:

Zbadajmy najpierw rozwiązania równania

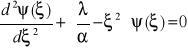
dla dużych wartości | x |.

Duże wartości | x | oznaczają zarazem duże wartości | ξ |.

Jeżeli | ξ | jest duże, to w powyższym równaniu można pominąć λ/α

Otrzymamy wówczas asymptotyczną postać równania, którego rozwiązania będą rozwiązaniami asymptotycznymi (prawdziwymi w obszarze dużych wartości | ξ | )

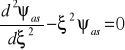
Równanie to spełnia w przybliżeniu (dla dużych | ξ |) funkcja

ψ_as = exp( ±ξ ²/ 2), co można łatwo pokazać (przez podstawienie):

Zapiszmy równanie podstawiając funkcję ψ_as = exp( ξ ²/ 2) :

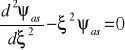
czyli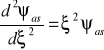

,
,

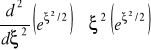
, czyli

Widać, że równanie asymptotyczne jest (w przybliżeniu) spełnione dla funkcji ψ_as = exp( ±ξ ²/ 2) - dla dużych wartości | ξ | element +1 w nawiasie jest zaniedbywalny.

Wyrażenie ψ_as = exp( ±ξ ²/ 2) opisuje w rzeczywistości dwie funkcje (jedna z dodatnim, a druga z ujemnym wykładnikiem).

Funkcję ψ_as = exp( ξ ²/ 2) (z dodatnim wykładnikiem) odrzucamy, gdyż nie jest to funkcja klasy Q (nie znika w nieskończoności). Funkcja ψ_as = exp( -ξ ²/ 2) jest natomiast funkcją klasy Q.

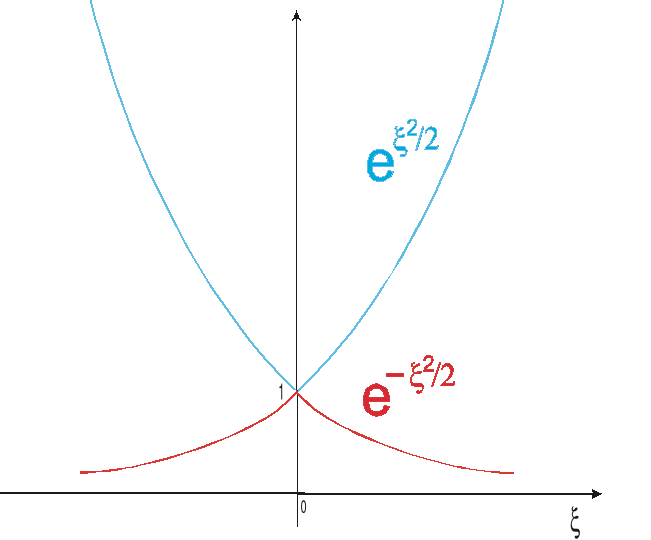
Wniosek: asymptotyczne zachowanie funkcji falowej dla oscylatora harmonicznego opisuje funkcja ψ_as = exp( -ξ ²/ 2)

Rozwiązanie asymptotyczne jest poprawne dla dużych | ξ | (czyli dla dużych | x | ). Szukamy teraz rozwiązania dla wszystkich wartości x.

Rozwiązanie to znajdziemy poprzez „poprawienie” funkcji asymptotycznej tak, aby była poprawna w całym zakresie x.

Poprawiamy funkcję asymptotyczną mnożąc ją przez pewną nową funkcję f (ξ ), czyli szukamy rozwiązań postaci ψ = ψ_as∙ f (ξ ).

Podstawiamy funkcję ψ = exp(-ξ ²/2) ∙ f (ξ ) do równania

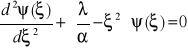
Otrzymujemy:

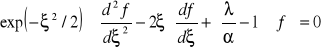
Funkcja exp(-ξ ²/2) jest zawsze różna od zera, więc równanie to może być spełnione tylko wtedy gdy

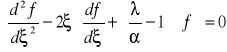
Okazuje się, że powyższe równanie należy do pewnej klasy równań różniczkowych, których rozwiązaniami są tzw. wielomiany Hermite'a

zdefiniowane wzorem

przy czym spełniony musi być warunek
, v=0, 1, 2, ...

aby pełna funkcja falowa ψ była funkcją klasy Q.

Jak łatwo zauważyć,

H₀=1; H₁=2 ξ ;

H₂=4 ξ ² -2 ; H₃= 8 ξ ³ -12 ξ  , i tak dalej.

(rzeczywiście są to wielomiany stopnia v zmiennej ξ )

Ostatecznie, funkcja falowa będąca dokładnym rozwiązaniem równania Schrödingera dla oscylatora harmonicznego jest następująca:

przy czym kwantowanie energii będzie wynikało z konieczności spełnienia warunku
(gdzie v=0, 1, 2, ...).

Jeżeli w powyższym równaniu rozpiszemy zdefiniowane wcześniej symbole λ i α, ( pamiętamy, że α²=km/ħ² ; λ=2mE/ħ² ), dostaniemy:

i dalej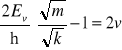
(*)

Korzystając z klasycznego wzoru na częstość drgań oscylatora:

wyznaczamy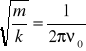

Wstawiając ostatnie równanie do równania (*) otrzymujemy

i dalej

Stąd wyrażenie na energię kwantowego oscylatora harmonicznego:

Ostatecznie:

(v = 0, 1, 2, ...)

Widać, że energia oscylatora jest skwantowana. Indeks v jest liczbą kwantową. Liczbę tę nazywamy liczbą kwantową oscylacji.

Energia oscylatora zależy od liczby v oraz od częstości ν₀ i może przyjmować tylko wartości:

E₀=½∙hν₀ (dla v=0);

E₁= ³/2∙hν₀ (dla v=1);

E₂= ⁵/2∙hν₀ (dla v=2), i tak dalej.

Widać, że odległość między sąsiednimi poziomami energetycznymi oscylatora jest stała i wynosi hν₀

Energia oscylatora kwantowego nie może być nigdy równa zeru.

Stan o najniższej możliwej energii (dla v=0) ma energię ½∙hν₀

Energia E₀=½∙hν₀ nosi nazwę zerowej energii oscylacji.

Oscylacje atomów lub jonów w kryształach zależą od temperatury

(im wyższa temperatura tym większa energia oscylacji).

Widać, że nawet w temperaturze 0 K (zero bezwzględne) oscylacje atomów (jonów) w sieci krystalicznej nie ustają (energia oscylatora jest większa od zera nawet w temperaturze T=0 K).

Oscylator harmoniczny jest stosowany w chemii jako model drgającej cząsteczki dwuatomowej (zamiast ruchu dwóch mas rozważa się wtedy ruch jednej masy, tzw. masy zredukowanej).

Oscylator klasyczny i oscylator kwantowy

1. Energia oscylatora klasycznego może być równa zeru, natomiast energia oscylatora kwantowego jest zawsze większa od zera.

2. Oscylator klasyczny może być w stanie spoczynku (masa nie porusza się). Oscylator kwantowy nie może być w stanie spoczynku (oscylacje zachodzą zawsze).

3. Największe prawdopodobieństwo znalezienia drgającej masy w oscylatorze klasycznym jest w pobliżu punktów zwrotu (maksymalne wychylenie), a w oscylatorze kwantowym w położeniu równowagi (dla małych wartości liczby kwantowej oscylacji).

4. Wraz ze wzrostem liczby kwantowej oscylacji, oscylator kwantowy staje się coraz bardziej podobny do oscylatora klasycznego (drgająca masa najczęściej przebywa w pobliżu punktów zwrotu).

5. W oscylatorze kwantowym drgająca masa (cząstka) może penetrować obszary klasycznie niedostępne (dalsze niż punkty maksymalnego wychylenia), co w oscylatorze klasycznym jest niemożliwe.

Poziomy energetyczne oscylatora kwantowego oraz odpowiadające im kwadraty funkcji falowych (linie ciągłe):

(oscylator kwantowy i klasyczny dla v=0-4, 6, 15, 24)

Efekt tunelowy

Cząstka poruszająca się w kierunku x (z energią kinetyczną p_x²/2m) zbliża się do bariery potencjału o wysokości V₀.

(Energia kinetyczna cząstki reprezentowana jest na rysunku jako wysokość, na jakiej cząstka się porusza)

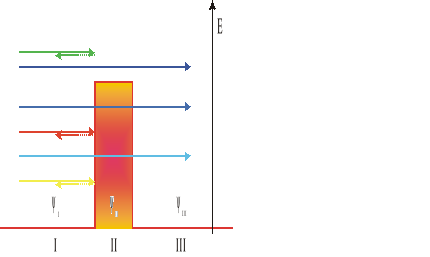
Cząstki: żółta, czerwona i zielona - odbiły się od bariery potencjału i nie osiągnęły obszaru III.

Cząstki: błękitna, niebieska i granatowa - przeszły przez barierę potencjału (obszar II) i osiągnęły obszar III.

Różnice z klasyczną barierą potencjału (brak tunelowania).

Efekt tunelowy polega na tym, że:

według mechaniki kwantowej istnieje różne od zera prawdopodobieństwo, że cząstka o energii mniejszej niż bariera potencjału, przeniknie przez barierę

oraz

według mechaniki kwantowej istnieje różne od zera prawdopodobieństwo, że cząstka o energii większej niż bariera potencjału, odbije się od bariery (nie przeniknie przez nią).

Cząstka w obszarze I jest opisywana funkcją falową cząstki swobodnej (ψ_I), gdyż w tym obszarze V=0. W obszarze III jest podobnie, chociaż funkcja falowa ψ_III jest nieco inna niż ψ_I, gdyż po przejściu przez barierę cząstka nie może już „zawrócić”.

W obszarze II należy w równaniu Schrödingera uwzględnić potencjał V₀ (czyli wysokość bariery).

Teoria efektu tunelowego - podręcznik Gołębiewskiego, str.68-70

Warto zapamiętać, że prawdopodobieństwo przejścia cząstki przez barierę zależy od: (i) wysokości bariery oraz (ii) energii cząstki

(prawdopodobieństwo przeniknięcia cząstki przez barierę rośnie wraz ze zmniejszaniem bariery i zwiększaniem energii cząstki).

Można wykazać, że dla elektronu o energii kinetycznej T zbliżającego się do bariery o wysokości V₀ , prawdopodobieństwo przeniknięcia przez barierę wynosi:

Energia elektronu Wysokość bariery Prawdopodobieństwo

T ≈½V₀ V₀ 40%

T=V₀ V₀ 67%

T=2V₀    V₀ 89%

Efekt tunelowy - przykładowe konsekwencje w fizyce i chemii

1. Rozpad jąder pierwiastków promieniotwórczych (połączony z emisją cząstek α) przebiega w oparciu o efekt tunelowy.

2. Reakcje chemiczne wymagające pokonania bariery aktywacyjnej mogą przebiegać (z ograniczoną szybkością) na drodze tunelowania (bez dostarczenia substratom wymaganej energii).

3. Stany metastabilne anionów ulegają samorzutnemu procesowi oderwania elektronu dzięki tunelowaniu.

4. Inwersja cząsteczek (np. amoniaku) od struktury piramidalnej, poprzez płaską, do piramidalnej (jedno z drgań normalnych aktywnych w podczerwieni) zachodzi dzięki efektowi tunelowemu.

54

---