Przekładnie zębate

1. Zarys odniesienia uzębień drobnomodułowych (m < 1)

Stosuje się dwa zarysy:

• bez konstrukcyjnego luzu obwodowego (s = w = 0,5⋅π⋅m) oraz

• z konstrukcyjnym luzem obwodowym (s = 0,45⋅π⋅m, w = 0,55⋅π⋅m)

Wspólne parametry obu zarysów to: y = 1, u = 1,4, α = 20^o

2. Graniczna, minimalna liczba zębów

Graniczna liczba zębów - dla danego zarysu odniesienia najmniejsza liczba zębów jaką można wykonać bez potrzeby stosowania korekcji uzębienia.

gdzie: z_g - graniczna liczba zębów, y - współczynnik wysokości głowy zęba, α - kąt zarysu; dla y = 1 i α = 20^o z_g = 17.

Minimalna liczba zębów - najmniejsza liczba zębów jaką można wykonać ze względu na zaostrzenie wierzchołka.

z_min = 8 (dla zarysu bez luzu obwodowego)

z_min = 10 (dla zarysu z luzem obwodowym)

3. Korekcja uzębienia i zazębienia

1. Korekcja technologiczna uzębienia

Jeśli liczba zębów koła z < 17, do zlikwidowania podcięcia zębów konieczne jest podczas obróbki odsunięcie zarysu narzędzia o

X = x⋅m

gdzie: x - współczynnik przesunięcia zarysu wynoszący wyznaczany ze wzoru:

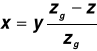
Wymiary koła korygowanego:

- średnica podziałowa: d = m⋅z,

- średnica zasadnicza: d_b = m⋅z⋅cosα,

- średnica wierzchołków: d_a = m(z + 2y + 2x),

- średnica stóp: d_f = m(z - 2u + 2x)

2. Korekcja zazębienia

1. Korekcja zazębienia typu P-0

Cechą tej korekcji jest zachowanie zerowej (czyli takiej jak w przekładni niekorygowanej) odległości osi.

Aby ten warunek był możliwy do spełnienia suma zębów współpracujących kół musi być większa lub równa podwojonej granicznej liczbie zębów, czyli

z₁ + z₂ ≥ 2 z_g

Korekcję przeprowadza się tylko wtedy, gdy jedno z kół ma liczbę zębów z₁ < z_g . Podczas wykonania kół należy narzędzie odsunąć od mniejszego koła o X oraz jednocześnie dosunąć narzędzie o taką samą wartość X do większego koła.

Wymiary kół w korygowanej przekładni

d₁ = m ·z₁ d₂ = m ·z₂

d_b1 = m · z₁ · cosα d_b2 = m · z₂ · cosα

d_a1 = m (z₁ + 2y + 2x) d_a2 = m (z₂ + 2y - 2x)

d_f1 = m (z₁ - 2u + 2x) d_f2 = m (z₂ - 2u - 2x)

a_o = 0,5 m (z₁ + z₂)

2. Korekcja zazębienia typu P

1. Korekcja typu P - technologiczna

Jej celem jest zlikwidowanie podcięcia zębów w jednym z kół oraz dobranie odległości osi a_r takiej, przy której luz obwodowy w przekładni nie ulegnie zmianie.

Warunki stosowania korekcji technologicznej typu P:

z₁ < z_g lub / i z₂ < z_g

oraz z₁ + z₂ < z_g

2. Korekcja typu P - konstrukcyjna

Przy danych parametrach kół (z₁, z₂, m) zadana jest odległość osi a_r inna niż wynikająca z obliczeń dla korekcji P-0 (a_r ≠ a_o). Należy zatem obliczyć wartości współczynników przesunięcia x₁ oraz x₂, a także wymiary kół takie, aby luz obwodowy w przekładni miał normalne wartości oraz aby nie wystąpiła interwencja zarysów.

W obu przypadkach korekcji P należy korzystać z podręczników do Podstaw Konstrukcji Maszyn lub do PKUP.

4. Przełożenie przekładni zębatej

a więc także

gdzie: ω_1,2 - prędkość kątowa s^-1, n_1,2 - prędkość obrotowa min^-1,

d_1,2 - średnice podziałowe kół, z_1,2 - liczba zębów kół

W przekładniach drobnomodułowych
, w przekładniach napędowych i ≤ 8.

Przełożenie przekładni wielostopniowej jest iloczynem przełożeń cząstkowych:

i_c = i₁⋅i₂⋅i₃ ⋅…..⋅i_n,

gdzie i_i przełożenie jednego stopnia

W przekładniach drobnomodułowych zwykle przyjmujemy rosnący ciąg przełożeń

i₁ < i₂ < i₃ < ….. < i_n

np. przełożenie i_c = 1000, można zrealizować stosując następujący rozkład przełożeń cząstkowych: i_c = 2⋅2⋅4⋅5⋅6,25

5. Podstawowe obliczenia wytrzymałościowe kół zębatych [1]

5.1. Wstępne obliczenia modułu koła

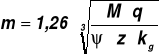
gdzie: M - moment obciążający koło w mNm (zębnika),
, (b - szerokość wieńca zębatego), dla kół drobnomodułowych zalecana jest wartość ψ = 4 ÷ 6,

q - współczynnik kształtu zęba (rys. 1), k_g - dopuszczalne naprężenia zginające (
), z - liczba zębów zębnika.

Rys. 1. Wartości współczynnika kształtu zęba q dla kół o uzębieniu zewnętrznym [1], z_n - liczba zębów koła

Materiał	stal 45	stale 25, A11, St 5	brąz B7	mosiądze MO59, MO 63
zgj MPa	300	250	120	100

5.2. Sprawdzenie naprężeń zginających u podstawy zęba

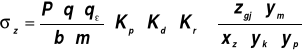
gdzie:
,
,

ε - wskaźnik zazębienia

K_p = 1,5 - współczynnik przeciążenia,

K_d = 1,2 - współczynnik nadwyżek dynamicznych,

K_r = 1,1 - współczynnik nierównomiernego rozkładu obciążenia na szerokości zęba,

- współczynnik wielkości zęba,

x_z - 1,5 ÷ 2 - współczynnik bezpieczeństwa,

y_p = 1,1 - współczynnik stanu powierzchni,

y_k = 1 - współczynnik karbu u podstawy zęba.

5.2. Sprawdzenie nacisków powierzchniowych (według Hertza)

Naprężenia ściskające maksymalne

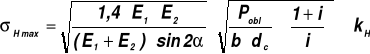
gdzie: E₁, E₂ - moduł Younga materiałów kół, α - kąt przyporu,

(dla koła czynnego),

d_c - średnica podziałowa koła czynnego,

k_H - dopuszczalne naciski powierzchniowe.

i - przełożenie;
, z₁ - liczba zębów koła czynnego.

Oznaczając:

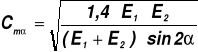
otrzymamy:

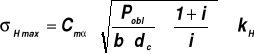
Materiał	stal 45	Stal A11	brąz B7	mosiądze MO59, MO 63
kH MPa	325	230	160	120

Jeśli: E₁ = E₂ = 2,1·10⁵ MPa (stal) to C_mα = 478,2

E₁ = 2,1·10⁵ MPa, E₂ = 1,05·10⁵ MPa (stal - brąz) to

C_mα = 390,6

Wymiar

gdzie:
- moment przenoszony przez koło czynne.

Literatura

1. Müller L.: Przekładnie zębate. Obliczenia wytrzymałościowe. WNT, Warszawa, 1972

2

---