Pompka podnośnika hydraulicznego ma rączkę w postaci dźwigni jednostronnej, ze stosunkiem długości ramion
. Stosunek promieni cylindrów podnośnika wynosi
. Jaką siłą F należy działać, aby podnieść paletę z cegłą o masie m = 900 kg?
Zadanie IV-01
Pompka podnośnika hydraulicznego ma rączkę w postaci dźwigni jednostronnej, ze stosunkiem długości ramion
. Stosunek promieni cylindrów podnośnika wynosi
. Jaką siłą F należy działać, aby podnieść paletę z cegłą o masie m = 900 kg?
Rozwiązanie:
Początek formularza
![]()
![]()
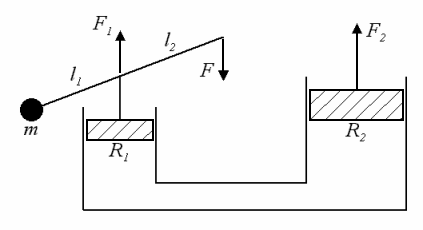
Z prawa Pascala :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Z równowagi momentów sił dla dźwigni :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zatem siła F =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-02
Naczynie w kształcie walca o promieniu r = 10 cm pływa po wodzie. Oblicz głębokość zanurzenia naczynia h, jeżeli wlano w niego V = 1 litr wody (ρW=1 g/cm3), a masa pustego naczynia wynosi m = 2 kg.
Rozwiązanie:
Początek formularza
![]()
![]()
Siła wyporu FW =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Siła ciężkości naczynia z wodą Q =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Z równowagi sił h =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-03
Oblicz z jakiej maksymalnej głębokości h można pompować wodę używając pompy ssącej? Załóż, że ciśnienie atmosferyczne wynosi p0 = 1020 hPa.
Rozwiązanie:
Początek formularza
![]()
![]()
Ciśnienie atmosferyczne wynosi wiec p0 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciśnienie hydrostatyczne na głębokości h wynosi ph =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Z równowagi ciśnień otrzymujemy h =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-04
Jaką siłą F należy rozciągać drut stalowy o przekroju S = 3 mm2, aby przywrócić mu pierwotną długość po oziębieniu go od temperatury 20oC do 10oC ( t = 10oC) . Moduł Younga dla stali wynosi E = 2x1011 Pa, a współczynnik temperaturowy = 13x10-6 K-1 .
Rozwiązanie:
Początek formularza
![]()
![]()
Z prawa Hook`a :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Oraz ze skrócenia temperaturowego pręta :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Otrzymujemy siłę F =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-05
Ile razy zmieni się siła wyporu FW działająca na kulkę aluminiową zanurzoną w wodzie, którą podgrzano o t = 10oC? Współczynnik rozszerzalności liniowej dla aluminium wynosi Al = 23x10-6 K-1, a współczynnik rozszerzalności objętościowej wody W = 21x10- 5 K-1 .
Rozwiązanie:
Początek formularza
![]()
![]()
Gęstość wody ρW =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Siła wyporu FW =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Stosunek siły wyporu w temperaturze T do siły wyporu przed podgrzaniem
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-06
Pomiaru długości dokonujemy przymiarem, którego podziałka została atestowana w temperaturze t0 = 0oC. Zmierzona długość pręta w tej temperaturze wynosi L0 = 1 m. Czy zmierzymy inną długość w temperaturze t2 = 30oC, jeżeli podziałka przymiaru wykonana jest co W = 0,5 mm, a współczynniki rozszerzalności liniowej przymiaru i pręta wynoszą odpowiednio: = 10-5 K-1 i W = 3x10-5 K-1?
Rozwiązanie:
Początek formularza
![]()
![]()
Długość wzorca w temperaturze t2, W =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Długość pręta w temperaturze t2, L =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Stosunek
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-07
W naczyniu znajduje się m = 1 kg wrzącej wody pod ciśnieniem równoważnym ciśnieniu hydrostatycznemu p = 760 mm słupa rtęci. Woda wrząc zamieniła się całkowicie w parę, bez zmiany temperatury i przy nie zmienionym ciśnieniu. Oblicz zmianę energii wewnętrznej w tym procesie.
Dane są: gęstość wody - ρW = 1 g/cm3, gęstość pary wodnej - ρP = 0,6 kg/m3, gęstość rtęci - ρR = 1,355x104 kg/m3 i ciepło parowania wody - L = 2,26x106 J/kg.
Rozwiązanie:
Początek formularza
![]()
![]()
Zmiana energii wewnętrznej jest równa:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło dostarczone do układu Q =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Praca wykonana nad układem W =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmiana energii wewnętrznej wynosi U =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-08
Drewniany klocek zsuwa się z wysokości h = 1 m po równi pochyłej o kącie nachylenia = 45o. O ile wzrośnie temperatura klocka, jeżeli = 60% ciepła wytworzonego wskutek tarcia zamieniła się w energię wewnętrzną klocka? Ciepło właściwe drewna wynosi c = 2,4 kJ/(kg K). Współczynnik tarcia wynosi f = 0,5.
Rozwiązanie:
Początek formularza
![]()
![]()
Siła tarcia T =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Praca siły tarcia W =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Przyrost temperatury klocka T =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-09
Z jaką minimalną prędkością musiałby meteor lodowy uderzyć w powierzchnię Ziemi, aby ciepło wydzielone podczas takiego zderzenia wystarczyło na stopienie całej masy lodu? Ciepło topnienia lodu wynosi L = 3,4x105 J/kg. Temperatura lodu wynosi t0 = 0oC.
Rozwiązanie:
Początek formularza
![]()
![]()
Energia wyzwolona podczas uderzenia meteoru o powierzchnię Ziemi E =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło potrzebne do stopienia lodu Q =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Minimalna prędkość meteoru VMIN =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-10
Pęcherzyk powietrza wynurzając się z dna jeziora zwiększa swoją objętość 3 razy. Oblicz głębokość jeziora h, jeżeli temperatura wody przy dnie wynosi T1 = 7oC, a na powierzchni T2 = 17oC. Ciśnienie atmosferyczne wynosi p0 = 1000 hPa.
Rozwiązanie:
Początek formularza
![]()
![]()
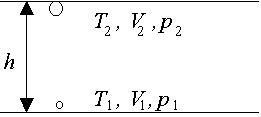
Dla stałej masy gazu doskonałego możemy napisać:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciśnienie na dnie jeziora wynosi p1 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Głębokość jeziora wynosi h =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-11
Butlę o pojemności V = 20 litrów napełniono tlenem w temperaturze T1 = 17oC do ciśnienia p1 = 107 Pa. Ile gazu ulotniło się z butli wskutek wady zaworu, jeżeli ponowne sprawdzenie ciśnienia w temperaturze T2 = 27oC dało wynik p2 = 8x106 Pa?
Rozwiązanie:
Początek formularza
![]()
![]()
Równanie stanu gazu doskonałego można zapisać w postaci:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Gęstość początkowa gazu w butli ρ1 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmiana masy gazu m =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-12
Oblicz masę tlenu w pokoju o objętości V = 50 m3 przy ciśnieniu p = 105 Pa i temperaturze T = 20oC. Dla uproszczenia załóż, że powietrze jest mieszaniną dwóch gazów (azotu i tlenu) w stosunku wagowym 4:1 . Masa molowa tlenu 1 = 32 g/mol, azotu 2 = 28 g/mol.
Rozwiązanie:
Początek formularza
![]()
![]()
Ilość moli gazu znajdującego się w pokoju n =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Równanie stanu gazu:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Masa tlenu w pokoju m1 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-13
W środku zamkniętego naczynia cylindrycznego wypełnionego gazem o objętości 2V = 2 dm3, pod ciśnieniem p = 105 Pa, znajduje się tłok o masie m = 1 kg i przekroju S = 5 cm2 . O ile przesunie się bez tarcia tłok, jeżeli cylinder porusza się wzdłuż swojej osi z przyspieszeniem a = 10 m/s2 ? Proces zachodzi w stałej temperaturze.
Rozwiązanie:
Początek formularza
![]()
![]()
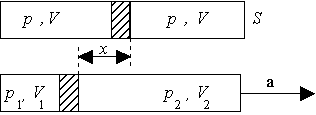
Równowaga sił działających na tłok:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciśnienie p1 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Przesunięcie tłoka x =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-14
Cylindryczne naczynie, w którym znajduje się m = 0,1 kg azotu ( = 28 g/mol), jest zamknięte od góry ruchomym tłokiem, poruszającym się bez tarcia. Aby podgrzać gaz o T = 10 K trzeba dostarczyć Q = 1050 J ciepła. Oblicz ciepło właściwe azotu przy stałym ciśnieniu - cP, pracę wykonaną przez gaz oraz zmianę jego energii wewnętrznej.
Rozwiązanie:
Początek formularza
![]()
![]()
Ciepło właściwe przy stałym ciśnieniu cP =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmianę objętości liczymy ze wzoru
, stąd V =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Praca gazu wynosi
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmiana energii wewnętrznej gazu U =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-15
Pośrodku cienkiej rurki o długości d = 1 m, zamkniętej na obu końcach i ustawionej poziomo, znajduje się słupek rtęci ( ρ = 13600 kg/m3) o długości a = 10 cm. Rurka wypełniona jest gazem pod ciśnieniem p = 105 Pa. O ile przesunie się słupek, gdy rurkę postawimy pionowo? Załóż, że temperatura układu nie zmienia się.
Rozwiązanie:
Początek formularza
![]()
![]()
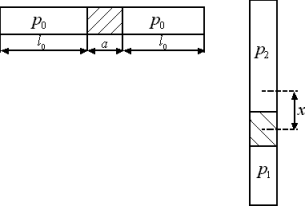
Niech x oznacza przesuniecie słupka rtęci. Z równowagi
otrzymujemy:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Z równowagi ciśnień:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Otrzymujemy równanie kwadratowe na x, którego rozwiązaniem jest:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zadanie IV-16
Ile ciepła należy dostarczyć, aby gaz zamknięty w naczyniu o objętości V = 4 dm3 zwiększył swoje ciśnienie o p = 106 Pa? Załóż, że stosunek ciepeł właściwych cP - przy stałym ciśnieniu i cV - stałej objętości wynosi = 1,4 .
Rozwiązanie:
Początek formularza
![]()
![]()
Z relacji
oraz
, otrzymujemy:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Przyrost temperatury T =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło dostarczone do układu Q =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-17
Oblicz pracę, jaką wykona n = 1 mol gazu doskonałego ogrzewany pod stałym ciśnieniem o T = 1 K.
Rozwiązanie:
Początek formularza
![]()
![]()
Praca gazu
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło dla przemiany izobarycznej Q =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmiana energii wewnętrznej U =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Stąd
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-18
Zapisz równanie adiabaty.
Rozwiązanie:
Początek formularza
![]()
![]()
We współrzędnych ( p, V ) :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
We współrzędnych ( p, T ) :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
We współrzędnych ( V, T ) :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
gdzie =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-19
Wykonano pomiary zależności ciśnienia od objętości dla przemiany adiabatycznej. Punkty eksperymentalne wykreślone w skali logarytmicznej ( log( p) w funkcji log( V)) ułożyły się na prostej o współczynniku nachylenia równym -1,4 . Ilu atomowe cząsteczki tworzą ten gaz?
Rozwiązanie:
Początek formularza
![]()
![]()
Równanie adiabaty:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zatem ln( p) =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło molowe przy stałej objętości
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co odpowiada cząsteczce o pięciu stopniach swobody. Cząsteczki gazu są więc:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-20
Określ zależność między rodzajem cząsteczek gazu doskonałego, a ciepłem właściwym gazu.
Rozwiązanie:
Początek formularza
![]()
![]()
Dla cząsteczek jednoatomowych liczba stopni swobody i parametr wynoszą:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dla cząsteczek dwuatomowych wynoszą one odpowiednio:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
a dla cząsteczek wieloatomowych:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło właściwe przy stałym ciśnieniu dla cząsteczek wieloatomowych cP =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-21
Dwa mole wieloatomowego gazu ulegają rozprężaniu izobarycznemu ze wzrostem temperatury o T = 50 K. Oblicz ilość dostarczonego ciepła Q, pracę wykonaną nad gazem W oraz zmianę energii wewnętrznej układu U.
Rozwiązanie:
Początek formularza
![]()
![]()
Ciepło
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Praca
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Zmiana energii wewnętrznej U =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-22
Oblicz sprawność cyklu silnika składającego się z dwóch izochor i dwóch izobar. Gazem roboczym jest jednoatomowy gaz doskonały, a największe ciśnienie jest dwa razy większe od najmniejszego ( pB = pC = 2 p0 ). Z kolei objętość w tym cyklu rośnie 3 razy ( VC = VD = 3V0 ).
Rozwiązanie:
Początek formularza
![]()
![]()
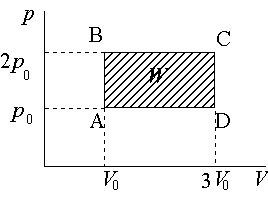
Zakładając, że temperatura w punkcie A wynosi T0 , temperatura w punktach B,C,D wynoszą odpowiednio:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło pobrane Q1 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ciepło oddane Q2 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Sprawność silnika =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-23
W kotle spalającym m = 1 tonę węgla na godzinę wytwarzana jest para wodna o temperaturze T1 = 523 K. Para ta kierowana jest najpierw do turbiny napędzającej generator prądowy o sprawności technicznej turbiny równej T = 70%, a następnie, po osiągnięciu T2 = 393 K, do chłodnicy. Oblicz maksymalną moc P, jaką można uzyskać z generatora działającego w takich warunkach. Ciepło spalania węgla wynosi L = 248x105 J/kg.
Rozwiązanie:
Początek formularza
![]()
![]()
Sprawność silnika =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Praca wykonana przez silnik W =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Moc generatora P =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
Zadanie IV-24
Ile wynosi temperatura T2 chłodnicy silnika Carnota, jeżeli temperatura grzejnicy wynosi T1 = 600 K, a silnik oddaje chłodnicy = 50% ciepła pobranego ze zbiornika ciepła?
Rozwiązanie:
Początek formularza
![]()
![]()
Sprawność silnika Carnota C =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co jest równoważne C =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Temperatura chłodnicy T2 =
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Co daje:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Dół formularza
10