Rachunek całkowy funkcji jednej zmiennej

Całka oznaczona

Dana jest funkcja
. Dzielimy przedział
punktami
tak, że
. W każdym przedziale
o długości
wybieramy dowolny punkt pośredni
. Dla tak zdefiniowanego podziału odcinka
określamy jego średnicę jako
i tzw. sumę częściową
. Na rysunku ?? przedstawiono interpretację geometryczną sumy częściowej.

Rozważmy teraz cały ciąg podziałów(zdefiniowanych jak wyżej). Powiemy, że ciąg taki jest normalny, jeśli
.

!!!!!!!!zly rysunek!!!!!!!!!!!

Definicja (całki oznaczonej). Jeśli dla każdego normalnego ciągu podziałów i dowolnie wybranych punktów pośrednich
istnieje skończona i ta sama granica
, to nazywamy ją całką oznaczoną z funkcji f w przedziale
i oznaczamy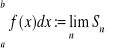
.

Uwagi. Jeśli istnieje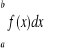
, to mówimy, że f jest całkowalna w
lub
. Zatem
oznacza zbiór wszystkich funkcji całkowalnych w
. Zamiast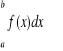
będziemy też pisać krótko
. Z definicji widać, że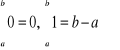
. Przyjmuje się, że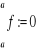
.

Twierdzenie. Funkcja ciągła w przedziale domkniętym jest całkowalna w tym przedziale. Funkcja monotoniczna w przedziale domkniętym także jest całkowalna w tym przedziale.

Twierdzenie. Jeśli funkcje
to
,
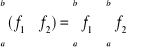
oraz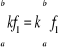
, gdzie
.

Twierdzenie. Jeżeli
oraz
to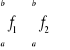
.

Twierdzenie. Jeżeli
i
, to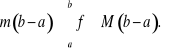

Uwagi. Patrz rys. ??.

Twierdzenie.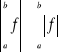
, tzn. moduł całki jest niewiększy od całki modułu.

Twierdzenie. Funkcja całkowalna w przedziale
jest także całkowalna w każdym podprzedziale domkniętym
.

Twierdzenie (addytywność całki). Jeżeli
i
, to
i
oraz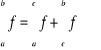
.

Uwagi. Przyjmujemy, że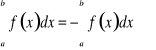
. Dzięki temu możemy powyższe twierdzenie uogólnić: jest ono prawdziwe dla dowolnej kolejności punktów a, b, c (przy założeniu, że funkcja jest całkowalna w odpowiednich przedziałach).

Przykłady.

1. Obliczyć z definicji
.

Całka ta istnieje, bo funkcja podcałkowa jest ciągła w przedziale całkowania. Dzielimy przedział
na n równych części:

. Dla n = 1, 2, ... otrzymujemy oczywiście normalny ciąg podziałów przedziału całkowania. Za punkty pośrednie obieramy punkty początkowe każdego z podprzedziałow:
.

Obliczamy wartości funkcji w tych punktach:
.

Wówczas
,

skąd

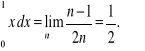
2. Obliczyć
z definicji.

Dzieląc przedział
na n równych części i biorąc za wartości pośrednie punkty początkowe podprzedziałów, otrzymujemy:

.

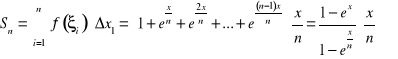
Zatem

.

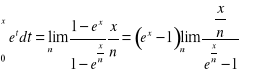
Ponieważ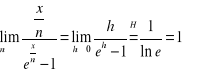
, więc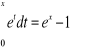
.

Załóżmy, że
. Wówczas, jak wiadomo, istnieje nie tylko całka w całym przedziale, ale również w każdym podprzedziale domkniętym. Zatem dla każdego
określona jest funkcja

.

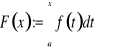
W szczególności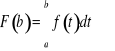
,
.

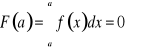
Przy założeniu, że
, funkcja
ma określony sens geometryczny (rys. ??). W tej interpretacji
jest polem trapezu krzywoliniowego AB'C'D.

Twierdzenie. Jeśli
, to funkcja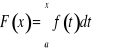
jest ciągła w
.

Twierdzenie (o wartości średniej dla całek). Jeżeli
to istnieje w tym przedziale punkt
, dla którego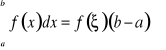
.

Dowód. Jeżeli m oznacza najmniejszą wartość funkcji w danym przedziale, a M oznacza wartość największą, to

,

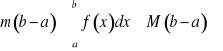
czyli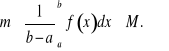
Jeżeli oznaczymy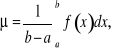
to
Stąd wobec ciągłości funkcji i własności Darboux istnieje w przedziale
taki punkt
, że
. Podstawiając za liczbę
podaną wartość dostajemy

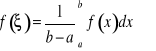
. KD.

Twierdzenie. Jeżeli
oraz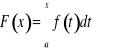
, to
jest funkcją różniczkowalną w
i
dla
.

Dowód. Niech
. Wówczas

,

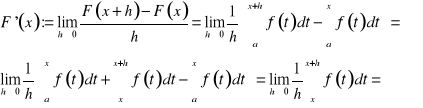
gdzie c leży między x i x+h. Skorzystaliśmy tu m. in. z twierdzenia o wartości średniej dla całek i z założenia o ciągłości f .

Definicja. G nazywamy funkcją pierwotną dla f w
, jeśli
.

Uwagi. Pokazaliśmy zatem, że każda funkcja ciągła w domkniętym przedziale ma w nim funkcję pierwotną.

Twierdzenie (zasadnicze rachunku całkowego, związek całki oznaczonej z nieoznaczoną). Jeśli
i istnieje funkcja F pierwotna dla f w
, to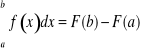
.

Uwagi. Notacja alternatywna: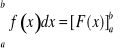
.

Całka nieoznaczona

Funkcją pierwotną dla danej funkcji f nazywaliśmy funkcję różniczkowalną F taką, że
. Ponieważ dla dowolnej stałej C,
więc każda funkcja różniąca się od danej funkcji pierwotnej o dowolna stałą też jest funkcją pierwotną dla f. Zatem dana funkcja f wyznacza klasę swych funkcji pierwotnych, które różnią się między sobą o stałą. Na przykład funkcją pierwotną dla funkcji
w dowolnym przedziale jest funkcja
x³/3, a klasą wszystkich funkcji pierwotnych dla f jest zbiór

Definicja. Zbiór wszystkich funkcji pierwotnych dla danej funkcji
nazywamy całką nieoznaczoną z f . Całkę nieoznaczoną funkcji
oznaczamy symbolem
. Zatem

.

Uwagi. Różniczkowanie, czyli obliczanie pochodnej jest działaniem jednoznacznym, natomiast działanie odwrotne, całkowanie, czyli szukanie funkcji pierwotnej jest działaniem wieloznacznym z dokładnością do stałej. W symbolu całki nieoznaczonej
funkcję
nazywamy funkcją podcałkową. Z poprzednich twierdzeń wynika, że każda funkcja ciągła (w określonym przedziale) ma funkcję pierwotną, a więc dla każdej funkcji ciągłej istnieje również całka nieoznaczona.

Z definicji całki wynika, że różniczkowanie i całkowanie są operacjami do siebie odwrotnymi, a dokładniej:

,
,

Przykłady.

, bo
.

, bo
.

, bo
.

, bo
.

, bo
.

, bo
.

Wzory podstawowe dla całek nieoznaczonych (dowód polega na zróżniczkowaniu prawych stron: wynikiem powinna być funkcja podcałkowa z lewej strony):

dla dowolnej liczby rzeczywistej
,

,

,

,

dla dowolnej liczby rzeczywistej
,

Uwagi. Prawdziwe są następujące wzory:

, bo

bo

Przykłady.

1.

.

2.
.

3.

.

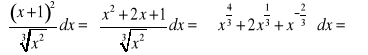
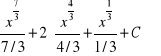
Twierdzenie (całkowanie przez części). Jeśli
, to
.

Dowód. Należy pokazać, że
. Obliczamy pochodną
, skąd wynika teza. KD.

Przykłady.

1.

.

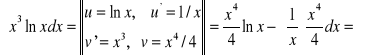
2.
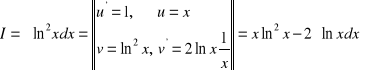
. Ponadto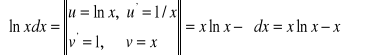
. Zatem
.

3. Obliczyć
.

Wiadomo, że
. Dla
mamy

.

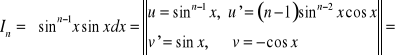
Zatem
Stąd
i ostatecznie dostajemy wzór rekurencyjny

.

Twierdzenie (całkowanie przez podstawianie). Jeżeli
,
,
, to
.

Przykłady.

1. Obliczamy całkę
.

Wprowadźmy nową zmienną całkowania t za pomocą podstawienia
Wówczas
. Otrzymujemy: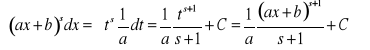
.

2.

.

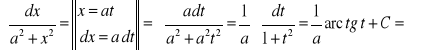
3.

.

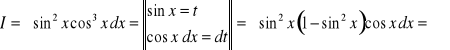
4.
.

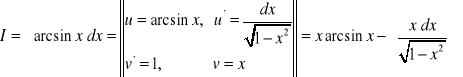
Obliczamy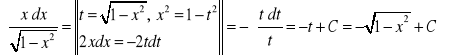
, a zatem
.

Często wygodnie jest stosować następujące wzory:

(88)
.

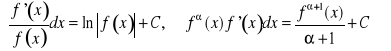
Ich prawdziwość można udowodnić różniczkując wzory stronami.

5.

6.
,
(ZD).

Dla całki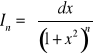
wyprowadzimy teraz wzór rekurencyjny.

(5)
,

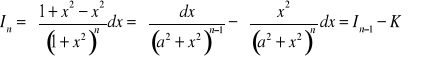
gdzie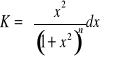
.

Całkujemy przez części, przyjmując:

.

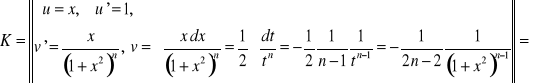
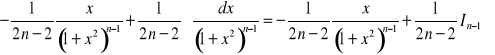
Podstawiamy do (5) i otrzymujemy:

.

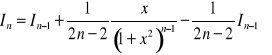
Ostatecznie wzór rekurencyjny ma postać:

(99)
.

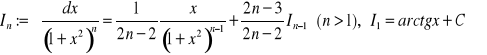
W ten sposób omówiliśmy ogólne metody całkowania. Metody całkowania pewnych klas funkcji (wymiernych, niewymiernych i trygonometrycznych) zamieszczono w Dodatku 1.

Definicja całki niewłaściwej

Definicja. Niech
/
/. Punkt b /a/ jest punktem

osobliwym tej funkcji, jeśli (
i
) albo
/(
i
) albo
/.

Rys. ?? Rys. ??

Rys. Rys.

Na rysunku ?? są zilustrowane te przypadki, gdy b lub a są skończonymi punktami osobliwymi, natomiast rys. ?? dotyczy przypadku gdy
. Może się również zdarzyć, że równocześnie a i b są punktami osobliwymi. Będzie tak wówczas, gdy
i

1.
albo
,

2.
albo
.

Rysunek ?? ilustruje przypadek, gdy a i b są skończonymi punktami osobliwymi funkcji.

Podamy teraz definicję całki niewłaściwej.

Definicja. Jeżeli b [a] jest punktem osobliwym funkcji
, to całką niewłaściwą tej funkcji w przedziale
nazywamy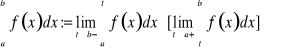
,

o ile granica ta jest skończona.

Uwagi. Jeżeli a i b są punktami osobliwymi funkcji, to całką niewłaściwą nazywamy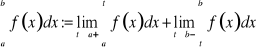
, o ile obie granice są skończone.

Jeśli w szczególności
,
to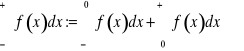
.

Interpretacja geometryczna: jeśli
i a lub b są osobliwe, to

całka niewłaściwa
jest równa polu figury (nieograniczonej w poziomie lub w pionie) pod wykresem f (patrz rysunki ??).

Przykłady.

a)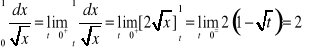
.

b)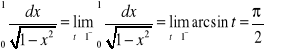
.

c)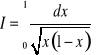
. Ponieważ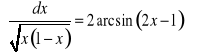
, to

.

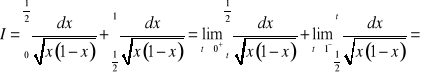
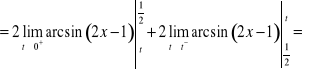
Zastosowania geometryczne całek oznaczonych

Pole figury płaskiej

Rozpatrzmy figurę ABCD określoną w następujący sposób:

(rys ??). Jak widać, pole tej figury

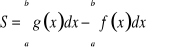
czyli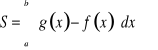
.

Rys. Rys.

Przykłady. Obliczyć pole figury płaskiej wyciętej przez elipsę
.

Z równania elipsy znajdujemy równanie górnej połowy elipsy:
.

Szukane pole wynosi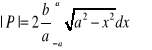
. Można teraz obliczać
, ale prościej jest zauważyć, że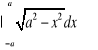
jest równa połowie pola koła
. Zatem
.

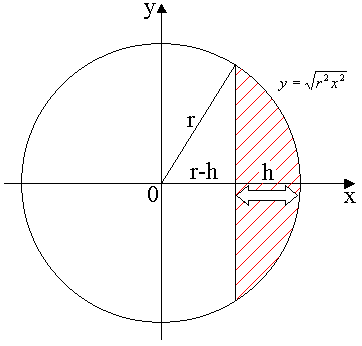
Objętość bryły

Rozpatrzmy bryłę zawartą między dwiema płaszczyznami prostopadłymi do osi OX i przecinającymi tę oś odpowiednio w punktach
i
(rys. ??). Przypuśćmy, że znamy pole przekroju tej bryły dowolną płaszczyzną prostopadłą do osi OX. Pole to jest więc daną funkcją
określoną i ograniczoną w przedziale
. Można pokazać, że wtedy

.

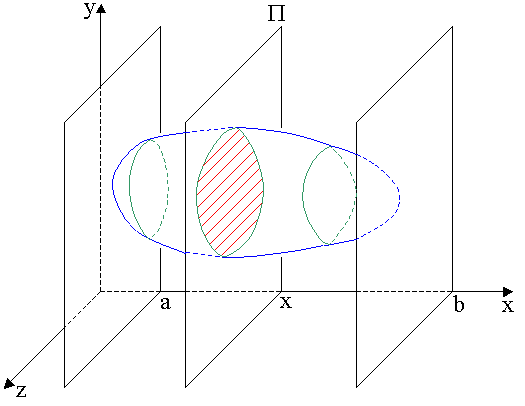
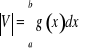
Przykłady.

Obliczyć objętość elipsoidy (rys. ??).

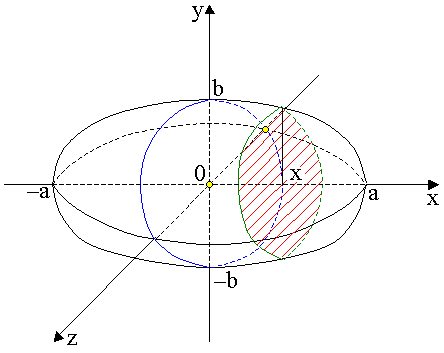
Powierzchnia elipsoidy ma równanie
. Jej przekrój płaszczyzną

Rys.

prostopadłą do osi OX w dowolnym punkcie jest elipsą o równaniu
, czyli

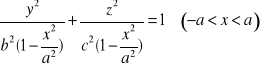
Ponieważ półosie tej elipsy są równe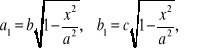
więc pole przez nią wycięte wynosi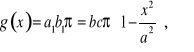
przy czym
. Szukana objętość jest równa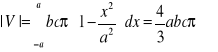
.

Dla
otrzymujemy kulę, a jej objętość
.

Pole figury obrotowej

Przypuśćmy, że figura ABCD ograniczona krzywą o równaniu
, osią OX i prostymi x=a oraz x=b (a < b), obraca się dookoła osi OX (rys ??).

Wtedy przekrój tej bryły dowolną płaszczyzną prostopadłą do osi OX przechodzącą przez punkt
jest kołem o promieniu
, pole tego

Rys. ??

przekroju
a stąd otrzymujemy wzór na objętość bryły obrotowej

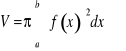
lub krócej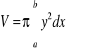
.

Przykłady.

1. Jeżeli elipsa o równaniu
obraca się około osi OX, to powstaje elipsoida obrotowa wydłużona. Z równania elipsy mamy
a więc

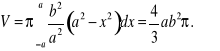
Gdy obrót odbywa się około osi OY wtedy powstaje elipsoida obrotowa spłaszczona. Ponieważ
więc

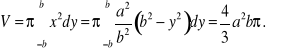
2. Oblicz objętości torusa, tj. obręczy kołowej powstałej przez obrót okręgu o promieniu r około prostej leżącej w płaszczyźnie tego koła i nie przecinającej go (rys. 1.40).

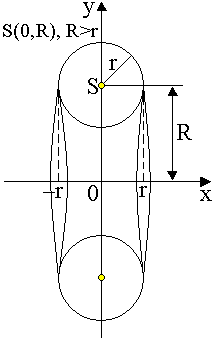
Niech R będzie odległością osi obrotu od środka koła obracającego się i R > r. Obracający się okrąg ma w przyjętym układzie współrzędnych równanie
Stąd górny półokrąg ma równanie
a dolny
Niech

Objętość powstałej bryły

.

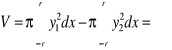
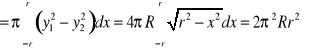
Rys. 1.40

3. Objętość bryły powstałej przez obrót cosinusoidy około osi OX w przedziale
wynosi

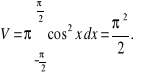
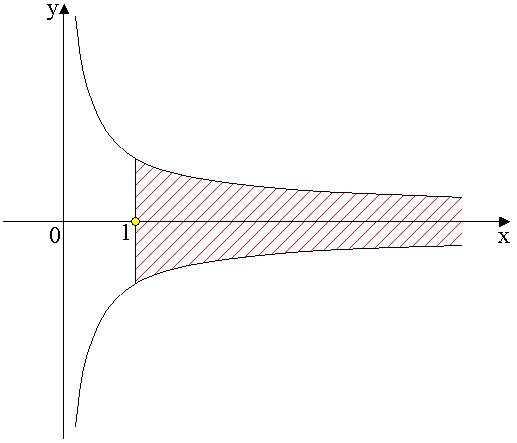
4. Obliczyć objętość bryły powstałej przez obrót hiperboli równoosiowej
dla
(rys. ??).

Powstała bryła jest nieograniczona. Jej objętość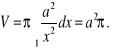

Długość krzywej

Niech dana będzie płaska krzywa w postaci parametrycznej

.

Można udowodnić następujące

Twierdzenie. Jeżeli
, to krzywa K posiada długość

.

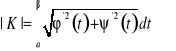
Przykłady.

1. Obliczyć długość okręgu
.

Okrąg ten ma równania parametryczne

,

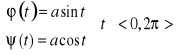
a zatem jego długość jest równa

.

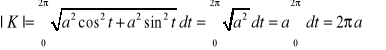
2. Obliczamy długość krzywej K o równaniach
dla
. Ponieważ
, więc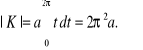

Przypuśćmy, że krzywa K jest określona równaniem funkcyjnym
dla
, przy czym
. Wówczas równania
dla
są równaniami parametrycznymi tej krzywej. Do obliczenia jej długości zastosujemy wobec tego wzór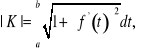
czyli

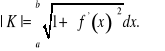
Przykłady.

Za pomocą ostatniego wzoru obliczymy jeszcze raz obwód koła. Z równania okręgu
otrzymujemy rownanie jego górnej połówki
.

Stąd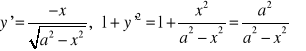
i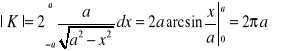
.

Podobnie jak w przypadku płaskim mamy dla krzywej przestrzennej następujące

Twierdzenie. Jeżeli
,
, to krzywa przestrzenna K ma długość i wyraża się ona wzorem:

.

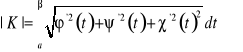
Przykłady.

1. Długość linii śrubowej o równaniach
dla
wynosi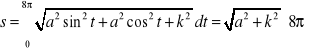
.

Pole powierzchni obrotowej

Gdy krzywa o równaniach
dla
obraca się dookoła osi Ox, wówczas zakreśla pewna powierzchnię obrotową, której pole można obliczyć za pomocą całki oznaczonej. Jeśli
, to pole to istnieje i jest równe:

(1)
.

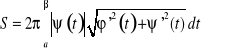
Jeżeli obracająca się krzywa ma równanie
, przy czym
, to wzór (1) przyjmuje postać:

(1')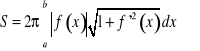
.

Przykłady.

1. Obliczyć pole powierzchni torusa (rys. 1.40). Z równań okręgu tworzącego w wyniku obrotu torus otrzymujemy: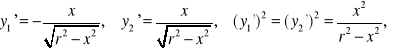

Pole
gdzie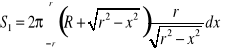
,
.

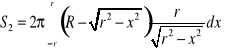
Zatem

.

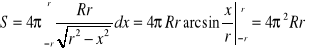
Możemy to zadanie rozwiązać też innym sposobem. Równania parametryczne obracającego się okręgu są następujące:
. Stąd
i pole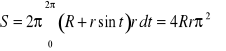
.

2. Wyprowadzimy wzór na pole powierzchni czaszy kuli (rys. 1.45).

Rozpatrujemy łuk
dla
Obliczamy
, skąd

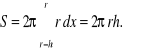
Z ostatniego wzoru dla
dostajemy wzór na pole kuli:
.

Przybliżone obliczanie całek oznaczonych - metoda trapezów

!!!!!!!!!!BRAK RYSUNKU !!!!!!!!!

Metoda trapezów polega na tym, że figurę ABCD zastępujemy figurą złożoną z trapezów wpisanych (rys. 1.59), tzn. krzywą aproksymujemy linią łamaną w nią wpisaną. Przedział całkowania dzielimy przy tym na równe części. Oznaczmy
. Wówczas pole figury złożonej z trapezów wynosi

,

gdzie
.

Stąd otrzymujemy wzór przybliżony w metodzie trapezów:

.

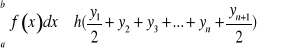
Można pokazać następujące oszacowanie błędu tej metody:

,

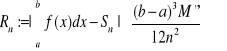
gdzie
.

Dodatek 1. Całkowanie pewnych klas funkcji.

Całkowanie funkcji wymiernych

Do obliczenia jest całka
, gdzie
są wielomianami zmiennej x stopnia n i m odpowiednio. Jeśli
, to należy podzielić wielomiany w wyniku czego dostaniemy
. Zatem zawsze do obliczenia zostaje całka postaci

(22)
.

Znajdujemy wszystkie miejsca zerowe wielomianu
. Wówczas wielomian ten da się zapisać w postaci iloczynowej, czyli iloczynu czynników 1. stopnia lub 2. stopnia
, przy czym niektóre czynniki mogą występować wielokrotnie (np. czynnik
oznacza, że a jest s-krotnym pierwiastkiem wielomianu
).

Twierdzenie (o rozkładzie funkcji wymiernej na ułamki proste). Funkcja wymierna postaci
da się zapisać w postaci sumy tzw. ułamków prostych, które odpowiadają czynnikom w rozkładzie iloczynowym mianownika według następującej tabeli:

Czynnik Odpowiadające mu ułamki proste

Zatem całka (22) sprowadza się do sumy całek z ułamków prostych. Zauważmy, że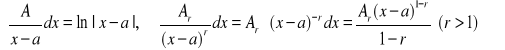
.

Całkę
obliczamy sprowadzając trójmian kwadratowy do postaci kanonicznej. Podobnie obliczamy całkę
, dodatkowo stosując wzór rekurencyjny (99) (patrz przykłady niżej).

Wniosek. Każdą funkcję wymierną można zcałkować.

Przykłady.

1.

.

2.

.

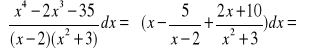
3.

,

gdzie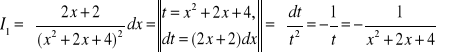
,

.

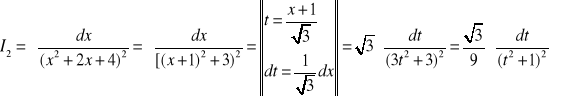
Ze wzoru rekurencyjnego (99) mamy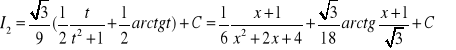
.

Wstawiamy do wzoru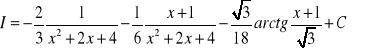
.

Całkowanie funkcji niewymiernych

Ogólna metoda całkowania funkcji niewymiernych polega na zastosowaniu odpowiedniego podstawienia, po którym sprowadzamy daną całkę z funkcji niewymiernej do całki z funkcji wymiernej. Umiemy całkować tylko niektóre typy funkcji niewymiernych. Tutaj podamy podstawienia dla następujących typów funkcji:

(A)
,

gdzie R jest funkcją wymierną k+1 zmiennych,
, W - zbiór liczb wymiernych oraz
, do której stosujemy podstawienie

,

przy czym n jest najmniejszą wspólną wielokrotnością mianowników liczb
;

(B)
,

gdzie
, sprowadzamy do całki z funkcji wymiernej w następujących przypadkach:

a)
, Z - zbiór liczb całkowitych, podstawiamy
, gdzie k jest wspólnym mianownikiem ułamków r i s,

b)
, podstawiamy
, gdzie n jest mianownikiem ułamka p,

c)
, podstawiamy
, gdzie n jest mianownikiem ułamka p.

(C)
,

po sprowadzeniu trójmianu kwadratowego Y do postaci kanonicznej dostajemy całkę, którą można obliczyć natychmiast stosując wzory podstawowe dla całek nieoznaczonych;

(D)
,

stosujemy tu wzór
, z którego po zróżniczkowaniu obu stron i pomnożeniu ich przez
otrzymujemy równość dwóch wielomianów, obliczamy współczynnik A oraz współczynniki wielomianu
, zaś całkę
obliczamy jak w (C).

Przykłady.

1. Obliczyć całkę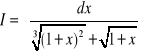
. Mamy tu
więc n=6. Zatem
,

.

2.

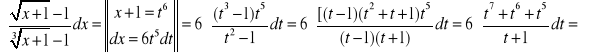
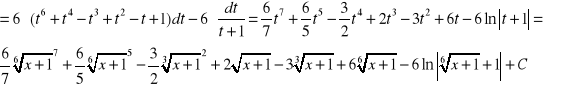
3.

.

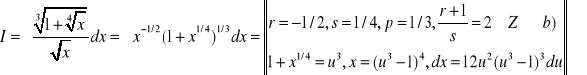
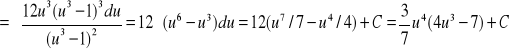
4.
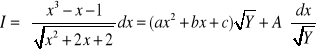
, gdzie
.

Różniczkując obie strony dostajemy

.

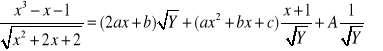
Po pomnożeniu obu stron przez
mamy
, skąd obliczamy

. Zatem

. Obliczamy jeszcze całkę

.

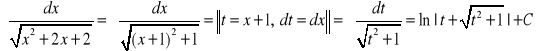
5. Obliczyć całkę
(ZD)

(Wskazówka: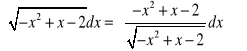
).

Całkowanie funkcji trygonometrycznych

Ogólna metoda całkowania funkcji trygonometrycznych polega na zastosowaniu odpowiedniego podstawienia, po którym sprowadzamy daną całkę z funkcji trygonometrycznej do całki z funkcji wymiernej. Umiemy całkować tylko niektóre typy funkcji trygonometrycznych. Tutaj podamy podstawienia dla następujących typów funkcji:

(E)
.

gdzie R jest funkcją wymierną. Stosujemy poniższe podstawienie
, skąd
,
oraz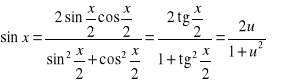
,
.

(F)
,

stosujemy tu podstawienie
, skąd
,
oraz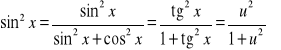
,
,
.

(Ga)
,

(Gb)
,

W przypadku (Ga) podstawiamy
, skąd
, zaś w przypadku (Gb) podstawiamy
, skąd
.

Przykłady.

1. Całkę
można obliczyć trzema sposobami: (E), (F) i (Ga).

(E): podstawiamy
, skąd
,
,
. Zatem

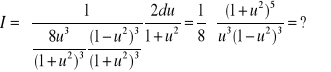
(ZD).

(F):
, podstawiamy
, skąd
,
. Zatem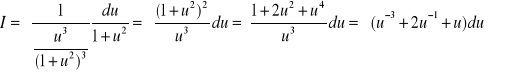

.

(Ga):
, zatem podstawiamy
, skąd
. Mamy więc
(ZD).

Jak widać, metoda (F) okazała się najprostsza.

1