Badania skał w trójosiowym stanie naprężeń ściskających.
1.Cel ćwiczenia:
Odwzorowanie stanu naprężeń istniejących w górotworze w celu wykonani charakterystyk kryteriów wytrzymałościowych do zbudowania modelu górotworu.
Określenie funkcji: ![]()
2. Pierwotny stan naprężeń w górotworze nienaruszonym działalnością górniczą.
Ustalenie pierwotnego stanu naprężeń i odkształceń w górotworze nienaruszonym działalnością górniczą stanowi punkt wyjścia do wszelkich rozważań geomechaniki. Wynika to z faktu, że z chwilą wkroczenia robotami górniczymi do masywu górotworu, wszelkie zmiany mechaniczne w nim zachodzące odnosić się będą do stanu pierwotnego.
W celu wyznaczenia składowych pierwotnego stanu naprężenia i odkształcenia przeanalizować należy elementarną cząstkę górotworu o kształcie sześcianu wyciętą z masywu skorupy ziemskiej na głębokości H.
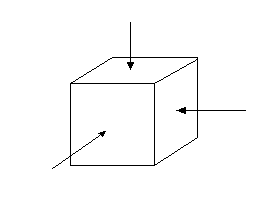
Rysunek 1.Składowe pierwotnego stanu naprężenia w górotworze.
Ta elementarna cząstka jest obciążona w kierunku pionowym ciężarem nadkładu wywołującym ciśnienie pionowe o wartości:
![]()
gdzie: ![]()
- ciężar objętościowy skał nadkładowych.
Pod wpływem ciśnienia ![]()
i wobec braku możliwości odkształcenia się elementarnego sześcianu w płaszczyźnie poziomej, na jego powierzchniach pionowych pojawiają się symetrycznie równe ciśnienia poziome ![]()
, których wartość wynika z uogólnionego prawa Hooke`a:
![]()
Stąd ciśnienie poziome działające na boczne ścianki wynosi:
![]()
gdzie: ![]()
- współczynnik Poissona.
W rzeczywistości jednak taki stan naprężeń nie występuje gdyż zazwyczaj ![]()
.
Tak więc złożoność warunków i stanów obciążeń skał występujących w pionowym profilu litologicznym wymaga określenia ich własności mechanicznych w trójosiowym stanie naprężeń.
Warunki obciążenia skał w górotworze i zbadanie ich mechanicznych własności jest możliwe w laboratorium przy zastosowaniu specjalnych urządzeń ciśnieniowych zezwalających na modelowanie stanów naprężeń zbliżonych do warunków naturalnych.
Badania skal w warunkach wszechstronnych naprężeń ściskających dostarczają również informacji o mechanizmie ich niszczenia, które jest opisane kryterium wytrzymałościowym.
3. Przebieg doświadczenia:
Zróżnicowanie składowych stanu naprężenia osiągnięto poddając próbkę skalną działaniu wszechstronnego ciśnienia. Zastosowano więc zasadę Karmana, wg której na jednoosiowy stan naprężenia (ciśnienie pionowe ![]()
) nakłada się hydrostatyczny stan ciśnień (ciśnienie boczne ![]()
) przy czym ![]()
.
Badanie przeprowadzono na próbkach walcowych o smukłości ![]()
, dla których większe naprężenie główne ![]()
jest przykładane zgodnie z osią pionową próbki, natomiast mniejsze naprężenie główne ![]()
oddziaływują na obwodzie próbki w kierunku radialnym.
Próbkę skalną umieszcza się w osłonie gumowej dla ochrony przed penetracją oleju i zamyka się w szczelnej komorze ciśnieniowej w której realizowany jest osiowo symetryczny stan naprężeń. Ciśnienie boczne ![]()
wytworzone jest przez olej, natomiast ciśnienie pionowe ![]()
wywoływane jest mechanicznie przez maszynę wytrzymałościową ze stałą prędkością wynoszącą 0,2 MPa/s.
Cały cykl badawczy został przeprowadzony w postaci testu klasycznego który polegał na:
Zadaniu określonego ciśnienia bocznego które było utrzymywane na stałym poziomie, a następnie doprowadzaniu ciśnienia pionowego aż do zniszczenia próbki. Czynność ta powtórzona została kilkakrotnie.
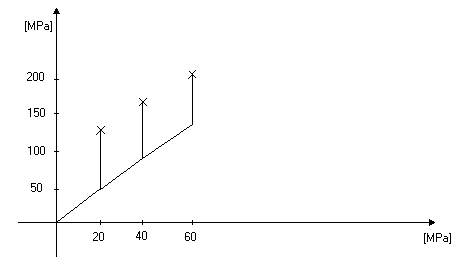
Wartości zadawanych ciśnień poziomych zależą od wytrzymałości skały, dla skał słabych stosuje się ciśnienia rzędu 5-10MPa, natomiast dla skal mocnych 20-60MPa.
Wykres1. 1. Test klasyczny.
Oprócz opisanego wyżej testu stosuje się także test wielokrotnego zniszczenia, który polega na tym że próba skalna na początku tak jak w poprzednim przypadku zostaje obciążona ciśnieniem bocznym następnie pionowym jednak tym razem nie zostaje zniszczona ponieważ tuż przed zniszczeniem ciśnienie pionowe przestaje być zwiększane, a dodawane jest po raz kolejny ciśnienie boczne, które rozpoczyna następny cykl obciążania próbki.
Zaletą takiego typu testu jest to że jest on wykonywany na jednej próbce.
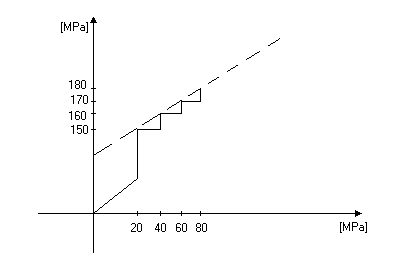
Wykres1. 2. Test wielokrotnego zniszczenia.
Innym typem testu jest test ciągłego zniszczenia który polega na tym iż próbka poddawana jest równocześnie ciśnieniu bocznemu jak i pionowemu.
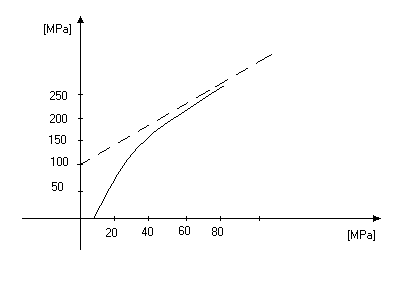
Wykres1. 3. Test ciągłego zniszczenia.
4. Opracowanie wyników na podstawie kryteriów wytrzymałościowych.
Przez kryterium wytrzymałościowe rozumieć będziemy zarówno utratę ciągłości skał w skutek pęknięć, przełamów itp., jak i wystąpienie dużych i nieodwracalnych odkształceń prowadzących do utraty stateczności lub funkcjonalności wyrobisk górniczych.
Spośród licznych kryteriów wytrzymałości wymienić należy kryterium de Saint-Venanta, w którym przyjmuje się, że o zniszczeniu decyduje największe, spośród trzech, właściwe wydłużenie główne.
Innym kryterium jest kryterium największego naprężenia stycznego, które jak wynika z konstrukcji koła naprężeń Mohra, zależy od różnicy między największym i najmniejszym naprężeniem głównym.
Jednym z powszechnie stosowanych kryteriów jest sformułowane po raz pierwszy przez Hubera kryterium energetyczne. Huber analizując zjawiska fizyczne towarzyszące odkształceniu cial stałych doszedł do wniosku, że za miarę wytężenia materiału w złożonym stanie naprężenia może być uważana ta część energii, która przypada na zmianę postaci ciała, czyli energia odkształcenia postaciowego.
W naszym przypadku wyniki badań zostały opracowane na podstawie dwóch kryteriów, a mianowicie kryterium Coulomba-Mohra oraz Hooke`a Browna.
Dane laboratoryjne:
PIASKOWIEC DROBNOZIARNISTY - szyb Kopernik H=95m
Wytrzymałość na rozciąganie:
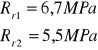
Wytrzymałość na jednoosiowe ściskanie:

Wyniki badań przeprowadzonych w komorze Karmana:
σ3 [MPa] |
σ1 [MPa] |
20 |
185,8 |
40 |
263,4 |
60 |
336,3 |
Z powyższych danych określone zostały następujące parametry kryteriów wytrzymałościowych:
Na podstawie kryterium Couloba-Mohra ![]()
Na podstawie kryterium Hooke`a-Browna ![]()
Kryterium Coulomba Mohra:
W swych podstawowych założeniach w kryterium Mohra zakłada się, że zniszczenie górotworu w złożonym stanie naprężenia zachodzi przez poślizg w płaszczyznach naprężeń stycznych, które zależą od naprężeń normalnych.
Kryterium to wyraża zależność:
![]()
Rysunek 2. Poślizg w płaszczyznach naprężeń stycznych.
Wychodząc z założenia, że podstawowymi parametrami wytrzymałościowymi dla skał jest ich wytrzymałość na ściskanie i rozciąganie, w układzie współrzędnych: ![]()
![]()
wykreśla się okręgi o średnicach odpowiadających wytrzymałościom na rozciąganie i ściskanie. Są to tzw. Koła naprężeń granicznych Mohra. Koła te są miejscem geometrycznym wszystkich punktów odpowiadającym stanom naprężeń wszystkich płaszczyzn przechodzących przez dany punkt.
Punkt styczności kół z obwiednią wskazuje, że badana próbka uległa zniszczeniu.
Obwiednia Mohra w najprostszym przypadku jest linią prostą o równaniu:
![]()
gdzie: ![]()
naprężenia ścinające (styczne)
![]()
naprężenia ściskające (normalne)
![]()
kąt tarcia wewnętrznego
c - kohezja (spójność)
W trójosiowym stanie naprężeń obwiednia Mohra nie jest linią prostą w związku z czym przedstawia się ją w postaci dwóch stycznych, na podstawie których określa się kąt tarcia wewnętrznego oraz spójność tak jak zostało to przedstawione na rysunku poniżej.
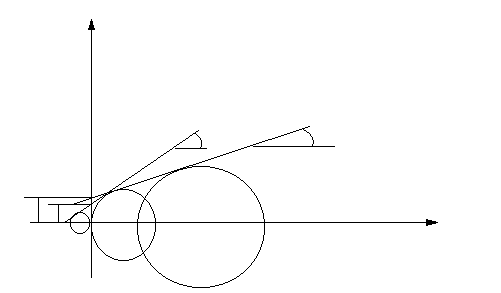
Wykres1. 4 . Sposób określania kohezji i kąta tarcia wewnetrznego na podstawie kół Mohra
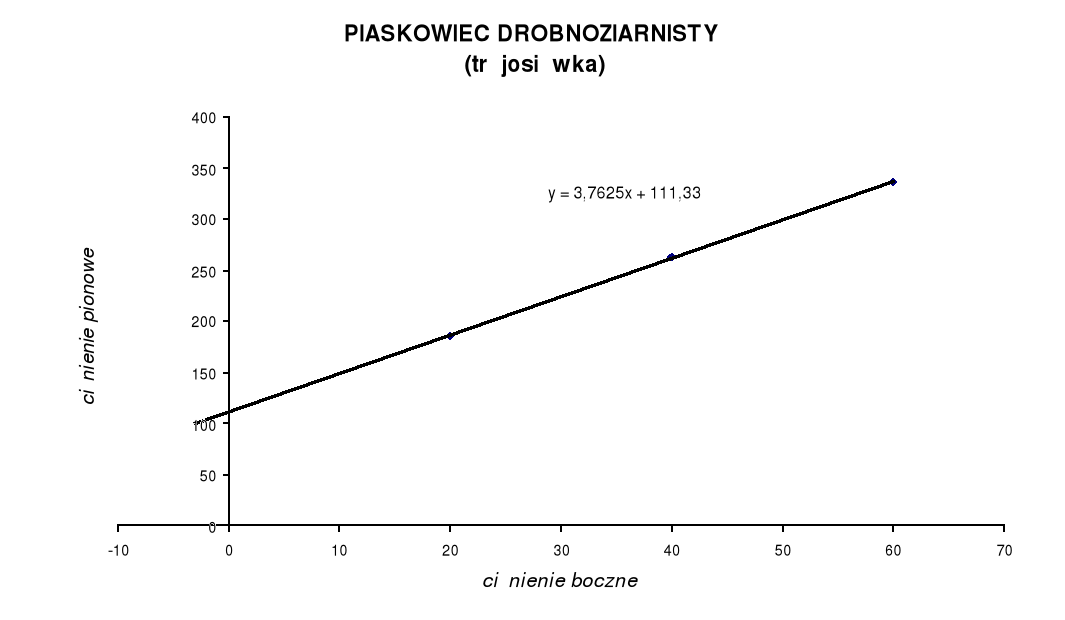
Na potrzeby programu Exel stworzono postać matematyczną kół Mohra (metodą najmniejszych kwadratów) w taki sposób, że zastąpiono je punktami na podstawie których wykreślono dwie proste. Pierwsza prosta została wykonana dla jednoosiowego stanu naprężeń. Do tego celu użyto danych laboratoryjnych uzyskanych z badań na jednoosiowe ściskanie i rozciąganie. Druga prosta wykonana została na podstawie danych z badań w komorze Karmana dla trójosiowego stanu naprężeń.
Równanie prostych przyjęło więc postać:
![]()
co odpowiada matematycznej postaci:
y = ax + b
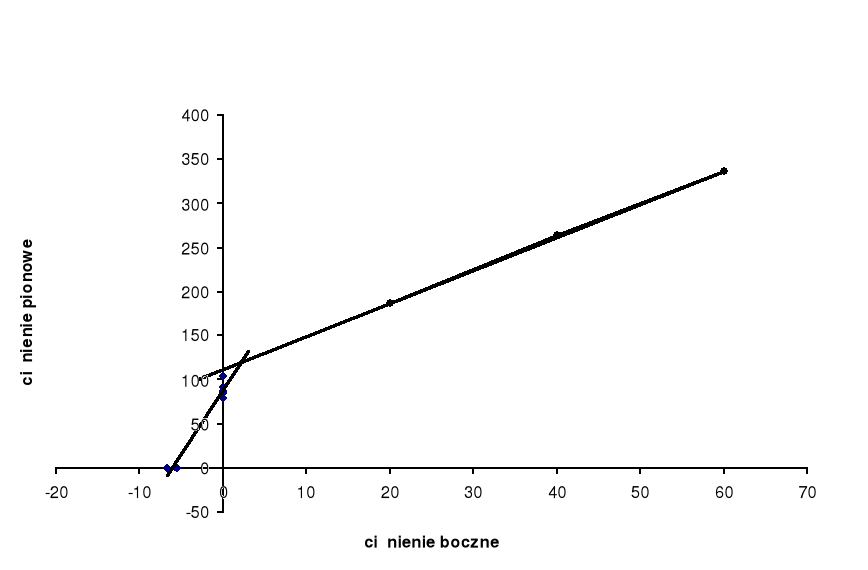
na tej podstawie wykreślono wykresy zależności :
![]()
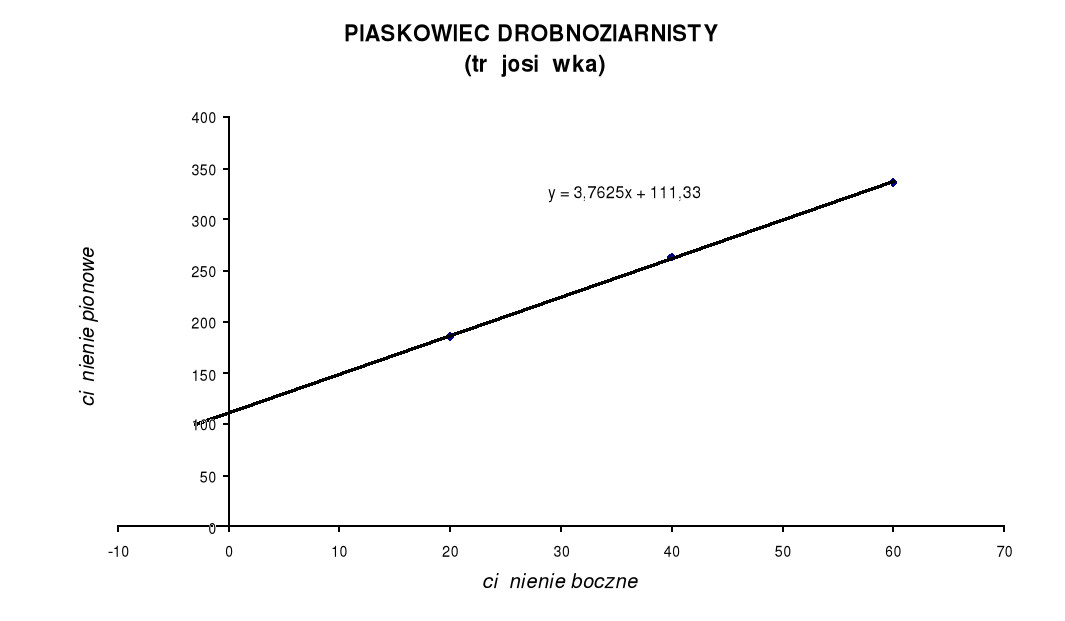
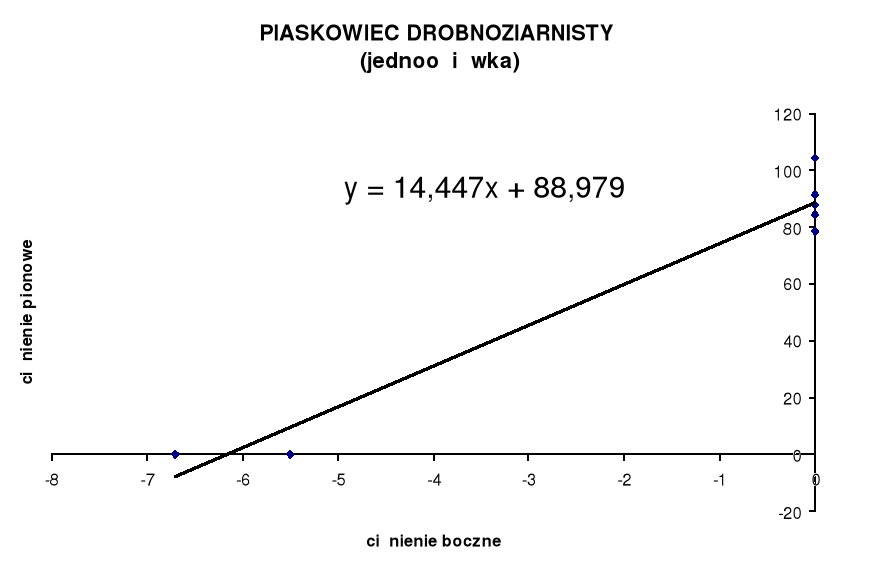
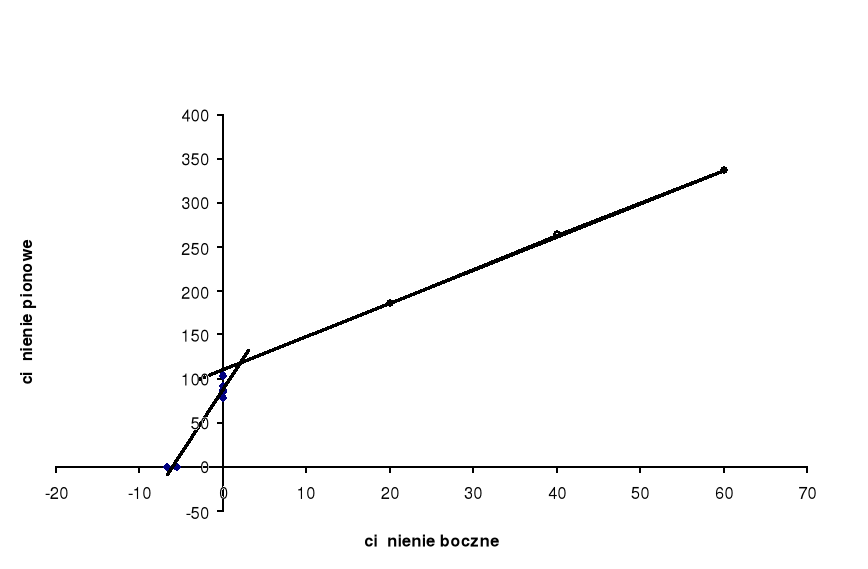
Po uzyskaniu równania prostej wyliczono określone parametry:
![]()
kąt tarcia wewnętrznego,
![]()
spójność
Dla jednoosiowego stanu naprężeń:
Y = 14,447x + 88,979
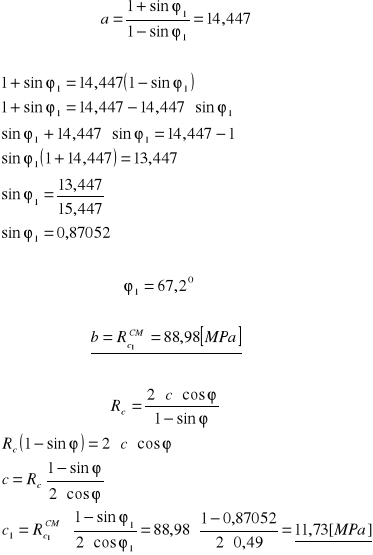
Dla trójosiowego stanu naprężeń :
Y=3,7625x + 111,33
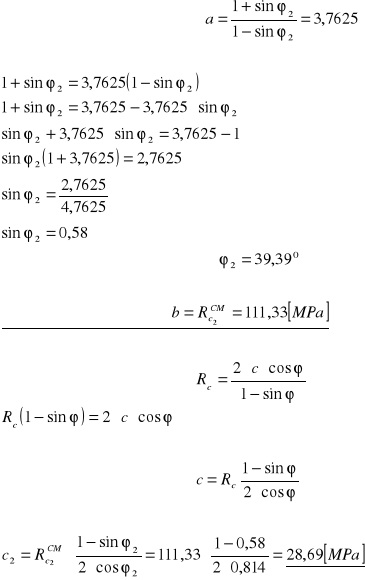
Ostateczne wyniki zebrano w tabeli:
σ3 [MPa] |
σ1 [MPa] |
ϕ1 [°] |
c1 [MPa] |
ϕ2 [°] |
c2 [MPa] |
Rc2CM [MPa] |
20 |
185,8 |
|
|
|
|
|
40 |
263,4 |
67,2 |
11,73 |
39,39 |
28,69 |
111,33 |
60 |
336,3 |
|
|
|
|
|
Kryterium Hooke`a Browna:
Kryterium to zakłada że naprężenie główne ![]()
wyraża się zależnością:
![]()
Po sprowadzeniu tej zależności do postaci równania matematycznego funkcji otrzymano równanie postaci:
![]()
y = ax +b
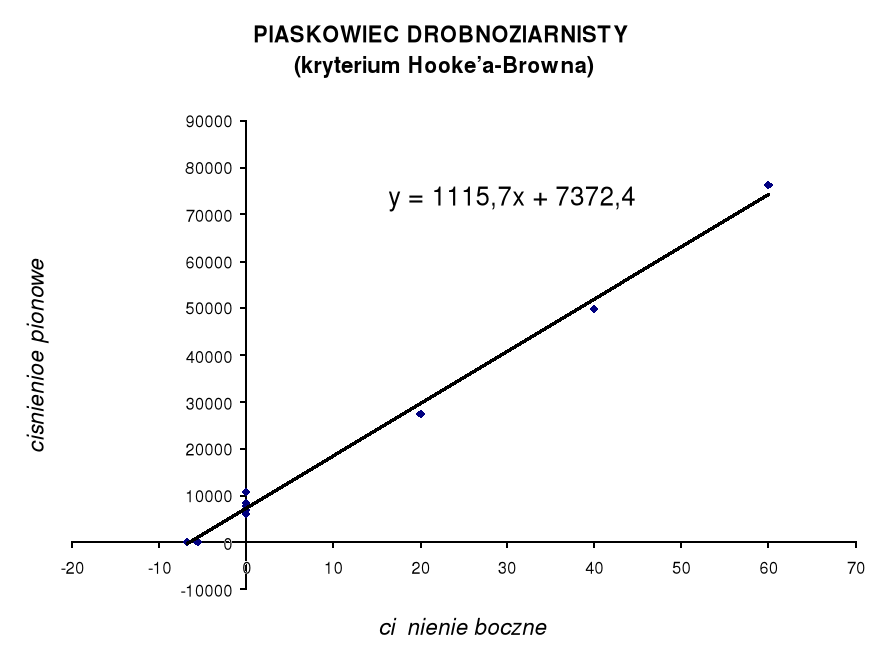
Na jego podstawie i obliczeń zamieszczonych w tabeli poniżej sporządzono wykres zależności:
![]()
|
|
|
-6,7 |
0 |
44,89 |
-5,5 |
0 |
30,25 |
0 |
78,7 |
6193,69 |
0 |
91,5 |
8372,25 |
0 |
87,8 |
7708,84 |
0 |
104,3 |
10878,49 |
0 |
84,3 |
7106,49 |
20 |
185,8 |
27489,64 |
40 |
263,4 |
49907,56 |
60 |
336,3 |
76341,69 |
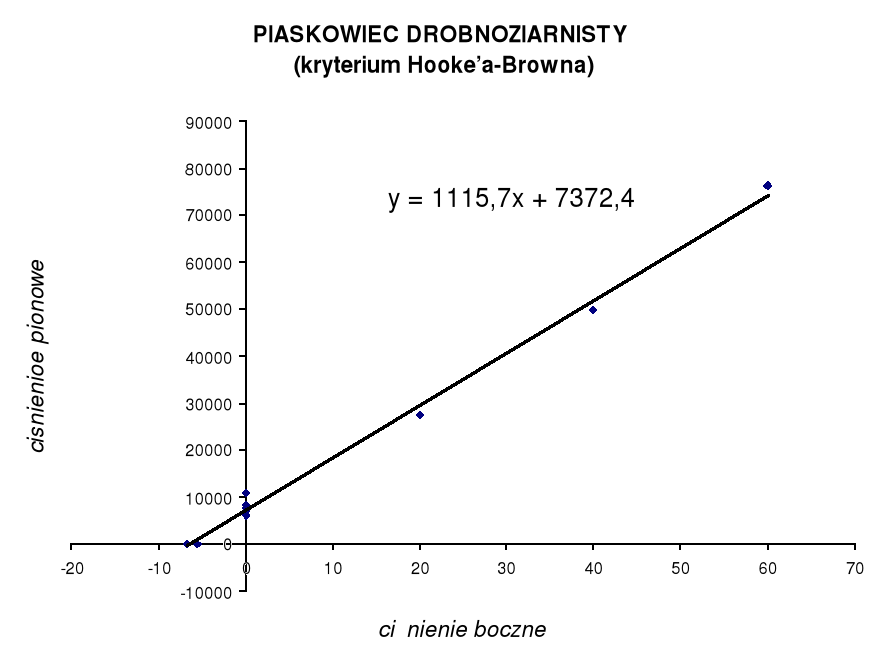
Na podstawie uzyskanego równania:
Y = 1115,7x + 7372,4
Obliczono parametry:
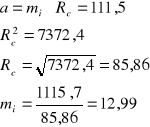
Przykładowe wyniki badań mechanicznych własności skał w trójosiowym stanie naprężeń:
Rodzaj skały |
Naprężenie poziome |
Naprężenie pionowe |
Wytrzymałość na ściskanie |
Kohezja i |
kąt tarcia c, |
wewnętrz ϕ |
nego |
|
σ2 σ3 |
σ1 |
Rc |
w jednoos nie napręż |
iowym sta enia |
w trójosio nie napręż |
wym sta enia |
|
[MPa] |
[MPa] |
[MPa] |
c1 [MPa] |
ϕ1 [°] |
c2 [MPa] |
ϕ2 [°] |
Piaskowiec szary, masywny, silnie zwięzły |
0 20 40 60 |
201,8 326,3 448,5 563,8 |
201,8 |
32 |
67 |
50 |
43 |
Dolomit ciemnoszary, ilasty, masywny, silnie zwięzły |
0 20 40 60 |
265,5 455,3 584,4 751,3 |
265,5 |
36 |
72 |
60 |
49 |
Anhydryt jasnoszary, masywny |
0 20 40 60 |
127,3 228,5 283,4 342,3 |
127,3 |
22 |
64,5 |
40 |
30 |
Wapień szary, zwięzły, pelityczny |
0 20 40 60 |
115,3 205,6 259,0 312,8 |
115,3 |
19 |
65,5 |
46 |
27 |
Wapień szary, ilasty |
0 20 40 60 |
62,3 96,4 126,6 156,4 |
62,3 |
8,5 |
60 |
11 |
28 |
Piaskowiec brunatno - czerwony, kruchy |
0 20 40 60 |
26,8 67,0 90,4 117,5 |
26,8 |
4,5 |
58 |
14 |
24 |
Iłowiec szaroseledynowy, zaburzony |
0 20 40 60 |
24,2 62,2 93,6 119,2 |
24,2 |
4 |
57 |
15 |
24,5 |
1
1
Wyszukiwarka