 | Pobierz cały dokument wydymala.opracowanie.pytan.wytrzymalosc.doc Rozmiar 858 KB |
1. Modelowanie w wytrzymałości materiałów
Modelowanie jest to czynność polegająca na przejściu od obiektu rzeczywistego poprzez model fizyczny, do modelu matematycznego. Model matematyczny jest to matematyczny opis zjawisk zachodzących w modelu fizycznym, podany w formie usystematyzowanych wzorów lub równań - algorytm. Do sformułowania kryteriów niezawodności wytrzymałościowej istnieje potrzeba tworzenia modeli: -modele materiału; -model postaci (kształtu); -model obciążenia; -modele złomu.
2. Charakterystyki geometryczne przekroju poprzecznego pręta.
Momenty bezwładności przekroju względem osi y i z:
![]()
![]()
Moment dewiacji przekroju pręta w płaszczyźnie yz:
![]()
Biegunowy moment przekroju względem punktu O:
![]()
Momenty statyczne przekroju względem osi y i z:
![]()
![]()
![]()
- współrzędne środka geometrycznego przekroju S (zwanego środkiem ciężkości).
3. Charakterystyki geometryczne przekroju poprzecznego pręta w układzie współrzędnych przesuniętym równolegle.
Sxy - układ osi centralnych
Momenty geometryczne przekroju w układzie współrzędnych Oηζ przesuniętym równolegle (twierdzenie Steinera)
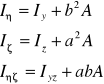
4. Charakterystyki geometryczne przekroju poprzecznego pręta w układzie współrzędnych obróconym.
![]()
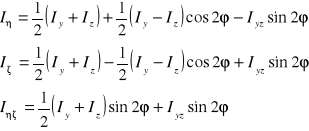
5. Główne momenty bezwładności i główne osie bezwładności przekroju pręta.
↑ Osie η=1, ζ=2 będą głównymi centralnymi osiami bezwładności przekroju.
Główne centralne momenty bezwładności przekroju
![]()
Inny sposób. Jeżeli w układzie prostokątnym Syz momenty bezwładności przekroju wynoszą Iy, Iz, zaś moment dewiacji Iyz, to główne centralne momenty bezwładności I1, I2 są wartościami własnymi tensora momentów geometrycznych
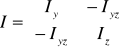
6. Ściskanie/rozciąganie pręta prostego. Warunki równowagi, warunki geometryczne i zależności fizyczne.
Warunki równowagi:
Warunki geometryczne:
Przemieszczenie osiowe elementu pręta dx: -górnego końca u; -dolnego końca u+du,
Długość elementu po odkształceniu dx+du,
Odkształcenie względne:
![]()
,
Przemieszczenie dolnego końca pręta:
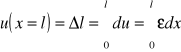
Przypadek szczególny (ε=const)
![]()
Zależności fizyczne:
W zakresie odkształceń liniowych obowiązuje prawo Hooke'a, które możemy zapisać w następującej postaci:
![]()
E - moduł sprężystości liniowej, moduł Younga, A - pole przekroju poprzecznego ciała odkształcalnego
Przyjmując na powierzchni przekroju poprzecznego równomierny rozkład naprężeń, możemy je wyrazić wzorem:
![]()
naprężenia ściskające bądź rozciągające
Prawo sprężystości liniowej (przekształcone prawo Hooke'a) w jednoosiowym stanie naprężeń:
![]()
 | Pobierz cały dokument wydymala.opracowanie.pytan.wytrzymalosc.doc rozmiar 858 KB |