Gliwice, 12.11.2005
OBWIEDNIA MOMENTÓW ZGINAJĄCYCH
BELKA WOLNOPODPARTA ZE WSPORNIKAMI
________________________________________________________________________________
TEMAT:
Grupa obciążeń (rys.1) porusza się po konstrukcji (w przedziale oznaczonym linią przerywaną). Ciężar własny ustroju g=10 kN/m (g=γ⋅A, gdzie: γ - ciężar objętościowy materiału, A - pole przekroju poprzecznego pręta).
Wyznaczamy obwiednię momentu zginającego w belce -rys.2.
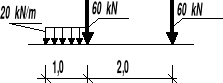
Rys.1

Rys.2
________________________________________________________________________________
ROZWIĄZANIE:
Ustalamy położenia przekrojów, dobranych dostatecznie gęsto, aby zapewnić niezbędną dokładność obliczeń (rys.3).

Rys.3.
Dla kolejnych przekrojów sporządzamy linie wpływu analizowanej wielkości wewnętrznej (w naszym przypadku momentu zginającego). Następnie wykorzystując linie wpływu znajdujemy wartości ekstremalne (maksimum i minimum w sensie liczbowym) tej wielkości, pochodzące od danej grupy obciążeń.
Wielkości ekstremalne wyznaczamy tu metodą prób, co pokazano przykładowo na rys.4, poszukując maksymalnego momentu zginającego w przekroju 8 belki z rys.3.
Rozpatrzono trzy ustawienia grupy obciążeń nad linią wpływu momentu w przekroju 8 (M8).
Dla ustawienia pierwszego U1 mamy:
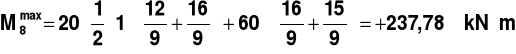
,
Dla ustawienia drugiego U2:
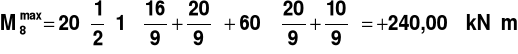
,
Dla ustawienia trzeciego U3:
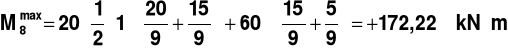
,

Rys.4.
Najbardziej niekorzystnym ustawieniem jest ustawienie U2, a wartość maksymalna momentu zginającego wynosi: M=240,00 kN⋅m
________________________________________________________________________________
Rozpatrzymy teraz kolejne przekroje belki.
PRZEKRÓJ 1

Rys.5.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 2

Rys.6.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 3

Rys.7.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 4

Rys.8.
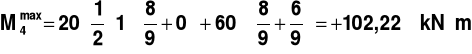
,
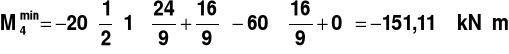
________________________________________________________________________________
PRZEKRÓJ 5

Rys.9.
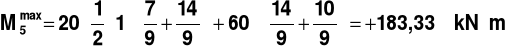
,
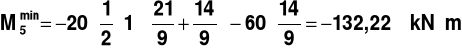
________________________________________________________________________________
PRZEKRÓJ 6

Rys.10.
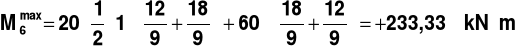
,
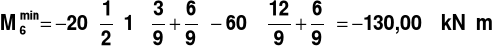
________________________________________________________________________________
PRZEKRÓJ 7

Rys.11.
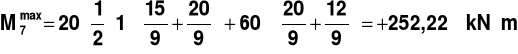
,
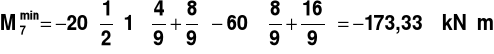
________________________________________________________________________________
PRZEKRÓJ 8

Rys.12.
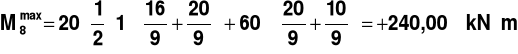
,
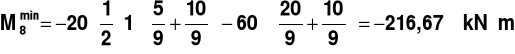
________________________________________________________________________________
PRZEKRÓJ 9

Rys.13.
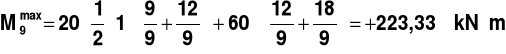
,
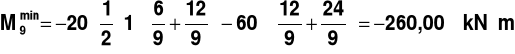
________________________________________________________________________________
PRZEKRÓJ 10

Rys.14.
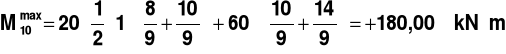
,
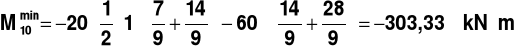
________________________________________________________________________________
PRZEKRÓJ 11

Rys.15.
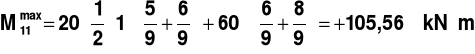
,
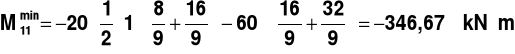
________________________________________________________________________________
PRZEKRÓJ 12

Rys.16.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 13

Rys.17.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 14

Rys.18.
![]()
![]()
________________________________________________________________________________
PRZEKRÓJ 15

Rys.19.
![]()
![]()
________________________________________________________________________________
________________________________________________________________________________
Obliczamy teraz wartości momentów zginających w kolejnych przekrojach belki, pochodzące od ciężaru własnego konstrukcji - rys.20 i tablica 1.
Następnie sumujemy wartości momentów zginających od ciężaru własnego z wartościami ekstremalnymi momentów od obciążenia ruchomego (otrzymanymi na podstawie linii wpływu) - tablica 1 oraz rys.21.
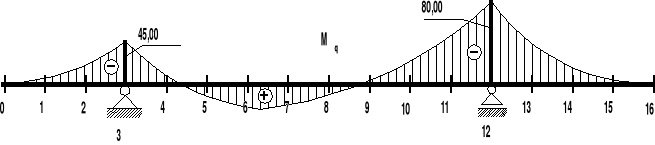
Rys.20.
Tablica 1
Przekrój |
Mq |
Mmax |
Mmin |
Mmax+q |
Mmin+q |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-5,00 |
0 |
-10,00 |
-5,00 |
-15,00 |
2 |
-20,00 |
0 |
-90,00 |
-20,00 |
-110,00 |
3 |
-45,00 |
0 |
-230,00 |
-45,00 |
-275,00 |
4 |
-8,89 |
+102,22 |
-151,11 |
+93,33 |
-160,00 |
5 |
+17,22 |
+183,33 |
-132,22 |
+200,55 |
-115,00 |
6 |
+33,33 |
+233,33 |
-130,00 |
+266,66 |
-96,67 |
7 |
+39,44 |
+252,22 |
-173,33 |
+291,66 |
-133,89 |
8 |
+35,56 |
+240,00 |
-216,67 |
+275,56 |
-181,11 |
9 |
+21,67 |
+223,33 |
-260,00 |
+245,00 |
-238,33 |
10 |
-2,22 |
+180,00 |
-303,00 |
+177,78 |
-305,22 |
11 |
-36,11 |
+105,56 |
-346,67 |
+69,45 |
-382,78 |
12 |
-80,00 |
0 |
-390,00 |
-80,00 |
-470,00- |
13 |
-45,00 |
0 |
-250,00 |
-45,00 |
295,00 |
14 |
-20,00 |
0 |
-120,00 |
-20,00 |
-140,00 |
15 |
-5,00 |
0 |
-60,00 |
-5,00 |
-65,00 |
16 |
0 |
0 |
0 |
0 |
0 |
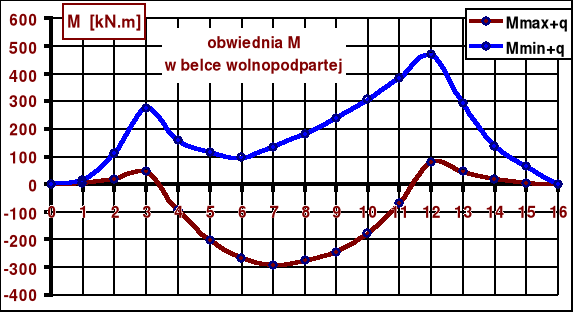
Rys.21.
1
Wyszukiwarka