Poz. 3 Podciąg

3.1 Schemat statyczny

3.2 Zestawienie obciążeń

- obciążenia stałe:

• od reakcji belek stropowych:

• ciężar własny podciągu:

Razem: g_k=21,655 kN/m

- obciążenia zmienne:

• użytkowe z Poz. 2.2

q_k= 38,5 kN/m

3.3 Obliczenia statyczne

Wyznaczamy momenty zginające: M=α∙1,35∙g∙l²+β∙1,5∙q∙l²

Przęsło A-B oraz B-A'

M_0,1^max=0,0325∙1,35∙21,655∙10²+0,03875∙1,5∙38,5∙10²= 318,793 kNm

M_0,1^min=0,0325∙1,35∙21,655∙10²-0,00625∙1,5∙38,5∙10²= 58,918 kNm

M_0,2^max=0,0505∙1,35∙21,655∙10²+0,06750∙1,5∙38,5∙10²= 537,445 kNm

M_0,2^min=0,0505∙1,35∙21,655∙10²-0,01250∙1,5∙38,5∙10²= 75,445 kNm

M_0,3^max=0,0675∙1,35∙21,655∙10²+0,08625∙1,5∙38,5∙10²= 695,425 kNm

M_0,3^min=0,0675∙1,35∙21,655∙10²-0,01875∙1,5∙38,5∙10²= 89,050 kNm

M_0,4^max=0,0700∙1,35∙21,655∙10²+0,09500∙1,5∙38,5∙10²= 753,265 kNm

M_0,4^min=0,0700∙1,35∙21,655∙10²-0,02500∙1,5∙38,5∙10²= 60,264 kNm

M_0,5^max=0,0625∙1,35∙21,655∙10²+0,09375∙1,5∙38,5∙10²= 724,120 kNm

M_0,5^min=0,0625∙1,35∙21,655∙10²-0,03125∙1,5∙38,5∙10²= 2,245 kNm

M_0,6^max=0,0450∙1,35∙21,655∙10²+0,08250∙1,5∙38,5∙10²= 607,992 kNm

M_0,6^min=0,0450∙1,35∙21,655∙10²-0,03750∙1,5∙38,5∙10²= -85,008 kNm

M_0,7^max=0,0175∙1,35∙21,655∙10²+0,06125∙1,5∙38,5∙10²= 404,879 kNm

M_0,7^min=0,0175∙1,35∙21,655∙10²-0,04375∙1,5∙38,5∙10²= -201,496 kNm

M_0,8^max=-0,0200∙1,35∙21,655∙10²+0,03000∙1,5∙38,5∙10²= 114,782 kNm

M_0,8^min=-0,0200∙1,35∙21,655∙10²-0,05000∙1,5∙38,5∙10²= -347,219 kNm

M_0,9^max=-0,0675∙1,35∙21,655∙10²+0,00611∙1,5∙38,5∙10²= -162,046 kNm

M_0,9^min=-0,0675∙1,35∙21,655∙10²-0,07361∙1,5∙38,5∙10²= -622,429 kNm

M_1,0^max=-0,1250∙1,35∙21,655∙10²+0,0 ∙1,5∙38,5∙10²= -365,428 kNm

M_1,0^min=-0,1250∙1,35∙21,655∙10²-0,12500 ∙1,5∙38,5∙10²= -1087,303 kNm

Wyznaczenie sił poprzecznych: V=α∙1,35∙g∙l+β∙1,5∙q∙l

Przęsło A-B oraz B-A'

V_0,0^max=0,375∙1,35∙21.655∙10+0,4375∙1,5∙38,5∙10= 362,285 kN

V_0,0^min=0,375∙1,35∙21.655∙10-0,0625∙1,5∙38,5∙10= 73,535 kN

V_0,1^max=0,275∙1,35∙21.655∙10+0,3437∙1,5∙38,5∙10= 278,881 kN

V_0,1^min=0,275∙1,35∙21.655∙10-0,0687∙1,5∙38,5∙10= 40,720 kN

V_0,2^max=0,175∙1,35∙21.655∙10+0,2624∙1,5∙38,5∙10= 202,696 kN

V_0,2^min=0,175∙1,35∙21.655∙10-0,0874∙1,5∙38,5∙10= 0,686 kN

V_0,3^max=0,075∙1,35∙21.655∙10+0,1932∙1,5∙38,5∙10= 133,499 kN

V_0,3^min=0,075∙1,35∙21.655∙10-0,1182∙1,5∙38,5∙10= -46,335 kN

V_0,4 ^max=-0,025∙1,35∙21.655∙10+0,1359∙1,5∙38,5∙10= 71,174 kN

V_0,4 ^min=-0,025∙1,35∙21.655∙10-0,1609∙1,5∙38,5∙10= -129,463 kN

V_0,5 ^max=-0,125∙1,35∙21.655∙10+0,0898∙1,5∙38,5∙10= 15,317 kN

V_0,5 ^min=-0,125∙1,35∙21.655∙10-0,2148∙1,5∙38,5∙10= -160,590 kN

V_0,6 ^max=-0,225∙1,35∙21.655∙10+0,0544∙1,5∙38,5∙10= -34,361 kN

V_0,6 ^min=-0,225∙1,35∙21.655∙10-0,2794∙1,5∙38,5∙10= -227,131 kN

V_0,7 ^max=-0,325∙1,35∙21.655∙10+0,0287∙1,5∙38,5∙10= -78,437 kN

V_0,7 ^min=-0,325∙1,35∙21.655∙10-0,3537∙1,5∙38,5∙10= -299,273 kN

V_0,8 ^max=-0,425∙1,35∙21.655∙10+0,0119∙1,5∙38,5∙10= -117,373 kN

V_0,8 ^min=-0,425∙1,35∙21.655∙10-0,4369∙1,5∙38,5∙10= -376,555 kN

V_0,9 ^max=-0,525∙1,35∙21.655∙10+0,0027∙1,5∙38,5∙10= -151,921 kN

V_0,9 ^min=-0,525∙1,35∙21.655∙10-0,5277∙1,5∙38,5∙10= -458,227 kN

V_1,0 ^max=-0,625∙1,35∙21.655∙10+0,0∙1,5∙38,5∙10= -182,714 kN

V_1,0 ^min=-0,625∙1,35∙21.655∙10-0,6250∙1,5∙38,5∙10= -543,651 kN

3.4 Kształtowanie podłużne oraz dobór przekrojów poprzecznych blachownic.

Wstępna wysokość blachownicy ciągłej:

Przyjęto stałe wymiary środnika blachownicy:

- grubość środnika

t_w= 7+ 3h_w= 7+ 3∙ 0,6= 8,8≈ 9,0mm

- wysokość środnika

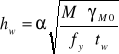
gdzie:

M=753,265 kNm= 753265000 Nmm

γ_M0= 1,0

f_y= 275 N/mm²

t_w= 9,0 mm

α= 1,1

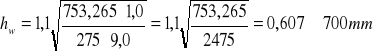
Moment bezwładności środnika blachownicy:

gdzie:

t_w= 9,0 mm

h_w= 700 mm

Grubość pasa:

Przekrój I

M_{0,2 Ed}= 537,445 kNm= 537445000 Nmm

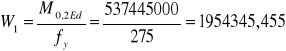
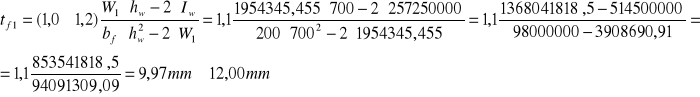
Przekrój II

M_{0,4 Ed}= 753,265 kNm= 753265000 Nmm

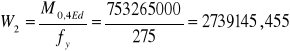
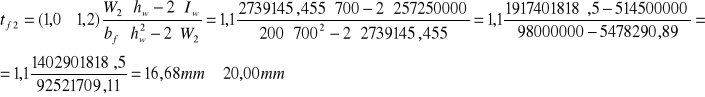
Przekrój III

M_{1,0 Ed}= 1087,303 kNm= 1087303000 Nmm

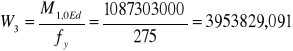
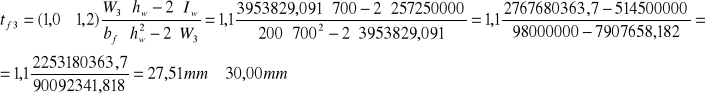
3.5 Sprawdzenie stanu granicznego nośności.

3.5.1 Podpora A (przekrój nr IV, V_Ed=362 kN, M_Ed=0 kNm)

Stal gatunku S275, t_f=12,0 < 40,0 mm -> f_y= 275 N/mm²

f_u= 430 N/mm²

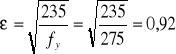
Charakterystyka przekroju:

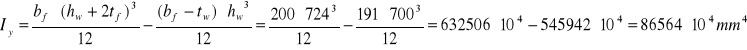
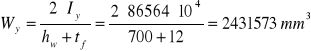
Sprawdzenie klasy przekroju:

- Pas

Smukłość pasa

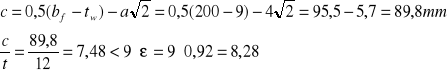
Pas spełnia warunek klasy 1.

- Środnik

Smukłość środnika

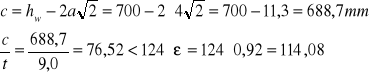
Środnik spełnia warunek klasy 3.

Efekt szerokiego pasa:

Efekt szerokiego pasa nie występuje.

Nośność przy naprężeniach stycznych:

Współczynnik niestateczności

Określenie nośności obliczeniowej środnika przy ścinaniu V_bw,Rd

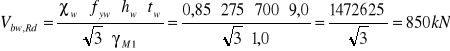
Określenie udziału pasów w nośności obliczeniowej przy ścinaniu.

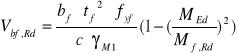
M_Ed= 0;

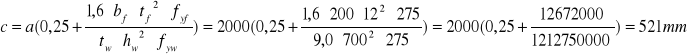
Wyznaczenie nośności obliczeniowej środnika przy uplastycznieniu.

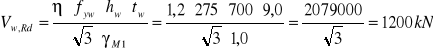
Sprawdzenie nośności obliczeniowej przekroju przy ścinaniu blachownicy.

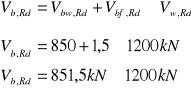
Obliczeniowa siła poprzeczna.

V_Ed= 362 kN

Sprawdzenie warunku nośności przekroju przy ścinaniu.

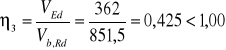
Odp. Warunek jest spełniony.

Interakcja siły poprzecznej i momentu zginającego:

M_Ed= 0 kNm

V_Ed= 362 kN

Nie jest wymagane uwzględnienie interakcji, gdyż redukcja nośności przekroju ze względu na ścinanie przy obciążeniu momentem zginającym i siłą poprzeczną nie jest wymagane.

3.5.2 Przęsło A-B (przekrój nr I, V_Ed= 362 kN, M_Ed= 537 kNm)

Stal gatunku S275, t_f=12,0 < 40,0 mm -> f_y= 275 N/mm²

f_u= 430 N/mm²

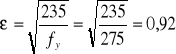
Charakterystyka przekroju:

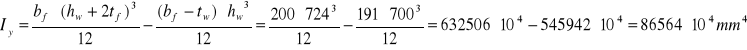
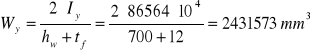
Sprawdzenie klasy przekroju:

- Pas

Smukłość pasa

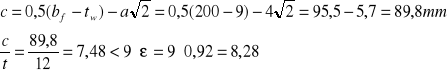
Pas spełnia warunek klasy 1.

- Środnik

Smukłość środnika

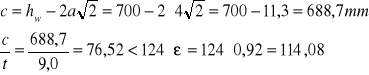
Środnik spełnia warunek klasy 3.

Efekt szerokiego pasa:

Efekt szerokiego pasa nie występuje.

Zwichrzenie belki:

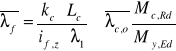
gdzie:

L_c= 2000mm

k_c= 1,0

Ψ_c= 1,0

Promień bezwładności przekroju pasa zastępczego.

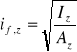
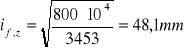
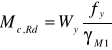
gdzie:

W_y= 2431573 mm³

f_y= 275 N/mm²

γ_M1= 1,0

Odp. Zwichrzenie nie wystąpi

Warunek nośności na zginanie:

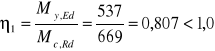
Odp. Warunek jest spełniony.

Nośność przy naprężeniach stycznych:

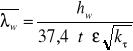
gdyż

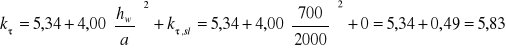
Współczynnik niestateczności

Wyznaczenie nośności obliczeniowej środnika przy uplastycznieniu.

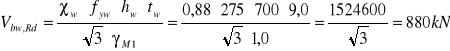
Pominięto udział pasów w nośności obliczeniowej przy ścinaniu.

Obliczeniowa siła poprzeczna.

V_Ed= 362 kN= 362∙10³ N

Sprawdzenie warunku nośności przekroju przy ścinaniu.

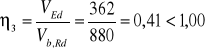
Odp. Warunek jest spełniony.

Interakcja siły poprzecznej i momentu zginającego:

M_Ed= 537 kNm

V_Ed= 362 kN

Nie jest wymagane uwzględnienie interakcji, gdyż redukcja nośności przekroju ze względu na ścinanie przy obciążeniu momentem zginającym i siłą poprzeczną nie jest wymagane.

3.5.3 Przęsło A-B (przekrój nr II, V_Ed=0 kN, M_Ed= 753 kNm)

Stal gatunku S275, t_f=12,0 < 40,0 mm -> f_y= 275 N/mm²

f_u= 430 N/mm²

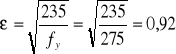
Charakterystyka przekroju:

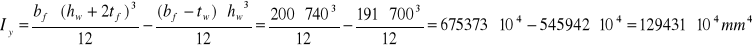
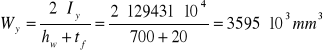
Sprawdzenie klasy przekroju:

- Pas

Smukłość pasa

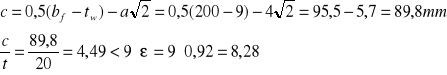
Pas spełnia warunek klasy 1.

- Środnik

Smukłość środnika

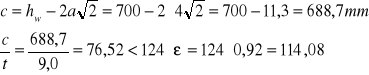
Środnik spełnia warunek klasy 3.

Efekt szerokiego pasa:

Efekt szerokiego pasa nie występuje.

Zwichrzenie belki:

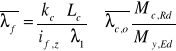
gdzie:

L_c= 2000mm

k_c= 1,0

Ψ_c= 1,0

Promień bezwładności przekroju pasa zastępczego.

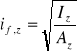
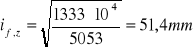
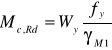
gdzie:

W_y= 3595∙10³ mm³

f_y= 275 N/mm²

γ_M1= 1,0

Odp. Zwichrzenie nie wystąpi

Warunek nośności na zginanie:

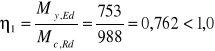
Odp. Warunek jest spełniony.

3.5.4 Przęsło A-B (przekrój nr V, V_Ed= 376 kN, M_Ed= 405 kNm)

Stal gatunku S275, t_f=12,0 < 40,0 mm -> f_y= 275 N/mm²

f_u= 430 N/mm²

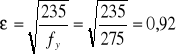
Charakterystyka przekroju:

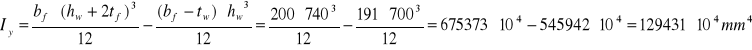
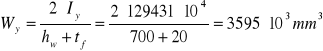
Sprawdzenie klasy przekroju:

- Pas

Smukłość pasa

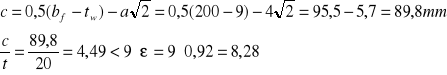
Pas spełnia warunek klasy 1.

- Środnik

Smukłość środnika

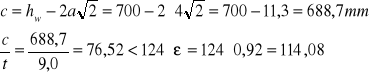
Środnik spełnia warunek klasy 3.

Efekt szerokiego pasa:

Efekt szerokiego pasa nie występuje.

Zwichrzenie belki:

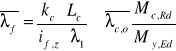
gdzie:

L_c= 2000mm

k_c= 1,0

Ψ_c= 1,0

Promień bezwładności przekroju pasa zastępczego.

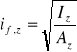
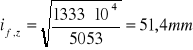
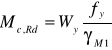
gdzie:

W_y= 3595∙10³ mm³

f_y= 275 N/mm²

γ_M1= 1,0

Odp. Zwichrzenie nie wystąpi

Warunek nośności na zginanie:

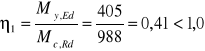
Odp. Warunek jest spełniony.

Nośność przy naprężeniach stycznych:

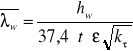
gdyż

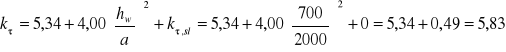
Współczynnik niestateczności

Wyznaczenie nośności obliczeniowej środnika przy uplastycznieniu.

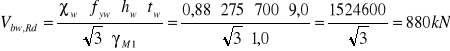
Pominięto udział pasów w nośności obliczeniowej przy ścinaniu.

Obliczeniowa siła poprzeczna.

V_Ed= 376 kN= 376∙10³ N

Sprawdzenie warunku nośności przekroju przy ścinaniu.

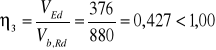
Odp. Warunek jest spełniony.

Interakcja siły poprzecznej i momentu zginającego:

M_Ed= 405 kNm

V_Ed= 376 kN

Nie jest wymagane uwzględnienie interakcji, gdyż redukcja nośności przekroju ze względu na ścinanie przy obciążeniu momentem zginającym i siłą poprzeczną nie jest wymagane.

3.5.5 Podpora B (przekrój nr III, V_Ed= 543 kN, M_Ed= 1087 kNm)

Stal gatunku S275, t_f=12,0 < 40,0 mm -> f_y= 275 N/mm²

f_u= 430 N/mm²

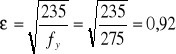
Charakterystyka przekroju:

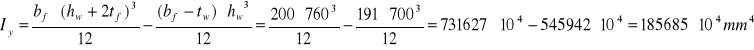
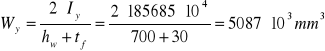
Sprawdzenie klasy przekroju:

- Pas

Smukłość pasa

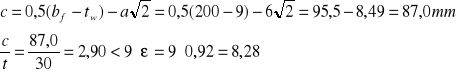
Pas spełnia warunek klasy 1.

- Środnik

Smukłość środnika

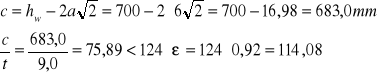
Środnik spełnia warunek klasy 3.

Efekt szerokiego pasa:

- Przęsło:

- Podpora:

Na całej długości blachownicy efekt szerokiego pasa nie występuje.

Zwichrzenie belki:

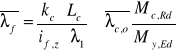
gdzie:

L_c= 4500mm

k_c= 1,0

Ψ_c= 1,0

Promień bezwładności przekroju pasa zastępczego.

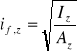
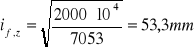
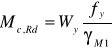
gdzie:

W_y= 5087∙10³ mm³

f_y= 275 N/mm²

γ_M1= 1,0

Odp. Zwichrzenie wystąpi

W celu uniknięcia zwichrzenia zastosujemy zastrzały, sprawdzamy wystąpienie zwichrzenia:

L_c=a = 2000mm

Odp. Zwichrzenie nie wystąpi

Warunek nośności na zginanie:

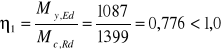
Odp. Warunek jest spełniony.

Nośność przy naprężeniach stycznych:

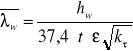
gdyż

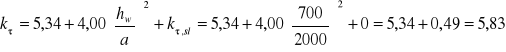
Współczynnik niestateczności

Wyznaczenie nośności obliczeniowej środnika przy uplastycznieniu.

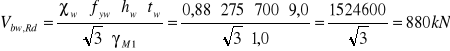
Pominięto udział pasów w nośności obliczeniowej przy ścinaniu.

Obliczeniowa siła poprzeczna.

V_Ed= 543 kN= 543∙10³ N

Sprawdzenie warunku nośności przekroju przy ścinaniu.

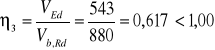
Odp. Warunek jest spełniony.

Interakcja siły poprzecznej i momentu zginającego:

M_Ed= 1087 kNm

V_Ed= 543 kN

Należy uwzględnić interakcję, sprawdzając warunek nośności.

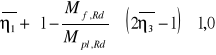
lecz:

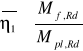
Obliczeniowa nośność przy zginaniu przekroju złożonego wyłącznie z efektywnych części pasów.

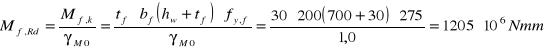
Obliczeniowa nośność plastyczna przy zginaniu przekroju złożonego z efektywnych części pasów oraz w pełni efektywnego środnika.

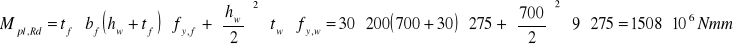
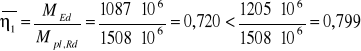
Przyjęto:

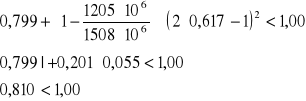
Odp. Warunek jest spełniony.

3.6 Projektowanie żeber usztywniających.

3.6.1 Żebro podporowe (podpora A, przekrój nr IV, V_Ed= 362 kN, M_Ed= 0 kNm)

Żebro podporowe o wymiarach: 12x90 mm

Część współpracująca środnika o szerokości:

b_ws=15∙Ԑ∙t_w

gdzie:

Ԑ= 0,92

t_w= 9,0 mm

b_ws=15∙0,92∙9,0= 124,2 mm

Pole powierzchni:

A_st= 2b_s∙t_s+(30∙Ԑ∙t_w+ t_s)t_w

gdzie:

b_s= 90mm

t_s= 12 mm

t_w= 9 mm

A_st= 2∙90∙12+(30∙0,92∙9+ 12)9=2160+2343,6= 4504 mm²

Moment bezwładności względem osi y.

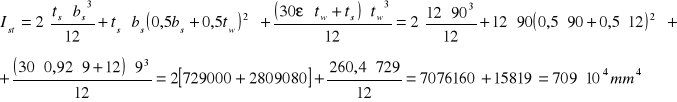
Promień bezwładności.

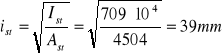
Sprawdzenie klasy przekroju żebra.

Smukłość żebra.

Przekrój jest klasy 3.

Sprawdzenie stateczności żebra ze względu na wyboczenie skrętne.

Rozpatrzono tylko jedną blachę żebra.

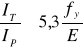
Moment bezwładności przekroju żebra przy skręcaniu swobodnym.

Biegunowy moment bezwładności przekroju żebra względem punktu styczności ze ścianką.

Nie wystąpi skrętna utrata stateczności żeber.

Nośność i stateczność żebra na ściskanie.

Smukłość względna
przy wyboczeniu giętym.

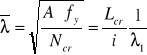
L_cr= 0,75h_w=0,75∙700= 525 mm

Współczynnik wyboczeniowy X=1,0, warunek stateczności sprawdza się do warunku nośności przekroju.

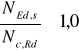
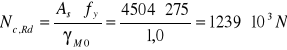
Odp. Warunek spełniony.

Sprawdzenie docisku żebra do pasa.

Powierzchnia docisku:

Naprężenia dociskowe:

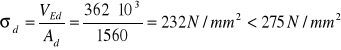
3.6.2 Żebro pośrednie (przęsło A-B, przekrój nr I, V_Ed= 362 kN, M_Ed= 537 kNm)

Założono zastosowanie sztywnych żeber pośrednich dwustronnych z blachy12x90 mm.

Część współpracująca środnika o szerokości:

b_ws=15∙Ԑ∙t_w

gdzie:

Ԑ= 0,92

t_w= 9,0 mm

b_ws=15∙0,92∙9,0= 124,2 mm

Pole powierzchni:

A_st= 2b_s∙t_s+(30∙Ԑ∙t_w+ t_s)t_w

gdzie:

b_s= 90mm

t_s= 12 mm

t_w= 9 mm

A_st= 2∙90∙12+(30∙0,92∙9+ 12)9=2160+2343,6= 4504 mm²

Moment bezwładności względem osi y.

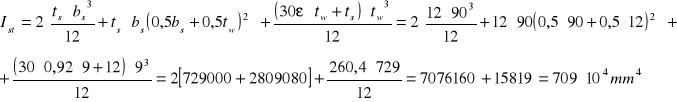
Promień bezwładności.

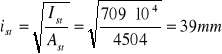
Przyjęte żebro jest sztywnym żebrem pośrednim.

Sprawdzenie klasy przekroju żebra.

Smukłość żebra.

Przekrój jest klasy 3.

Stateczność żebra ze względu na wyboczenie skrętne.

Rozpatrzono tylko jedną blachę żebra.

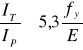
Moment bezwładności przekroju żebra przy skręcaniu swobodnym.

Biegunowy moment bezwładności przekroju żebra względem punktu styczności ze ścianką.

Nie wystąpi skrętna utrata stateczności żeber.

Nośność i stateczność żebra na ściskanie.

Smukłość względna
przy wyboczeniu giętym.

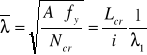
L_cr= 1,0h_w=1,0∙700= 700 mm

Współczynnik wyboczeniowy X=0,99, warunek stateczności sprawdza się do warunku nośności przekroju.

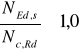
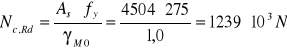
Odp. Warunek spełniony.

Sprawdzenie docisku żebra do pasa.

Powierzchnia docisku:

Naprężenia dociskowe:

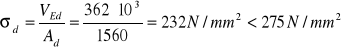
3.7 Projektowanie połączeń i styków.

3.7.1 Połączenie pasa ze środnikiem

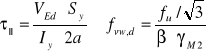
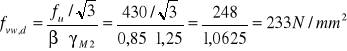
Przekrój I

Przekrój II

Przekrój III

3.7.2 Połączenie żebra ze środnikiem

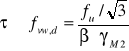
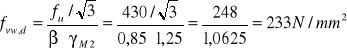
Przekrój I

a= 4mm

e= 45mm

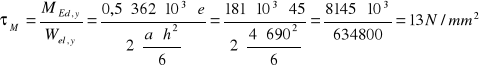
Podpora B

a= 6mm

e= 45mm

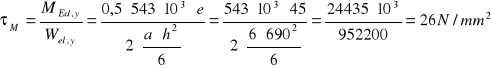
3.7.3 Styk montażowy

Śruby M16 klasy 5.6 -> f_ub= 500 N/mm²

f_yb= 300 N/mm²

A_S= 201 mm²

d= 16mm

d₀= 16+2= 18mm

Stal S275 -> f_y= 275 N/mm²

f_u= 430 N/mm²

Minimalne skrajne odległości

e₁= 1,2d₀= 1,2∙18= 21,6 mm

e₂= 1,2d₀= 1,2∙18= 21,6 mm

p₁= 2,2d₀= 2,2∙18= 39,6 mm

p₂= 2,4d₀= 2,4∙18= 43,2 mm

Przyjęte odległości przy połączeniu przykładek na środniku

e₁= 50 mm

e₂= 50 mm

p₁= 125 mm

p₂= 120 mm

Przyjęte odległości przy połączeniu nakładek na pasach podciągu

e₁= 50 mm

e₂= 50 mm

p₁= 100 mm

p₂= 120 mm

Nakładki

M= 404 kNm

V= 299 kN

e= 120mm

I_p= 15,340∙10⁸mm⁴

I_n= 6,721∙10⁸mm⁴

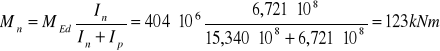
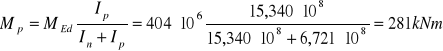
Nośność śruby na ścinanie wynosi:

Płaszczyzna ścinania nie przechodzi przez gwintowaną część śruby: α_v= 0,6

Nośność śruby na docisk do pasa podciągu:

-Śruba skrajna:

gdzie:

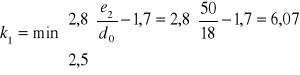
k₁= 2,5

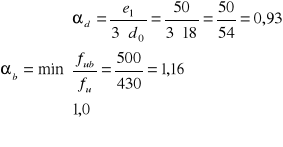
α_b= 0,93

-Śruby pośrednie:

gdzie:

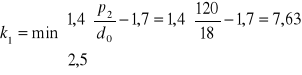
k₁= 2,5

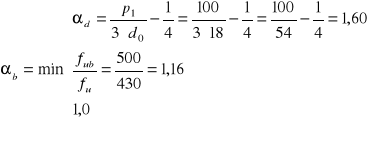
α_b= 1,0

Nośność grupy łączników

Nośność na rozerwanie blokowe panelu środnika belki:

gdzie:

Odp. Warunek spełniony

Przykładki

Nośność śruby na ścinanie wynosi:

Nośność śruby na docisk do środnika belki:

-Śruba skrajna:

gdzie:

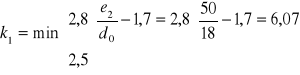
k₁= 2,5

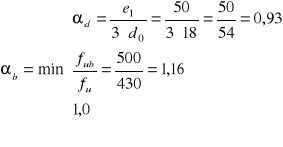
α_b= 0,93

-Śruby pośrednie:

gdzie:

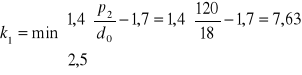
k₁= 2,5

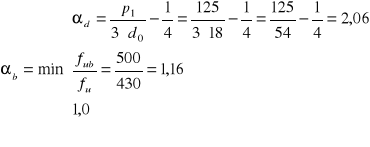
α_b= 1,0

Siła pochodząca od siły ścinającej

Siła pochodząca od momentu zginającego

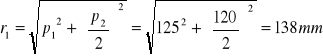
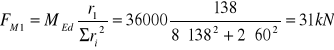
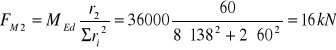
Siła w śrubach

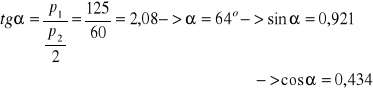
Odp. Warunek spełniony

Odp. Warunek spełniony

3.8 Sprawdzenie stanu granicznego użytkowalności.

3.8.1 Przęsło A-B

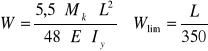
gdzie:

L= 10000 mm

I_y= 129431∙10⁴ mm⁴

E= 210000 N/mm²

M_k= α∙g∙L²+ß∙q∙L²= 0,0700∙21,655∙10²+0,09500∙38,5∙10²=517,335 kNm

Odp. Warunek jest spełniony.

---