Ewolucja stanu polaryzacji fotonu w materii

Ewolucja wektorów stanu polaryzacji fotonu w kalcycie

Rozpatrzymy ewolucję stanu polaryzacji fali świetlnej o częstości ω w ośrodku aktywnym optycznie, np. w kalcycie

Rys.10.1

Przyjmijmy, że oś optyczna
leży w płaszczyźnie podstawy prostopadłościennej próbki kalcytu. Niech spolaryzowana fala płaska pada prostopadle na boczną powierzchnię tej próbki. Dalej, przyjmijmy, że wektor
jest prostopadły także do osi optycznej kryształu. To oznacza, że podstawa leży w płaszczyźnie głównej kryształu (Rys. 3.2). Zgodnie z rozważaniami przedstawionym § 3.2 fala zwyczajna jest liniowo spolaryzowana w kierunku prostopadłym do płaszczyzny głównej i ma współczynnik załamania n_o, natomiast fala nadzwyczajna jest spolaryzowana liniowo w kierunku osi optycznej i ma współczynnik załamania n_e. Obydwie fale rozchodzą się w tym samym kierunku. Jak wiemy w przypadku kalcytu współczynniki załamania promienia spełniają nierówność
, a więc zgodnie ze wzorem (3.5) prędkości fazowe spełniają nierówność
. Zgodnie ze wzorem (3.15c) wyrazimy liczby falowe k_o, k_e przez częstość ω i współczynniki załamania
(i=e, o)

,
.

Ponieważ współczynniki załamania fali zwyczajnej i nadzwyczajnej różnią się w każdym punkcie z osi
wzdłuż której rozchodzą się te fale mają różne wyładniki czynników fazowych:
. Wektor stanu wiązki wchodzącej do bloku kalcytu (z=0) można przedstawić w postaci superpozycji

. (10.1)

W dowolnym punkcie
osi z składniki superpozycji (10.1) mają różne fazy

. (10.2a)

Wprowadzimy operator ewolucji stanu polaryzacji

. (10.3a)

Z jego pomocą możemy powiązać wektory stanu
i

. (10.2b)

Relacja (10.2b) jest spełniona dla wszystkich punktów osi z.

Wprowadzimy czas t potrzebny by światło rozchodzące się w próżni mogło przebyć drogę o długości z. Ponieważ
więc operator ewolucji (10.3a) można zapisać w postaci zależnej od czasu

.

Amplituda prawdopodobieństwa i prawdopodobieństwo zdarzenia polegającego na tym, że foton będący początkowo w stanie określonym przez wektor
poruszając się wzdłuż osi z po przebyciu drogi o długości l zachowa się jak gdyby był w stanie
równe są

,
.

Zbadajmy własności operatora
. Ponieważ operatory
,
są hermitow­skie i idempotentne (
) oraz spełnione są związki
, opera­tor
jest unitarny

. (10.4)

Rozpatrzymy iloczyn
. Wykorzystując te same, co w przypadku dowodu uni­tar­ności, własności operatorów rzutowania łatwo sprawdzić, że dla dowolnych z oraz a operatory
,
komutują i mają grupową własność

. (10.5a)

Z równania (10.5a) wynika, że

. (10.5b)

Jak widać dla każdego a spełniona jest relacja

. (10.5c)

Wektor stanu
można zapisać w postaci

. (10.5d)

10.2 Równanie ewolucji wektora stanu polaryzacji fotonu

Zbadajmy zmianę stanu polaryzacji na drodze
. Niech
, a zatem także
. Rozłożymy operator ewolucji
w szereg względem
(i=e,o) i pozostawimy dwa pierwsze wyrazy

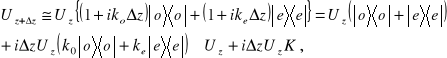
(10.6)

gdzie
jest hermitowskim operatorem wektora falowego

. (10.7)

Operatory
i
można przestawić

,

to znaczy, że ich komutator
znika

Nietrudno sprawdzić, że wektorami własnymi operatora wektora falowego są
i
, a od­powiadają im wartości własne

,
. (10.8)

Z tego powodu będziemy nazywać
operatorem wektora falowego. Jest to operator hermi­towski, zatem jego wartości własne są liczbami rzeczywistymi i można je zmierzyć w odpowiednim doświadczeniu. Wzór (10.7) określa rozkład spektralny operatora
.

Z równania (10.6) wynika, że operator ewolucji spełnia równanie różniczkowe zwy­czajne

, (10a)

z warunkiem początkowym

. (10.11a)

Po pomnożeniu obydwu stron tego równania z prawej strony przez wektor
otrzymamy

. (10.10b)

Równanie różniczkowe zwyczajne określa całą rodzinę rozwiązań. Aby wybrać któreś z nich należy zadać warunek początkowy. Niech początkowo układ znajduje się w stanie zadanym przez wektor stanu
. Wtedy warunek początkowy ma postać

. (10.11b)

Zapiszemy równanie (10.a,b) w jakiejś bazie, np.
. Otrzymamy parę równań różniczkowych

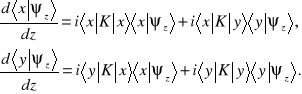
(10.10c),

Można ją zapisać w postaci zawierającej elementy macierzowe operatora wektora falowego

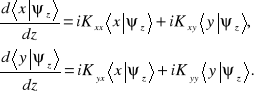
(10.10d)

W prowadzimy macierz
operatora
i składowe wektora stanu
w bazie kartezjańs­kiej x, y, wtedy wzór (10.10c) przyjmie postać

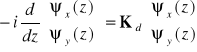
, (10.10e)

Dodajmy jeszcze warunki początkowe

. (10.11c)

Zbiór amplitud
jest dyskretnym odpowiednikiem funkcji falowej. Baza wektorów własnych może być parametryzowana przez parametr ciągły, tak jest np. w przypadku operatora położenia albo operatora pędu cząstki poruszającej się w przestrzeni. Wtedy, jak powiedzieliśmy, zbiór amplitud tworzy funkcję falową cząstki. Równania (10.10) są odpowiednikami równania Schrödingera, które spełniają wektory stanu zależne od czasu.

Ponieważ w czasie propagacji fali w krysztale fotony nie są pochłaniane amplituda fali, a więc i norma wektorów stanu polaryzacji nie powinny się zmieniać, tj. dla każdego
i z

.

Własność unitarności operatora ewolucji
zapewnia spełnienie tego warunku.

Rozwiązaniem równania (10.10a) z warunkiem początkowym
jest

. (10.12).

Z drugiej strony wektor
powinniśmy otrzymać mnożąc wektor wejściowy
przez operator ewolucji. To oznacza, że

. (10.3b)

O poprawności wzoru (10.3b) można się przekonać rozkładając operator wykładniczy w formalny szereg potęgowy i wykorzystując własności operatorów rzutowania
(j=e,o)

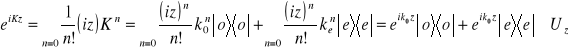
. (10.13)

Operator wektora falowego
, który przez związek (10.3b) jest związany z
- unitarnym operatorem ewolucji stanu polaryzacji, nazywać będziemy generatorem ewolucji wektora stanu polaryzacji. W przypadku przekształcenia infinitesimalnego (
) zmiana wektora stanu związana jest z generatorem ewolucji (wzór (10.9a)), natomiast zmiana składowych wektora stanu jest związana z macierzą reprezentującą generator ewolucji
w wybranej bazie (por. wzór (10.9b)).

10.3 Obraz Schrödingera ewolucji stanu polaryzacji fotonu

Rozpatrzymy propagację fali spolaryzowanej kołowo przez ciecz aktywną optycznie. Taką cieczą jest np. terpentyna i roztwór cukru. Jak poprzednio oś z kartezjańskiego układu współ­rzędnych jest równoległa do wektora
, natomiast osie x i y zorientowane są dowolnie. Niech fala rozchodzi się wzdłuż osi z i na drodze o długości d zmiana fazy wektora stanu
wynosi
, natomiast wektora stanu
wynosi (
). Zatem na drodze o długości
zmiana fazy
(
dla RCP,
dla LCP) stanów kołowo spolaryzowanych równa jest
. Jak widać na drodze dz fazy wektorów stanu kołowo spolaryzowanych zmieniają się proporcjonalnie do dz

.

Wektor stanu początkowego można przedstawić w postaci superpozycji

.

Podobnie możemy postąpić z wektorem stanu
. Ponieważ wiemy jak na drodze dz zmieniają się wektory
, możemy podać jawną postać wektora stanu
zależnego od długości drogi z przebytej przez foton w cieczy aktywnej optycznie

. (10.14)

Rozłożymy czynnik wykładniczy we wzorze (10.14) w szereg potęgowy i uwzględnimy to, że zgodnie z § 6.2
jest wektorem własnym operatora
odpowiadającego wartości własnej
.

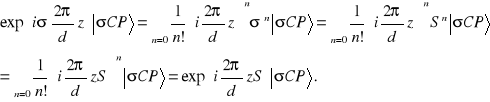
W odróżnieniu od zagadnienia propagacji fotonu przez kalcyt tym razem operator ewolucji
związany jest z operatorem momentu pędu fotonu

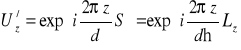
. (10.15)

Generator ewolucji ma postać

. (10.16)

Jak w poprzednim przypadku generator
jest hermitowski, bo operatory
i
są hermi­to­wskie

. (10.17)

Generatorem ewolucji w czasie jest operator Hamiltona
, który jest kwantowym odpowiednikiem klasycznej funkcji Hamiltona.

Operator ewolucji
spełnia równanie różniczkowe podobne do (10a)

, (10a)

z warunkiem początkowym

. (10.11a)

Jak w przypadku propagacji fali w kalcycie, wektor stanu
jest rozwiązaniem równania różniczkowego

. (10.18)

z warunkiem początkowym
.

Gdy wektory stanu fotonów zmieniają w wyniku ewolucji będziemy mówili o obrazie Schrödingera. W obrazie Schrödingera operatory charakteryzujące własności układu są stałe, natomiast ewoluują wektory stanu i ich iloczyny skalarne (czyli funkcje falowe). Zbadamy w obrazie Schrödingera ewolucję macierzy gęstości wywołaną rozcho­dze­niem się fali w cieczy aktywnej optycznie. Wykorzystamy spektralną postać macierzy gęstości (§ 9.4). Niech

będzie początkowym operatorem statystycznym. Wektory stanu ket i bra w punkcie z osi z mają postać (10.2b) z generatorem

,
.

Zatem w obrazie Schrödingera macierz gęstości się zmienia

. (10.22)

Po zróżniczkowaniu obydwu stron równania (10.22) otrzymamy

.

Jak widać w obrazie Schrödingera operator statystyczny spełnia równanie różniczkowe

, (10.23)

które odpowiada równaniu Liouville'a, określającego ewolucję zależnych od czasu operato­rów statystycznych. Można skonstruować opis układów kwantowych oparty na równaniu Liouville'a. Wymaga to podania warunku początkowego
, czyli zadania konkretnej postaci początkowej macierzy gęstości.

Po lewej stronie równania Liouville'a znajduje się komutator macierzy gęstości z generatorem ewolucji. Operator ewolucji jest funkcją wykładniczą generatora ewolucji, zatem komutator operatorów
i
znika

.

Sprawdzimy, że w reprezentacji polaryzacji liniowej operator ewolucji określa ma­cierz obrotu
. W tej bazie operator
reprezentowany jest przez macierz Pauliego
(8.7b). Jej parzysta potęga równa jest macierzy jednostkowej
, zaś nieparzysta jest równa

,
(k=0,1,2, ...)

By udowodnić sformułowaną tezę rozpatrzymy równanie, które spełnia operator ewolucji

.

Elementy macierzowe operatora ewolucji są rozwiązaniami układu równań różniczkowych

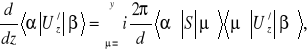
z warunkiem początkowym
. Znajdziemy równanie macierzowe odpowiadające w bazie x, y operatorowemu równaniu różniczkowemu. Po pomnożeniu przez
z lewej strony i
z prawej oraz wstawieniu pomiędzy operatory
i
jedynki operatorowej
otrzymamy równanie macierzowe

.

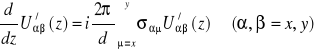
To macierzowe równanie ma następujące rozwiązanie

.

Zauważymy, że

.

Rozłożymy to rozwiązanie w formalny szereg potęgowy, który podzielimy na dwie części

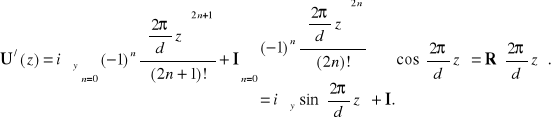
(10.24)

W ten sposób ustaliliśmy bardzo ważny fakt: generatorem obrotów dookoła osi z jest z-towa składowa operatora momentu pędu
. Przechodzenie światła przez ciecz aktywną optycznie powoduje skręcanie płaszczyzny polaryzacji.

10.3 Obraz Heisenberga ewolucji stanu polaryzacji

Ponieważ w tej części R. 10 będziemy rozpatrywać ewolucję wektorów stanu polaryzacji fotonów poruszających się w cieczy aktywnej optycznie opuścimy znak „prim” odróżniający operator ewolucji
(10.15) od
(10.3a). Zajmijmy się średnią wartością operatora
w stanie
i wyrazimy ją przez początkowe wektory stanu

.

Wprowadzimy oznaczenie

. (10.25)

Operator
zależy od drogi jaką przebył foton w ośrodku aktywnym optycznie. Mamy

. (10.26)

Lewą stronę równania (10.26) możemy uważać za zapisaną w obrazie Schrödingera, gdyż to wektory stanu zależą od z, natomiast operator nie zależy od tego parametru. Natomiast o prawej jego stronie mówimy, że jest zapisana w obrazie Heisenberga. W tym obrazie wektory stanu nie ewoluują, natomiast zmieniają się operatory zgodnie z regułą (10.25). Nietrudno sprawdzić, że pochodne po z obydwu stron równania (10.26) są równe.

Zróżniczkujemy obydwie strony równania (10.26) po z

.

Lecz

,
.

To oznacza, że operator
spełnia równanie różniczkowe

.

Ponieważ operatory
i
komutują możemy zapisać powyższe równanie w przypominającej równanie Heisenberga słuszne dla operatorów zmieniających się z upływem czasu

. (10.27)

Komutator
można także zapisać w postaci
.

Po prawej stronie równania Heisenberga, które spełniają operatory zmieniające się z upływem czasu znajduje się komutator z hamiltonianem
. W obrazie Heisenberga wektory stanu, funkcje falowe i operatory statystyczne nie zmieniają się. Zwrócimy uwagę na różnicę znaku komutatorów znajdujących się po prawej stronie równania Liouville'a (10.23) i równania Heisenberga (10.26).

10.4 Ewolucja układów kwantowych z upływem czasu

Można zadać pytanie czy wektory stanu w różnych chwilach czasu spełniają związki tego samego typu jak obowiązujące w przypadku ewolucji stanu polaryzacji fali rozchodzącej się w ośrodku aktywnym optycznie Odpowiedzi na to pytanie sformułujemy w postaci postulatów [2,3]. Postulaty te przypominają wyniki otrzymane dla wektorów stanu polaryzacji fotonów przechodzących przez ośrodki aktywne optycznie.

Postulat 1

Pierwszy postulat mówi o możliwości wprowadzenia obrazu Schrödingera także dla ewolucji związanej z upływem czasu. Niech
będzie wektorem stanu układu w chwili
. Istnieje jednoparametrowa rodzina unitarnych operatorów przekształcenia (ewolucji )

, (10.28)

określających zmianę
związaną z upływem czasu t

. (10.29)

Przekształcenia określane przez operator ewolucji zachowują normę

. (10.30)

Pokażemy, że unitarność operatora
wynika z grupowych własności ewolucji. Przyjmijmy, że interesujemy się ewolucją układu związaną z upływem czasu od dowolnej chwili t₁ do t. Lecz stan układu w chwili t₁ został osiągnięty w wyniku ewolucji od dowolnego wcześniejszego od t₁ momentu czasu t₀, zatem

. (10.31)

Jak widać

, (10.32a)

a to oznacza, że ewolucję w czasie możemy rozkładać na etapy. Kładąc
otrzymamy związek

,

Skąd wynika, że

. (10.32b)

Konsekwencją relacji (10.27b) jest unitarność operatora ewolucji
. Ponieważ

,

warunki (10.23) muszą być spełnione.

Postulat 2

Postulat drugi dotyczy istnienia generatora ewolucji w czasie. Generatorem
określającym ewolucję w czasie jest operator proporcjonalny do operatora Hamiltona układu

.

Tak jak znane nam generatory ewolucji
i
, Hamiltonian jest operatorem hermitowskim. Może on jawnie zależeć od czasu. Taka sytuacja ma miejsce gdy na układ działają zewnętrzne pola zależne od czasu. Większość współczesnych doświadczeń polega na badaniu odpowiedzi układów na różnego rodzaju pola zmieniające się z upływem czasu.

Zbadamy konsekwencje drugiego postulatu. Niech
będzie chwilą poprzedzającą moment czasu t. Na podstawie własności grupowych (10.32a) możemy napisać
. Lecz gdy
to
, i
. Przenosząc pierwszy wyraz ostatniego związku na lewą stronę, dzieląc obydwie strony tak przekształconego równania przez
i przechodząc do granicy
otrzymamy równanie różniczkowe, które spełnia operator ewolucji

. (10.33a)

Podobne równanie otrzymaliśmy dla ewolucji stanu polaryzacji fotonu. Warunek początkowy jaki spełnia operator ewolucji ma znaną postać

. (10.33b)

Nie trudno pokazać, ze równanie całkowe

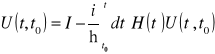
. (10.34)

jest równoważne równaniu różniczkowemu (10.28a). Spełnia ono warunek początkowy (10.28b). Równanie (10.29) stanowi podstawę wielu przybliżonych metod badania ewolucji układów kwantowych. By sprawdzić równoważność równań (10.28a) (10.29) trzeba zauważyć że pochodna funkcji
jest równa funkcji podcałkowej obliczonej dla argumentu x:
.

Zależne od czasu wektory stanu
spełniają równanie Schrödingera

. (10.35)

Nałożymy na wektor warunek początkowy
. Równanie Schrödingera równoważne jest równaniu całkowemu

.

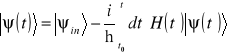
Gdy hamiltonian jawnie nie zależy od czasu to operator ewolucji przyjmuje prostą postać

. (10.36)

Zatem zależny od czasu wektor stanu jest proporcjonalny do czynnika wykładniczego

. (10.37)

Ograniczymy się do hamiltonianów niezależnych od czasu. Niech
,
będą wartościami własnymi i stanami własnymi hamiltonianu

. (10.38)

Ponieważ hamiltonian jest operatorem hermitowskim wartości własne
są liczbami rzeczywistymi. Zbiór wartości własnych
tworzy widmo energii. Widmo energii może być dyskretne, ciągłe albo mieć część dyskretną i ciągłą. Wektory własne hamiltonianu tworzą układ zupełny, a więc

. (10.39)

Gdy widmo energii jest ciągłe należy zamienić we wzorze (10.34) sumę na całkę.

Zajmijmy się amplitudą prawdopodobieństwa zdarzenia polegającego na tym, że układ w stanie
zachowuje się jak gdyby był w stanie

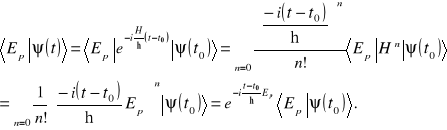
Wynika stąd wniosek, że układ znajdujący się w dowolnym stanie
na ogół nie ma określonej energii

.

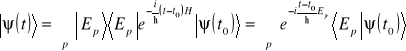
Jedynie gdy
to
, a stąd

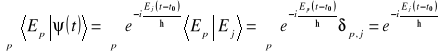
. (10.40)

To zaś oznacza, że układ będący w stanie o wektorze stanu
zawsze znajduje się w stanie
. O takim stanie mówimy, że jest stacjonarny.

Postulat 3

Jesteśmy już dobrze przygotowani do zrozumienia stwierdzeń następnego postulatu. Oto one: Wynikiem pomiaru energii układu jest jedna z wartości własnych hamiltonianu. Po wykonaniu pomiaru układ znajduje się w stanie własnym
odpowiadającym zmierzonej wartości własnej. Średnia wartość
otrzymana w wyniku wielokrotnych pomiarów na układami znajdującymi się w tym samym stanie
równa jest
.

Zbadajmy tę średnią wartość. Wykorzystamy związek (10.34)

.

Otrzymaliśmy wyrażenie podobne do (8.9). Jak założenia widać postulatu odpowiadają wynikom uzyskanym dla spolaryzowanych fotonów w § 8.1.

Literatura

[1] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974, R. 1.

[2] R.P. Feynman, R.B. Leighton, M. Sands, Feynmana wykłady z fizyki, Warszawa, PWN, 1972, R. 7, 8, 20.

[3] P. Roman, Quantum Mechanics, an Advanced Course, Addison-Wesley, Reading, Mass. 1965, § 1.5.

1

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---