2. POLE MAGNETYCZNE

2.1. Pole magnetyczne prądu elektrycznego

Doświadczalnie stwierdzono, że jeżeli w przewodzie, usytuowanym równolegle do ziemskiego południka magnetycznego, płynie prąd w kierunku jak na rys.2.1 i nad tym przewodem umieścić igłę magnetyczną, to biegun północny tej igły odchyli się w lewo.

Rys.2.1. Położenie igły magnetycznej umieszczonej nad przewodnikiem z prądem

Po zaniku prądu igła ustawi się w kierunku zgodnym z kierunkiem południka, a po zmianie kierunku prądu biegun północny igły odchyli się w prawo. Zależność kierunku wychylenia igły magnetycznej od kierunku prądu w przewodzie została sformułowana przez Ampère'a w postaci reguły, zwanej regułą Ampère'a lub regułą pływaka w postaci:

Biegun północny igły magnetycznej odchyla się ku lewej ręce człowieka płynącego w kierunku zgodnym z kierunkiem prądu elektrycznego i spoglądającego na igłę magnetyczną.

Z reguły tej wynika, że w przestrzeni otaczającej przewodnik z prądem, występują siły działające na igłę magnetyczną, która pod ich działaniem zajmuje ściśle określone położenia.

Stan przestrzeni, wewnątrz której na igłę magnetyczną oddziaływają siły, nazywa się polem magnetycznym.

Dalszym wnioskiem, wynikającym z opisanego wyżej doświadczenia, może być stwierdzenie, że wokół każdego przewodnika z prądem wytwarzane jest pole magnetyczne, i pole to jest ściśle związane z przepływem prądu elektrycznego. Kierunek ustawienia się igły magnetycznej w polu magnetycznym przyjęto nazywać kierunkiem pola magnetycznego. Umówiono się, że jako dodatni kierunek pola uważa się kierunek, w jakim zwrócony jest biegun północny igły magnetycznej.

Graficznie pole magnetyczne przedstawia się w postaci linii, stanowiących obwiednie położeń igły magnetycznej w polu magnetycznym (rys.2.2). Jak łatwo zauważyć, igła magnetyczna ustawia się w polu magnetycznym zgodnie z regułą Ampère'a, a obwiednie tych położeń tworzą współśrodkowe okręgi, których środek stanowi środek przewodnika z prądem. Obwiednie te nazywa się liniami sił pola magnetycznego lub liniami indukcji magnetycznej. Jako kierunek linii sił pola magnetycznego umówiono się przyjmować kierunek, wskazywany przez biegun północny igły magnetycznej. Kierunek ten zaznacza się za pomocą grotu strzałki. Pole magnetyczne otacza przewodnik na całej jego długości.

Rys.2.2. Pole magnetyczne wokół przewodnika z prądem elektrycznym: a) - dla kierunku prądu płynącego prostopadle do płaszczyzny kartki w głąb, b) - dla przeciwnego kierunku prądu prostopadłego do płaszczyzny kartki

Aby uniknąć konieczności stosowania igły magnetycznej do określania kierunku linii sił pola magnetycznego, sformułowano regułę, dotyczącą kierunku linii sił pola magnetycznego, płynącego w prostym przewodniku z prądem. Reguła ta nazywa się regułą korkociągu lub regułą śruby prawoskrętnej i brzmi następująco:

Jeżeli wkręcać korkociąg tak, aby jego ruch postępowy był zgodny z kierunkiem przepływu prądu w przewodniku, to wykonywany przy tym ruch obrotowy, wskazuje kierunek linii sił pola magnetycznego, wytworzonego wokół przewodnika.

Jeżeli przewodnik posiada kształt okrągłego zwoju, to kierunek linii sił pola magnetycznego jest taki, jak pokazano na przekroju takiego zwoju (rys.2.3). Łatwo zauważyć, że kierunki linii sił wewnątrz i na zewnątrz zwoju są jednakowe z tym, że ich zwroty wewnątrz i na zewnątrz zwoju są przeciwne. Ponadto można stwierdzić, że linie te są krzywymi zamkniętymi (bez początku i końca) i że z jednej strony wchodzą do zwoju, a z drugiej wychodzą.

Rys.2.3. Pole magnetyczne wokół przewodnika w kształcie okrągłego zwoju

W praktyce znalazły zastosowanie elementy złożone z wielu połączonych ze sobą szeregowo zwojów. Elementy takie nazywają się cewkami, solenoidami lub zwojnicami.

Rys.2.4. Pole magnetyczne wokół cewki

Jeżeli w cewce złożonej z pewnej liczby zwojów popłynie prąd elektryczny, to pola magnetyczne poszczególnych zwojów dodają się i wokół cewki zostanie wytworzone pole magnetyczne, którego linie sił przebiegają tak, jak to przedstawiono na rys.2.4. Z jednej strony linie sił wychodzą z wnętrza cewki, tworząc biegun magnetyczny, który umówiono się nazywać północnym N, a z drugiej wchodzą do wewnątrz cewki, tworząc biegun, który umówiono się nazywać południowym S. Podsumowując, można stwierdzić, że:

• cewka, przez którą przepływa stały prąd elektryczny, stanowi magnes trwały o dwóch biegunach,

• linie sił takiego magnesu są krzywymi zamkniętymi, wychodzącymi z bieguna północnego N, przebiegającymi na zewnątrz cewki i powracającymi do bieguna południowego S,

• wewnątrz cewki linie sił są równoległe do osi cewki.

1. Indukcja magnetyczna i strumień magnetyczny

Pole magnetyczne jest wielkością fizyczną, posiadającą w każdym punkcie określoną wartość i kierunek. Wielkości te można graficznie przedstawić za pomocą linii sił. W obszarze gdzie pole jest silniejsze, gęstość linii będzie większa i na odwrót. Kierunek pola oznacza się za pomocą naniesionych na linie strzałek o kierunku określonym według wcześniej omówionych zasad. Na razie jako silniejsze pole magnetyczne będzie przyjmowane takie pole, które z większą siłą oddziałuje na igłę magnetyczną.

Pole magnetyczne, które w każdym punkcie rozpatrywanego obszaru ma tę samą wartość i kierunek nazywa się polem jednorodnym.

Linie sił takiego pola rysuje się jako równo odległe od siebie proste równoległe. Doświadczalnie wykazano, że jeżeli w takim polu umieścić prostoliniowy przewodnik z prądem I, to na ten przewodnik będzie działała siła mechaniczna F, skierowana prostopadle do kierunku linii sił pola magnetycznego. Siła ta będzie również prostopadła do przewodnika (rys.2.5)




Rys.2.5. Oddziaływanie pola magnetycznego na przewodnik z prądem: a) - pole jednorodne i pole przewodnika z prądem, b) - pole wypadkowe i powstawanie siły mechanicznej

Jak widać na rys.2.5a, istnieją wtedy dwa pola: pole jednorodne (linie równoległe) i pole wytworzone przez przewodnik z prądem (współśrodkowe okręgi). Pola te nakładają się na siebie tworząc pole wypadkowe takie, jak przedstawione na rys.2.5b. Po prawej stronie przewodnika linie sił pola wytworzonego przez przewodnik są skierowane tak samo jak linie pola jednorodnego, a z lewej strony te same linie sił są skierowane przeciwnie do linii sił pola jednorodnego. Oznacza to, że pole magnetyczne po prawej stronie przewodnika jest wzmacniane, a po lewej osłabiane. W takim nierównomiernym polu na przewodnik z prądem działa siła mechaniczna, skierowana prostopadle do kierunki linii sił niezakłóconego pola.

Kierunek siły, działającej na przewodnik z prądem, umieszczony w jednorodnym polu magnetycznym, określa się na podstawie reguły prawej dłoni, która brzmi:

Jeżeli lewą dłoń ustawić tak, aby linie sił pola magnetycznego były prostopadłe do jej wewnętrznej powierzchni, a cztery palce będą wskazywały kierunek prądu w przewodniku, to odchylony kciuk wskaże kierunek siły, działającej na ten przewodnik.

Wartość siły F_p, działającej na przewodnik z prądem, jest proporcjonalna do długości l przewodnika i do natężenia płynącego w nim prądu I, tj.


(2.1)

przy czym B jest współczynnikiem proporcjonalności, charakteryzującym pole magnetyczne w danym punkcie. Wielkość ta nazywa się indukcją magnetyczną.

Indukcja magnetyczna jest wielkością wektorową, a zatem określa zarówno wartość, jak i kierunek pola magnetycznego w danym punkcie. Kierunek wektora indukcji jest zgodny z kierunkiem siły, działającym na biegun północny igły magnetycznej, a wartość indukcji jest jednostkowa, jeżeli na przewodnik o długości 1 metra (prostopadły do linii sił pola magnetycznego) z płynącym przez niego prądem o natężeniu 1 ampera, działa siła 1 niutona.




Rys.2.6. Graficzne przedstawienie jednorodnego pola magnetycznego

Graficznie wartość indukcji magnetycznej wyraża się przez gęstość linii sił, przypadającą na jednostkę powierzchni prostopadłej do tych linii. Tak więc, zgodnie z tą zasadą, jednorodne pole magnetyczne będzie przedstawione w postaci prostych równoległych o jednakowej gęstości we wszystkich punktach pola, tj.
(rys.2.5). Jeżeli na rys.2.5 przez S oznaczyć płaską powierzchnię, prostopadłą do linii sił pola magnetycznego (kierunek indukcji magnetycznej jest wtedy również prostopadły do tej powierzchni), to:

Iloczyn indukcji magnetycznej B przez powierzchnię S, prostopadłą do linii sił pola, nazywa się strumieniem magnetycznym Φ, przenikającym przez tę płaszczyznę.


(2.2)

Jeżeli pole magnetyczne jest niejednorodne, to należy rozpatrywać elementarny strumień magnetyczny
, przenikający przez elementarną powierzchnię
, prostopadła do kierunku indukcji magnetycznej B, tj.


(2.3)

Jednostkę indukcji magnetycznej B można określić z wzoru (2.1). Po przekształceniu tej zależności otrzymuje się, że


(2.4)

Z fizyki wiadomo, że związek między pracą i siłą jest zdefiniowany w ten sposób, że jeden dżul jest to praca, wykonana przez siłę jednego niutona na drodze 1 metra, co można zapisać matematycznie w postaci

. Ponieważ
, to jednostkę siły w wzorze (2.4) można wyrazić w następujący sposób:


(2.5)

Z równań (2.4) i (2.5) otrzymuje się ostatecznie


(2.6)

Woltosekunda Vs została nazwana weberem (symbol Wb), czyli 1 Vs = 1Wb. Zatem z (2.6) wynika, że jednostką indukcji magnetycznej jest jeden weber na metr kwadratowy


(2.7a)

lub, zgodnie z współczesnym nazewnictwem, jedna tesla (symbol T)


(2.7b)

Jednostką strumienia magnetycznego Φ, zgodnie z (2.2), jest jedna woltosekunda, czyli jeden weber


(2.8)

Przykład 2.1

W jednorodnym polu magnetycznym o indukcji magnetycznej
prostopadle do linii sił pola umieszczono przewodnik o długości
, w którym płynie prąd o natężeniu
. Obliczyć siłę mechaniczną F_p, działającą na ten przewodnik.

Rozwiązanie

Siłę mechaniczną, działającą na ten przewodnik, można obliczyć z zależności (2.1). Zgodnie z tą zależnością




Uwaga:

Zjawisko powstawania sił mechanicznych, działających na przewodnik, w którym płynie prąd elektryczny, jest wykorzystywane w silnikach elektrycznych.

2. Natężenie pola magnetycznego - przenikalność magnetyczna

Wewnątrz cewki, której długość jest znacznie większa od średnicy, podczas przepływu prądu elektrycznego pole magnetyczne jest praktycznie jednorodne, to znaczy, że linie sił pola są równoległe do osi cewki i indukcja magnetyczna jest we wszystkich punktach jednakowa
.

Związek indukcji magnetycznej wewnątrz cewki z jej długością i natężeniem płynącego w niej prądu ma postać


(2.9)

przy czym: μ - współczynnik proporcjonalności, zależny od ośrodka, w którym to pole występuje,

Iz = Θ - amperozwoje cewki, zwane również przepływem lub siłą magnetomotoryczną (symbol Θ),

I - natężenie prądu płynącego w cewce,

l - długość cewki.

Iloraz, występujący w wzorze (2.9), nazywa się natężeniem pola magnetycznego i jest najczęściej oznaczany symbolem H. Tak więc


(2.10)

Z zależności (2.10) wynika ważny wniosek, mianowicie że natężenie pola magnetycznego H wewnątrz cewki o długości l jest równe liczbie amperozwojów przypadających na jednostkę długości i nie zależy od właściwości ośrodka, w którym to pole występuje.

Z zależności tej można również określić jednostkę natężenia pola magnetycznego, a mianowicie


(2.11)

Równania (2.9) i (2.10) pozwalają ustalić związek między indukcją magnetyczną i natężeniem pola magnetycznego w postaci


(2.12)

Tak więc pole magnetyczne jest scharakteryzowane dwiema wielkościami B i H. Natężenie pola magnetycznego, podobnie jak indukcja magnetyczna, jest wielkością wektorową. Kierunek wektora natężenia pola jest zgodny z kierunkiem wektora indukcji magnetycznej. Doświadczalnie stwierdzono, że w próżni natężenie pola magnetycznego jest wprost proporcjonalne do indukcji n magnetycznej. Wynika to z faktu, że dla próżni wielkość
. We wszystkich innych ośrodkach wielkość ta nie jest stała, tj.
.

Występujący w wzorach (2.9) i (2.12) współczynnik proporcjonalności μ, nazywa się przenikalnością magnetyczną bezwzględną ośrodka, w którym występuje pole magnetyczne. Charakteryzuje ona własności magnetyczne materiałów, na które oddziałuje pole magnetyczne o natężeniu H.

Jednostkę przenikalności magnetycznej bezwzględnej można określić z równania (2.12), a mianowicie


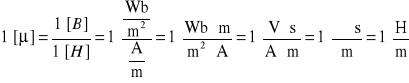
(2.13)

Uwaga:

Występujący w wzorze (2.13) symbol
jest jednostką indukcyjności (nie mylić z indukcją magnetyczną - są to zupełnie różne pojęcia), która zostanie zdefiniowana w dalszej części podręcznika.

W praktyce przenikalność magnetyczną przedstawia się w postaci iloczynu bezwzględnej przenikalności magnetycznej próżni
i względnej przenikalności magnetycznej ośrodka
, wskazującej ile razy przenikalność ośrodka jest większa od przenikalności próżni


(2.14)

przy czym

(2.15)

Dla próżni przenikalność magnetyczna
, czyli
. W praktyce przyjmuje się, że przenikalność próżni jest w przybliżeniu równa przenikalności magnetycznej powietrza.

Z przytoczonych rozważań wynika, że
charakteryzuje własności magnetyczne ciał, występujących w przyrodzie, w odniesieniu do przenikalności magnetycznej próżni.

W zależności od wartości
wszystkie ciała można podzielić na trzy grupy:

- diamagnetyki - ciała posiadające
< 1 (miedź, złoto, srebro, rtęć itp.),

- paramagnetyki - ciała posiadające
> 1 (aluminium, platyna, cyna i inne),

- ferromagnetyki - ciała posiadające
>> 1 (żelazo, nikiel, kobalt, stopy tych metali oraz niektóre stopy miedzi, manganu, metali z grupy ziem rzadkich).

O ile dla dwóch pierwszych grup względna przenikalność magnetyczna niewiele różni się od jedności, to w przypadku trzeciej grupy przenikalność ta osiąga wartości wielokrotnie większe. Ponadto względna przenikalność magnetyczna dla tej grupy ciał nie jest wielkością stała, lecz zależy od natężenia pola magnetycznego, tj.
.

Przykład 2.1

Dla cewki bez rdzenia jak na rys.2.7 obliczyć natężenie pola magnetycznego wewnątrz pierścienia cewki, indukcję magnetyczną oraz strumień magnetyczny przenikający przez pierścień. Dane cewki: średnica zewnętrzna
, średnica wewnętrzna
, liczba zwojów
, natężenie prądu w cewce
.




Rys.2.7. Cewka bez rdzenia magnetycznego

Rozwiązanie

Przy założeniu, że pole magnetyczne wewnątrz cewki jest jednorodne, jego natężenie można obliczyć z zależności (2.10)




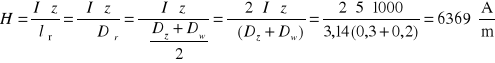
Indukcja magnetyczna w powietrzu, zgodnie z ogólną zależnością (2.12), jest równa
, a uwzględniając (2.14),
. Przyjmując, że bezwzględna przenikalność magnetyczna powietrza jest w przybliżeniu równa
, a względna
, otrzymuje się




Strumień magnetyczny oblicza się z zależności (2.2), tj.
, gdzie S jest przekrojem poprzecznym pierścienia cewki




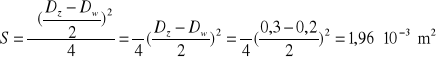
Ostatecznie strumień magnetyczny jest równy




2.4. Pole magnetyczne w żelazie

Jak już wcześniej wspomniano, przenikalność magnetyczna w ferromagnetykach, do których należy żelazo, jest zależna od natężenia pola magnetycznego. Przykładową zależność względnej przenikalności magnetycznej dla pewnego gatunku stali, przedstawiono na rys.2.8.




Rys.2.8. Przykładowa zależność względnej przenikalności magnetycznej żelaza od natężenia pola magnetycznego

Z wykresu
wynika, że dla natężenia pola około 150 A/m względna przenikalność magnetyczna
tego żelaza osiąga maksimum i wynosi około 3500 A/m, czyli jest tyle razy większa od przenikalności magnetycznej próżni. Oznacza to, że zastosowanie rdzenia ferromagnetycznego w cewce, zwiększa indukcję magnetyczną wewnątrz niej tyle razy, ile wynosi
zastosowanego materiału rdzenia, przy tym samym natężeniu pola magnetycznego. Widać to na przykładzie zależności na indukcję wewnątrz cewki przy braku rdzenia ferromagnetycznego
oraz z rdzeniem ferromagnetycznym
.

W praktyce korzysta się nie z zależności
lecz
. Wykresy tej ostatniej zależności nazywają się krzywymi magnesowania i są różne dla różnych gatunków ferromagnetyków. Krzywe magnesowania określa producent materiału ferromagnetycznego. Przykładowe przebiegi takich krzywych przedstawiono na rys.2.9.




Rys.2.9. Krzywe magnesowania dla blachy twornikowej, staliwa i żeliwa

Z przebiegu krzywych magnesowania wynika, że dla małych wartości natężenia pola magnetycznego indukcja magnetyczna rośnie prawie proporcjonalnie do natężenia pola magnetycznego. Przy dalszym wzroście natężenia pola magnetycznego następuje zagięcie (tzw. „kolano”) krzywej magnesowania, co oznacza, że indukcja magnetyczna w otoczeniu zagięcia przestaje zmieniać się proporcjonalnie do natężenia pola magnetycznego. Dalsze zwiększanie natężenia pola magnetycznego powoduje już tylko nieznaczne przyrosty indukcji magnetycznej, przy czym przyrosty te są znowu prawie proporcjonalne do przyrostów natężenia pola. Mówi się wtedy, że ferromagnetyk znajduje się w stanie nasycenia.

Jeżeli ferromagnetyk jest magnesowany po raz pierwszy, to proces magnesowania przebiega według krzywej 0-1 (rys.2.10), która nazywa się krzywą magnesowania pierwotnego. Jeżeli po osiągnięciu punktu 1, zmniejszać natężenie pola magnetycznego (zmniejszając prąd płynący w cewce), to zmiany indukcji magnetycznej będą zachodzić według krzywej 1-2, leżącej powyżej krzywej magnesowania pierwotnego. Mimo że w punkcie 2 natężenie pola magnetycznego jest równe zeru, indukcja magnetyczna ma pewną wartość B_sz, odpowiadającą rzędnej 0-2. Indukcję tę nazywa się indukcją szczątkową lub indukcją remanentu.




Rys.2.10. Pętla histerezy ferromagnetyka

Aby zmniejszyć indukcję magnetyczną do zera, należy odwrócić kierunek prądu magnesującego w cewce. Powoduje to zmianę kierunku natężenia pola magnetycznego na przeciwny. Przy natężeniu pola, odpowiadającym odciętej 0-3, indukcja magnetyczna jest ponownie równa zeru. Mówi się wtedy, że ferromagnetyk został rozmagnesowany. Natężenie pola likwidujące magnetyzm szczątkowy nazywa się natężeniem powściągającym lub koercją.

Zwiększając dalej ujemne natężenie pola do wartości -H_max, zwiększa się indukcję magnetyczną do wartości -B_max, przy czym zmiany indukcji zachodzą według krzywej 3-4. Przy zmniejszaniu ujemnego natężenia pola magnetycznego do zera, przemagnesowanie odbywa się według krzywej 4-5 i kończy uzyskaniem ujemnej wartości indukcji szczątkowej -B_sz .

Jeżeli teraz ponownie zmienić kierunek prądu i zwiększać natężenie pola magnetycznego do wartości H_max, to proces magnesowania będzie przebiegał według krzywej 5-6-1, a indukcja ponownie osiągnie wartość B_max.

Z przytoczonych rozważań wynika, że przemagnesowywanie ferromagnetyków, przy zmianie natężenia pola magnetycznego od H_max do -H_max i z powrotem do H_max odbywa się według zamkniętej krzywej 1-2-3-4-5-6-1, zwanej pętlą histerezy magnetycznej. Pętla ta odpowiada jednemu cyklowi przemagnesowania ferromagnetyka.

Aby wyjaśnić taki przebieg przemagnesowania, należy zauważyć, że podczas każdego cyklu przemagnesowania wykonywana jest pewna praca. Ponieważ ferromagnetyki są ciałami zbudowanymi z cząsteczek, będących elementarnych magnesami zwanymi dipolami, to podczas cyklu przemagnesowania dipola nieustannie zmieniają swoje położenie, Występujące przy tym tarcie międzycząsteczkowe, powoduje wydzielanie się ciepła w ferromagnetyku, odpowiadające pracy zużytej na przemagnesowanie. Można wykazać, że praca zużyta na przemagnesowanie zależy od powściągającego natężenia pola magnetycznego, czyli od szerokości pętli histerezy, a pole ograniczone tą pętlą jest wprost proporcjonalne do pracy zużytej na przemagnesowanie.

Ze względu na szerokość pętli histerezy materiały magnetyczne dzieli się na dwie grupy:

- materiały magnetycznie twarde, np. stale z dodatkiem niklu, chromu lub wolframu, stopy z metalami z grupy metali ziem rzadkich (neodym, samar) i szereg innych, które odznaczają się szerokimi pętlami histerezy, tj. dużymi wartościami powściągającego natężenia pola H_k i dużymi wartościami indukcji szczątkowej B_sz (rys.2.11a),

- materiały magnetycznie miękkie, np. stal z dodatkiem krzemu, o wąskich pętlach histerezy, tj. o małych wartościach powściągającego natężenia pola H_k i małych wartościach indukcji szczątkowej B_sz (rys.2.11b).




Rys.2.11. Pętle histerezy materiałów magnetycznych: a) - magnetycznie twardych, b) - magnetycznie miękkich

Materiały magnetycznie twarde są używane do produkcji magnesów trwałych, a materiały magnetycznie miękkie do produkcji rdzeni, które podlegają cyklicznemu przemagnesowywaniu, np. rdzeni transformatorów, dławików, maszyn prądu przemiennego itp.).

1. . Obwody magnetyczne

Obwodem magnetycznym nazywa się drogę, po której zamyka się strumień magnetyczny. Przykładem może być rdzeń elektromagnesu, przedstawionego na rys.2.12.




Rys.2.12. Elektromagnes

Na rdzeniu żelaznym w kształcie podkowy nawinięta jest cewka, przez którą przepływa prąd magnesujący. Przy kierunku prądu jak na rysunku 2.12, zgodnie z regułą korkociągu, powstają bieguny N i S. Dla przypomnienia, biegunem północnym N umówiono się nazywać biegun, z którego wychodzą linie sił pola magnetycznego, a biegunem południowym S - biegun, do którego linie sił wchodzą. Bieguny magnetyczne są połączone zworą, zwaną również kotwicą. Otrzymuje się w ten sposób obwód magnetyczny, w którym strumień magnetyczny na całej jego drodze przebiega żelazie. Przekroje rdzenia o kształcie podkowy i zwory są na ogół takie same.

Strumień magnetyczny
(wzór 2.2), a ponieważ indukcja magnetyczna w żelazie, zgodnie z (2.10) i (2.12), wynosi
, to podstawiając ostatnie wyrażenie do pierwszego wzoru, otrzymuje się


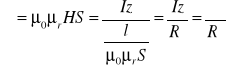
(2.16)

Zależność


(2.17)

jest nazywana prawem Ohma dla obwodów magnetycznych. Dla przypomnienia, prawo Ohma dla obwodów elektrycznych ma postać
, przy czym napięcie U jest wymuszeniem, powodującym przepływ prądu elektrycznego, a R wielkością charakteryzująca własności drogi (rezystancję), po której płynie prąd elektryczny. W zależności (2.17) wymuszeniem, powodującym przepływ strumienia magnetycznego, jest przepływ
, zwany również amperozwojami lub siłą magnetomotoryczną (jednostką jest 1A), a strumień Φ jest analogiem prądu elektrycznego I w prawie Ohma dla obwodów elektrycznych.

Wielkością charakteryzującą własności drogi strumienia, jest oporność magnetyczna R_μ, zwana również reluktancją


(2.18)

Jednostką reluktancji
jest


= 1 [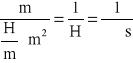
]

W użyciu jest również wielkość, będąca odwrotnością reluktancji, nazywana przewodnością magnetyczną lub permeancją


(2.19)

Jednostką permeancji jest

1 [
] = 1


Jeżeli obwód magnetyczny składa się z kilku odcinków o różnych długościach
,
,
i różnych przekrojach S₁, S₂, S₃ , to całkowita reluktancja obwodu magnetycznego jest równa sumie reluktancji poszczególnych odcinków


(2.20)

a strumień magnetyczny


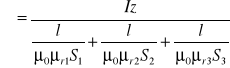
(2.21)

stąd


(2.22)

Ponieważ
, to, równanie (2.22) można przepisać w postaci


(2.23)

Zależność (2.23) można uogólnić na dowolną liczbę cewek i odcinków i zapisać w postaci



(2.24)

przy czym: H_i - natężenie pola magnetycznego w i-tym odcinku obwodu magnetycznego,

l_i - długość i-tego odcinka obwodu magnetycznego,

n - liczba odcinków obwodu magnetycznego,

i - numer odcinka obwodu magnetycznego

I_k - natężenie prądu w k-tej cewce,

z_k - liczba zwojów k-tej cewki

m - liczba cewek

k - numer cewki.

Równanie (2.23) można uważać za odpowiednik II prawa Kirchhoffa dla obwodów elektrycznych. Przepływ
jest odpowiednikiem napięcia U lub SEM, a iloczyny
- odpowiednikami spadków napięć
. W wielu podręcznikach iloczyny
są wręcz nazywane spadkami napięcia magnetycznego.

W stosowanych w praktyce obwodach magnetycznych, część strumienia zamyka się zazwyczaj przez powietrze. Przykładem może być elektromagnes ze zworą, nie przylegającą do biegunów rdzenia (rys.2.13).




Rys.2.13. Elektromagnes z rdzeniem zawierającym szczelinę powietrzną

Wytworzony przez przepływ strumień magnetyczny Φ, przebiega w podkowie rdzenia prawie nie zmieniając swojej wartości, natomiast do zwory przenika strumień Φ_zw, mniejszy od strumienia Φ. Strumień Φ_zw przepływający przez zworę, nazywa się strumieniem użytkowym, natomiast pozostała część strumienia, zamykająca się między biegunami przez powietrze, nazywa się strumieniem rozproszenia Φ_r. Strumień całkowity jest więc równy sumie strumienia użytkowego i strumienia rozproszenia


(2.25)

Przykład 2.2

Cewka o wymiarach i liczbie zwojów jak w przykładzie 2.1 (
) jest nawinięta na rdzeniu wykonanym: a) - z żeliwa, b) - ze staliwa. Obliczyć strumień magnetyczny i indukcję magnetyczną w rdzeniu.

Rozwiązanie

Ad.a).

Jak wiadomo, natężenie pola magnetycznego nie zależy od ośrodka, w którym to pole występuje, więc w cewce z rdzeniem będzie ono takie samo jak w cewce bez rdzenia




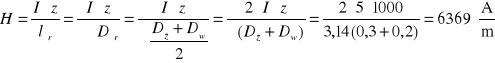
Dla tej wartości natężenia pola, z krzywej magnesowania żeliwa
odczytano odpowiadającą temu natężeniu wartość indukcji magnetycznej
.

Strumień magnetyczny, przenikający przez powierzchnię S pierścienia cewki dla pola jednorodnego wynosi




Przenikalność magnetyczna bezwzględna żeliwa dla indukcji 0,84 T wynosi





a przenikalność magnetyczna względna żeliwa


[-]

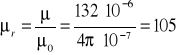
Porównując wyniki obliczeń dla cewki bez rdzenia i cewki z rdzeniem żeliwnym, widać, że w przypadku cewki z rdzeniem żeliwnym indukcja magnetyczna i strumień magnetyczny są 105 raz razy większe niż w przypadku cewki bez rdzenia.

Ad.b).

Dla wartości natężenia pola jak w punkcie a), tj.

z krzywej magnesowania dla staliwa odczytuje się wartość indukcji magnetycznej
.

Strumień magnetyczny, przenikający przez powierzchnię S pierścienia cewki z rdzeniem ze staliwa dla pola jednorodnego wynosi




Przenikalność magnetyczna bezwzględna żeliwa dla indukcji 1,67 T wynosi




a przenikalność magnetyczna względna staliwa




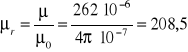
Porównując wyniki obliczeń dla cewki bez rdzenia i cewki z rdzeniem ze staliwa widać, że w przypadku cewki z rdzeniem ze staliwa indukcja magnetyczna i strumień magnetyczny są 208,5 razy większe niż w przypadku cewki beż rdzenia.

Z przytoczonego przykładu wynikają następujące wnioski:

- stosowanie rdzeni ferromagnetycznych w cewkach elektromagnesów pozwala wielokrotnie zmniejszyć amperozwoje niezbędne do wytworzenia określonego strumienia magnetycznego wewnątrz cewki i zaoszczędzić materiały, z których wykonane są cewki (mniej zwojów lub mniejsze przekroje drutów nawojowych).

- w przypadku projektowania cewek z rdzeniami ferromagnetycznymi, korzystniej jest stosować rdzenie wykonane z ferromagnetyków o większej względnej przenikalności magnetycznej (w rozpatrywanym przypadku zastosowanie staliwa zamiast żeliwa zwiększa strumień magnetyczny i indukcję magnetyczną prawie dwukrotnie)

Przykład 2.3

Cewka o wymiarach i liczbie zwojów jak w przykładzie 2.1 (
) jest nawinięta na rdzeniu wykonanym ze staliwa z tym, że w rdzeniu wykonana jest szczelina o długości
tak, jak to przedstawiono na rys.2.14. Obliczyć przepływ (amperozwoje) niezbędny do wytworzenia w obwodzie magnetycznym strumienia magnetycznego o wartości jak w przykładzie 2.2b, tj.
.

?

Rys.2.14. Cewka na rdzeniu ferromagnetycznym ze szczeliną powietrzną

Rozwiązanie

W tym przypadku obwód magnetyczny składa się z dwóch odcinków: odcinka o długości l_{s t}= l_śr - l_δ, w którym strumień magnetyczny przebiega w ferromagnetyku (staliwo) i odcinka o długości l_δ, w którym strumień przebiega w powietrzu.

Długość drogi w powietrzu wynosi
, a długość drogi w stali




Przekrój rdzenia wynosi




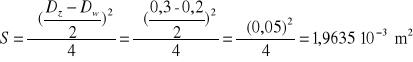
Zakłada się, że zarówno w stali jak i w powietrzu pole magnetyczne jest jednorodne (
). Wartość indukcji w stali można wtedy obliczyć z wzoru




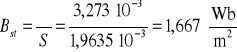
a wartość indukcji magnetycznej odczytać z krzywej magnesowania dla staliwa. W danym przypadku indukcji magnetycznej o wartości
odpowiada natężenie pola magnetycznego
.

Natężenie pola magnetycznego w szczelinie oblicza się z wzoru




Na podstawie wzoru (2.24) dla
i
otrzymuje się zależność, z której można obliczyć amperozwoje, niezbędne do wytworzenia wymaganej wartości strumienia w rdzeniu




Z powyższych obliczeń wynika bardzo istotna dla obwodów magnetycznych właściwość, a mianowicie, że na przeprowadzenie strumienia magnetycznego przez szczelinę powietrzną, potrzeba znacznie więcej amperozwojów niż na przeprowadzenie tego samego strumienia przez rdzeń ferromagnetyczny. W rozpatrywanym przypadku, liczba amperozwojów przypadających na jednostkę długości drogi w powietrzu, jest około 240 razy większa od liczby amperozwojów, przypadających na jednostkę długości drogi w stali.

2. . Oddziaływanie elektrodynamiczne przewodników z prądem

Jeżeli dwa przewodniki z prądem są usytuowane względem siebie równolegle i w przewodnikach tych płyną prądy, to na takie przewodniki oddziałują siły mechaniczne. Niżej zostaną rozpatrzone dwa przypadki, różniące się kierunkami przepływu prądu w przewodnikach (rys.2.15).

Na rys.2.15a kierunek prądu I₁ w pierwszym przewodniku jest taki sam jak kierunek prądu I₂ w drugim przewodniku. Przewodniki mają długość l i znajdują się w odległości a od siebie. Wokół tak usytuowanych przewodników z prądem wytwarzane są pola magnetyczne. Kierunki linii sił tych pól można określić stosując regułę korkociągu. Oczywiście pola te nakładają się na siebie, odejmując się w przestrzeni między przewodnikami, i dodając na zewnątrz przewodników. W wyniku tego między przewodnikami pole zostanie osłabione (linie sił rozrzedzone), a na zewnątrz wzmocnione (linie sił zagęszczone). Skutkiem tego jest powstanie sił mechanicznych, powodujących przyciąganie się przewodników.




Rys.2.15. Oddziaływanie elektrodynamiczne przewodników z prądem: a) - przy jednakowych kierunkach prądów, b) - przy różnych kierunkach prądów

Na rys.2.15b kierunki prądów w przewodnikach są przeciwne. W tym przypadku wzmocnienie pola (zagęszczenie linii sił) wystąpi między przewodnikami, a osłabienie (rozrzedzenie linii sił) na zewnątrz przewodników. Skutkiem tego jest powstanie sił mechanicznych, powodujących wzajemne odpychanie się przewodników.

Wzajemne przyciąganie się lub odpychanie przewodników z prądem nazywa się oddziaływaniem elektrodynamicznym.

Siła F, z którą przyciągają się lub odpychają dwa równoległe przewodniki z prądami I₁ i I₂ jest wprost proporcjonalna do natężenia prądów i długości tych przewodników oraz odwrotnie proporcjonalna do odległości między nimi. Siłę tę można obliczyć z zależności


(2.26)

przy czym: μ₀ - bezwzględna przenikalność magnetyczna powietrza (w przybliżeniu równa przenikalności bezwzględnej próżni) w henrach na metr,


- natężenia prądów w przewodach w amperach,

l - długość przewodów w metrach,

a - odległość między przewodami w metrach,

F - siła działająca na każdy z przewodów w niutonach.

Zależność (2.26) została wykorzystana do zdefiniowania jednostki natężenia prądu w międzynarodowym układzie jednostek MKSA. Definicja ta ma następujące brzmienie:

Amper jest natężeniem takiego prądu elektrycznego, który płynąc w umieszczonych w próżni dwóch równoległych prostoliniowych przewodach odległych od siebie o 1 metr, o okrągłych znikomo małych przekrojach i nieskończonej długości, wytwarza między tymi przewodami siłę niutonów, działającą na każdy metr długości przewodów.

Oddziaływanie elektrodynamiczne przewodów z prądem może być niekiedy niebezpieczne. Dotyczy to przypadków, kiedy prądy w przewodach osiągają duże wartości, a odległość między przewodami nie jest zbyt duża. Duże wartości prądów występują zazwyczaj w stanach awaryjnych, np. podczas zwarć w sieciach. W rozdzielniach elektroenergetycznych, powstające podczas zwarć siły, mogą uszkodzić prowadzone równolegle do siebie i zamocowane na izolatorach wsporczych szyny zbiorcze. Wytwarzane podczas zwarć naprężenia mechaniczne mogą spowodować odkształcenia szyn, a także powyginanie lub połamanie izolatorów wsporczych. Siły elektrodynamiczne powstające podczas zwarć są również niebezpieczne dla cewek o kształcie prostokątnym. W cewkach takich prądy w przeciwległych bokach płyną w przeciwnych kierunkach i siły działające na przewody wytwarzają naprężenia rozrywające te cewki.

Przykład 2.4

Obliczyć siły mechaniczne F działające na 1 metr bieżący szyn zbiorczych, biegnących równolegle w odległości a=10 cm od siebie, jeżeli prąd zwarciowy I_zw=50kA.

Rozwiązanie

Podczas zwarcia w każdej szynie płynie taki sam prąd zwarciowy, więc zależność na siłę oddziaływania elektrodynamicznego przewodów ma postać




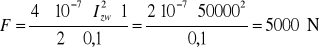
Ponieważ 9,81 N=1 kG, to na 1 metr bieżący szyn działa siła około 510 kG.

3. . Indukcja elektromagnetyczna

Jeżeli w jednorodnym polu magnetycznym umieścić prosty przewodnik o długości l i przemieszczać go w kierunku prostopadłym do linii sił pola z prędkością v, to dołączony do końców przewodnika galwanometr wykaże, że w takim przewodniku jest wytwarzana pewna siła elektromotoryczna (SEM). Jeżeli ten sam przewodnik przemieszczać z tą samą prędkością zgodnie z liniami sił pola, to galwanometr nie wykaże żadnej SEM. Znaczy to, że warunkiem wytwarzania w ruchomym przewodniku SEM, jest przecinanie przez ten przewodnik linii sił pola magnetycznego.

Zjawisko wzbudzania siły elektromotorycznej w przewodniku przecinającym linie pola magnetycznego nazywa się indukcją elektromagnetyczną, a siłę elektromotoryczną powstającą w przewodniku siłą elektromotoryczną indukowaną lub SEM indukcji.

Kierunek indukowanej w przewodniku SEM indukcji zależy od kierunku ruchu przewodnika i od kierunku linii sił pola magnetycznego. Określa się go za pomocą reguły prawej dłoni, która brzmi:

Jeżeli prawą dłoń ustawić w ten sposób, że linie sił pola padają na wewnętrzną powierzchnię dłoni, a odchylony kciuk pokazuje kierunek ruchu przewodu, to pozostałe wyprostowane palce wskażą kierunek indukowanej w przewodzie siły elektromotorycznej.

Wykazano, że wartość SEM E indukowanej w przewodniku, poruszającym się w jednorodnym polu magnetycznym (
), jest wprost proporcjonalna do indukcji magnetycznej pola B, długości przewodnika l i prędkości v z jaką ten przewodnik porusza się w kierunku prostopadłym do kierunku linii sił pola,tj.


(2.27)

Jeżeli w wzorze (2.27) indukcję magnetyczną wyrazić w teslach, długość przewodnika w metrach, a prędkość w metrach na sekundę, to SEM indukcji będzie wyrażona w voltach, ponieważ




Zjawisko indukcji elektromagnetycznej jest wykorzystywane praktycznie w prądnicach (generatorach), tj. elektromaszynowych przetwornikach energii mechanicznej na energię elektryczną.

Przykład 2.5

Obliczyć siłę elektromotoryczną indukowaną w przewodniku o długości
, poruszającego się w jednorodnym polu magnetycznym o indukcji
prostopadle do linii sił z prędkością liniową
.

Rozwiązanie

Zgodnie z zależnością (2.27), SEM indukowana w przewodniku wynosi




Badania wykazały, że SEM indukcji występuje nie tylko w przewodniku, poruszającym się w polu magnetycznym prostopadle do linii sił, ale również w każdym zamkniętym obwodzie, np. zwoju, przez który przenika strumień magnetyczny Φ, jeżeli w elementarnym czasie
następuje zmiana strumienia o elementarną wartość
, tj.


(2.28)

Uwaga:

SEM indukowaną w wyniku zmiany strumienia magnetycznego w czasie, oznacza się małą literą e, ponieważ wielkość ta nie jest stała w czasie. Analogicznie, prąd płynący pod wpływem tej SEM, oznacza się małą literą i. Prąd ten nazywa się też prądem indukowanym.

W zamkniętym obwodzie elektrycznym, w którym indukuje się SEM indukcji e, popłynie prąd indukowany i o kierunku zgodnym z kierunkiem SEM (rys.2.16). Prąd ten wytwarza własny strumień magnetyczny
, o kierunku zgodnym z regułą korkociągu. Okazało się, że strumień ten jest równy co do wartości strumieniowi
, który wyidukował SEM, lecz jest przeciwnie skierowany. Ponieważ jako dodatni kierunek strumienia umówiono się przyjmować ten, który odpowiada kierunkowi wyznaczonemu za pomocą reguły korkociągu, to strumień
będzie strumieniem dodatnim, a strumień
, który jest skierowany przeciwnie - strumieniem ujemnym.




Rys.2.16. Rysunek wyjaśniający zjawisko indukcji elektromagnetycznej

Ponieważ SEM e oraz prąd i mają kierunki zgodne, to dla otrzymania z zależności (2.28) dodatniej wartości e, przyrostowi strumienia
należy przypisać znak ujemny. Zależność (2.28) przyjmuje wtedy postać


(2.29)

Z analizy równania (2.29) wynika, że dodatnim przyrostom strumienia w czasie odpowiada ujemny kierunek indukowanej SEM i odwrotnie. Zostało to uogólnione w postaci reguły Lenza, zwanej niekiedy regułą przekory, która brzmi:

Kierunek prądu indukowanego w obwodzie zamkniętym jest zawsze taki, że strumień wytworzony przez ten prąd, przeciwdziała zmianie strumienia magnetycznego, przenikającego przez ten obwód.

Jeżeli obwód zamknięty składa się nie z jednego zwoju lecz z z połączonych szeregowo zwojów, to zależność (2.29) przybiera wtedy postać


(2.30)

Zależność ta dotyczy tylko tych przypadków, kiedy wszystkie zwoje są w każdej chwili skojarzone z tym samym strumieniem magnetycznym (strumień przenika jednocześnie przez wszystkie zwoje). Ma to miejsce wtedy, gdy zwoje są nawinięte na rdzeniu ferromagnetycznym blisko siebie.

Wzór (2.30) jest ogólnym zapisem matematycznym prawa indukcji elektromagnetycznej, określającym związek między wielkościami elektrycznymi i magnetycznymi. Rozpatrywane wcześniej zjawisko indukowania się SEM w prostym przewodniku, przemieszczającym się w jednorodnym polu magnetycznym prostopadle do linii sił pola, jest przypadkiem szczególnym ogólnego prawa indukcji elektromagnetycznej.

Wszystkie zjawiska zachodzące w maszynach elektrycznych wirujących (silniki, prądnice) oraz transformatorach, można rozpatrywać jako oparte na indukowaniu się SEM w przewodnikach, znajdujących się w zmiennym polu magnetycznym.

4. . Samoindukcja

W przypadkach rozpatrzonych w poprzednim rozdziale, indukowanie się siły elektromotorycznej E w przewodniku lub e w zamkniętym obwodzie elektrycznym, było spowodowane przyczynami, występującymi poza rozpatrywanym obwodem (ruch przewodnika w polu magnetycznym, zmiana zewnętrznego strumienia magnetycznego w czasie). Okazuje się jednak, że indukowanie SEM e w obwodzie elektrycznym może spowodować również zmiana strumienia w czasie, wywołana zmianą prądu
, płynącego w tym samym obwodzie. Dodatni elementarny przyrost prądu
odbywający się w elementarnym czasie
, spowoduje elementarny przyrost strumienia magnetycznego
, skierowany zgodnie z regułą korkociągu tak, jak na rys.2.17.




Rys.2.17. Rysunek wyjaśniający zjawisko samoindukcji

Strumień ten jest sprzężony z rozpatrywanym obwodem, więc jego przyrost w czasie spowoduje wyidukowanie się siły elektromotorycznej e we własnym obwodzie. Wyidukowaną w ten sposób SEM nazywa się siłą elektromotoryczną samoindukcji i oznacza symbolem
. SEM samoindukcji jest opisana zależnością analogiczną (2.29), opisującą SEM indukcji elektromagnetycznej, tj.


(2.31)

Zjawisko wytwarzania w obwodzie SEM, indukowanej w wyniku zmian czasowych prądu w tym samym obwodzie, nazywa się samoindukcją lub indukcją własną.

Zgodnie z prawem Lenza, można również powiedzieć, że SEM samoindukcji przeciwdziała przyczynie, która ją wywołała. Przy narastaniu prądu w obwodzie (+di) SEM samoindukcji
ma kierunek przeciwny do kierunku prądu i przeciwdziała wzrostowi tego prądu. Przy zanikaniu prądu w obwodzie SEM samoindukcji
ma kierunek zgodny z kierunkiem prądu i przeciwdziała jego zanikaniu.

Zjawisko samoindukcji można porównać z zjawiskiem bezwładności w mechanice.

Jeżeli cewka składa się z z szeregowo połączonych zwojów, to podczas elementarnej zmiany strumienia
w elementarnym czasie
, spowodowanej zmianą natężenia prądu w cewce
, to wyidukowana w cewce SEM
jest z razy większa i wynosi


(2.32)

Strumień magnetyczny wytworzony przez cewkę, zgodnie z (2.17), jest równy




przy czym
jest opornością magnetyczną (reluktancją) obwodu. Przyjmując
, z równań (2.17) i (2.32) otrzymuje się


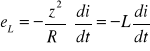
[V] (2.33

Występujący w równaniu (2.33) symbol L jest współczynnikiem proporcjonalności i nazywa się indukcyjnością lub współczynnikiem samoindukcji obwodu prądowego


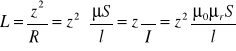
(2.34)


(2.35)

Z powyższego równania wynika, że indukcyjność L obwodu zależy od jego wymiarów geometrycznych oraz od przenikalności magnetycznej
ośrodka, w którym występuje strumień magnetyczny Φ, wytworzony przez prąd płynący w tym obwodzie. Jeżeli strumień magnetyczny występuje w powietrzu, to indukcyjność L jest wielkością stałą, jeżeli zaś strumień zmyka się przez żelazo, to indukcyjność L nie jest wielkością stałą, bowiem względna przenikalność magnetyczna żelaza zależy od natężenia pola magnetycznego.

Z powyższych rozważań wynika również, że indukcyjność cewki z rdzeniem żelaznym będzie zawsze znacznie większa od indukcyjności cewki bez rdzenia, gdyż przenikalność magnetyczna żelaza jest znacznie większa od przenikalności magnetycznej powietrza (do kilku tysięcy razy).

Jednostkę indukcyjności można określić z zależności (2.33) lub (2.34). Wykorzystując tę ostatnią otrzymuje się


(2.36)

Znaczy to, że jednostką indukcyjności jest jeden henr lub jedna omosekunda.

W rozpatrywanych w tym rozdziale obwodach, w stanach ustalonych natężenie prądu ma wartość stałą. Zatem w tego typu obwodach zjawisko samoindukcji może wystąpić jedynie w stanach przejściowych, czyli podczas zamykania lub otwierania obwodów. Aby to zjawisko zaistniało, odbiornik oprócz rezystancji musi zawierać również indukcyjność, np. cewkę z rdzeniem ferromagnetycznym. Niżej zostaną rozpatrzone dokładniej właśnie te dwa przypadki występowania zjawiska samoindukcji.

Przypadek I

Zamykanie obwodu składającego się z cewki o rezystancji R i indukcyjności L, nawiniętej na żelaznym rdzeniu.

W obwodzie jak na rys.2.18a, w chwili zamykania obwodu, natężenie prądu wzrasta od wartości zerowej do wartości
. W obwodzie indukuje się SEM samoindukcji


[V]

która posiada kierunek przeciwny do kierunku prądu i przeciwdziała jego narastaniu. W takiej sytuacji prąd nie od razu osiągnie wartość ustaloną. Jego wartość będzie zmieniała się w czasie, według krzywej
, opisanej zależnością


(2.37)

przy czym
nazywa się stałą czasową rozpatrywanego obwodu prądowego.




Rys.2.18. Zjawisko samoindukcji występujące przy zamykaniu obwodu elektrycznego prądu stałego: a) - schemat obwodu, b) - przebieg czasowy prądu

Z rys.2.18b wynika, że natężenie prądu dąży asymptotycznie do wartości ustalonej
. Przyjmuje się, że prąd w obwodzie osiąga wartość ustaloną po upływie czasu
. Rzeczywiście, po upływie czasu
wyrażenie
= 0,007, czyli natężenie prądu będzie się różniło od wartości ustalonej o 0,7%.

Z powyższych rozważań wynika wniosek, że im większa stała czasowa, tym później natężenie prądu osiągnie wartość ustaloną i odwrotnie.

Przypadek II

Otwieranie obwodu składającego się z cewki o rezystancji R i indukcyjności L, nawiniętej na żelaznym rdzeniu

Schemat obwodu i przebieg czasowy prądu przy rozwieraniu obwodu przedstawiono na rys.2.19. W tym przypadku kierunek SEM samoindukcji
jest zgodny z kierunkiem prądu, bowiem SEM przeciwdziała zanikaniu prądu. Zatem natężenie prądu nie od razu osiągnie wartość równą zeru, lecz będzie się zmieniało według krzywej, opisanej zależnością


(2.38)




Rys.2.19. Zjawisko samoindukcji występujące przy otwieraniu obwodu elektrycznego prądu stałego: a) - schemat obwodu, b) - przebieg czasowy prądu

Przy dużych wartościach indukcyjności (cewka z rdzeniem z ferromagnetyka o dużej przenikalności magnetycznej), wartość indukowanej SEM
też jest duża. Może to spowodować przebicie izolacji uzwojenia cewki oraz wypalenie zestyku (między biegunami wyłącznika tworzy się łuk elektryczny). Dlatego też przy otwieraniu obwodów z dużymi indukcyjnościami, zwiera się jednocześnie obwód za pomocą tzw. styku opalnego (rys.2.18a). Wytworzone przez cewkę pole magnetyczne zanika jednocześnie z prądem, płynącym w zwartym obwodzie, opisanym zależnością (2.38). Podobnie jak przy zamykaniu obwodu prądowego z indukcyjnością, przy jego otwieraniu czas trwania procesu przejściowego zanikania prądu również zależy od wielkości stałej czasowej, a proces można uważać za zakończony, po upływie czasu równego pięciu stałym czasowym.

Przykład 2.6

Obliczyć indukcyjność L₀ cewki bez rdzenia magnetycznego, mającej kształt pierścienia toroidalnego jak na rys.2.7. Średnica pierścienia, odpowiadająca średniej długości linii sił pola magnetycznego wewnątrz pierścienia
m, przekrój pierścienia
m², a liczba zwojów
.

Rozwiązanie

Indukcyjność cewki oblicza się z zależności (2.35)




Ponieważ strumień magnetyczny zamyka się przez powietrze, to
, bowiem przenikalność względną powietrza przyjmuje się
.

Średnia długość drogi strumienia magnetycznego w pierścieniu wynosi




Podstawiając wartości liczbowe do (2.35), otrzymuje się




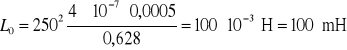
Przykład 2.7

Cewka o kształcie, wymiarach i liczbie zwojów jak w przykładzie 2.6 jest nawinięta na rdzeniu wykonanym z blachy twornikowej. Obliczyć indukcyjność cewki L oraz względną przenikalność magnetyczną rdzenia dla następujących wartości prądu w cewce: 0,5 A, 2,5 A, 5 A, 10 A i 15 A.

Rozwiązanie

Indukcyjność cewki oblicza się z zależności jak dla cewki bez rdzenia




Obliczenia indukcyjności cewki z rdzeniem różnią się od obliczeń indukcyjności cewki bez rdzenia tylko tym, że przenikalność magnetyczna ośrodka
, lecz jest znacznie większa i zmienia się w zależności od natężenia pola magnetycznego. W związku z tym można napisać, że
. Ponieważ
, to przenikalność względna ośrodka
. Natężenie pola magnetycznego obliczą się z wzoru
, zaś związek natężenia pola z indukcją ma postać
. Uwzględniając powyższe otrzymuje się
. Obliczając wartości natężenia pola magnetycznego dla poszczególnych wartości prądu i odczytując z krzywej magnesowania
blachy twornikowej (rys.2.9), odpowiadające im wartości indukcji magnetycznej, można obliczyć zależność
oraz L od prądu płynącego w cewce. Obliczone wartości wygodnie jest zestawić w tabeli.

Tabela 2.1. Wyniki obliczeń przenikalności magnetycznej względnej
i indukcyjności L dla wartości prądu, jak w przykładzie 2.7

Natężenie prądu I [A]	Natężenie pola H [ ]	Indukcja magnetyczna B [T]	Przenikalność magn. względna [-]	Indukcyjność [mH]
0,5	200	0,78	3100	310
1,5	600	1,15	1525	152
2,5	995	1,3	1040	104
5,0	1990	1,47	588	58,8
15	5979	1,68	224	22,4

Otrzymane wyniki obliczeń świadczą o tym, że zarówno przenikalność magnetyczna względna
, jak i indukcyjność L cewki z rdzeniem, zmniejszają się w miarę wzrostu prądu płynącego w cewce. Chcąc zwiększyć indukcyjność cewki należałoby zastosować rdzeń z ferromagnetyka o większej względnej przenikalności magnetycznej, ponieważ uzyskuje się wtedy mniejsze natężenie pola magnetycznego (mniejsze nasycenie rdzenia). Analogiczny rezultat można uzyskać zwiększając liczbę zwojów cewki z. Indukcyjność zwiększa się, ponieważ jest proporcjonalna do kwadratu liczby zwojów.

Zadanie można rozwiązać również inną metodą, a mianowicie obliczać indukcyjność z wzoru
. Wtedy należałoby dla każdej wartości prądu I obliczać z wzoru
wartość natężenia pola magnetycznego, odczytywać z krzywej magnesowania
materiału rdzenia wartości indukcji magnetycznej, odpowiadające obliczonym wartościom H, po czym obliczać wartości strumienia magnetycznego z wzoru
, gdzie S jest powierzchnią, przez którą przenika strumień.

2.9. Indukcja wzajemna

Na rys.2.20 przedstawiono dwa położone blisko siebie obwody 1 i 2. W obwodzie 1 płynie prąd elektryczny I₁ i wytwarza strumień Φ₁ . Strumień ten składa się z dwóch części (posiada dwie składowe)
i
, przy czym
+
. Strumień
jest skojarzony tylko z obwodem 1 i nie jest skojarzony z obwodem 2 (nie przenika przez niego). Strumień ten nazywa się strumieniem rozproszenia.




Rys.2.20. Rysunek wyjaśniający zjawisko indukcyjności wzajemnej

Strumień
jest skojarzony zarówno z obwodem 1 jak i 2. Zmiana w elementarnym czasie dt natężenia prądu o
w 1 obwodzie, spowoduje zmianę strumienia
, skojarzonego z obwodem 2 o
. Ta z kolei zmiana strumienia spowoduje wytworzenie w obwodzie 2 SEM indukowanej
, której wartość oblicza się z analogicznego jak dla indukcji własnej wzoru


(2.39)

Ponieważ strumień
zamyka się przez powietrze, to jest on proporcjonalny do prądu
, a więc i przyrost tego strumienia
jest proporcjonalny do prądu
, tj.


(2.40)

Z zależności (2.39), (2.40) otrzymuje się na SEM indukowaną
w postaci


(2.41)

Współczynnik proporcjonalności M, występujący w wzorach (2.39)÷(2.41) nazywa się indukcyjnością wzajemną.

Zjawisko powstawania w obwodzie siły elektromotorycznej indukowanej w wyniku zmian prądu w innym obwodzie, nazywa się indukcyjnością wzajemną.

Jednostkę indukcyjności wzajemnej można określić z zależności (2.40) i (2.41). Otrzymuje się wtedy, że


(2.42)

czyli, że jednostką indukcyjności wzajemnej, podobnie jak indukcji własnej, jest 1 henr.

Zjawisko indukcji wzajemnej znalazło zastosowanie w transformatorach, o czym będzie mowa w przedmiocie Maszyny Elektryczne.

1. Prądy wirowe

Jeżeli w jednorodnym polu magnetycznym poruszać płytę metalową tak, jak to przedstawiono na rys.2.21, to w elementarnych odcinkach tej płyty zaindukują się siły elektromotoryczne e, o kierunku, który można określić za pomocą reguły prawej dłoni. Pod wpływem tych SEM w płycie płyną prądy i, które zamykają się po drogach o najmniejszej rezystancji (patrz rys.2.21). Ponieważ drogi tych prądów przypominają wiry, prądy te nazwano prądami wirowymi (w fizyce zwane prądami Foucaulta).




Rys.2.21. Prądy wirowe

Wzajemne oddziaływanie prądów wirowych i strumienia magnetycznego Φ, powoduje powstawanie siły mechanicznej, działającej na płytę. Kierunek działania tej siły można określić na podstawie reguły lewej dłoni. Jak wynika z rysunku 2.21, kierunek ten jest przeciwny do kierunku ruchu płytki, czyli że siła ta hamuje poruszającą się płytę. Zjawisko to znalazło zastosowanie w hamulcach elektromagnetycznych, przyrządach pomiarowych (np. hamowanie tarczy konwencjonalnego licznika energii elektrycznej) itp. W wielu urządzeniach (wszystkie maszyny elektryczne) zjawisko to jest szkodliwe, powoduje bowiem straty energii, która wydziela się w rdzeniach magnetycznych w postaci ciepła.

Gdyby rdzenie ruchomych części maszyn elektrycznych wirujących były zbudowane z litego materiału, to podczas wirowania w polu magnetycznym powstawały by w nich prądy wirowe, zamykające się po drogach o najmniejszej rezystancji tak, jak to przedstawiono na rys.2.22a. Ponieważ rezystancja metalowego litego rdzenia jest bardzo mała, to prądy te osiągałyby duże wartości i powodowałyby duże straty.




Rys.2.22. Prądy wirowe w rdzeniu magnetycznym wirujących części maszyn elektrycznych: a) - w rdzeniu z litego materiału, b) - rdzeń pakietowany

Istnieją dwie możliwości ograniczenie tych prądów: pierwszy to zwiększyć rezystywność materiału rdzenia, drugi to wydłużyć drogę prądów wirowych w rdzeniu. Obydwa te sposoby są wykorzystywane w praktyce. Wykorzystanie pierwszego ze sposobów polega na budowaniu rdzeni magnetycznych ze stali o zwiększonej zawartości krzemu (do 4%). Zwiększa to rezystywność żelaza. Drugi możliwość jest realizowana poprzez budowanie rdzeni magnetycznych nie z litego materiału, lecz z pakietu blach (również o zwiększonej zawartości krzemu) odizolowanych od siebie specjalnym lakierem tak, jak to przedstawiono na rys.2.22b. Grubość blach wynosi (0,3÷0,4) mm - zwykle 0,35mm. Prądy wirowe muszą się wtedy zamykać w każdej z blach, przez co ich droga w żelazie jest dłuższa.

Rdzenie magnetyczne transformatorów, mimo braku ruchu rdzenia w polu magnetycznym, są również zbudowane z pakietów blach. Wynika to z faktu, że strumień magnetyczny w transformatorach jest zmienny w czasie, co również jest przyczyną powstawania prądów wirowych.




Rys.2.23. Pakietowany rdzeń transformatora

Warstwy izolacyjne w rdzeniu są równoległe do linii sił pola magnetycznego, tj. są prostopadłe do kierunku prądów wirowych, analogicznie jak w rdzeniach magnetycznych maszyn wirujących (porównaj rysunki 2.22a i 2.23). Skutek ograniczenia strat energii też jest analogiczny.

2. Energia pola magnetycznego

Prąd, płynący w obwodzie prądu stałego, wytwarza w elementach, które posiadają indukcyjność L, pole magnetyczne. Podczas wytwarzania tego pola prąd elektryczny wykonuje pewną pracę, która przekształca się w energię pola magnetycznego. Z poprzednich rozdziałów wiadomo, że praca prądu elektrycznego
[J] lub [Ws].

Narastający w procesie wytwarzania pola magnetycznego prąd elektryczny zmienia się w czasie i w elementarnym przyroście czasu
wykonuje pracę


(2.43)

przy czym u jest napięciem na cewce o indukcyjności L.

Z rozdziału 2.9 wiadomo, że w cewce z narastającym prądem indukuje się siła elektromotoryczna samoindukcji, która zgodnie z regułą Lenza, przeciwdziała narastaniu prądu, a więc jest skierowana przeciwnie do przyłożonego napięcia (prąd ma ten sam kierunek co napięcie, ponieważ jest wymuszony przez napięcie), czyli


(2.44)

Z zależności (2.43) i (2.44) wynika, że




co po podstawieniu
daje


(2.45)

przy czym
jest przyrostem energii pola magnetycznego, odpowiadającym przyrostowi prądu
.

Całkowita energia, zgromadzona w polu magnetycznym podczas narastania prądu od zera do wartości ustalonej I, jest równa pracy wykonanej przez prąd elektryczny. W celu określenia wartości tej pracy należy scałkować równanie (2.45). Otrzymuje się wtedy


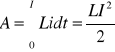
(2.46)

przy czym jeżeli L jest indukcyjnością obwodu w henrach, a I wartością ustaloną natężenia prądu w amperach, to wynik otrzymuje się w watosekundach (dżulach).

Po rozwarciu obwodu z indukcyjnością, prąd elektryczny zanika od wartości ustalonej do zera, a energia nagromadzona w polu magnetycznym wraca do źródła.

Końcowa postać wyrażenia na energię zgromadzoną w polu magnetycznym przypomina znaną z mechaniki zależność na energię kinetyczną, tj.




w której m jest masą poruszającego się ciała, a v prędkością liniową tego ciała.

Uwaga:

W rozważaniach niniejszego rozdziału założono, że obwód elektryczny jest idealny, to znaczy że zawiera on tylko indukcyjność, a jego rezystancja jest równa zeru.

---