16. Jakość liniowych układów automatycznej regulacji

W wyniku oddziaływania na układ regulacji zakłóceń lub wymuszenia (zmiany wartości zadanej) powstaje, w zależności od charakteru oddziaływań i właściwości układu regulacji, przejściowa lub trwała odchyłka regulacji. Zadaniem układu automatycznej regulacji jest działanie zmierzające do zmniejszania tej odchyłki. Jak wykazano w rozdziale poprzednim, działanie takie realizować mogą tylko układy stabilne asymptotycznie. Układ stabilny asymptotycznie, po ustaniu oddziaływania wytrącającego go ze stanu równowagi, wraca do początkowego stanu równowagi. Jednakże nawet układ stabilny asymptotycznie może okazać się nieużyteczny jeżeli np. czas osiągania stanu równowagi byłby bardzo długi lub osiągany po wykonaniu wielu wahań o znacznej amplitudzie. Dlatego oprócz wymogu stabilności asymptotycznej układom regulacji stawiane są dodatkowe wymagania, ogólnie określane jako wymagania dotyczące jakości układu regulacji. Określają one wymagane zachowanie się układu w stanach przejściowych - bezpośrednio po zmianie wartości zadanej albo po pojawieniu się lub zaniku zakłócenia oraz w stanach ustalonych - po ustaniu procesów przejściowych.

Wymagania dotyczące przebiegu procesów przejściowych w układach regulacji określane są za pomocą szeregu wskaźników, nazywanych ogólnie wskaźnikami jakości dynamicznej układu regulacji.

Jakość regulacji w stanach ustalonych nazywa się ogólnie dokładnością statyczną układu regulacji.

Dalsze rozważania dotyczące jakości układów i wyprowadzone zależności odnoszą się tylko do układów regulacji stabilnych asymptotycznie.

W rzeczywistym układzie regulacji odchyłka regulacji
w danej chwili
może być sumą dwóch składowych:

• odchyłki
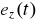
  wywołanej działaniem zakłócenia (odchyłki zakłóceniowej),

• odchyłki
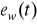
  wywołanej działaniem wymuszenia (odchyłki nadążania).

A więc

(16.1)

Przy ocenie jakości układu regulacji analizuje się oddzielnie obie składniki odchyłki.

Odchyłkę regulacji definiuje się jako różnicę między bieżącą wartością wielkości regulowanej i wartością zadaną

(16.2)

Do wyznaczenia odchyłek regulacji posłużmy się uproszczonym schematem układu regulacji - rys. 16.1.

Rys. 16.1. Uproszczony schemat układu regulacji automatycznej

Wyznaczmy odchyłkę zakłóceniową
, spowodowaną działaniem zakłócenia
na układ, przyjmując jako początkowy stan układu
,
, co oznacza, że w stanie początkowym
.

Wprowadzenie zakłócenia
przy
wywoła zmianę wielkości regulowanej o wartość
i powstanie odchyłki regulacji

Na podstawie rys. 10.1 można napisać:

(16.3)

Wykonując odwrotne przekształcenie Laplace'a można wyznaczyć funkcję
.

(16.4)

Stosunek
nazywany jest transmitancją odchyłkową układu względem zakłócenia

(16.5)

Wyznaczmy odchyłkę nadążania
, spowodowaną zmianą wartości zadanej
, przyjmując jako początkowy stan układu
,
, co oznacza, że w stanie początkowym
.

Zmiana wartości zadanej
przy
, wywoła zmianę
wielkości regulowanej

i powstanie odchyłki regulacji

Transformatę tej odchyłki można wyznaczyć bezpośrednio na podstawie przekształconego schematu blokowego układu z rys. 16.1 - rys. 16.2, w którym jako wielkość wyjściową potraktowano ujemną wartość odchyłki regulacji.

Rys. 16.2. Przekształcony schemat układu z rys. 16.1

(16.6)

Wykonując odwrotne przekształcenie Laplace'a można wyznaczyć funkcję
.

(16.7)

Stosunek
nazywany jest transmitancją odchyłkową układu względem wartości zadanej

(16.8)

16.1. Dokładność statyczna liniowych układów regulacji

Dokładność statyczną określają występujące w stanach ustalonych różnice między wielkością regulowaną a wartością zadaną, zwane odchyłkami statycznymi.

Wartości odchyłek regulacji osiągane po wprowadzeniu zakłócenia
lub wymuszenia
i po zaniku procesów przejściowych - odchyłek statycznych
i
, wyznaczać można na podstawie wzorów (16.3) i (16.6), korzystając z twierdzenia (2.13 )

o wartości końcowej:

(16.9)

oraz

(16.10)

Wzory (16.9) i (16.10) umożliwiają przeprowadzenie oceny wpływu właściwości obiektu i regulatora na wartość odchyłek statycznych.

Dla układów regulacji stałowartościowej wymagania dotyczące dokładności statycznej ogranicza się zwykle do określenia wartości odchyłek statycznych dla zakłóceń lub wymuszeń o stałej wartości. Formułowane są one w postaci dopuszczalnych wartości odchyłek statycznych, wyrażonych w jednostkach wielkości regulowanej lub częściej jako wyrażony w procentach:

• w przypadku odchyłki zakłóceniowej - stosunek maksymalnej wartości odchyłki
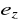
  do maksymalnej wartości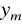
  

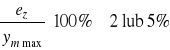
, (16.11)

• w przypadku odchyłki nadążania - stosunek maksymalnej wartości odchyłki
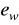
  do maksymalnej wartości zadanej

(16.12)

W przypadku układów nadążnych, w zależności od potrzeby, wymagania dotyczące dokładności statycznej mogą obejmować także odchyłki statyczne występujące podczas oddziaływań liniowo narastających i innych.

Przykład 16.1

Wyznaczyć odchyłki statyczne w układzie regulacji stałowartościowej, pokazanym na rys. 16.3, wywołane zakłóceniem
i zmianą wartości zadanej
w przypadku zastosowania:

1. regulatora P,

2. regulatora PD,

3. regulatora PI.

Rys.16.3. Schemat blokowy do przykładu 16.1

Rozwiązanie

Porównując rozważany układ ze schematem na rys. 16.1 można stwierdzić, że

,

W przypadku a) transmitancja regulatora ma postać

Zatem:

- odchyłka statyczna wywołana zakłóceniem
jest równa

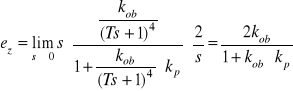
- odchyłka statyczna wywołana zmianą wartości zadanej
wynosi

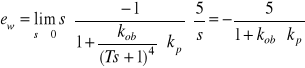
W przypadku b) transmitancja regulatora ma postać

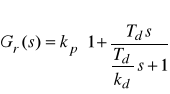
A więc:

- odchyłka statyczna wywołana zakłóceniem
jest równa

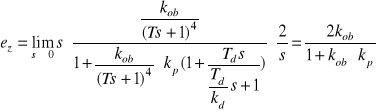
- odchyłka statyczna wywołana zmianą wartości zadanej
wynosi

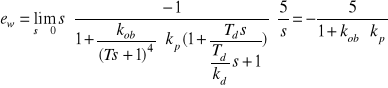
W przypadku c) transmitancja regulatora ma postać

A więc

- odchyłka statyczna wywołana zakłóceniem
jest równa

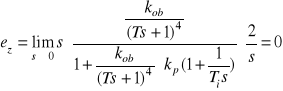
- odchyłka statyczna wywołana zmianą wartości zadanej
wynosi

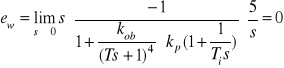
Otrzymane wyniki pozwalają na sformułowanie następujących wniosków:

1. W układzie z obiektem statycznym i regulatorem o algorytmie P lub PD występują niezerowe odchyłki statyczne zarówno zakłóceniowe jak i nadążania proporcjonalne odpowiednio do wartości zakłócenia lub zmiany wartości zadanej.

2. Zwiększenie wzmocnienia proporcjonalnego regulatora P lub PD zmniejsza wartość odchyłek statycznych. Zmniejszenie odchyłki statycznej przez zwiększenie wzmocnienia jest zwykle ograniczone ze względu na warunki stabilności układu. (Układ z regulatorem PD osiąga granicę stabilności przy większym wzmocnieniu regulatora niż w przypadku układu z regulatorem P.)

3. Akcja całkująca występująca w regulatorze zapewnia zerowe odchyłki statyczne przy stałych wartościach zakłócenia lub stałych zmianach wartości zadanej

Wykorzystując wzór (16.10) można wykazać, że w układzie z regulatorem P i obiektem regulacji z akcją całkowania, statyczna odchyłka nadążania także jest równa zero.

Układy regulacji, w których występują niezerowe odchyłki statyczne wywołane oddziaływaniem zakłóceń lub wymuszeń o stałej wartości, nazywają się układami statycznymi; układy, w których pomimo oddziaływania zakłóceń lub wymuszeń o stałej wartości występują zerowe odchyłki statyczne, nazywają się układami astatycznymi pierwszego rzędu.

Astatycznymi drugiego rzędu nazywają się układy posiadające tę właściwość, że wykazują zerowe odchyłki statyczne nawet w przypadku istnienia zakłóceń lub zmian wartości zadanej przebiegających w sposób liniowo narastający.

W rzeczywistych układach regulacji mimo działania całkującego regulatora występuje pewna wartość odchyłki statycznej. Wynika to z niedokładności regulatora niedokładności pozostałego sprzętu automatyki, głównie przetwornika pomiarowego.

16.2. Jakość dynamiczna

Jakość dynamiczną ocenia się za pomocą szeregu wskaźników, do których należą:

• wskaźniki określające parametry przebiegu odchyłek regulacji po wprowadzeniu skokowego zakłócenia lub skokowej zmiany wartości zadanej (tzw. wskaźniki przebiegu przejściowego),

• wskaźniki częstotliwościowe,

• całkowe wskaźniki jakości.

16.2.1. Wskaźniki przebiegu przejściowego

Podstawową formą oceny właściwości dynamicznych układu regulacji jest ocena przebiegów odchyłek regulacji wywołanych przez zakłócenie skokowe lub skokową zmianą wartości zadanej. Charakterystyczne postacie takich przebiegów przedstawiono na rys. 16.4 - 16.7. Do oceny tych przebiegów najczęściej wykorzystywane są następujące wskaźniki:

• statyczna odchyłka zakłóceniowa
  ,

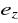
• statyczna odchyłka nadążania
  ,

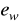
• maksymalna odchyłka dynamiczna
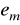
  - maksymalna wartość odchyłki regulacji po wprowadzeniu zakłócenia skokowego lub skokowej zmiany wartości zadanej,

• czas regulacji
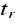
  - czas od chwili wprowadzenia skokowego zakłócenia lub wymuszenia do chwili, od której odchyłka regulacji nie wykracza poza przedział wartości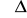
  od wartości odpowiednio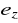
  lub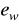
  ; jako wartość
  przyjmuje się najczęściej 2% lub 5% wartości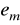
  ,

• przeregulowanie
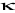
  (dotyczy przebiegów periodycznych) - wyrażony w procentach stosunek amplitudy drugiego odchylenia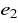
  od wartości ustalonej do amplitudy pierwszego odchylenia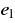
  

(16.13)

Wartości wymienionych wskaźników przebiegu przejściowego zależą od właściwości obiektu regulacji, zastosowanego algorytmu regulacji i nastaw regulatora.

Z punktu widzenia użytkownika, ze względu na możliwość oceny przebiegu realizowanego procesu, poza wartościami odchyłek regulacji ważne są wartości wielkości regulowanej zarówno w stanach ustalonych jak i przejściowych. Dlatego na rysunkach ilustrujących charakterystyczne rodzaje odpowiedzi skokowych układów regulacji pokazano równolegle przebieg wielkości regulowanej i odpowiadający mu przebieg odchyłki regulacji.

Charakterystycznymi odpowiedziami skokowymi układu regulacji są:

• odpowiedzi na zakłócenie skokowe:

- periodyczne (oscylacyjne):

- o niezerowej odchyłce statycznej (układ z regulatorem P lub PD) - rys. 16.4a,

- o zerowej odchyłce statycznej (układ z regulatorem PI lub PID) - rys. 16.4b,

- aperiodyczne
- o niezerowej odchyłce statycznej (układ z regulatorem P lub PD) - rys. 16.5a,

- o zerowej odchyłce statycznej (układ z regulatorem PI lub PID) - rys. 16.5b,

• odpowiedzi na skokową zmianę wartości zadanej:

- periodyczne (oscylacyjne):

- o niezerowej odchyłce statycznej (układ z regulatorem P lub PD) - rys. 16.6a,

- o zerowej odchyłce statycznej (układ z regulatorem PI lub PID lub z obiektem z akcją całkującą) - rys. 16.6b,

- aperiodyczne
- o niezerowej odchyłce statycznej (układ z regulatorem P lub PD) - rys. 16.7a,

- o zerowej odchyłce statycznej (układ z regulatorem PI lub PID lub z obiektem z akcją całkującą) - rys. 16.7b,

a)

b)

Rys. 16.4. Oscylacyjne odpowiedzi układu regulacji na zakłócenie skokowe
przy
: a) z niezerową odchyłką statyczną, b) z zerową odchyłką statyczną

a)

b)

Rys. 16.5. Aperiodyczne odpowiedzi układu regulacji na zakłócenie skokowe
przy
: a) z niezerową odchyłką statyczną, b) z zerową odchyłką statyczną

a)

b)

Rys. 16.6. Oscylacyjne odpowiedzi układu regulacji na skokową zmianę wartości zadanej
przy
: a) z niezerową odchyłką statyczną, b) z zerową odchyłką statyczną

a)

b)

Rys. 16.7. Aperiodyczne odpowiedzi układu regulacji na skokową zmianę wartości zadanej
przy
: a) z niezerową odchyłką statyczną, b) z zerową odchyłką statyczną

Przebiegi aperiodyczne charakteryzują się najkrótszymi czasami regulacji ale jednocześnie największymi dynamicznymi odchyłkami regulacji.

Wpływ rodzaju regulatora na przebieg (aperiodyczny) odchyłki regulacji po wprowadzeniu zakłócenia skokowego
przy
ilustruje rys. 16.8.

Rys. 16.8. Wpływ rodzaju regulatora na przebieg (aperiodyczny) odchyłki regulacji po wprowadzeniu zakłócenia skokowego
przy
: 1 - układ z regulatorem P, 2 - układ z regulatorem PI, 3 - układ z regulatorem PID

W układzie regulacji z regulatorem o algorytmie P obserwuje się najszybszą kompensację wpływu zakłócenia (najkrótszy czas regulacji
) ale regulacja jest najmniej dokładna gdyż odchyłka statyczna
; odchyłka dynamiczna
ma także wartość największą. W układzie z regulatorem o algorytmie PI lub PID odchyłki statyczne są zerowe, odchyłki dynamiczne są mniejsze od odchyłek w układzie z regulatorem P, przy czym odchyłka dynamiczna jest najmniejsza w przypadku zastosowania regulatora o algorytmie PID.

Wpływ nastaw regulatora P na kształtowanie się odchyłki regulacji po wprowadzeniu zakłócenia skokowego
przy
ilustruje rys. 16.9. Aperiodyczny przebieg odchyłki odpowiada wzmocnieniu
regulatora, przy którym odchyłka statyczna osiąga wartość
. Jak wiadomo, zwiększanie wzmocnienia regulatora prowadzi do zmniejszenia odchyłki statycznej. Zwiększanie wzmocnienia regulatora prowadzi do zmiany charakteru przebiegu odchyłki na przebieg oscylacyjny; dalsze zwiększanie wzmocnienia regulatora mogłoby doprowadzić do oscylacji niegasnących i utraty stabilności.

Rys. 16.9. Wpływ nastaw regulatora P na kształtowanie się odchyłki regulacji po wprowadzeniu zakłócenia skokowego
przy

Jak widać z porównania przebiegów przejściowych na rys. 16.9, przebiegi oscylacyjne charakteryzują się mniejszą odchyłką dynamiczną (
), mniejszą odchyłką statyczną (
) ale dłuższym czasem regulacji (
).

W praktyce zaobserwowano związki pomiędzy zapasami stabilności a reakcją układu na zakłócenie skokowe. Stwierdza się, że zapewniając zapasy stabilności w granicach:

lub

oraz

w większości układów regulacji, po wprowadzeniu zakłócenia skokowego, przebiegi przejściowe mają charakter oscylacyjny z minimum czasu regulacji i przeregulowaniem około 20 %.

16.2.2. Całkowe wskaźniki jakości regulacji

Ocena jakości regulacji na podstawie parametrów przebiegu przejściowego ma tę wadę, że ich sprawdzenie w układzie wymaga dużego nakładu pracy obliczeniowej, podczas gdy warunki eksploatacji układu z reguły nie tylko nie narzucają ściśle określonych wartości tych parametrów, ale nawet nie ustalają sygnału skokowego jako głównie miarodajnego. Z tych też względów stosuje się do oceny jakości dynamicznej pośrednich metod oceny jakimi są oceny całkowe, które są często łatwiejsze w obliczeniach i umożliwiają w pewien sposób ocenę całego przebiegu przejściowego, a nie jednego z jego odrębnych parametrów.

Miarą jakości regulacji może być wielkość pola pod krzywą odchyłki regulacji. Dąży się do minimalizacji tego pola. Im mniejsze jest to pole, tym lepsza jest jakość dynamiczna układu. Podejście takie ma również interpretację ekonomiczną, gdyż często straty energii lub materiału (surowca)w procesach produkcyjnych są funkcją wielkości i czasu trwania odchyłki regulacji, a celem regulacji jest minimalizacja tych strat.

Zależnie od struktury i parametrów układu regulacji oraz spodziewanego charakteru przebiegu przejściowego oblicza się wartości następujących całek:

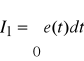
(16.17)

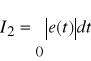
(16.18)

 
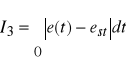
(16.19)

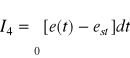
(16.20)

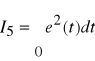
(16.21)

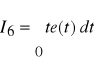
(16.22)

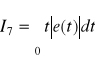
(16.23)

Całkową miarą jakości układów statycznych regulacji (odchyłka statyczna nie jest zerowa) w przypadku przebiegów oscylacyjnych jest minimum całki I₃ , dla przebiegów aperiodycznych minimum całki I_4. Dla układów astatycznych całkową miarą jakości są całki I₁ dla przebiegu aperiodycznego i I₂ dla przebiegu oscylacyjnego.

W przypadku układów dla których wymagania odnośnie jakości formułowane są tak aby uzyskać jak najmniejsze wahania wielkości regulowanej oraz układów czasooptymalnych minimalizuje się następujące całki : I₅ , I₆, I₇.

Dla typowych układów regulacji, zapewnienie minimalnej wartości całki I₂ prowadzi dla zakłóceń skokowych do przebiegów aperiodycznych z minimum czasu regulacji, dla całki I₅ do przebiegów oscylacyjnych z przeregulowaniem
.

212

---