2. Prostowniki jednofazowe, jednokierunkowe, pełnosterowane, jednopulsowe 1T

Prostowniki jednofazowe jednopulsowe są najprostszymi układami prostowniczymi spotykanymi w praktyce. Ich prostota powoduje, że posiadają cechy niewygodne dla odbiorników (np. impulsowy charakter prądu) i sieci zasilającej (np. duże odkształcenie prądu sieci, występowanie składowej stałej itp.).

2.1. Praca prostownikowa

ε

Rys. 2.1. Schemat prostownika jednopulsowego 1T z obciążeniem RLE

Na schemacie zaznaczono źródło zasilania - sieć AC, posiadające napięcie,
;
, tyrystor, i odbiornik o charakterze RLE.

Do analizy przyjęto oznaczenia:

oraz ξ=arc sin
, przy czym

ξ < ϑ_z < π - ξ,

i założenia :

- sieć sztywna AC, co oznacza, że R_k=0 i L_k=0

- tyrystor idealny r_t = 0, r_r = ∞, r_d = ∞, gdzie:

r_t - rezystancja przewodzenia tyrystora;

r_r - rezystancja stanu zaporowego tyrystora;

r_d - rezystancja stanu blokowania (zatkania).

Dla prostowników ważne jest wyznaczenie parametrów:

- wartości chwilowych napięcia na odbiorniku u_d i prądu odbiornika i_d,

- wartości średniej napięcia na odbiorniku U_d i prądu odbiornika I_d,

- wartości maksymalnej napięcia na tyrystorze (tyrystorach) U_TM, wartości maksymalnej prądu tyrystora I_TM oraz wartości średniej prądu tyrystora I_TAV.

Obliczenie poszczególnych wielkości jest uzależnione od przepływu prądu przewodzenia tyrystora i odbiornika, dlatego też od tej wielkości zaczynamy analizę pracy prostownika. Wartość chwilową prądu odbiornika i tyrystora wyznaczyć można równania różniczkowego (2.1) określonego na podstawie II prawa Kirchhoffa dla wartości chwilowych napięć w obwodzie prostownika, dla stanu przewodzenia tyrystora.

(2.1)

gdzie:

Równanie (2.1) jest słuszne dla przedziału:

przy czym ξ≤
≤π- ξ

po przekształceniu równanie (2.1) przyjmie postać:

(2.2)

Z równania (2.2) można wyliczyć:

składową ustaloną

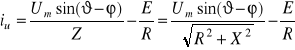
, (2.3)

gdzie: ϕ=arctg
a

i składową przejściową i_p, z równania charakterystycznego:
, po następujących przekształceniach:

-
;

-
;

-
;

-
;

-

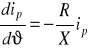
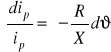
Wartość chwilowa prądu odbiornika (rozwiązanie ogólne) (a także sieci AC i tyrystora) wyniesie ostatecznie:

(2.4)

Rozwiązanie szczególne uzyskuje się po uwzględnienie warunków początkowych.

Warunki początkowe;

ϑ=ϑ_z, i=0

Dla tych warunków początkowych wylicza się:

stałą: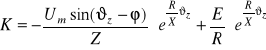
,

oraz przebieg prądu i w postaci:

(2.5)

lub
(2.6)

dla

gdzie:

Tyrystor wyłącza się po zaniku prądu
do zera. Aby obliczyć kąt gaśnięcia (wyłączenia) tyrystora należy funkcję i przyrównać do zera.

Rys. 2.2. Przebiegi napięć i prądów w prostowniku 1T przy obciążeniu RLE

Zależności na wartości chwilowe napięć na odbiorniku
, na tyrystorze

i prądu odbiornika
można zapisać:

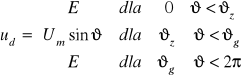
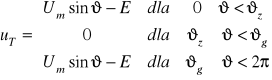
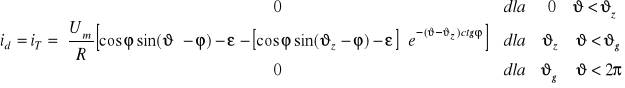
Poszukiwanie kąta granicznego przewodzenia tyrystora

Dla
,

Po przyrównaniu prądu i do zera dla
, otrzymamy równie wykładniczo-trygonometryczne:
, które po przekształceniach otrzymujemy w postaci:
. Stąd wyliczyć można kąt gaśnięcia
,
, przy czym wyrażenie to jest funkcją uwikłaną niemożliwą do rozwiązania metodami analitycznymi. Wartości kąta
odczytać można z wykresu:

Znając wartość kąta
można określić pozostałe poszukiwane parametry ważne z punktu widzenia pracy odbiornika i tyrystora:

- wartość średnią napięcia na odbiorniku
,

- wartość średnią prądu odbiornika
,

- wartość maksymalną napięcia na tyrystorze
,

- wartość średnia prądu tyrystora
.

Wartość średnia napięcia na odbiorniku wylicza się korzystając ze wzoru-definicji wartości średniej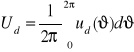
. Dla rozpatrywanego przypadku pracy prostownika 1T z obciążeniem RLE uzyskujemy:

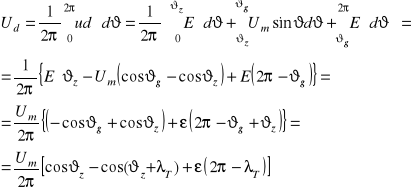
(2.7)

gdzie:

Dla składowych stałych napięć można posługiwać się schematem zastępczym:

Rys. 2.3. Schemat zastępczy prostownika 1T dla składowych stałych napięć

Na schemacie uwzględniono, że
, ponieważ pochodna wartości stałej prądu
,
a zatem i
, bowiem każda całka oznaczona (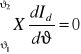
). Całka oznaczona z wartości 0 jest równa 0.

Ze schematu zastępczego dla składowych stałych wynika zależność
, stąd:

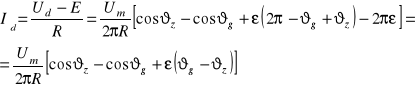
(2.8)

a
, wartość maksymalna napięcia na tyrystorze:

Uzyskane zależności dla prostownika 1T z obciążeniem RLE są przydane do obliczeń przy innych rodzajach obciążeń.

Przypadek
obc.RE ,

Wtedy: X=0,
,

a zakres sterowania dotyczyć będzie przedziału:

Poszukiwane zależności przyjmą postać:

- przebieg prądu odbiornika:
dla
, gdzie:
(2.9)

- wartość średnia napięcia na odbiorniku:
lub
, (2.10)

gdzie wprowadzono:
i
a

- wartość średnia prądu odbiornika:
, (2.11)

- wartość średnia prądu tyrystora:
, (2.12)

- wartość maksymalna napięcia na tyrystorze:
(2.13)

Rys. 2.4. Przebiegi napięć i prądów w prostowniku 1T, przy obciążeniu RE

Przypadek
, obc. RL

wtedy: E = 0, ε = 0,
,

a zakres sterowania dotyczyć będzie przedziału:

Poszukiwane wielkości i parametry i=i_d=i_T, U_d, I_d, U_TM określają zależności:

- przebieg prądu odbiornika:
lub ostatecznie

dla
(2.14)

- wartość średnia napięcia na odbiorniku:
, (2.15)

gdzie
należy odczytać z wykresu
;

- wartość średnia prądu odbiornika:
, (2.16)

- wartość średnia prądu tyrystora:
, (2.17)

- wartość maksymalna napięcia na tyrystorze:
, ponieważ E=0 (2.18)

Rys. 2.5. Przebiegi napięć i prądów w prostowniku 1T, przy obciążeniu RL

Przypadek
obc. R

Wtedy L=0 i E=0 a zatem także ε = 0,

a zakres sterowania dotyczyć będzie przedziału:

Poszukiwane wielkości i parametry
, określają zależności:

- przebieg prądu odbiornika:

, dla
(2.19)

- wartość średnia napięcia na odbiorniku:

(2.20)

- wartość średnia prądu odbiornika:
(2.21)

- wartość średnia prądu tyrystora:
(2.22)

- wartość maksymalna napięcia na tyrystorze:
(2.23)

Rys. 2.6.. Przebiegi napięć i prądów w prostowniku 1T, przy obciążeniu R

Ilustracją procesu sterowania w prostownikach tyrystorowych jest charakterystyka sterowania, zdefiniowana jak zależność wartości średniej napięcia wyprostowanego na odbiorniku od kąta sterowania:
. Do sporządzenia wykresów tej charakterystyki korzysta się najczęściej z zależności względnej średniego napięcia wyprostowanego na odbiorniku odniesionej do wartości tego napięcia obliczonego dla kąta sterowania równego
;
. Wówczas wartość względną napięcia wyprostowanego
określona jest zależnością:
a charakterystyka sterowania będzie funkcją kąta sterowania wyrażoną w następujący sposób:
.

Rys. 2.6. Charakterystyka sterowania prostownika 1T przy różnych rodzajach obciążenia
,

2.2. Praca falownikowa średnia w układzie jednopulsowym 1T.

Praca falownikowa średnia w prostowniku ma miejsce w prostowniku gdy moc składowych stałych
. Ponieważ prąd średni może przyjmować tylko wartości
, zatem przy pracy falownikowej średniej napięcie
. Jest to możliwe do uzyskania tylko wówczas gdy SEM w obwodzie odbiornika
.

Rys.2.7. Przebieg napięcia na odbiorniku prostownika 1T przy pracy falownikowej

Podsumowując praca falownikowa ma miejsce wtedy gdy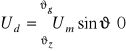

2.3.Układ jednopulsowy z diodą rozładowczą (zerową) 1T+1D

Rys. 2.8. Schemat układu jednopulsowego z diodą rozładowczą 1T+1D

Układy jednopulsowe z diodą rozładowczą stosowane są głównie wtedy gdy odbiornik zawiera bardzo dużą indukcyjność L. W takich przypadkach praca tylko tyrystora wiąże się z dość długim przedziałem pracy falownikowej chwilowej po przejściu napięcia zasilania przez 0 w punkcie
, bowiem kąt gaśnięcia wówczas
. Zastosowanie diody rozładowczej powoduje nie dopuszczenie układu do pracy falownikowej chwilowej
i w momencie
następuje jednoczesne wyłączenie tyrystora i załączenie diody D. Na odbiorniku zamiast ujemnego napięcia wystąpi niewielka pomijalna wartość napięcia na przewodzącej diodzie D. Tyrystor zaś zostaje zablokowany ujemnym napięciem zasilania.

Przyjmując uproszczenia (r_t = 0, r_r = ∞, r_d = ∞) w przedziale przewodzenia tyrystora
obwód w którym popłynie prąd można opisać równaniem dla wartości chwilowych napięć wynikającym z II prawa Kirchhoffa:

, zakładając, że

Ponieważ
,
,
, równanie to przyjmuje postać:

, przy czym w tym zakresie

Rozwiązaniem ogólnym tego równania jest suma składowych:

- ustalonej:
lub
, bowiem
a

- przejściowej:
, wyliczonej z rozwiązania równania charakterystycznego:
; .

Przebieg prądu
w przedziale przewodzenia tyrystora wyznacza się z sumy składowych ustalonej
i przejściowej jako
:

.

Stałą całkowania K wyznacza się z warunków początkowych:
, wstawionych do rozwiązania ogólnego:

.

nie jest znane, ma jednak wartość większą od zera, bowiem jest to wartość prądu odbiornika przejmowana przez tyrystor w chwili jego załączenia
.

Wstawiając K do rozwiązania ogólnego, otrzymujemy przebieg i_d w zakresie
, przewodzenia tyrystora T:

,
(2.24)

W momencie
napięcie zasilania AC zmienia wartość z dodatniej na ujemną, kończy przewodzić tyrystor zaczyna przewodzić dioda D. Odbiornik zwarty jest diodą zatem
.

Wówczas dla obwodu odbiornika równanie wyrażające przepływ prądu
, wynikające z II prawa Kirchoffa będzie następujące:

(2.25)

Rozwiązaniem ogólnym tego równania jest wyrażenie obejmujące składową przejściową prądu odbiornika.

(2.26)

Stałą A wyznacza się z warunków początkowych, odpowiadających rozpoczęciu przewodzenia przez diodę:
, wówczas
, stąd
. Ostatecznie rozwiązaniem równania 2.26) jest :

(2.27)

Wartości
oraz
można wyliczyć wstawiając
do równania (2.27) dla
a
do równania (2.24) - dla
, otrzymuje się układ równań algebraicznych:

(2.27)

(2.28)

Rozwiązaniem układu równań (2.27) i (2.28) jest:

(2.29)

Jeżeli X jest znacząco większe od R (X>>R) wówczas
i
, wtedy
.

Wartość średnią napięcia na odbiorniku oblicza się posługując przebiegiem tego napięcia (rys.2.9) w jednym okresie
:

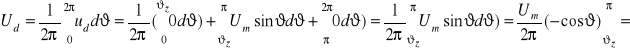
Ostatecznie:

(2.30)

Rys. 2.9. Przebiegi: napięcia na odbiorniku, prądu odbiornika i napięcia na tyrystorze w prostowniku 1T-1D; linia przerywana na wykresie oznacza przypadek gdyby wyłączono diodę

Charakterystykę sterowania
,

gdzie:
=
, wyznacza zależność:

(2.31)

oraz wykonany na jej podstawie wykres:

Rys.2.10. Charakterystyka sterowania prostownika 1T-1D

- wartość średnia prądu odbiornika:
; (2.32)

- wartość średnia prądu tyrystora obliczana jest zwykle z zależności przybliżonej:

(2.33)

a wartość średnia prądu diody:
; (2.34)

gdzie:

,

, (patrz rys.2.9)

- wartość maksymalna napięcia na tyrystorze:
. (2.35)

Rys. 2.10. Przebiegi napięcia na odbiorniku, prądu odbiornika, prądu tyrystora i prądu diody w prostowniku 1T-1D,dla odbiornika RL (RX), przy (X>>R)

Rys. 2.11. Przebieg napięcia na odbiorniku RLE w układzie 1T-1D; a) dla przypadku gdy
, b) dla przypadku gdy

W przypadku a) (rys.2.11)
w całym przedziale okresu
i dioda rozładowcza nie wchodzi w stan przewodzenia a prąd odbiornika ma charakter przerywany. W przypadku b) dioda przewodzi w przedziale
a prąd odbiornika ma charakter przerywany.

Dla przypadku b) kąt gaśnięcia diody
wyznaczyć można z zależności:

2.36

gdzie
to wartość prądu dla
, którą można wyliczyć korzystając ze wzoru (2.6), dla
, ponieważ prąd odbiornika jest przerywany i tyrystor po załączeniu rozpoczyna przewodzenie od wartości 0:

2.37

a dla

2.38

55

---