1Wszystkie obliczenia sporządziłem na podstawie danych z roku 1999. Dane te wraz z obliczeniami dołączone są jako załącznik do niniejszego projektu na jego końcu.

Zadaniem w tej części jest opracowanie statystyczne i interpretacja wyników dotyczące ładunku BZT₅ i CHZT w ściekach dopływających do oczyszczalni ścieków „Czajka” z Żerania.

Otrzymane dane przedstawiają pomiary uporządkowane w szereg statystyczny wyliczający, stąd wszystkie zastosowane wzory odnoszą się do takiego właśnie szeregu.

Na wstępie sporządziłem dwa wykresy (Rys.1.1 i Rys.1.2), oddzielnie dla BZT5 i CHZT, aby lepiej poznać rozkład ładunków w czasie. Wykresy te załączone są na końcu projektu. Graficzna metoda przedstawienia tego rozkładu jest przejrzysta i pozwala na szybką ocenę skali zjawiska, jego zmienności czy niezmienności.

Sporządziłem również histogramy (Rys.1.3 i Rys1.4) na podstawie których można stwierdzić, czy rozkład jest jednomodalny, czy jest symetryczny.

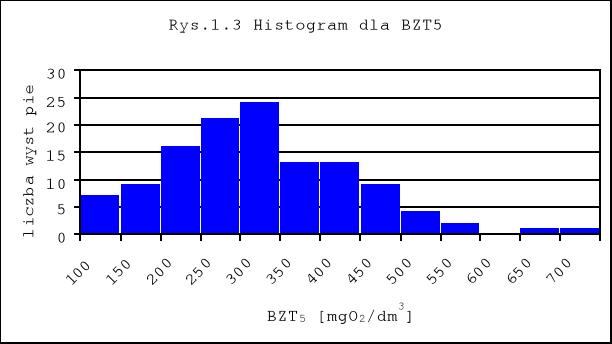
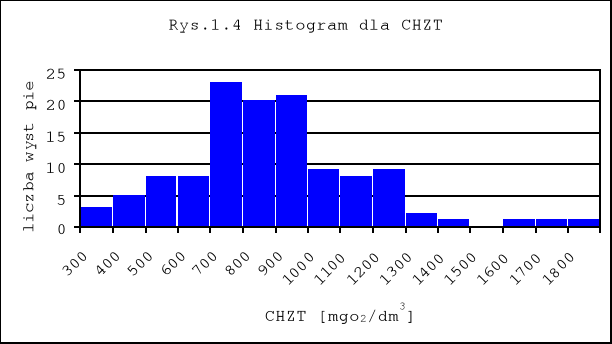
Dzięki ww. graficznym obrazom rozłożenia ładunków łatwiej można wychwycić jakieś wyjątkowe, odstające od normy, sytuacje, które miały miejsce w badanym okresie:

• 18.12.99 - zarówno BZT₅ jak i CHZT są na bardzo wysokim poziomie, a wielkość przepływu tego dnia jest mała;

• 14.01.99 - duży wzrost BZT₅ i szybki spadek do średniej już po dwóch dniach;

• 08.07-02.08 - mała wartość BZT₅;

• 08.07-29.07 - mała wartość CHZT.

• 19.04-20.05 - długi i duży spadek BZT₅;

Na podstawie wykresów podzieliłem badany okres na sezony, w celu przeprowadzenia analizy sezonowości. Najpierw jednak policzyłem podstawowe miary statystyczne dla całego okresu:

Średnią arytmetyczną liczę ze wzoru:

. (1.1)

Dla BZT5 wynosi ona 324,7[mg/dm³], a dla CHZT 886,3[mg/dm³].

Kwantyle (i medianę) odczytuję z wykresów skumulowanych częstości względnych. Wykresy te (rys.1.5 i rys.1.6) załączone są na końcu tej części projektu.

Empiryczny obszar zmienności, będący różnicą między największą i najmniejszą wartością zmiennej w badanej zbiorowości, obliczam tylko dla wstępnej orientacji, na jakim obszarze rozciągają się wartości badanej zmiennej.

Wynosi on R_BZT = 647,5[mg/dm³], a R_CHZT = 1443,8[mg/dm³].

Wariancja pozwala na określenie zróżnicowania zbiorowości, im wyższa jest jej wartość, tym bardziej zbiorowość jest zróżnicowana. Do wyznaczenia tej wartości stosuję wzór:

. (1.3)

s²_BZT = 14042,1[(mg/dm³)²]; s²_CHZT = 71241,1[(mg/dm³)²].

Odchylenie standardowe określa, o ile wszystkie jednostki danej zbiorowości różnią się średnio od średniej arytmetycznej badanej zbiorowości. Korzystam tu ze wzoru:

. (1.4)

Dla BZT₅ wynosi ono 118,5[mg/dm³], a dla CHZT 266,9[mg/dm³]

Współczynniki zmienności informują o sile dyspersji. Duże ich wartości świadczą o niejednorodności zbiorowości. Za ich pomocą można porównywać cechy tej samej zbiorowości będące na różnym poziomie. Korzystam tu ze wzoru:

. (1.5)

BZT₅: V_s = 36,5[%]; CHZT: V_s = 82,2[%] .

W przypadku BZT₅ na podstawie graficznych wykresów nie ma powodu, który wskazywałby na podział na sezony w jakiś konkretny sposób. Dlatego do analizy sezonowości podzieliłem rok na dwie połowy (po 6 miesięcy).

Dla CHZT rok dzielę na początku VI miesiąca. Przed tą datą brak znacznych przyrostów czy spadków, po niej natomiast obserwuje bardzo duży rozrzut pomiarów.

Zgodnie z poleceniem zadania, analiza statystyczna badanego zjawiska zawiera wyniki:

1. analizy zmienności sezonowych na podstawie wartości średnich i wariancji;

2. przedziały ufności dla wartości średnich;

3. analizę trendu.

Ad. A

Do zbadania istotności różnicy dwóch średnich przez weryfikację H₀:
=
zastosowałem statystykę:

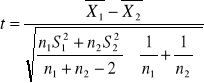
. (1.6)

Dla BZT₅:

.

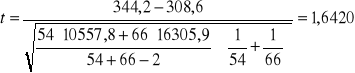
Dla CHZT:

.

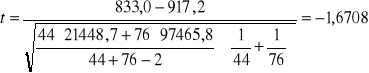
Wartość t_ odczytana z tablic rozkładu t-Studenta (=0,01, ss=n₁+n₂-2=118) wynosi, dla obu wskaźników, około 2,617.

Ponieważ |t_|>|t| nie ma podstaw do odrzucenia H₀. Oznacza to, że w obu przypadkach brak jest istotnej różnicy w wielkościach średnich.

Zweryfikowałem następnie hipotezę o jednakowym stopniu rozproszenia wartości badanej cechy. Do tego celu zakładam jednorodność wariancji w porównywanych populacjach.

H₀:
; H₁:
; test istotności służący do weryfikacji hipotezy zerowej:

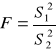
. (1.8)

Statystyka ta ma rozkład F Snedecora z n₁-1 oraz n₂-1 stopniami swobody, pamiętając, że koniecznym jest aby
. Współczynnik  przyjąłem 0,01.

Dla BZT₅:

.

Dla CHZT:

.

Z tablic rozkładu F Snedecora odczytałem wartość F_=1,89. Z uwagi na to, że wartości krytyczne w tablicy są podane dla stopni swobody 40-60 i 60-60 wartość F_ jest tylko przybliżona. O tym, że nie spowoduje to błędnej weryfikacji hipotezy zerowej świadczy fakt, że w stosunku do BZT₅ wartość krytyczna, przy niewielkich zmianach wartości, będzie na pewno większa, a dla CHZT mniejsza.

W przypadku BZT₅ niema podstaw do odrzucenia H₀ , co oznacza, że wariancje na poziomie istotności  są sobie równe.

Dla CHZT odrzucam hipotezę zerową o równości rozproszenia badanej cechy.

Ad. B

Przedziały ufności wyznaczyłem ze wzoru:

; (1.7)

t_ odczytałem z tablicy rozkładu t-Studenta dla n-1 liczby stopni swobody.

Tablica 1.1. dane do obliczeń.

	BZT5		CHZT
	sezon I	sezon II	sezon I	sezon II
Σ	18588,8	20369,6	36651,5	69710,0
n	54	66	44	76
	344,2	308,6	833,0	917,2
s^2	10577,8	16305,9	21448,7	97465,8
t	2,010	1,999	2,020	1,997
przedziały ufności:
lewy	315,8	276,9	787,9	845,2
prawy	372,6	340,3	878,1	989,2

Ad. C

Test Spearmana.

H₀: R_sp=0 brak trendu;

H₁: R_sp≤0 \

≥0 /^{linia trendu;}

Skorzystałem ze statystyki:

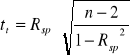
, (1.9)

gdzie:

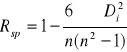
, (1.10)

. (1.11)

Krytyczne wartości t odczytane są z rozkładu t-Studenta dla n-2 stopni swobody:

t_118,0.025 = 1,980

t_118,0.975 =-1,980.

Tablica 1.2. Wyniki obliczeń.

	BZT5	CHZT
Rsp	-0,0623	0,2091
t	-0,6586	2,5538

W przypadku BZT₅ obliczona wartość t zawiera się w przedziale (t_n-2,0.025;t_n-2,0.975) co oznacza, że nie ma podstaw do odrzucenia hipotezy zerowej - brak jest linii trendu.

Test Spearmana pozwala stwierdzić na podstawie wyniku t>t_kr, że dla rozkładu CHZT w ściekach, występuje trend wzrostowy, przy współczynniku R_sp=0,21.

Interpretacja wyników:

Na podstawie histogramów (rys.1.1 i rys.1.2), jak i wartości średniej arytmetycznej, widać, że ładunek w dopływających ściekach CHZT jest ponad dwukrotnie większy niż w przypadku BZT₅.

Zbiorowość jest mało zróżnicowana, ładunki BZT₅ i CHZT, na przestrzeni roku, były bliskie średniej całorocznej. Świadczą o tym wartości odchyleń przeciętnych i wariancji, są one bardzo małe i dodatkowo są one na podobnym poziomie.

Potwierdzeniem nieznacznej tylko zmienności wielkości ładunków jest wartość odchylenia standardowego, które wynosi średnio dla BZT₅ i CHZT tylko 0,5[mg/dm³] - jest to wartość bardzo mała w odniesieniu do wielkości poszczególnych ładunków tych wskaźników występujących w ściekach.

Obliczone współczynniki zmienności są bardzo małe, co świadczy zarówno o jednorodności badanej zbiorowości, jak i zebranych danych.

Z analizy sezonowości:

Przy dokonanym przeze mnie podziale na dwa sezony, dla każdego ze wskaźników, średnie wartości ładunków nie różnią się od siebie w istotny sposób. Brak więc jest sezonowości zjawisk ze względu na zmiany wartości oczekiwanych o obu sezonach.

Trochę inaczej wygląda to w przypadku sezonowości ze względu na wariancję w poszczególnych sezonach.

W przypadku BZT₅, na poziomie =0.01, przyjmuję hipotezę o jednakowym stopniu rozproszenia wartości ładunku - brak więc znów sezonowości.

Dla CHZT jednak zaznacza się istotność w nierówności rozproszenia, ma więc miejsce zjawisko sezonowości.

Potwierdzeniem braku sezonowości dla BZT₅, a sezonowości wielkości CHZT, jest analiza trendu testem Spearmana.

Obliczenia do tej analizy wykonałem bez podziału na sezony, co miało na celu sprawdzenie występowania zjawiska trendu w całym roku. Znalazłem w ten sposób potwierdzenie wyników analizy sezonowości: brak linii trendu dla BZT₅ i trend wzrostowy w przypadku CHZT. Oznacza to zupełny brak sezonowości wielkości występowania BZT₅, a sezonowość CHZT - dokładnie wzrost wielkości ładunku w II sezonie.

---