Uniwersytet Warmińsko-Mazurski w Olsztynie Olsztyn,08.03.2006r.
Wydział Geodezji i Gospodarki Przestrzennej
Kierunek : Geodezja i Kartografia
Specjalność: Geodezja i SIP
Wyrównanie sieci geodezyjnej na elipsoidzie
Wyrównanie sieci: metoda obliczenia wyrównanych współrzędnych punktów 2, 3, 4 w sieci.
Wykonanie zadań odwrotnych dla 6 linii metodą Gaussa.
Ułożenie układu równań poprawek V=AX+L
Eliminacja stałej orientacji.
Eliminacja niewiadomej z równania warunkowego.
Ułożenie układu równań normalnych (ATPA)X+ATPL=0
Rozwiązanie układu równań normalnych.
Obliczenie wyrównanych współrzędnych i ich błędów.
Kontrola obliczeń.
Dane:
S1-2 = 23724,552 m
B1= 53 o 39 ` 23 ”,2647
L1= 20 o 40 '58 ”,0527
A1-2 = 0o09'08”,59
Błędy pomiarowe:
mS 1-2 = 0,057 m
mk = 0,7”
Kierunki:
Bok |
Kierunek o ` ” |
1-2 |
00 00 00,0 |
1-3 |
36 18 40,43 |
1-4 |
89 15 11,94 |
2-3 |
00 00 00,0 |
2-4 |
52 47 42,79 |
2-1 |
88 02 58,81 |
3-4 |
00 00 00,0 |
3-1 |
35 19 51,31 |
3-2 |
90 58 13,10 |
4-1 |
00 00 00,0 |
4-2 |
55 29 32,34 |
4-3 |
91 43 37,03 |
Przybliżone współrzędne punktów 2, 3, 4, oraz współrzędne stałe punktu 1
Nr punktu |
B O ` ” |
L O ` ” |
1 |
53 39 23,2647 |
20 40 58,0527 |
2 |
53 52 10,6159 |
20 41 01,5059 |
3 |
53 51 49,4094 |
20 56 32,1229 |
4 |
53 39 27,8873 |
20 56 02,8791 |
Rozwiązanie:
1. Wykonanie zadań odwrotnych dla 6 linii metodą Gaussa.
Dane: B1, B2, L1, L2
ΔB” = B2 - B1
ΔL” = L2 - L1
B = 0,5 * (B1 + B2)
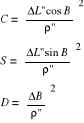


Metoda Gaussa dla linii 1 - 2 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [º] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B1 |
53 |
39 |
23,2647 |
53,65646242 |
0,936481934 |
|
|
L1 |
20 |
40 |
58,0527 |
20,68279242 |
0,360982826 |
|
|
B2 |
53 |
52 |
10,6159 |
53,86961553 |
0,940202158 |
|
|
L2 |
20 |
41 |
1,5059 |
20,68375164 |
0,360999568 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
0 |
12 |
47,3512 |
0,213153111 |
0,003720224 |
767,3512 |
|
ΔL = |
0 |
0 |
3,4532 |
0,000959222 |
1,67416E-05 |
3,4532 |
|
B = |
53 |
45 |
46,9403 |
53,76303897 |
0,938342046 |
|
|
|
|
|
|
|
|
|
|
C = |
9,79385E-11 |
|
M = |
6377161,735 |
Q = |
0,002354643 |
|
S = |
1,82342E-10 |
|
N = |
6392177,677 |
V2 = |
1,000005544 |
|
D = |
1,38401E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032344296 |
|
|
|
|
|
|
(2)B = |
0,032268316 |
|
u = |
23724,468 |
|
|
|
(3)B = |
0,316059157 |
|
v = |
63,260 |
|
|
|
(4)B = |
5,97241E-07 |
|
ΔA = |
2,7853 |
1,35034E-05 |
|
|
(5)B = |
0,041662565 |
|
s1 - 2 = |
23724,552 |
|
|
|
(6)B = |
0,083333795 |
|
A = |
0,15277453 |
0,002666419 |
|
|
(7)B = |
0,125000462 |
|
A1 - 2 = |
0,002659667 |
|
|
|
|
|
|
A2 - 1 = |
3,144265824 |
|
|
|
|
|
|
|
|
|
|
|
A1 - 2 = |
0º |
9' |
8",60 |
0,152387685 |
0,002659667 |
|
|
A2 - 1 = |
180º |
9' |
11",38 |
180,1531614 |
3,144265824 |
|
|
s1 - 2 = |
23724,552 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Metoda Gaussa dla linii 1 - 3 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [ş] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B1 |
53 |
39 |
23,2647 |
53,65646242 |
0,936481934 |
|
|
L1 |
20 |
40 |
58,0527 |
20,68279242 |
0,360982826 |
|
|
B3 |
53 |
51 |
49,4094 |
53,86372483 |
0,940099346 |
|
|
L3 |
20 |
56 |
32,1229 |
20,94225636 |
0,365511326 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
0 |
12 |
26,1447 |
0,207262417 |
0,003617412 |
746,1447 |
|
ΔL = |
0 |
15 |
34,0702 |
0,259463944 |
0,0045285 |
934,0702 |
|
B = |
53 |
45 |
36,3371 |
53,76009363 |
0,93829064 |
|
|
|
|
|
|
|
|
|
|
C = |
7,16688E-06 |
|
M = |
6377158,583 |
Q = |
0,002355 |
|
S = |
1,33404E-05 |
|
N = |
6392176,624 |
V2 = |
1,0000055 |
|
D = |
1,30857E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032344312 |
|
|
|
|
|
|
(2)B = |
0,032268321 |
|
u = |
23068,755 |
|
|
|
(3)B = |
0,316008979 |
|
v = |
17112,511 |
|
|
|
(4)B = |
5,9713E-07 |
|
ΔA = |
753,3748 |
0,003652464 |
|
|
(5)B = |
0,041662564 |
|
s1 - 3 = |
28722,909 |
|
|
|
(6)B = |
0,083333795 |
|
A = |
36,56819823 |
0,638235461 |
|
|
(7)B = |
0,125000462 |
|
A1 - 3 = |
0,636409229 |
|
|
|
|
|
|
A3 - 1 = |
3,781654346 |
|
|
|
|
|
|
|
|
|
|
|
A1 - 3 = |
36º |
27' |
48",83 |
36,46356284 |
0,636409229 |
|
|
A3 - 1 = |
216º |
40' |
22",20 |
216,6728336 |
3,781654346 |
|
|
s1 - 3 = |
28722,909 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Metoda Gaussa dla linii 1 - 4 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [º] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B1 |
53 |
39 |
23,2647 |
53,65646242 |
0,936481934 |
|
|
L1 |
20 |
40 |
58,0527 |
20,68279242 |
0,360982826 |
|
|
B4 |
53 |
39 |
27,8873 |
53,65774647 |
0,936504345 |
|
|
L4 |
20 |
56 |
2,8791 |
20,93413308 |
0,365369548 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
0 |
0 |
4,6226 |
0,001284056 |
2,2411E-05 |
4,6226 |
|
ΔL = |
0 |
15 |
4,8264 |
0,251340667 |
0,004386722 |
904,8264 |
|
B = |
53 |
39 |
25,576 |
53,65710444 |
0,93649314 |
|
|
|
|
|
|
|
|
|
|
C = |
6,75815E-06 |
|
M = |
6377048,291 |
Q = |
0,0023665 |
|
S = |
1,24852E-05 |
|
N = |
6392139,773 |
V2 = |
1,0000056 |
|
D = |
5,02253E-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032344871 |
|
|
|
|
|
|
(2)B = |
0,032268507 |
|
u = |
142,916 |
|
|
|
(3)B = |
0,314262249 |
|
v = |
16617,276 |
|
|
|
(4)B = |
5,93223E-07 |
|
ΔA = |
728,8244 |
0,00353344 |
|
|
(5)B = |
0,041662553 |
|
s1 - 4 = |
16617,890 |
|
|
|
(6)B = |
0,0833338 |
|
A = |
89,50724383 |
1,562196109 |
|
|
(7)B = |
0,125000467 |
|
A1 - 4 = |
1,560429389 |
|
|
|
|
|
|
A4 - 1 = |
4,705555483 |
|
|
|
|
|
|
|
|
|
|
|
A1 - 4 = |
89º |
24' |
21",66 |
89,40601823 |
1,560429389 |
|
|
A4 - 1 = |
269º |
36' |
30",49 |
269,6084694 |
4,705555483 |
|
|
s1 - 4 = |
16617,890 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Metoda Gaussa dla linii 2 - 3 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [ş] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B2 |
53 |
52 |
10,6159 |
53,86961553 |
0,940202158 |
|
|
L2 |
20 |
41 |
1,5059 |
20,68375164 |
0,360999568 |
|
|
B3 |
53 |
51 |
49,4094 |
53,86372483 |
0,940099346 |
|
|
L3 |
20 |
56 |
32,1229 |
20,94225636 |
0,365511326 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
(-)0 |
0 |
21,2065 |
-0,005890694 |
-0,000102812 |
-21,2065 |
|
ΔL = |
0 |
15 |
30,617 |
0,258504722 |
0,004511759 |
930,6170 |
|
B = |
53 |
52 |
0,0126 |
53,86667018 |
0,940150752 |
|
|
|
|
|
|
|
|
|
|
C = |
7,0779E-06 |
|
M = |
6377272,587 |
Q = |
0,002343028 |
|
S = |
1,32781E-05 |
|
N = |
6392214,715 |
V2 = |
1,00000549 |
|
D = |
1,05703E-08 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032343734 |
|
|
|
|
|
|
(2)B = |
0,032268129 |
|
u = |
-655,659 |
|
|
|
(3)B = |
0,317832578 |
|
v = |
17006,042 |
|
|
|
(4)B = |
6,01099E-07 |
|
ΔA = |
751,6105 |
0,00364391 |
|
|
(5)B = |
0,041662576 |
|
s2 - 3 = |
17018,677 |
|
|
|
(6)B = |
0,083333791 |
|
A = |
92,20791423 |
1,6093317 |
|
|
(7)B = |
0,125000457 |
|
A2 - 3= |
1,607509745 |
|
|
|
|
|
|
A3 - 2 = |
4,752746309 |
|
|
|
|
|
|
|
|
|
|
|
A2 - 3 = |
92º |
06' |
12",69 |
92,10352389 |
1,607509745 |
|
|
A3 - 2 = |
272º |
18' |
44",30 |
272,3123046 |
4,752746309 |
|
|
s2 - 3 = |
17018,677 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Metoda Gaussa dla linii 2 - 4 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [º] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B2 |
53 |
52 |
10,6159 |
53,86961553 |
0,940202158 |
|
|
L2 |
20 |
41 |
1,5059 |
20,68375164 |
0,360999568 |
|
|
B4 |
53 |
39 |
27,8873 |
53,65774647 |
0,936504345 |
|
|
L4 |
20 |
56 |
2,8791 |
20,93413308 |
0,365369548 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
(-)0 |
12 |
42,7286 |
-0,211869056 |
-0,003697813 |
-762,7286 |
|
ΔL = |
0 |
15 |
1,3732 |
0,250381444 |
0,004369981 |
901,3732 |
|
B = |
53 |
45 |
49,2516 |
53,763681 |
0,938353251 |
|
|
|
|
|
|
|
|
|
|
C = |
6,67277E-06 |
|
M = |
6377162,422 |
Q = |
0,0023546 |
|
S = |
1,2424E-05 |
|
N = |
6392177,907 |
V2 = |
1,0000055 |
|
D = |
1,36738E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032344292 |
|
|
|
|
|
|
(2)B = |
0,032268314 |
|
u = |
-23581,502 |
|
|
|
(3)B = |
0,316070096 |
|
v = |
16512,084 |
|
|
|
(4)B = |
5,97265E-07 |
|
ΔA = |
727,0364 |
0,003524772 |
|
|
(5)B = |
0,041662565 |
|
s2 - 4 = |
28787,778 |
|
|
|
(6)B = |
0,083333795 |
|
A = |
144,9997742 |
2,530723474 |
|
|
(7)B = |
0,125000462 |
|
A2 - 4 = |
2,528961088 |
|
|
|
|
|
|
A4 - 2 = |
5,674078514 |
|
|
|
|
|
|
|
|
|
|
|
A2 - 4 = |
144º |
53' |
55",69 |
144,8987969 |
2,528961088 |
|
|
A4 - 2 = |
325º |
06' |
02",70 |
325,1007515 |
5,674078514 |
|
|
s2 - 4 = |
28787,778 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Metoda Gaussa dla linii 3 - 4 |
|||||||
Elipsoida Krasowskiego: |
|
|
|
|
|
|
|
a = |
6378245 |
|
ρ" = |
206264,8062 |
|
|
|
e2 = |
0,006693421623 |
|
ρº = |
57,29577951 |
|
|
|
(e')2 = |
0,006738525415 |
|
|
|
|
|
|
DANE |
|
|
|||||
|
stopnie [ş] |
minuty ['] |
sekundy ["] |
liczba |
radiany |
|
|
B3 |
53 |
51 |
49,4094 |
53,86372483 |
0,940099346 |
|
|
L3 |
20 |
56 |
32,1229 |
20,94225636 |
0,365511326 |
|
|
B4 |
53 |
39 |
27,8873 |
53,65774647 |
0,936504345 |
|
|
L4 |
20 |
56 |
2,8791 |
20,93413308 |
0,365369548 |
|
|
|
|
|
|
|
|
sekundy ["] |
|
ΔB = |
(-)0 |
12 |
21,5221 |
-0,205978361 |
-0,003595001 |
-741,5221 |
|
ΔL = |
(-)0 |
0 |
29,2438 |
-0,008123278 |
-0,000141778 |
-29,2438 |
|
B = |
53 |
45 |
38,6483 |
53,76073565 |
0,938301845 |
|
|
|
|
|
|
|
|
|
|
C = |
7,02466E-09 |
|
M = |
6377159,27 |
Q = |
0,0023549 |
|
S = |
1,30763E-08 |
|
N = |
6392176,853 |
V2 = |
1,0000055 |
|
D = |
1,2924E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)B = |
0,032344308 |
|
|
|
|
|
|
(2)B = |
0,03226832 |
|
u = |
-22925,891 |
|
|
|
(3)B = |
0,316019916 |
|
v = |
-535,749 |
|
|
|
(4)B = |
5,97154E-07 |
|
ΔA = |
-23,5868 |
-0,000114352 |
|
|
(5)B = |
0,041662565 |
|
s3 - 4 = |
22932,150 |
|
|
|
(6)B = |
0,083333795 |
|
A = |
181,3386869 |
3,164957148 |
|
|
(7)B = |
0,125000462 |
|
A3 - 4 = |
3,165014324 |
|
|
|
|
|
|
A4 - 3 = |
6,306492625 |
|
|
|
|
|
|
|
|
|
|
|
A3 - 4 = |
181º |
20' |
31",07 |
181,3419629 |
3,165014324 |
|
|
A4 - 3 = |
1º |
20' |
07",48 |
361,335411 |
6,306492625 |
|
|
s3 - 4 = |
22932,150 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Ułożenie układu równań poprawek V=AX+L
Po oznaczeniu ogólnych symboli współczynników stojących przy parametrach:

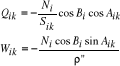
otrzymamy równania poprawek dla długości:
![]()
dla azymutu:
![]()
dla kierunku:
![]()
gdzie ![]()
; dzi - poprawka do stałej orientacji
obliczenie współczynników przy parametrach:
|
Pik |
Qik |
Uik |
Wik |
1-2 |
0,714905055 |
-159,671 |
-30,91668988 |
-0,048846 |
1-3 |
131,9487672 |
-106,067 |
-24,86437125 |
-10,91479 |
1-4 |
383,7253022 |
-2,36316 |
-0,320506787 |
-18,36446 |
2-3 |
374,4696712 |
8,12884 |
1,134846991 |
-18,26036 |
2-4 |
127,3831083 |
107,1138 |
25,29510214 |
-10,50719 |
2-1 |
-0,718560407 |
158,8648 |
30,91779478 |
0,048846 |
3-4 |
-6,51280597 |
164,3328 |
30,90939472 |
0,427997 |
3-1 |
-132,6046673 |
105,2606 |
24,79795701 |
10,91479 |
3-2 |
-374,4166962 |
-8,93649 |
-1,247424134 |
18,26036 |
4-1 |
-383,7370462 |
1,557676 |
0,211268269 |
18,36446 |
4-2 |
-126,7389829 |
-107,92 |
-25,35670836 |
10,50719 |
4-3 |
6,480790133 |
-165,139 |
-30,9084088 |
-0,427997 |
Poprawki:
VS1-2=30,918dB2+0,049dL2 -7,69929E-05
Vk1-2= -0,719dB2+158,865dL2-dz'1-1,50375E-06
Vk1-3= -132,605dB3+105,261dL3-dz'1-2,47071E-06
Vk1-4= -383,737dB4+1,558dL4-dz'1+3,97445E-06
Vk2-3=374,4165,139dL470 dB2+8,129dL2-374,417dB3-8,936dL3-dz'2-1,2585E-07
Vk2-4=127,383 dB2+107,114dL2-126,739dB4-107,920dL4-dz'2+8,09429E-07
Vk2-1= -0,719dB2+158,865dL2-dz'2 -6,8358E-07
Vk3-4= -6,513dB3+164,333dL3+6,481dB4-165,139dL4-dz'3+7,27311E-08
Vk3-1= -132,605dB3+105,261dL3-dz'3 - 7,76687E-07
Vk3-2= 374,470dB2+8,129dL2-374,417dB3-8,936dL3-dz'3 +7,03955E-07
Vk4-1=-383,737dB4+ 1,558dL4-dz'4 +2,66849E-07
Vk4-2=127,383 dB2+107,114dL2-126,739dB4-107,920dL4-dz'4-3,37366E-07
Vk4-3= -6,513dB3+164,333dL3+6,481dB4-165,139dL4-dz'4+ 7,05163E-08
4.Eliminacja stałej orientacji.
|
dB2 |
dL2 |
dB3 |
dL3 |
dB4 |
dL4 |
dz1' |
dz2' |
dz3' |
dz4' |
L |
VK1 - 2 = |
-0,719 |
158,865 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
-1,5E-06 |
VK1 - 3 = |
0 |
0 |
-132,605 |
105,261 |
0 |
0 |
-1 |
0 |
0 |
0 |
-2,5E-06 |
VK1 - 4 = |
0 |
0 |
0 |
0 |
-383,737 |
1,558 |
-1 |
0 |
0 |
0 |
4E-06 |
suma: |
-0,719 |
158,865 |
-132,605 |
105,26 |
-383,737 |
1,55768 |
-3 |
0 |
0 |
0 |
-2,5E-16 |
suma/(-3) |
0,23952014 |
-52,955 |
44,2016 |
-35,087 |
127,912 |
-0,5192 |
1 |
0 |
0 |
0 |
8,4E-17 |
|
|
|
|
|
|
|
|
|
|
|
|
vk2-3= |
374,470 |
8,129 |
-374,417 |
-8,936 |
0 |
0 |
0 |
-1 |
0 |
0 |
-1,3E-07 |
vk2-4= |
127,383 |
107,114 |
0,000 |
0 |
-126,739 |
-107,920 |
0 |
-1 |
0 |
0 |
0,000001 |
vk2-1= |
-0,719 |
158,865 |
0,000 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
-6,8E-07 |
suma: |
501,134 |
274,107 |
-374,417 |
-8,936 |
-126,739 |
-107,920 |
0 |
-3 |
0 |
0 |
0,000 |
suma/(-3) |
-167,04474 |
-91,369 |
124,806 |
2,9788 |
42,2463 |
35,9735 |
0 |
1 |
0 |
0 |
-1,1E-16 |
|
|
|
|
|
|
|
|
|
|
|
|
vk3-4= |
0 |
0 |
-6,513 |
164,333 |
6,481 |
-165,14 |
0 |
0 |
-1 |
0 |
7,3E-08 |
vk3-1= |
0 |
0 |
-132,605 |
105,261 |
0 |
0 |
0 |
0 |
-1 |
0 |
-7,8E-07 |
vk3-2= |
374,470 |
8,129 |
-374,417 |
-8,936 |
0 |
0 |
0 |
0 |
-1 |
0 |
7E-07 |
suma: |
374,470 |
8,129 |
-513,534 |
260,657 |
6,481 |
-165,139 |
0,000 |
0,000 |
-3,000 |
0,000 |
0,000 |
suma/(-3) |
-124,823224 |
-2,7096 |
171,178 |
-86,886 |
-2,16026 |
55,0464 |
0 |
0 |
1 |
0 |
7,4E-17 |
|
|
|
|
|
|
|
|
|
|
|
|
vk4-1= |
0 |
0 |
0 |
0 |
-383,737 |
1,558 |
0 |
0 |
0 |
-1 |
2,7E-07 |
vk4-2= |
127,383 |
107,114 |
0 |
0 |
-126,739 |
-107,92 |
0 |
0 |
0 |
-1 |
-3,4E-07 |
vk4-3= |
0 |
0 |
-6,513 |
164,333 |
6,481 |
-165,14 |
0 |
0 |
0 |
-1 |
7,1E-08 |
suma: |
127,383 |
107,114 |
-6,513 |
164,333 |
-503,995 |
-271,502 |
0 |
0 |
0 |
-3 |
1,6E-15 |
suma/(-3) |
-42,4610361 |
-35,705 |
2,17094 |
-54,778 |
167,998 |
90,5007 |
0 |
0 |
0 |
1 |
-5,2E-16 |
Ułożenie układu V=AX+L po eliminacji dz'i
|
dB2 |
dL2 |
dB3 |
dL3 |
dB4 |
dL4 |
L" |
vs1-2= |
30,918 |
0,049 |
0 |
0 |
0 |
0 |
-7,7E-05 |
vk1-2= |
-0,479 |
105,910 |
44,2016 |
-35,087 |
127,912 |
-0,5192 |
-0,31017 |
vk1-3= |
0,240 |
-52,955 |
-88,4031 |
70,174 |
127,912 |
-0,5192 |
-0,50962 |
vk1-4= |
0,240 |
-52,955 |
44,2016 |
-35,087 |
-255,825 |
1,03845 |
0,81979 |
vk2-3= |
207,425 |
-83,240 |
-249,611 |
-5,958 |
42,246 |
35,973 |
-0,02596 |
vk2-4= |
-39,662 |
15,745 |
124,806 |
2,979 |
-84,493 |
-71,947 |
0,16696 |
vk2-1= |
-167,763 |
67,496 |
124,806 |
2,979 |
42,246 |
35,973 |
-0,141 |
vk3-4= |
-124,823 |
-2,710 |
164,665 |
77,447 |
4,321 |
-110,093 |
0,015 |
vk3-1= |
-124,823 |
-2,710 |
38,573 |
18,375 |
-2,160 |
55,046 |
-0,1602 |
vk3-2= |
249,646 |
5,419 |
-203,239 |
-95,822 |
-2,160 |
55,046 |
0,1452 |
vk4-1= |
-42,461 |
-35,705 |
2,171 |
-54,778 |
-215,739 |
92,058 |
0,05504 |
vk4-2= |
84,922 |
71,409 |
2,171 |
-54,778 |
41,259 |
-17,420 |
-0,06959 |
vk4-3= |
-42,461 |
-35,705 |
-4,342 |
109,555 |
174,479 |
-74,639 |
0,01455 |
Eliminacja niewiadomej z równania warunkowego.
.VA1-2=P21dB2+Q21dL2+L=0
dL2==(-P2,1/Q2,1)*dB2 - L/Q2-1 = 0,004523*dB2-1,7294E-10
|
dB2 |
dB3 |
dL3 |
dB4 |
dL4 |
L'' |
vs1-2= |
30,918 |
0 |
0 |
0 |
0 |
-8E-05 |
vk1-2= |
0,000 |
44,2016 |
-35,086879 |
127,912 |
-0,5192 |
-0,3102 |
vk1-3= |
0,000 |
-88,4031 |
70,1737587 |
127,912 |
-0,5192 |
-0,5096 |
vk1-4= |
0,000 |
44,2016 |
-35,086879 |
-255,82 |
1,03845 |
0,8198 |
vk2-3= |
207,048 |
-249,611 |
-5,958 |
42,246 |
35,973 |
-0,026 |
vk2-4= |
-39,590 |
124,806 |
2,979 |
-84,493 |
-71,947 |
0,167 |
vk2-1= |
-167,458 |
124,806 |
2,979 |
42,246 |
35,973 |
-0,141 |
vk3-4= |
-124,835 |
164,665 |
77,447 |
4,321 |
-110,093 |
0,015 |
vk3-1= |
-124,835 |
38,573 |
18,375 |
-2,160 |
55,046 |
-0,1602 |
vk3-2= |
249,671 |
-203,239 |
-95,822 |
-2,160 |
55,046 |
0,1452 |
vk4-1= |
-42,623 |
2,171 |
-54,778 |
-215,739 |
92,058 |
0,055 |
vk4-2= |
85,245 |
2,171 |
-54,778 |
41,259 |
-17,420 |
-0,0696 |
vk4-3= |
-42,623 |
-4,342 |
109,555 |
174,479 |
-74,639 |
0,0145 |
6. Ułożenie układu równań normalnych (ATPA)X+ATPL=0
|
ATPAX + ATPL = 0 |
|
|
X = (ATPA)-1 ATPL |
|
|
V = AX + L |
|
A= |
30,91801572 |
0 |
0 |
0 |
0 |
|
0 |
44,20155578 |
-35,08688 |
127,9123487 |
-0,519225287 |
|
0 |
-88,40311157 |
70,173759 |
127,9123487 |
-0,519225287 |
|
0 |
44,20155578 |
-35,08688 |
-255,8246975 |
1,038450573 |
|
207,0484278 |
-249,6111308 |
-5,957659 |
42,24632764 |
35,97345754 |
|
-39,5904168 |
124,8055654 |
2,9788293 |
-84,49265528 |
-71,94691509 |
|
-167,458011 |
124,8055654 |
2,9788293 |
42,24632764 |
35,97345754 |
|
-124,8354796 |
164,6652505 |
77,447146 |
4,320526755 |
-110,0928992 |
|
-124,8354796 |
38,57338916 |
18,37499 |
-2,160263378 |
55,04644962 |
|
249,6709591 |
-203,2386397 |
-95,82214 |
-2,160263378 |
55,04644962 |
|
-42,62253139 |
2,170935323 |
-54,7776 |
-215,7386332 |
92,05835774 |
|
85,24506277 |
2,170935323 |
-54,7776 |
41,25943008 |
-17,41969076 |
|
-42,62253139 |
-4,341870647 |
109,5552 |
174,4792031 |
-74,63866698 |
AT= |
30,918 |
0 |
0 |
0 |
207,05 |
-39,59 |
-167,5 |
-124,8 |
-124,8 |
249,67 |
-42,62 |
85,24506 |
-42,62253 |
|
0 |
44,202 |
-88,4 |
44,202 |
-249,6 |
124,81 |
124,81 |
164,67 |
38,573 |
-203,2 |
2,1709 |
2,170935 |
-4,341871 |
|
0 |
-35,087 |
70,174 |
-35,09 |
-5,958 |
2,9788 |
2,9788 |
77,447 |
18,375 |
-95,82 |
-54,78 |
-54,7776 |
109,5552 |
|
0 |
127,91 |
127,91 |
-255,8 |
42,246 |
-84,49 |
42,246 |
4,3205 |
-2,16 |
-2,16 |
-215,7 |
41,25943 |
174,4792 |
|
0 |
-0,5192 |
-0,519 |
1,0385 |
35,973 |
-71,95 |
35,973 |
-110,1 |
55,046 |
55,046 |
92,058 |
-17,41969 |
-74,63867 |
P= |
302,994 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,0408 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,040816 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,040816 |
ATP= |
9367,96 |
0 |
0 |
0 |
422,55 |
-80,8 |
-341,8 |
-254,8 |
-254,8 |
509,53 |
-86,98 |
173,9695 |
-86,98476 |
|
0 |
90,207 |
-180,4 |
90,207 |
-509,4 |
254,71 |
254,71 |
336,05 |
78,721 |
-414,8 |
4,4305 |
4,43048 |
-8,860961 |
|
0 |
-71,606 |
143,21 |
-71,61 |
-12,16 |
6,0792 |
6,0792 |
158,06 |
37,5 |
-195,6 |
-111,8 |
-111,791 |
223,582 |
|
0 |
261,05 |
261,05 |
-522,1 |
86,217 |
-172,4 |
86,217 |
8,8174 |
-4,409 |
-4,409 |
-440,3 |
84,20292 |
356,08 |
|
0 |
-1,0596 |
-1,06 |
2,1193 |
73,415 |
-146,8 |
73,415 |
-224,7 |
112,34 |
112,34 |
187,87 |
-35,55039 |
-152,3238 |
ATPA= |
650623 |
-312978 |
-91307 |
19356 |
46246 |
|
-312978 |
357384 |
51323 |
-67038 |
-81851 |
|
-91307 |
51323 |
83594 |
86247 |
-51901 |
|
19355,8 |
-67038 |
86247 |
382846 |
-52236 |
|
46245,8 |
-81851 |
-51901 |
-52236 |
82237 |
L= |
-8E-05 |
|
-0,31 |
|
-0,51 |
|
0,8198 |
|
-0,026 |
|
0,167 |
|
-0,141 |
|
0,015 |
|
-0,16 |
|
0,1452 |
|
0,055 |
|
-0,07 |
|
0,0145 |
ATPL= |
115,83 |
|
89,761 |
|
-136,2 |
|
-709,9 |
|
-28,62 |
(ATPA)-1= |
3,45258E-06 |
3,3526E-06 |
4,224E-06 |
1,65264E-08 |
4,07132E-06 |
|
3,3526E-06 |
7,6419E-06 |
2,273E-06 |
1,78773E-06 |
8,29091E-06 |
|
4,22352E-06 |
2,2733E-06 |
2,934E-05 |
-4,285E-06 |
1,56805E-05 |
|
1,65264E-08 |
1,7877E-06 |
-4,285E-06 |
4,11905E-06 |
1,68215E-06 |
|
4,07132E-06 |
8,2909E-06 |
1,568E-05 |
1,68215E-06 |
2,90872E-05 |
X= |
0,0000 |
dB2 |
|
0,0007 |
dB3 |
|
0,0007 |
dL3 |
|
0,0022 |
dB4 |
|
0,0029 |
dL4 |
8. Obliczenie wyrównanych współrzędnych .
![]()
|
o ` ” |
|
o ` ” |
B1wyr |
53 39 23,2647 |
L1wyr |
20 40 58,0527 |
B2wyr |
53 52 10,6159 |
L2wyr |
20 41 01,5059 |
B3wyr |
53 51 49,4101 |
L3wyr |
20 56 32,1236 |
B4wyr |
53 39 27,8895 |
L4wyr |
20 56 02,8820 |
Do wyznaczenia błędów współrzędnych wyrównanych najpierw obliczamy macierz V ze wzoru V=AX+L, otrzymamy:
V= |
7,98392E-12 |
|
-0,0189618 |
|
-0,24223944 |
|
0,261201241 |
|
-0,01475888 |
|
-0,13853803 |
|
0,153296909 |
|
-0,12305229 |
|
0,038458065 |
|
0,084594226 |
|
-0,19137873 |
|
-0,06600001 |
|
0,257378737 |
Obliczamy mo:
![]()
gdzie m: ilość obserwacji i n: ilość niewiadomych
m0= |
0,277184663 |
Błędy wyrównanych współrzędnych obliczamy ze wzoru:
![]()
mB2 = |
0,0005 |
mB3 = |
0,0008 |
mL3 = |
0,0015 |
mB4 = |
0,0006 |
mL4 = |
0,0015 |
mL2 = |
0,0000 |
mL2 = P21/Q21*mB2
9. Kontrola obliczeń.
Obliczenie wyrównanych obserwacji:
Obserwacje wyrównane |
|
||||
|
|
liczba |
[ º ] |
[ ' ] |
[ " ] |
S1-2 |
23724,552 |
|
|
|
|
K1-2 |
6,283185215250180 |
359,9999947 |
359 |
59 |
59,98103 |
K1-3 |
0,633749354235270 |
36,31116327 |
36 |
18 |
40,18776 |
K1-4 |
1,557765510497820 |
89,25338922 |
89 |
15 |
12,2012 |
K2-3 |
6,283185235626520 |
359,9999959 |
359 |
59 |
59,98524 |
K2-4 |
0,921449736967169 |
52,79518096 |
52 |
47 |
42,65146 |
K2-1 |
1,536757380302590 |
88,04971203 |
88 |
2 |
58,96329 |
K3-4 |
6,283184710605250 |
359,9999658 |
359 |
59 |
59,87694 |
K3-1 |
0,616641058512401 |
35,33093013 |
35 |
19 |
51,34845 |
K3-2 |
1,587731763614110 |
90,97032905 |
90 |
58 |
13,18459 |
K4-1 |
6,283184379349320 |
359,9999468 |
359 |
59 |
59,80862 |
K4-2 |
0,968523315415595 |
55,49229833 |
55 |
29 |
32,27399 |
K4-3 |
1,600938586600910 |
91,72702427 |
91 |
43 |
37,28737 |
Kontrola kierunków polega na utworzeniu czterech trójkątów pomiędzy punktami kolejno: trójkąt 124 , 234 , 123 , 134. Suma kątów w każdym trójkącie jest równa 180o+eksces.Kąty otrzymujemy z różnicy kierunków, ich sumę w trójkącie sprawdzamy obliczając niezależnie eksces.
Obliczenie kątów z kierunków |
|
||||
|
|
liczba |
|
|
|
α = |
0,633749446164678 |
36,31116853 |
36 |
18 |
40,20672 |
β = |
0,615307643335421 |
35,25453107 |
35 |
15 |
16,31183 |
γ = |
0,921449808520240 |
52,79518506 |
52 |
47 |
42,66622 |
δ = |
0,971090705101713 |
55,63939893 |
55 |
38 |
21,83613 |
ζ = |
0,616641655086740 |
35,33096431 |
35 |
19 |
51,47151 |
ξ = |
0,632415271185315 |
36,23472594 |
36 |
14 |
5,01337 |
η = |
0,968524243245860 |
55,49235149 |
55 |
29 |
32,46537 |
ε = |
0,924016156262545 |
52,94222596 |
52 |
56 |
32,01344 |
trójkąt |
suma kątów |
eksces |
|
|
|
123 |
180,0002836 |
1,0209 |
180 |
0 |
1,02091 |
134 |
180,0002677 |
0,9637 |
180 |
0 |
0,9637 |
124 |
180,000277 |
0,9974 |
180 |
0 |
0,99737 |
234 |
180,0002742 |
0,9872 |
180 |
0 |
0,98724 |
Obliczamy azymuty z wyrównanych współrzędnych metodą Gauss'a:
A1 - 2 = |
0 |
9 |
8,59566 |
0,152387685 |
0,0026597 |
A2 - 1 = |
180 |
9 |
11,38095 |
180,1531614 |
3,1442658 |
A1 - 3 = |
36 |
27 |
48,80238 |
36,46355622 |
0,6364091 |
A3 - 1 = |
216 |
40 |
22,1778 |
216,6728272 |
3,7816542 |
A1 - 4 = |
89 |
24 |
20,81583 |
89,40578218 |
1,5604253 |
A4 - 1 = |
269 |
36 |
29,64256 |
269,608234 |
4,7055514 |
A2 - 3 = |
92 |
6 |
12,40289 |
92,10344525 |
1,6075084 |
A3 - 2 = |
272 |
18 |
44,01394 |
272,3122261 |
4,7527449 |
A2 - 4 = |
144 |
53 |
55,06911 |
144,8986303 |
2,5289582 |
A4 - 2 = |
325 |
6 |
2,10793 |
325,1005855 |
5,6740756 |
A3 - 4 = |
181 |
20 |
30,70629 |
181,3418629 |
3,1650126 |
A4 - 3 = |
361 |
20 |
7,12131 |
361,3353115 |
6,3064909 |
Obliczamy sumy kątów w trójkątach i porównujemy eksces:
trójkąt |
suma kątów |
eksces |
|
|
|
123 |
180,0002836 |
1,0209 |
180 |
0 |
1,02091 |
134 |
180,0002677 |
0,9637 |
180 |
0 |
0,9637 |
124 |
180,0002770 |
0,9974 |
180 |
0 |
0,99737 |
234 |
180,0002742 |
0,9872 |
180 |
0 |
0,98724 |
14
Wyszukiwarka