1.wyprowadzić wzory pozwalające obliczyć elementy geometryczne potrzebne do wpisania klotoidy pomiędzy prostą a łuk
2. przygotować  dane do tyczenia punktów głównych łuku kołowego o R=500m i alfa=60stopni
3. wytyczyć punkt środkowy met biegunową i ortogonalną
4.przedstwić zasady uwzględniania łuków niwelet przy pomocy łuków parabolicznych
5. przedstawić zasadę wyznaczania pion przemieszc reperów założonych na fundamentach budynku mieszalnego wraz z algorytmem 
6. prace geodezyjne wykonywane podczas budowy fundamentów budynku wielokondygnacyjnego
7.procedura postępowania przy tyczeniu punktów w przestrzeni metodą swobodnego stanowiska
8. sposoby realizacji projektowanych wysokości pkt niwelacją tech
9. Opisać postęp przy projektowaniu i tyczeniu łuków koszowych

10.procedura tworzenia macierzy cov współrzędnych punktu tyczonego metodą swobodnego stanowiska z uwzględnieniem błędów osnowy realizacyjnej
11.zakładan i wyrównywanie przestrzennych osnów realizacyjnych
12.ustalić dokładność tyczenia punktu metodą biegunową z założeniem bezbłędności punktów osnowy realizacyjnej(wyrównanie obserwacji zależnych)
13. obliczyć błąd średni wytyczenia punktu 1 metodą biegunową  z wykorzystaniem danych przedstawionych na rysunku

14.scharakteryzować dokumenty z jakimi geodeta ma do czynienia w procesie tyczenia obiektów bud
15.scharakteryzować etapy geodezyjnego opracowania planu zagospodarowania terenu sporządzonego na mapie skali 1: 1000
16.jak ustala się dokładność tyczenia jeśli znane jest dopuszczalne odchylenie budynku d L
17. jakie obliczenia należy przeprowadzić aby przygotować dane to  tycze łuku koszowego składającego się z dwóch łuków kołowych 
18.na czym polega geodezyjne opracowanie projektu zagospodarowania terenu lub działki
19. przedstawić procedurę tyczenia punktów głównych i pośrednich pionowego łuku kołowego

20. Opisać postępowanie przy projektowaniu i tycz łuków odwrotn

21. scharakteryzowac tresc planu zagosp terenu sprzadzonego przez projektanta i przedstawić dane do tyczenia obiektów w oparciu o osnowę geodezyjną 
22. biegunowa metoda tyczenia punktów pośrednich klotoidy 
23. przedstawic sposoby tyczenia punktów posrednich płaskiego łuku kolowego met. biegunowa 
24.Przygotowanie danych do tyczenia punktów głównych łuku kołowego płaskiego
26. Przedstawić czynności geodezyjne przy formowaniu nasypów i wykopów drogowych

1.Wyprowadzić wzory pozwalające obliczyć elementy geom. Potrzebne do wpisania klotoidy pomiędzy prostą a łuk:

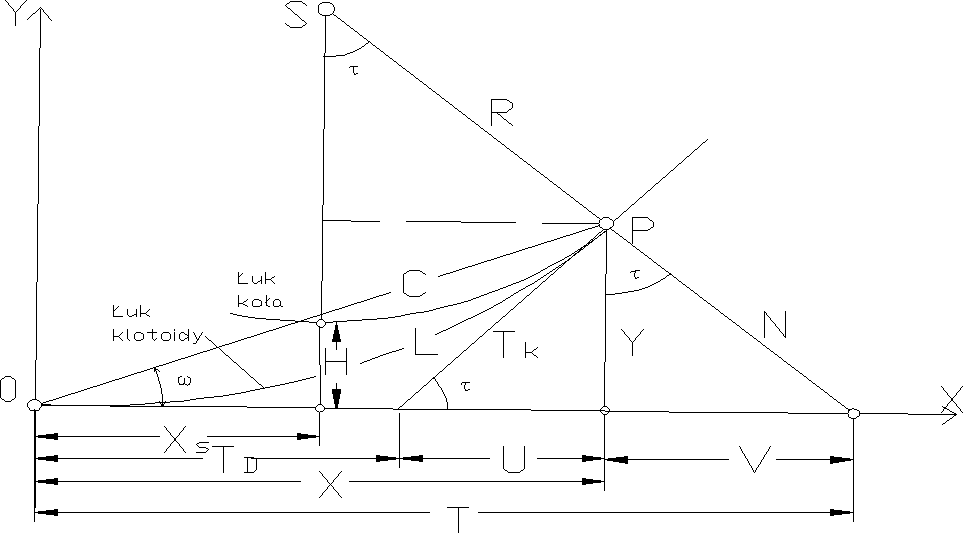
LR=a²R=a²/L ; a²dτ=L*dL ( po scałkowaniu) a²τ=L²/2+C

Stałą C wyznaczamy dla pkt początkowego klotoidy L=0 i τ=0 wtedy τ=L²/2a² lub τ=L/2R. Współrzędne dowolnego punktu na klotoidzie: dXi=dL*cosτ dXi=cos(L²/2a²)dL

dYi=dL*sinτdYi=sin(L²/2a²)dl. Występujące w równaniach funkcje sin i cos rozwijamy w szereg a następnie całkujemy aby otrzymać wzory z których wyliczymy wsp. pkt P w układzie o początku w pkt przegięcia klotoidy (L=0), w którym τ=0 dla promienia łuku R : X=L-L⁵/2a⁴+L⁹/3456a⁸+… Y=L³/6a²-L⁷/336a⁶+L¹¹/42240a¹⁰+… Pozostałe wielkości z wzorów: odcięta Xs środka koła: Xs=X-R*sinτ ; odsunięcie H łuku kołowego od stycznej głównej: H=Y-R(1-cosτ); rzędna Ys środka koła: Ys=R+H; styczna główna: T_o=X+Y*tgτ; styczna długa: T_D=X-Y*ctgτ; styczna krótka: T_K=Y/sinτ; normalna: N=Y/cosτ; podstyczna: U=Y*ctgτ; podnormalna: V=Y*tgτ; współrzędne biegunowe dowolnego punktu klotoidy: ω=arctgY/X C=pier(X²+Y²)

2.Przygotować dane do tyczenia punktów łuku kołowego o 

R=500m i α=60^o

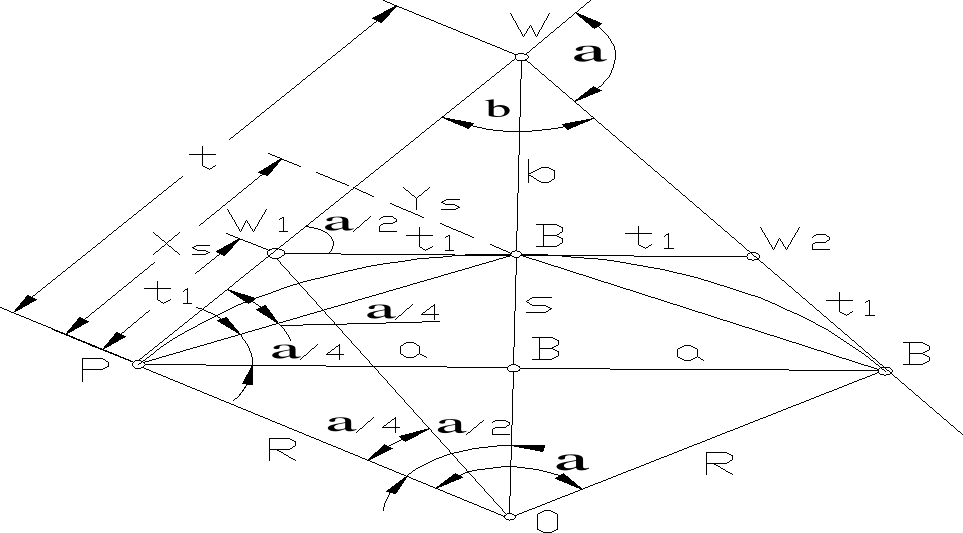
Długość stycznej głównej: t=Rtg(α/2)=, długość stycznej pomocniczej: ti=Rtg(α/4)= , odległość wierzchołkowa WS=b=(1/cos(α/2)-1)*R , połowa cięciwy PK a=R*sinα/2, długość strzałki S=R(1-cosα/2), długość łuku kołowego L=R*α/ρ (ρ^o=57,2958), długość cięciwy dla połowy łuku PS=2Rsinα/4; Odcięta pkt środkowego S Xs=PS*cosα/4=Rsin²α/4=a; rzędna pkt środkowego S Ys=PS*sinα/4=2Rsin²α/4

3.Wytyczyć punkt środkowy met biegunową i ortogonalną:

1.met biegunowa z punktu W a) na dwusiecznej kąta β=180^o-α

należy odłożyć długość WS=b: b=R/cos(α/2)-R, cosα/2=R/R+b ; b+R=R/cos(α/2) b) z punktu P lub K należy odłożyć kąt α/4 od stycznej głównej PW (KW) oraz długość |PS| PS=2Rsinα/4. 2.m ortogonalna a)na stycznej głównej PW odkładamy odciętą Xs a następnie pod kątem prostym rzędną Ys Xs=a=Rsinα/2; Ys=s=R(1-cosα/2)=2Rsin²α/4 b)od cięciwy PK odkładamy odciętą a, a następnie rzędną s.

4.Przedstwić zasady uwzględniania łuków niwelet przy pomocy

 łuków parabolicznych:

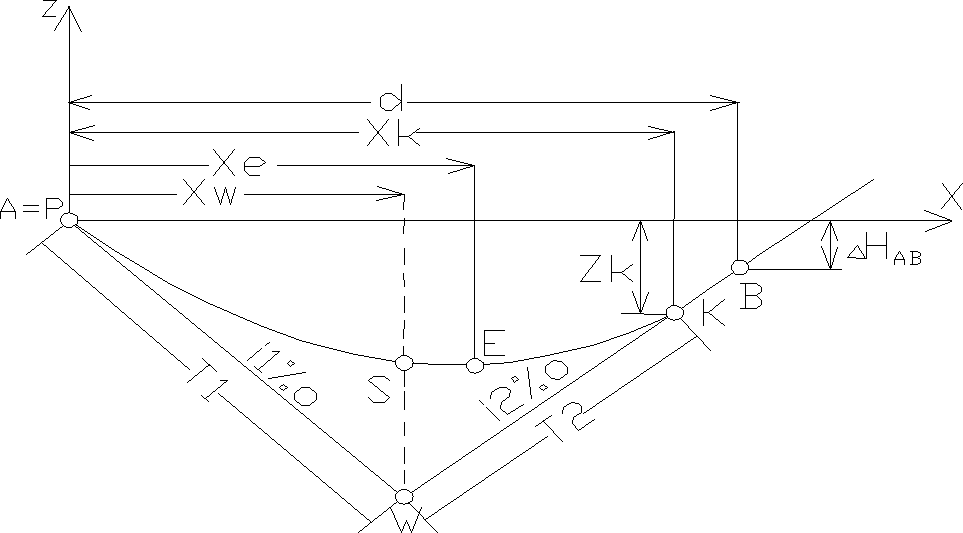
Załomy niwelety mogą być wyokrąglone łukami pionowymi w kształcie paraboli 2 stopnia. Przygotowanie danych do zaprojektowania i wytyczenia odpowiedniej paraboli prowadzi się w oparciu o ogólnie kownianie paraboli:z=ax²+bc+c przy znajomości pochylen i₁,i₂, dwoch sąsiednich odcinkow niwelety oraz różnicy wysokości H_AB i odległości d pomiędzy

dwoma punktami niwelety A i B.Równania stycznych do paraboli w punktach P i K:z^'(x_p)=2ax_p+b; z^'(x_k)=2ax_k+b;

przy czym z^'(x_p)=i₁ ; z^'(x_k)=i₂ zatem i₁=2ax_p+b i₂=2ax_k+b;Po rozwiazaniu tego ukł równań i przyjęciu ukł wsp. w punkcie P(X_p=0,Y_p=0)otrzymuje się:a=Δi/2X_k;b=i₁;c=0;Czyli r. paraboli przyjmuje postac z=Δi/2x_k*x²+i₁x;Wsp. punktu ekstremalnego wynikające z warunków z'_(x)=Δi/x_k*x+i₁=0,

z”_(x)= Δi/X_k>0 lub z”_(x)= Δi/X_k<0 wyznacza się z wzorów:

X_E=-i₁x/Δi;Z_E=-i₁²x_k/2Δi po rozwiązaniu otrzymujemy: X_K=2(i₂d-ΔH_AB)/ Δi ; Z_K=[(i₂d-ΔH_AB)/ Δi](i₁+i₂). Współrzędne X_W,Y_W: X_W=(i₂d-ΔH_AB)/ Δi; Z_W=x_W*i₁; Wzory na obliczenie długości stycznych T₁=[(i₂d-ΔH_AB)/ Δi]*pier(1+i²_i); T₂=(i₂d-ΔH_AB)/ Δi*pier(1+i²₂); odległość WS=(i₂d-ΔH_AB)/4. Parabola stosowana jako krzywa wyokrąglająca załom niwelety musi charakteryzować się odpowiednią krzywizną. Promienie R krzywizny paraboli muszą być większe od promienia minimalnego (R_min) określającego w warunkach technicznych projektowanej trasy. Ogólny wzór na krzywiznę paraboli: R={1+[z'(x)]²}^3/2/|z”(x)|z którego uzyskujemy R_min=2(i₂d-ΔH_AB)/ Δi². Równanie paraboli: Z=[Δ_i²/4(i₂d-ΔH_AB)]x²+i₁x. Równanie to jest określone w praktyce dla projektowanych nachyleń i₁ i i₂ oraz przy spełnionej nierówności i₂d-ΔH_AB≥R_min*(Δ_i²/2). Spełnienie tej nierówności wymaga odpowiedniego doboru stałych punktów A i B przez które ma przejść niweleta trasy. Tyczenie pkt pośrednich paraboli w ukł współ którego pocz znajduje się w pkt P: Xn=2(i₂d-ΔH_AB)*n/k*Δi ; Zn=(i₂d-ΔH_AB)*n²/k² + 2i₁(i₂d-ΔH_AB)/k*Δi gdzie n- kolejny numer pkt, k- liczba odcinków na które podzielono długość d.

5. Metody wyznaczania przemieszczeń pionowych reperów

Reperami odniesienia mogą być repery ziemne a także założone w fundamentach budynków. Repery odn. mogą byćsytuowane w grupach (min 3) - jest to sprawdzenie czy któryś z nich nie osiadł. Dwa sposoby wyznaczania przemieszczeń pionowych: 1) na podstawie reperów istniejących (wyrównywanie wysokości) 2) na podstawie uzyskanych przewyższeń (wyrównanie przewyższeń)

Kryterium stałości: dmax = ± 1,4 * μ0 * sqrt(n^0 +n') μ0 = 0,05 ÷ 0,15mm

n^0 - liczba stan. w pomiarze wyjściowym n' - aktualnym

hi^0 Δh1 = (hi' - hi^0) <= dmax reper nie zmienił położ.

hi' Jeżeli któryś z reperów osiądzie nie będziemy wiedzieć który. Dlatego reperów odniesienia musi być przynajmniej 3. Lepiej żeby było ich 5-6 bo wtedy jeżeli któryś wypadnie to i tak będziemy mogli sprawdzić stałość. Musimy też mieć możliwość sprawdzenia stałości między poszczególnymi grupami reperów. Jeśli coś się nie zgadza potrzebna będzie opinia geologa które repery się poruszyły.

Ad 1) Dobry dla sieci czasowo zmiennych (takich gdzie wypadają repery). Wyrównujemy całą siec reperów w nawiązaniu do któregoś repera -> Hi^0. Inne niezależne wyrównanie Hi^1. ΔHi = Hi^1 - Hi^0. Jeżeli przyjęty reper nie osiadł punkty stałe będą miały ΔH <= dmax. Jeżeli osiadł, wszystko będzie zniekształcone. Przemieszczenia wyzn. poprzez porównywanie wys. rep. co jakiś narzucony z góry czas. W każdym pomiarze wyznaczamy różnicę względem jakiegoś poziomu, który stanowią repery stale.

Ad 2)

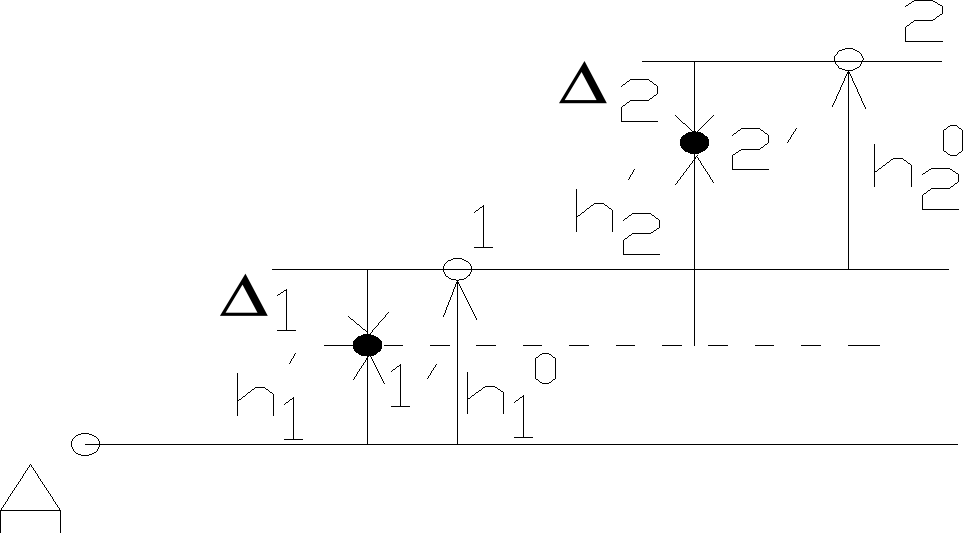
Δ1 = h1' - h1^0 h1^0 + h2^0 = h1' + h2' - Δ2

Δ2 = (h2' - h2^0) + (h1' - h1^0) Δ2 = h2' - h2^0 + Δ1 czyli Δi = Δi-1 + (hi' - hi^0)

Δi - Δi-1 - (hi' + Vi' - hi^0 - Vi^0) = 0

Δi = Δi-1 - (hi' - hi^0) - (Vi' - Vi^0) = 0 VLi = - Δi-1 + Δi - Li

Li = hi' - hi^0 Wzór VLi stosujemy do każdego przewyższenia (dla przewyższeń między reperami stałymi nie) -> dostajemy wiersze macierzy A, wyrazy wolne to - Li , a wagi to pi = 1/(ni'+ni^0) a następnie: X = (AtPA)^(-1) * AtPL

Z tego równania dostajemy od razu przewyższenia. Zaletą w porównaniu do poprzedniego sposobu jest to, że jeżeli przy pomiarze wyjściowym i aktualnym były jakieś błędy systematyczne to część tych błędów powinna się znieść. Wadą jest to że przy sieci czasowo zmiennej, niektóre repery czasem wypadają.

Badanie stałości reperów odniesienia I przypadek: badanie stałości w oparciu o wstępne wyrównanie sieci (dla dużych sieci). Obieramy jeden reper jako odniesienia. Te które są stałe będą miały przewyższenia zerowe (jeżeli nawiązaliśmy się do stałego reperu). (rys: kilka kółek połączonych liniami i koło jednej 100) Δ100 = H100' - H100^0 = 0 (bo przyjęty za stały) Jeżeli przyjęty reper nie będzie stały to okaże sie że nie znajdziemy żadnego stałego. Z wszystkich reperów wybieramy wtedy grupę takich, których przewyższenia pozorne Wi (z kreska u góry) spełniają warunek:

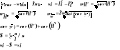
II przypadek: korzystamy z surowych wyników pomiarów otrzymanych w terenie (dla małej ilości reperów np. 6).

Rp	μ0 = 0,1mm	nr Rp
				II	III	IV
I	n^0 + n' dmax h' - h^0

Tabela przewyższeń między reperami (jezeli przekraczają wartość dmax - środkowa wartość. to jeden z reperów jest ruchomy). Możemy mu wyznaczyć przewyższenie. dmax polega na tym że bierzemy podwójny lub potrójny błąd średni niwelacji, zależy z jakim prawdopodobieństwem chcemy mieć pewność, że te repery się nie poruszą.

Przemieszczenia: a) bezwzględne - układ odniesienia jest stały b) względne - mając budynek, na którym są repery przyjmujemy jeden z nich za stały i w stosunku do niego mierzymy osiadanie pozostałych. Jeżeli nie dowiążemy reperu przyjętego za stały do jakiegoś reperu odniesienia, nie będziemy wiedzieć ile cały budynek osiadł. Dostaniemy jedynie informacje o tym ile każdy z reperów na budynku osiadł w stosunku do tego przyjętego

7.Procedura postępowania przy tyczeniu pkt w przestrzeni metodą swobodnego stanowiska.

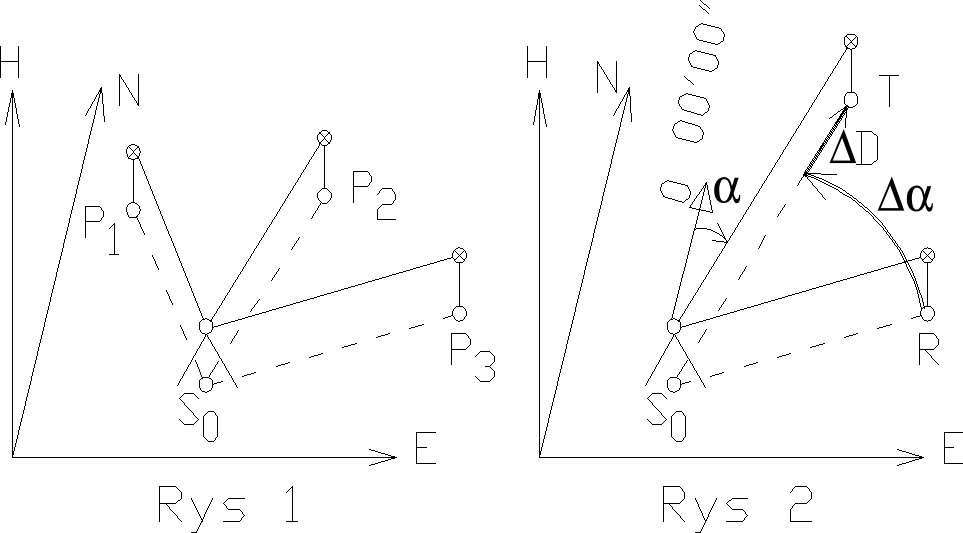
(Rys 1) Wyznaczenie współrzędnych stanowiska bezpośrenio w terenie oparte jest najczęściej na wykorzystaniu znanej konstrukcji wcięcia wstecz. Odpowiednie programy pozwalające na rozwiązanie tego zadania są instalowane obecnie w większości tachymetrów elektr. Pozwalają one na wyznaczenie wspoł. przestrzennych stanowiska (N0, E0, H0) z wykorzystaniem obserwacji liniowych, kątowych lub kątowo-liniowych do odpowiednio licznej grupy punktów odniesienia Pi (Ni , Ei , Hi).Wsp. pkt odniesienia powinny być zmagazynowane w archiwum współrzędnych pamięci tachymetru lub będą wprowadzane z klawiatury instrumentu. Korzystanie z tych programów wymaga wprowadzane nr stanowiska i wys. instr. hi. Następnie celuje się na kolejne pkt-y odniesienia wywołując z archiwum współrzędne pkt przez wprowadzenie do programu ich oznaczeń. Wycelowanie na każdy pkt odniesienia łączy się z wprowadzeniem wysokości reflektora hr i wykonaniem odpowiednich obserwacji. Po wykonaniu obserwacji do ostatniego punktu odniesienia zostaną wyświetlone ostateczne wyniki obliczeń współrzędnych stanowiska N0 , E0 , H0. Mogą one być przeniesione do archiwum współrzędnych. Jeśli współrzędne st. uzyskano z wcięć dostarczających obserwacji nadliczbowych, wówczas program pozwala na obliczenie parametrów charakteryzujących dokładność sytuacyjnego i wysokościowego wyznaczenia położenia stanowiska.

Tyczenie. Ze swob. stan. wykonujemy tyczenie metodą biegunową (najpowszechniej stosowaną w procesach tyczeniowych ok 80%) stąd tez odpowiednie programy ułatwiające przygotowanie danych do tyczenia instalowane są we wszystkich typach tachymetrów elektronicznych. Współrzędne stan. oraz jego orientacja są juz w pamięci instr. po wykonaniu programu Swobodne stanowisko. Można zatem przejść do tyczenia. Po wprowadzeniu numeru punktu tyczonego T i jego współrzędnych (pamięć instr lub klawiatura) obliczony zostaje azymut i odl. do pkt tyczonego (Rys 2). Tyczenie polega na ustawieniu reflektora w punkcie R i wykonaniu obserwacji kąta poziomego i odległości. Wówczas wyświetlona zostaje różnica Δα pomiędzy kątem obl. ze wsp. pomierzonym oraz różnica ΔD pomiędzy pomiędzy odl. obliczoną ze wsp. i pomierzoną. Przesuwanie pryzmatu wywoływać będzie zmiany wyświetlanych różnic Δα i ΔD. Punkt T zostanie wytyczony, gdy obydwie wymienione różnice osiągną wartość zero. Następnie przechodzimy do wysokościowego tyczenia punktu T. Zgodnie z procedurą programu zainstalowanego w tachymetrze wprowadzamy wysokość instr. hi w celu wyznaczenia wys. osi obrotu lunety oraz wys. hr pryzmatu. Tyczenie wysokościowe polega na ustawieniu pryzmatu w punkcie T i wykonaniu pomiaru odl. i kąta pionowego, na podst. których obliczona zostanie aktualna wysokość pkt. T oraz różnica pomiędzy wys. projektowaną a aktualną Podnosimy lub opuszczamy pryzmat aż wartość tej różnicy wyniesie 0.

8.Tyczenie wysokościowe: (rysunek: niwelator, dwa punkty po obu stronach P, R; dwie łaty z odczytami P i W) Wyznczenie wysokości pkt. metodą niw. geometrycznej polega na odłożeniu różnicy wysokości Δz pomiędzy reperem odniesienia R a punktem tyczonym P, uzyskanej wg wzoru Δz = Zp - Zr. Praktyczna realizacja tego zalecenia w pracach związanych na przykład z wyznaczeniem wysokości „zera budowlanego” polega na jednostanowiskowym przeniesieniu wysokości z reperu roboczego R na punkt tyczony. Zatem realizuje się odczyt wprzód na łacie ustawionej w punkcie P obliczany ze wzoru: p = Zr - Zp + w. W innych przypadkach konieczne jest poprowadzenie ciągu niwelacyjnego i bieżące sumowanie przewyższeń uzyskiwanych na kolejnych stanowiskach. Użycie elektronicznego niwelatora kodowego rozwiązuje problem prowadzenia obliczeń w terenie przez zastosowanie odpowiedniej procedury rejestracji wyników obserwacji.

9.Łuki koszowe.

Łuk koszowy składa się z następojących po sobie łuków o różnych promieniach zakrzywionych w tym samym kierunku.

Obliczenia łuku koszowego o dowolnej liczbie promieni prowadzi się w oparciu o trzy warunki.(dla łuku składający się z trzech łuków kołowych):

1. α1+ (180⁰+ α2) + (180⁰+ α3)+90⁰+ (180⁰- α)+90⁰=(n-2)*180⁰ →∑ αi= α 2. T1= (R1-R2)sin α1+(R2-R3)sin(α1+ α2) +R3sin(α1+ α2+ α3)+T2cosβ 3. R1=(R1-R2)cosα1+(R2-R3)cos(α1+ α2) +R3cos(α1+ α2+ α3)+T2sinβ

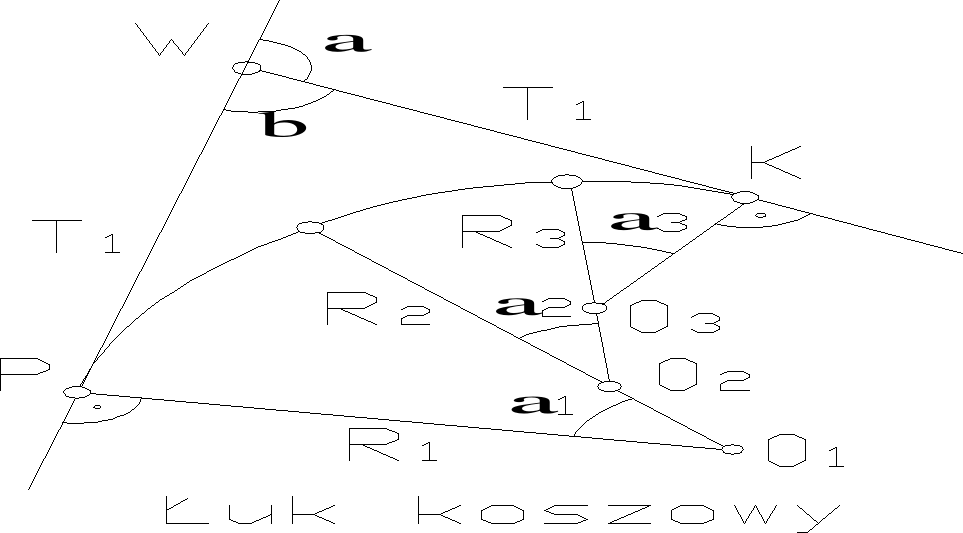
Łuk koszowy składający się z dwóch łuków kołowych(najprostszy)

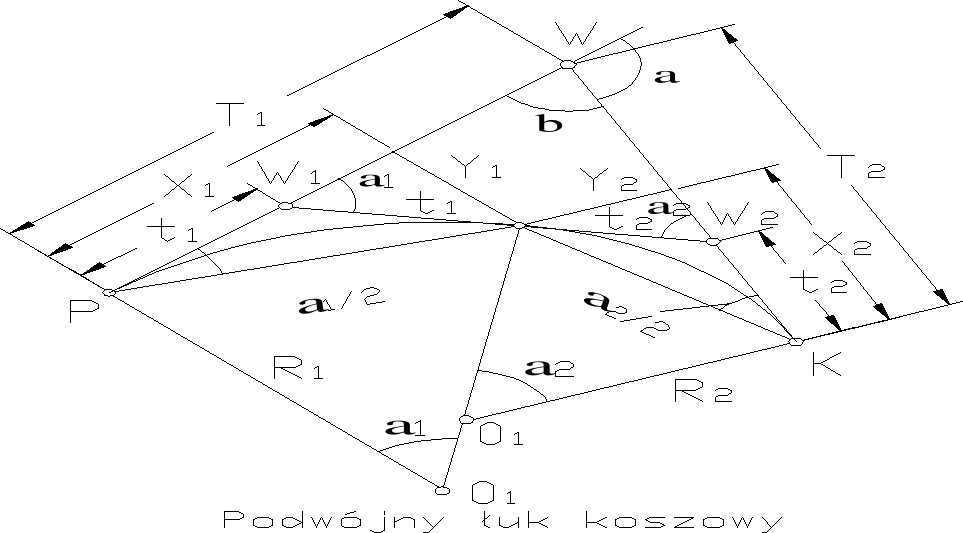
Elementami geometrycznymi wyznaczającymi podwójny łuk koszowy są: -długości stycznych głównych (T1,T2)- promienie łuków kołowych(R1,R2)

-kąt zwrotu stycznych głównych (α)- kąty środkowe łuków kołowych(α1 α2) Aby wyznaczyć położenie pkt. głównych P,T,K konieczna jest znajomość czterech z siedmiu wymienionych elementów geom. i obliczenie pozostałych z równań (1,2,3)(dwa zestawy rów.) α1+ α2= α lub α1+ α2= α

4)T1=(R1-R2)sin α1+R2sinα -T2cos α T2=R1sinα-(R1-R2)sinα2-T1cosα 5)R1=(R1-R2)cos α1+R2cosα+T2sin α R2=R1cosα-(R1-R2)sinα2+T1sinα ; Dwa typowe rozwiązania praktyczne podwójnych łuków koszowych:

I. Znane jest położenie początkowego pkt. P łuku kołowego czyli α1,R1,R2,T1. Pozostałe elementy oblicza się wg wzoru:

cos α2=(T1sin α+R1cosα-R2)/(R1-R2)

cos α1=(R1-T2sinα-R2cosα)/(R1-R2) lub α- α2= α1

T2 wylicza się ze wcześniejszych wzorów(4)

II.Jeśli dane są α1,T1,T2,R1 to: R2=(1/sin α2)[T2+R1(sin α2-sin α)+T1cos α] ; R2=[1/(1-cosα2)][R1cos α+T1sin α-R1cos α2]po porównaniu równań mamy sin α2[R1(1-cos α)+T1sin α]+cos α2[R1sin α-T2-T1cos α]-(R1sin α-T2-T1cos α=0

Oznaczając wyrażenie w [] odpowiednio AiB mamy:

Asin α2=B(1-cos α2) lub Asin(α2/2)cos(α2/2)= Bsin²(α2/2)→tg(α2/2)=A/B ; Po obliczeniu α2 można obliczyc α1: α- α2= α1 ; Przy założonych oznaczeniach wzór na R2 ma postać:R2=R1-B/sin α2

10. Procedura tworzenia macierzy wariancyjno - kow. wsp. pkt. Q tyczonego metodą swob. stan. z uwzględnieniem błędów osnowy real.

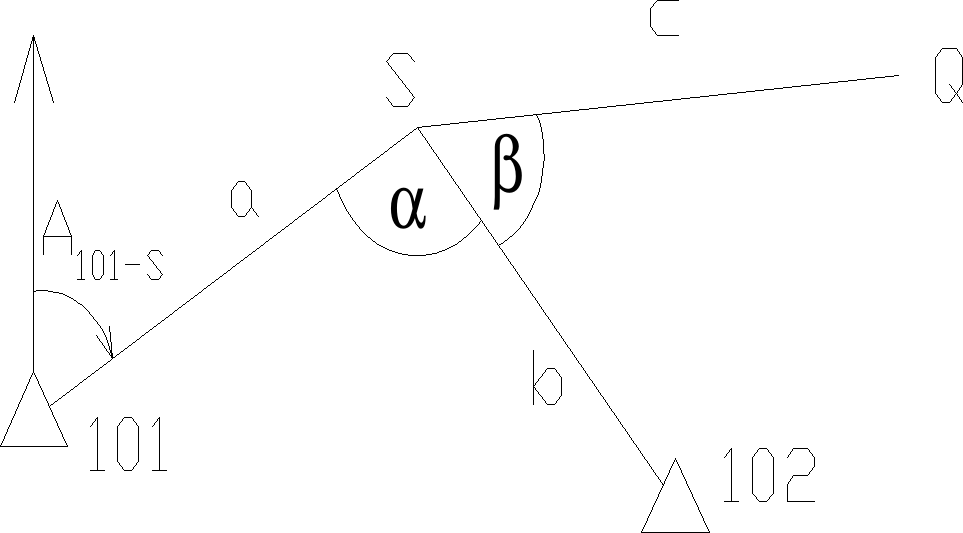
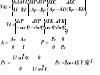
Wybieramy z niej macierz Qc odnoszącą sie tylko dla punktów tyczonych. Macierz Qr = (ArT Pr Ar)^(-1) ujmuje tylko niedokładność (wpływ) tyczenia. Można oddzielić wpływ błędów osnowy i wpływ błędów ralizacji: cov(Xs,Ys) = cov(x,y,X,Y) - cov(Xr,Yr) inaczej Qs = Qc - Qr. Jeżeli mamy zadany błąd m^2 = mr^2 + ms^2 , wiemy czym będziemy mierzyć, możemy wyliczyć błąd osnowy ms^2.

11.Zakładanie i wyrównywanie przestrzennych osnów realizacyjnych.

Stosowanie przestrzennych osnów realizacyjnych jest możliwe dzięki tachimetrom elektronicznym, które jednocześnie mierzą kąt poziomy, pionowy i odległość. Tak więc oprócz współrzędnych płaskich umożliwiają wyzn rzędnej wysokości. W tym przypadku niwel geometryczna zastąpiona jest niwel trygonometryczną. Taki rodzaj osnowy można zastosować wówczas gdy niwel tryg zapewnia wystarczająco dokładne wyznaczenie wysok elementu planu realizacyjnego. W praktyce niwelacja ta zapewnia niekiedy wyzn wysokości z dokład do kilku mm na 500m.Trzeba tu zapewnić także odpowiednią dokł wyznacz wys instrumentu oraz sygnału (0.2-0.5mm)

WYRÓWNANIE

-ułożenie równań obserwacyjnych:

a) dla dług przestrzennej

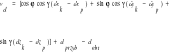
b) dla kątów pionowych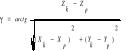

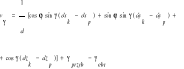
c)dla kąt poziomych(tak jak w płaskiej)

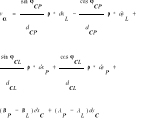
B_L A_L B_P A_P

Układ równań dostosowania ma postać:

v=AX-L gdzie v-to macierz poprawek, A-macierz współ równań X- macierz niewiadomych L-mac wyrazów wolnych

Równania normalne, macierz wagowa P(na podstawie błędów)

V^TPV=min

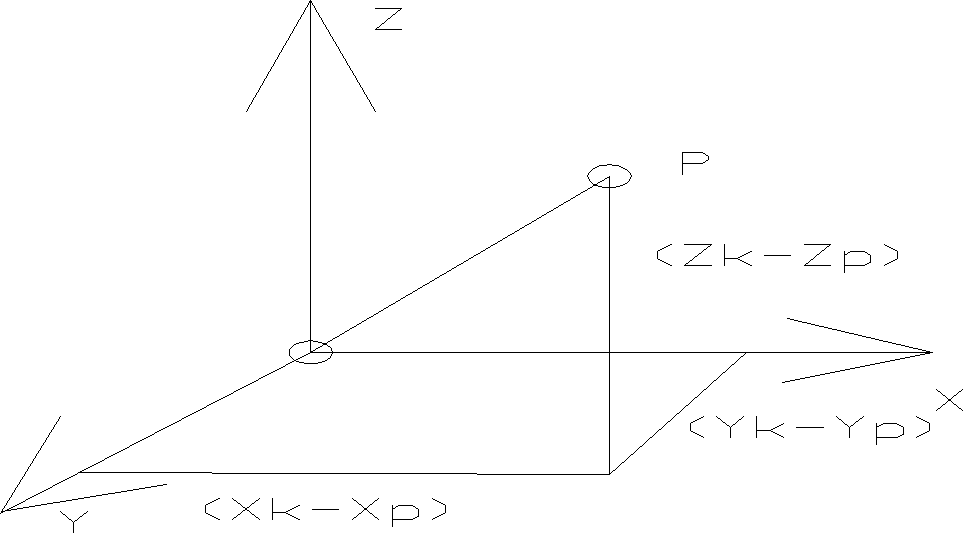
Wyrównane współrzędne:

X=X_przyb+dx

Y=Y_przyb+dy

Z=Z_przyb+dz

Ocena dokładności:

V=AX-L

Cov(X,Y,Z)=
[(A^TPA)^-1]

Przestrzenne osnowy mogą być zakładane za pomocą GPS. Wówczas należy uwzględnić iż jest to pomiar w odniesieniu do elipsoidy WGS84, i należy wprowadzić odpowiednie poprawki w stosunku do układu `'65''

12. Ustalić dokładność tyczenia punktu metodą biegunową z założeniem bezbłędności punktów osnowy realizacyjnej(wyrównanie obserwacji zależnych)

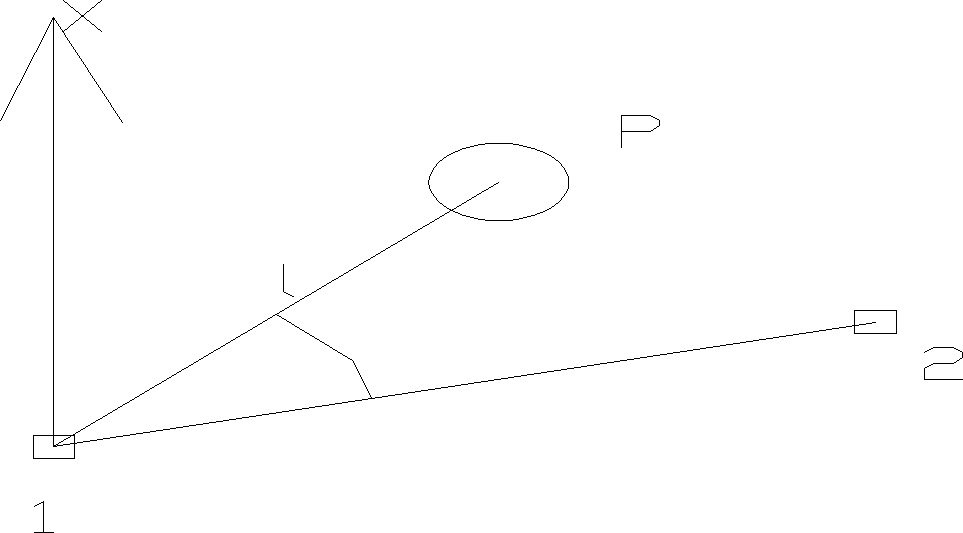
Zestawiamy równania obserwacyjne:

Zestawiamy macierz A, L oraz macierz wag P(z odwrotności błędów)

Dale j obliczamy macierz równań normalnych A^TPA, potem macierz Q=( A^TPA)^-1

V bierzemy z macierzy Q

13. Obliczyć błąd średni wytyczenia punktu 1 metodą biegunową z wykorzystaniem danych przedstawionych na rysunku, z założeniem bezbłędności punktów odniesienia 101,102.

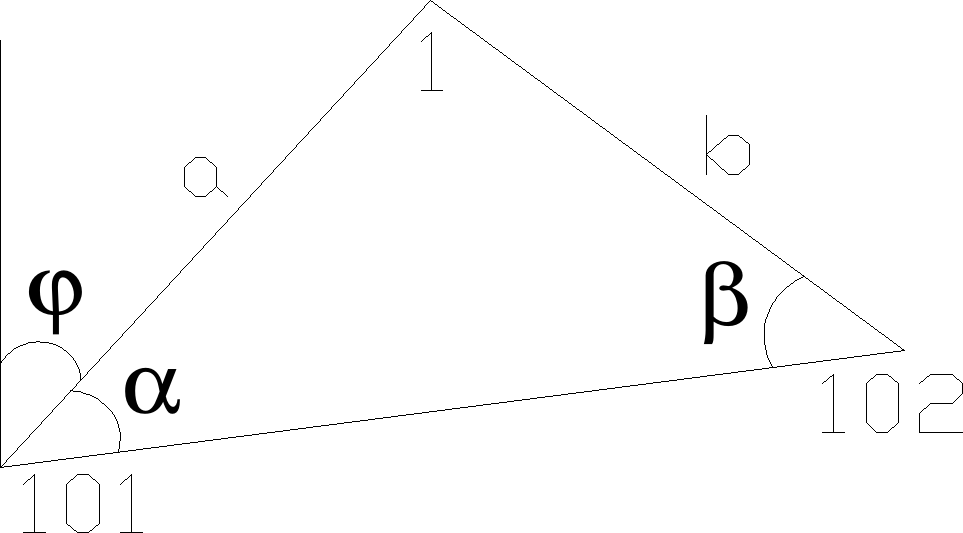
101: 250,200; 102: 280,410; 1:370,300

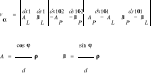
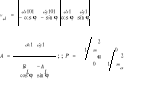
14. Scharakteryzować dokumenty z jakimi geodeta ma do czynienia w procesie tyczenia obiektów budowlanych.

Proces tyczenia obiektów budowlanych podzielic można na dwa etapy:

1)przygotowanie danych niezbędnych do wytyczenia obiektu w terenie(współrz. pkt. tyczonych, dane umożliwiające wytyczenie tych punktów w terenie)

2)tyczenie w terenie

W procesie 1) niezbędne jest zapoznanie się geodety z :

-planem realizacyjnym(mapa w określonej skali, która przedstawi a lokalizację obiektów inwestycji w terenie-możliwość określenia miar do tyczenia )

-normy branżowe, instrukcje geodezyjne, dokumentacja inwestycji: dokumenty te określają dopuszczalne odchyłki współrzędnych punktów wytyczonych od założonych w projekcie, pozwalają wybrać metodę tyczenia uzależnioną od dokładności

- szkice dokumentacyjne, są to szkice obiektów, które należ wytyczyć w terenie(posiadają miary charakterystyczne budynku i stanowią podstawę do wykonania szkiców tyczenia)

W procesie 2) zasadniczo wymagane i wykorzystywane są :

- szkice tyczenia, bardzo zbliżone do szkiców dokumentacyjnych , zapisujemy na nich różnice miedzy elementami niezbędnymi do wytyczenia punktu w terenie a rzeczywistymi miarami uzyskanymi w trakcie tyczenia

- dziennik budowy, dokument , w którym geodeta zapisuje wyniki swoich prac wykonywanych na placu budowy. Jest ona zatwierdzana przez kierownika budowy.

-dziennik prac geodezyjnych-zapisywane są w nim etapy prac geodezyjnych wyknywanych przez geodetę na placu budowy.

15.Scharakteryzować etapy geodezyjnego opracowania planu zagospodarowania terenu sporządzonego na mapie w skali 1:1000

Plan zagospodarownia terenu jest jednym ze składników projektu inwestycji. Skałda się on dwóch części:

-opisowej-graficznej

Część opisową wykonuje się przedstawiając:

- przedmiot inwestycji, istniejący stan zagospodarowania terenu, omówienie przewidywanych zmian w terenie

- zestawienie powierzchni poszczególnych części terenu (powierzchnia zabudowy, dróg parkingów itp.)

- ewentualna informacja o wpisie obiektu do rejestru zabytków, określenie wpływu eksploatacji górniczej, dane o istniejących lub przewidywanych zagrożeniach dla środowiska, zdrowia użytkowników. Cześć graficzną wyznacza się w następującej kolejności:- przygotowanie odpowiedniego rodzaju mapy do celów projektowych(kopia mapy zasadniczej lub w przypadku jej braku mapy jednostkowej) - wybór odpowiedniej skali mapy (np. 1:1000 dla celów związanych z zespołami obiektów budowlanych oraz terenów budownictwa przemysłowego) - naniesienie ma mapę do celów projektowych orientacji położenia inwestycji w stosunku do stron świata, zaznaczenie granicy inwestycji, ukształtowanie terenu z zaznaczeniem zmian w stosunku do stanu istniejącego, układ sieci uzbrojenia terenu, itp.

16. Jak ustala się dokładność tyczenia jeśli znana jest dopuszczalna odchyłka budowlana Dl.

Odchyłka budowlana jest graniczną niedokładnością prac budowlanych i prac życzeniowych.

Spełniona powinna być zależność:

dL_t+dL_b<=dL gdzie dL_t-gran odchył tycz dL_b-gran odchył wykonania prac budowlanych; dL_t²+dL_b²=dL² przy założeniu na dwie równe części to dL_t=dL_b=0,7dL; Można przyjąć że dL_t­<=KdL 0,4 <=K<=1,0 , 0,4 dla tyczenia obiektów o wysokim stopniu ważności , 1,0 dla mniej ważnych obiektów(mniejsza dokładność) Graniczna odchyłka tyczenia odpowiada granicznemu błędowi tyczenia czyli: M_t=dL_t=dl; Graniczny błąd tyczenia można określić z zależności M_t=r*m_t gdzie m_t to błąd tyczenia, a r to współczynnik którego wartość zależy od wyznaczanego prawdopodobieństwa nieprzekroczenia błędu granicznego (2<=r<=3).Ostatecznie mamy: m_t≤KdL/r

Ustalony średni błąd tyczenia m_t daje podstawę do analizy dokładności prac życzeniowych wg zależności m_t²=m_r²+m_s²

m_r- średni błąd tyczenia z tytułu niedokładności metody realizacji, m_s- średni błąd tyczenia z tytułu niedokładności osnowy realizacyjnej Dalsza analiza może prowadzić do ustalenia dokładności tyczenia danych punktów, a co z jest tym związane to do wyznaczenia metody tyczenia. Można również określić metodę i sprzęt, jakim należy określić osnowę realizacyjna(ilość serii, sprzęt pomiarowy,itp)

17.patrz 9 łuki koszowe

18. Na czym polega geodezyjne opracowanie projektu zagosp. terenu lub działki.

Polega na wyznaczeniu współrzędnych punktów tyczonych u układzie współrzędnych geodezyjnych osnowy.Trzy etapy: 1.wyznaczenie współrzędnych punktów reprezentujących treść projektu w układzie lokalnym O'x'y' 2.obliczenie współczynników transformacji układu z lokalnego do terenowego 3.wyznaczenie współrz punktów tyczonych w ukł.terenowym.

ad 1) Należy przyjąć na planie początek ukł.współrzędnych O' oraz oś O'x'. W oparciu o przyjęty układ współrz. oraz wyszczególnione na planie warunki geometryczne i wymiary oblicza się współrz. punktów.

ad 2) Wariant A: nadanie początkowi układu lokalnego O' współrzędnych, a osi O'x' azymutu-obliczonych bezpośrednio w układzie osnowy geodezyjnej Oxy (terenowym).Wariant ten prowadzi bezpośrednio do wyznaczenia współrzędnych punktów tyczonych w ukł.terenowym. Wariant B: Transformacja przy zastosowaniu wzorów: x=x₀+x'cosy'sin  y=y₀+x'siny'cos Przy zastosowaniu większej liczy punktów dostosowania równania aproksymujące, wg których można wyznaczyć współczynniki transformacji mają postać: Vx_i= x₀+x_i'cosy_i'sinx_i ;

Vy_i= y₀+x_i'siny_i'cosy_i. Wartośc kąta skrętu układów obliczmy z wzoru: ₀=arctg(sin cos. Dokładność wpasowania obydwu układów charakteryzuje odchylenie standardowe:
.

Ad 3)Wykorzystujemy obli. parametry transformacji x₀, y₀, 

Wysokości punktów podawane są zazwyczaj w odniesieniu do przyjętego w kraju poziomu odniesienia i nie wymagają przeliczeń.Są realizowane w dowiązaniu do punktów państwowej osnowy wysokościowej lub dowiązanych do nich reperów roboczych,stanowiących sieć punktów usytuowanych na terenie inwestycji.Wys. wszystkich punktów wyznaczane są w systemie wysokości normalnych.

19. Przedstawić procedurę tyczenia punktów gł i pośr. PIONOWEGO ŁUKU KOŁOWEGO

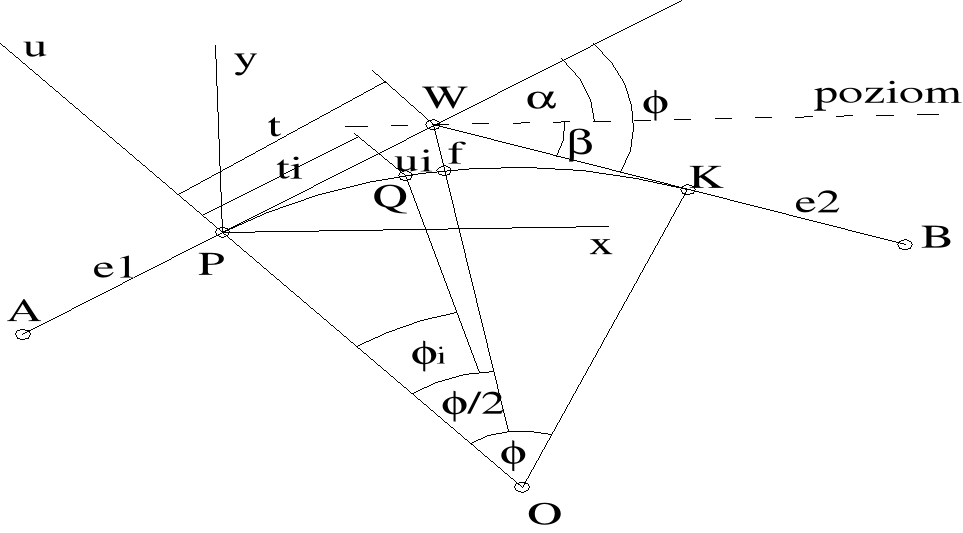
t=R*tg(/2) lub t=R*tg[(±)/2]. Ponieważ  i  to małe kąty przyjmujemy: tg[(±)/2 = 0.5*tg(±, więc ost.

.Stosując uproszczenie tg*tg≈ 

mamy t=R/2*( tg±tg Zastępując nachylenia sąsiednich odcinków niwelety spadkami tych odcinków: tg=e₁; tg=e₂ otrzymujemy wzór t=R/2*|e₁-e₂|. 2.Obliczenie odległości WS=f ze wzoru: f=t²/2R=R/8*(e₁-e₂)² 3. Określenie wysokości punktów głównych z_P=z_w-t*e₁ ; z_K=z_w+t*e₂ ;

z_S=z_w-f. Przygotowanie danych do lokalizacji punktów POŚREDNICH: 1. Określenie odległości t₁ 2. Określenie wysokości na łuku wypukłym z_i=z_p+e₁*t_i-u_i lub wklęsłym z_i=z_p+e₁*t_i+u_i , gdzie u_i=t_i²/2R traktowane jako różnicę wysokości. Wysokie wymagania dokładnościowe w kształtowaniu pionowych łuków kołowych narzucają obliczanie współrzędnych punktów pośrednich Q w układzie t, u stosując wzory: t_i=R*sin ; u_i=2R*sin²(_i/2).Transformacja do układu x,z według wzorów: x_i=t_i*cos+u_i*sin  z_i=t_i*sin-u_i*cos

Kolejnym etapem jest wyznaczenie punktów głównych i pośrednich w terenie. Do tego celu należy przygotować niezbędne dane do tyczenia i wybrać metodę tyczenia.

20. Opisać postępowanie przy projektowaniu i tyczeniu ŁUKÓW ODWROTNYCH

Łuk odwrotny składa się z zespołu łuków kołowych zakrzywionych w odwrotnych kierunkach i najczęściej przedzielonych wstawką prostą.Stosuje się je w trudnych warunkach terenowych o urozmaiconej rzeźbie i trwałych przeszkodach,gdy wyokrąglenie załamania trasy za pomocą jednej krzywej jest niemożliwe.

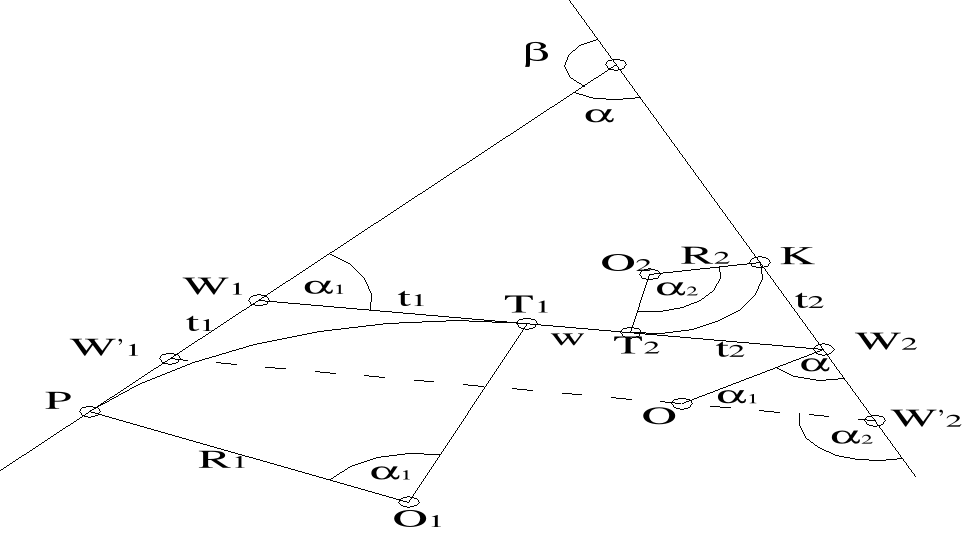
kołowych(t₁+t₂) powiększonej o długość wstawki prostej.

Kierunek wspólnej stycznej wpływa na bezpośrednio na wielkości kątów zwrotu _ _Ostateczne położenie linii W₁W₂ ustala się drogą kolejnych przybliżeń. Obieramy najdogodniejszy przebieg linii i mierzymy jej długość oraz kąty zwrotu _ _ a następnie przyjmujemy promienie R₁ R₂ . Obliczamy długość stycznych t₁ i t₂ ze wzoru : t_i=R_i*tg(_i/2) oraz długość W₁W₂= t₁+t₂+w. Jeżeli obliczona długość ta jest za krótka lub za długa to można wspólną styczną przesunąć równolegle do właściwego położenia, np: W'₁W'₂.Szukane przesunięcie otrzymujemy poprzez rozwiązanie trójkąta; OW₂W'₂ bo znane są w nim wszystkie katy i długość OW'₂. Zamiast przesuwać linię W₁W₂ można założyć jej niezmienność dopasowując wartości promieni R₁ R₂ aby było spełnione równanie W₁W₂= t₁+t₂+w lub też przyjąć odpowiednie długości stycznych t₁ i t₂ obliczając promienie ze wzoru t_i=R_i*tg(_i/2).

w przypadku gdy ustalony jest promień R₁ oraz kąt zwrotu stycznych zasadniczych , to po wyznaczeniu przebiegu stycznej W₁W₂ mierzy się jej długość i kąty zwrotu _ _, a następnie oblicza promień R₂ ze wzoru

R₂=(W₁W₂ - R₁*tg(₁/2))*ctg(₂/2)

21.Scharakteryzować treść planu zagosp sprządzonego przez projektanta i przedstawienie danych do tycz obiektów w oparciu o osnowe geodezyjną

Część opisowa określa: 1.przedmiot inwestycji, a także zakres całego zamierzenia i kolejność realizacji obiektów,istniejący stan zagosp działki lub terenu. 2.projektowane zagospodarowanie (urządzenia budowlane, układ komunikacyjny,sieć uzbrojenia,ukształtowanie terenu) 3.zestawienie powierzchni wszystkich fragmentów projektowanej działki lub terenu 4.informacje z MPZP 4.dane wynikające ze spec. i charakteru obiektu bud.

Część rysunkowa: 1.granice działki lub terenu, sytuacyjne i wysokościowe usytuowanie obiektów istniejących, wymiary, wzajemne odległości obiektów i urządzeń,wysokości charakterystycznych punktów obiektu i terenu, strefy ochronne. 2.układ komunikacji wewn (drogi, bocznice kolejowe, place, itp.) 3.ukszt terenu i zieleni 3. układ sieci uzbrojenia terenu (wodociągowa, gazowa, cieplna, kanaliz, telekcom, elektr). Dla dużych inwestycji projekt zagosp.terenu może być przedst.na oddzielnych rysunkach ujmujących wybraną tematykę (budynki, komunikacja, sieć uzbrojenia terenu, itp.) Zgodnie z wymogami Pr.Budowl.,tyczenie obiektów budowlanych należy wykonać w odniesieniu do osnowy geodezyjnej,dlatego treść przedstawioną przez projektanta należy uzupełnić o punkty osnowy geoid. oraz współrz. punktów osnowy i punktów reprezentujących obiekty bud. Ostatecznie plan realizacyjny zawiera treść składającą się z: 1.granice terenu inwestycji 2.granice strefy ochronnej 3.granice robót ziemnych (wydzielonych rejonów ,tarasów, skarp, rowów) 4.obiekty i urządzenia istniejące 5.obiekty projektowane (obrysy, osie główne, elem.charakt, nazwy),wymiary obiektów, rozstawy osi, odległości między obiektami proj i istniejącymi 6.sieć uzbrojenia terenu 7.osie torów kolejowych, rozjazdy, skrzyżowania, urz.techn i towarzyszące obiekty inż. 8.charakt. punkty osi i korony drogi, skrzyżowania dróg, urz.techn i towarzyszące obiekty inż. 9.osie i linie brzegowe cieków i zbiorników wodnych, linie zalewowe, wodne bud. inż. 10. współrzędne płaskie załamania granic, obrysów osi, punktów głównych i chartka. obiektów 11. wysokości punktów wyznaczających poziom zerowy obiektu bud.,wys. chartka. punktów pionowego uksztł. terenu 12.punkty istniejącej i projektowanej osnowy geodezyjnej,współrzędne i oznaczenia.

PRZEDSTAWIENIE DANYCH: Szkic dokumentacyjny przygotowany na podstawie planu realizacyjnego zawiera: 1. szkic obiektu lub fragmenty bez obowiązku zachowania skal 2.istniejące przewody i urządzenia podziemne 3.punkty osnowy geodezyjnej 4.współrzędne punktów osnowy i punktów tyczonych 5.obliczone dane do tyczenia i miary kontrolne 6. nr zlecenia i oznaczenie dokumentacji 7.nazwisko wykonawcy i data.

Na kopii szkicu robi się szkic tyczenia, na którym są wszystkie dane liczbowe uzyskiwane podczas tyczenia wraz z miarami kontrolnymi.

22. biegunowa metoda tyczenia punktów pośrednich klotoidy 
Punkty pośrednie klotoidy rozmieszcza się na ogół w równych odległościach łuku ΔL, przy czym odległości te mogą być wartościami okrągłymi (10m, 20m), lub nieokrągłymi dostosowanymi do przyjętego w tablicach klotoidy odstępu ΔL argumentu l. Odległość między punktem O ( przegięcia klotoidy) a dowolnym punktem na klotoidzie można określić wzorem Li=i*ΔL lub Li=ΔLi+(i-1) ΔL dla ustalonego parametru a klotoidy oblicza się wartości argumentów li=Li/a i odczytuje z tablic współ Xi i Yi

potrzebne do tyczenia pkt pośr klotoidy od stycznej gł. uzyskuje się

Xi=xi*a ; Yi=yi*a. Tyczenie punktów m. biegunową: przyjmując biegun w punkcie przegięcia O punkty pośrednie można tyczyć przez odłożenie od stycznej głównej kąta kierunkowego ωi i odległości Ci.

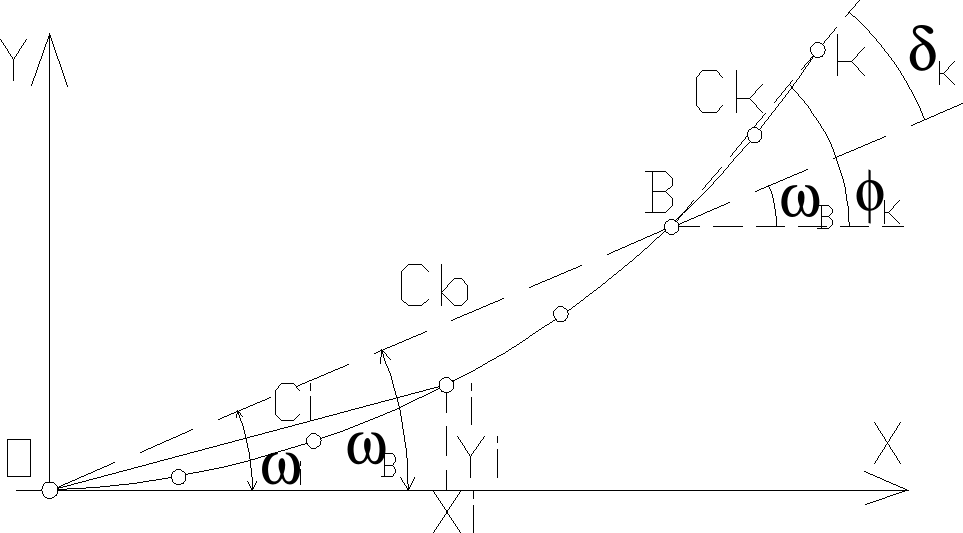
ωi=arctg(Yi/Xi) Ci=pier*(Xi²+Yi²) ; Xi,Yi-odczytujemy z tablic, a-ustalone. Kąt kierunkowy ωi można również odczytać bezpośrednio z tablic klotoidy jednostkowej. Jeśli tyczenie całego łuku klotoidy z punktu O jest utrudnione, wówczas stanowisko tachymetru można usytuować na dowolnym, już wytyczonym punkcie pośrednim B. Kąt δ_K=φ_K-ω_B pomiędzy przedłużeniem cięciwy OB. A kierunkiem do kolejnego punktu pośredniego k. Odległość C_K punktu k od nowego bieguna B: C_K=pier[(X_K-X_B)²+(Y_K-Y_B)²]

23.Przedstawić sposoby tyczenia punktów pośrednich płaskiego łuku kołowego met. biegunowa.

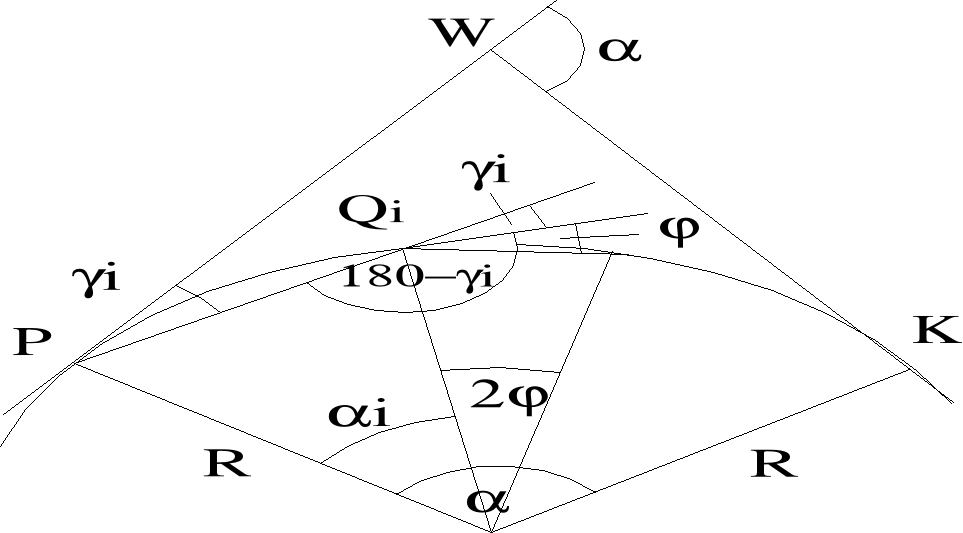
Przygotowanie danych: ustalenie wielkości kąta środkowego 2 odpowiadającego przyjętej wartości L długości odcinka łuku. Kąt oblicza się ze wzoru: 2L/R*ρ. Jeżeli łuk PSK podzielono na n równych części: 2n. Tyczenie punktów pośrednich Q_i z punktów głównych głównych lub K polega na odłożeniu od stycznej głównej kąta γ_ii długości c_i. Ponieważ _i=i(2) zatem γ_i= i*. Długość c_i=2R*sin(_i/2)=2R*sin(i*). Stanowisko pkt P i K:Kolejne punkty Q_i tyczymy korzystając z kątów γ_i i cięciwy c łączącej dwa sąsiednie punkty pośrednie kt przyjmuje wartość c=2R*sin. W tym celu po wytyczeniu punktu Q_i-1 odkłada się z punktu P kąt γ_i, zaś z punktu Q_i-1 cieciwę c uzyskując w przecięciu szukany punkt pośredni Q_i. Stanowisko pkt S: podobna procedura jak wyżej tylko ze kąty kierunkowe γ_i odkłada się od stycznej pomocniczej W₁W₂.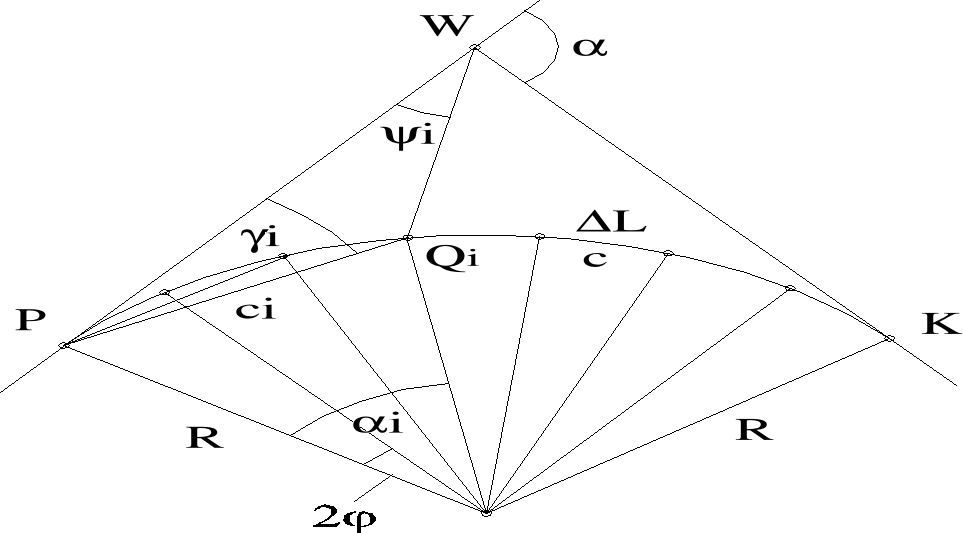

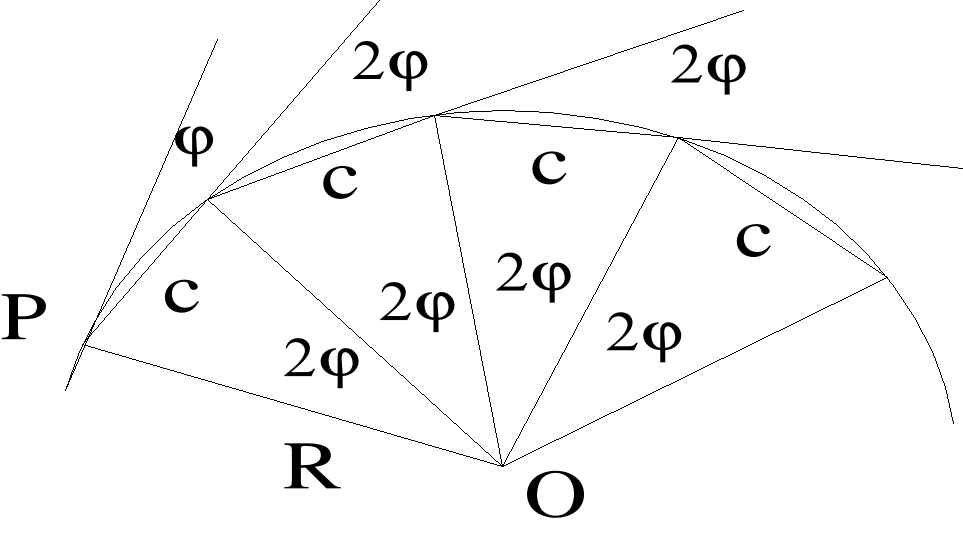
Stanowisko punkt osnowy: tyczenie w oparciu o współrz. punkt osnowy i pośrednich,obliczone w procesie geodezyjnego opracowania projektu technicznego trasy.

24.Tyczenie pkt głównych łuku kołowego:

Łuk kołowy

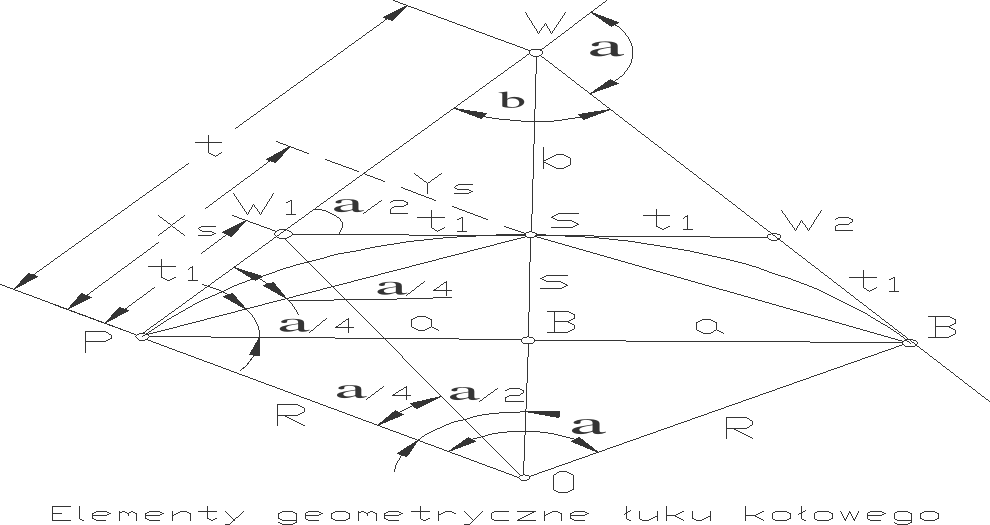
W projektach technicznych łuk taki powinien być określony przez dowolne dwie wielkości z :R-promień łuku kołowego,α-kąt zalamania trasy,L-długość łuku kołowego,t- długość stycznej głównej. Do pkt. głównych łuku należą pkty P,K,S. Aby możliwe było wytyczenie pkt głównych należy obliczyć następujące wartości:

1) t=PW=KW=Rtg(α/2)-długość stycznej głównej

2) b=WS=R(sec(α/2)-1)-odległość wierzchołkowa

3) a=PB=BK=Rsin(α/2)-długość połowy cięciwyPK

4) s=BS=R(1-cos(α/2))-długośćstrzałki

5) t1=PW1= Rtg(α/4)-długość stycznej pomocniczej

6) L= (R α )/ρ- długość łuku kołowego

7) PS=2Rsin(α/4)-długość cięciwy dla połowy łuku

8) xs=PScos(α/4)= Rsin(α/2) → xs=a -odcięta pkt środkowego

9)ys=PSsin(α/4)=2Rsin²(α/4) → ys=s-rzędna pkt środkowego S

Tyczenie pktgłównych przy dostępności wierzchołka W:

Wyznaczenie P i K polega na odłożeniu od W długości t wzdłuż obydwu ramion kąta β. Pkt S można wytyczyć nast. Metodami:

-biegunową z pkt W przez odłożenie długości b wzdłuż dwusiecznej β

-biegunową z pkt P lub K po odłożeniu kąta α/4 i dł. Polub KS

-ortogonalną od stycznej PW przez odłożenie a i s-liniową przez odłożenie od pkt Pik długości st. pomocniczej t1 wzdłuż lini PW i KW oby otrzymać W1iW2 potem odłożyć t1 wzdłuż W1W2 i otrzymamy

Tyczenie pktgłównych przy niedostępności wierzchołka W:

Dla ustalenia wielkości kąta zwrotu stycznych α stosuje się pomocnicze konstrukcje geometryczne:

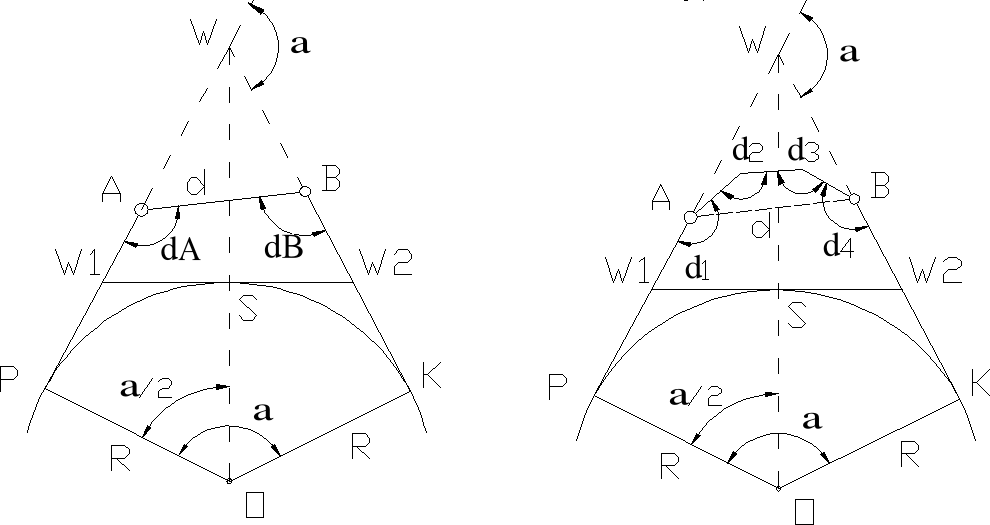
W takim przypadku proste odcinki trasy powinny być odtworzone z dowiązaniem d osnów geodezyjnych lub szczegółow terenowych.Na tych prostych obiera się pkt AiB tak ażeby można je było połączyć jadnym lub kilkoma odcinkami tworzącymi ciąg poligonowy w którym dokonuje się pomiaru kątów i długości boków.Następnie dokonuje się niezbędnych obliczeń:

Przyp1 Przyp2

1) α = 360⁰-(δA+δB) α=(n+1)180⁰-Σδ

długość AB= d otrzymuje się z rozwiązania

poligonu w dowolnym układzie lokalnym

2). PW=KW=Rtg(α2) 3). AW=d*(sin δB/sin α) 4). AW=d*(sin δA/sin α) 5). AP=PW-AW 6). BK=KW-BW.

Tyczenie P i K odbywa się poprzez odłożenie odległości AP i BK odpowiednio od pkt. A i B wzdłuż obydwu prostoliniowych odcinków trasy. Pkt S tyczy się tak jak wcześniej .

25.Przedstawić czynności geodezyjne przy formowaniu nasypów i wykopów drogowych.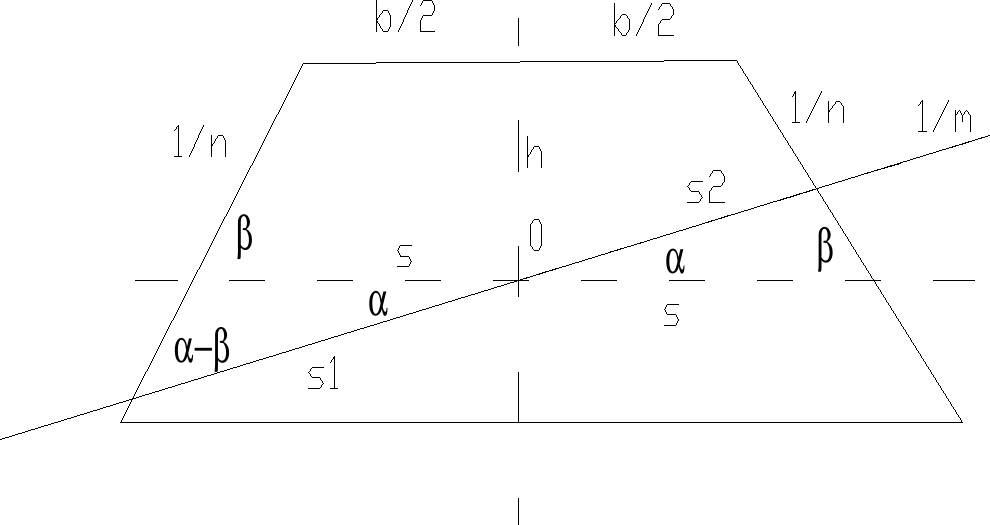

B-szerokość korony nasypu/wykopu;h-wysokośc nasypu/wykopu;

n-mianownik nachylenia skarpy.

Tyczenie polega na wyniesieniu w teren osi podłużnej wznoszonej budowli oraz przebiegu krawędzi przeciecia zboczy nasypów lub wykopów z powierzchnią terenu, a także wskazanie wysokościowego położenia wyodrębnionych fragmentów budowli. Nalezy w terenie utrwalic projektowane kształty przekrojow poprzecznych usytuowanych w odległościach zapewniających poprawne formowanie budowli ziemnej.W terenie o jednolitym nachyleniu określenie położenia śladów przecięcia skarpy z powierzchnia terenu polega na odlozeniu od punktu 0 odleglosci s1 i s2 obliczonych ze wzorow: s=b/2+h*n;s1=s*sinβ/sin(β-α);s2=s*sinβ/sin(α+β)

Do ustawiania skarp można uzyc tzw. Skarpownikow(rys poniżej-ciagla linia)

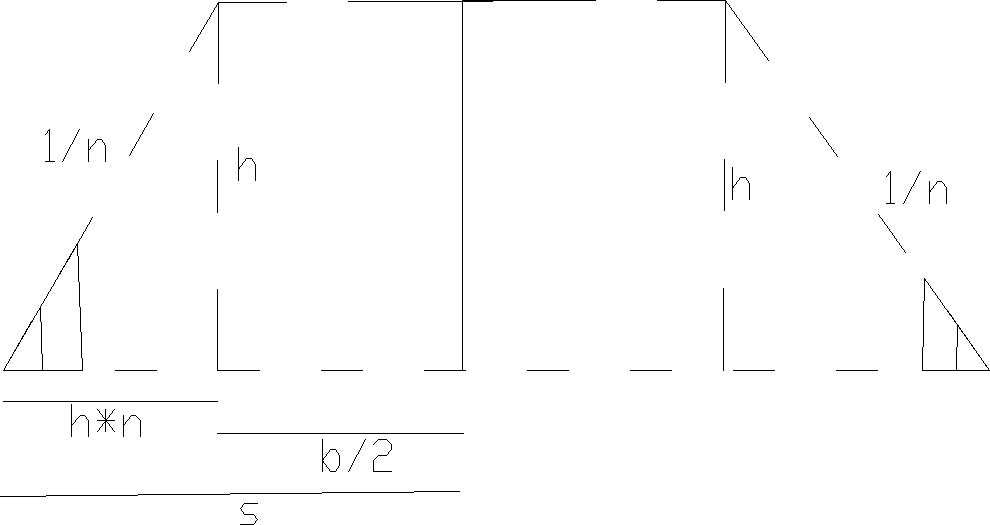
przygotowanie danych do tyczenia podstawy ziemnej w wykopie prowadzi się w sposób analogiczny jak przy tyczeniu nasypu, tylko ze s wyliczamy ze wzoru s=b/2+h1*n1+d+(h+h1)*n

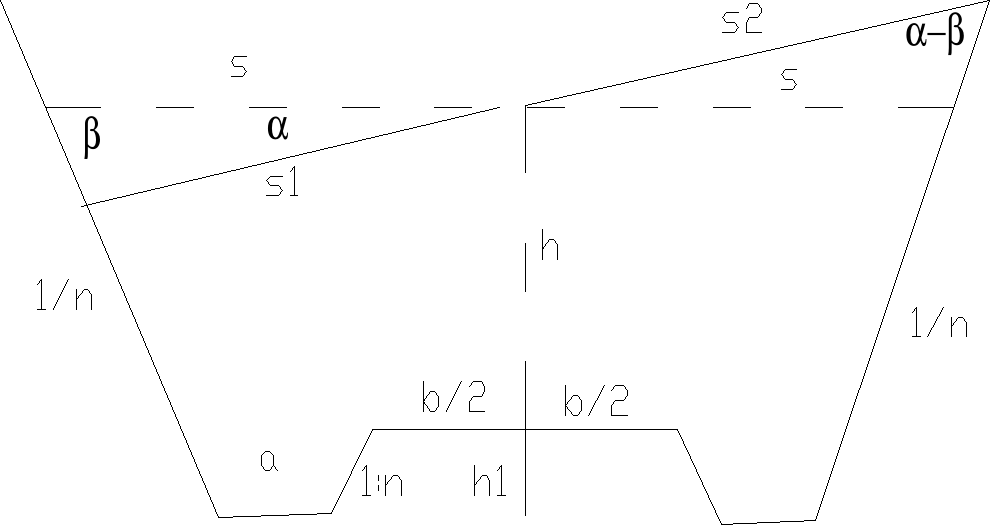
Nasypy mogą być formowanie stopniowo:

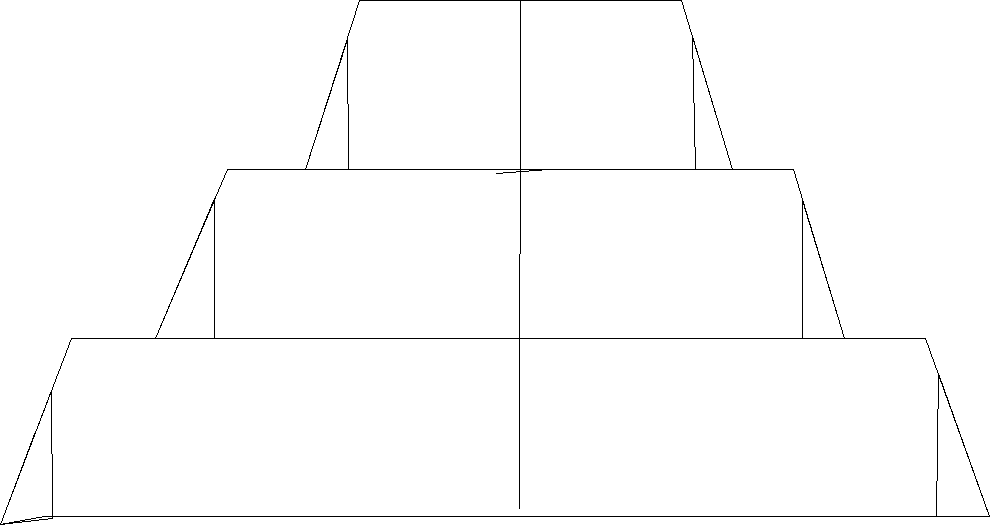
Prace życzeniowe prowadzone przy wznoszeniu obiektow SA zazwyczaj wielokrotnie powtarzane w miare postępów prac ziemnych. Ostateczny kształt wzniesionej budowli dokumentuje się po wykonaniu pomiarow inwentaryzacyjnych. Uzyskuje się wówczas możliwość sprawdzenia stopnia zgodności kształtu i rozmiarow wzniesionej budowli z założeniami projektowymi.

Na podst. tej grupy reperów znajdujemy

S - przesunięcie poziomu odniesienia

wi - przesunięcie prawdziwe

Dysponując tymi trzema równaniami można wyznaczyć tylko 3 niewiadome, natomiast inne wielkości występujące w równaniach muszą być pomierzone w terenie lub zostać założone w projekcie

1. Wyznaczenie macierzy war-

kowar. dla S - zest. równ obser.

A = ρ * cos A / dlug

B = ρ * sin A / dlug

Vx1 = dx1 Vx2 = dx2

Vy1 = dy1 Vy2 = dy2

Macierz równań obserwacyjnych:

Szukamy (AtPA)^(-1)

Ujmuje ona wpływ

osnowy i tyczenia dla pkt: osnowy i tyczonych

Przygotowanie danych do lokalizacji punktów GŁÓWNYCH (P,S,K). 1.Obliczenie długości stycznych PW=WK=t według wzoru:

Kształt łuku odwrotnego uzależniony jest od kierunku i długości stycznej W₁W₂ obydwu łuków kołowych. Długość tej stycznej musi być równa sumie stycznych obu łuków

Stanowisko pkt W: Okładamy kąt _i=arcsin(c_i/d_i*sinγ_i) i długość d=sort(t²+c_i²-2t*c_i*cosγ_i).Wzory uzyskujemy poprzez rozwiązanie trójkąta PWQ.

Punkt pośredni Q_i jako biegun: Odkładając od cięciwy PQ_i kąty:

(180°-i* (180°-i*

Punkt pośredni Q_i jako stanowisko (metoda wieloboku/poligonu wpisanego): stosowane w warunkach ograniczonej przestrzeni budowy(np.tunele). Odłożenie od cięciwy Q_i-1-Q_i kąta środkowego 2 i odległości c.

---