2. Wstęp teoretyczny
b. Część II - Opory ruchu w rurociągach
Miarą energii mechaniczne przepływające cieczy jest wartość tzw. Trójmianu Bernoulliego:
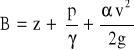
w którym B jest wartością energii mechanicznej wyrażonej w jednostkach wysokości słupa cieczy, z jest wzniesieniem środka ciężkości przekroju poprzecznego strumienia ponad przyjętym poziomem porównawczym, p jest ciśnieniem, v - średnią prędkością strumienia, a jest współczynnikiem de Saint Venanta.
W trakcie przepływu cieczy możliwe są wzajemne przemiany form energii mechanicznej, co określane jest stratami energii mechanicznej, które można rozróżniać jako straty na długości oraz straty lokalne.
Straty na długości obliczamy ze wzoru
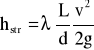
w którym v jest średnią prędkością przepływu strumienia, g - przyspieszeniem ziemskim, zaś jest współczynnikiem oporów liniowych. Współczynnik oporów liniowych odczytujemy z wykresu Moody'ego znając wartość liczby Reynoldsa dla danego ruchu oraz chropowatość względną, która jest stosunkiem chropowatości bezwzględnej oraz średnicy przekroju.
Starty lokalne obliczamy ze wzoru
![]()
w którym ζ jest współczynnikiem oporów lokalnych, g - przyspieszeniem ziemskim, zaś v przyjmuje się jako prędkość za przeszkodą. Wartości współczynników można również odczytywać z tabel.
3. Opis poszczególnych części doświadczenia
b. Część II - Opory ruchu w rurociągach
Opory liniowe
Woda przepływa przez poszczególne części rurociągu pokonując opory liniowe zależne od prędkości, rodzaju ruchu, długości przewodu i średnicy oraz chropowatości wewnętrznej. Piezometry zamontowane na początkach oraz końcach danych odległości wskazują różnicę energii mechanicznej cieczy.
Opory lokalne
Woda przez poszczególne elementy rurociągu traktowane jako przeszkody, takie jak zmiany średnic, załamania przewodu, śrubunki itp.
Pomiary zostały przeprowadzone dla piezometrów 0-35:
1. Ustalenie żądanego przepływu wody poprzez poprzez zawór regulacyjny.
2. Określenie objętości cieczy przepływające przez 5 minut. Dwukrotny pomiar.
3. Jednocześnie z punktem 2 określenie położenia zwierciadeł wody w kolejnych piezometrach. Dwukrotny pomiar.
4. Równocześnie z punktem 2 i 3 pomiar temperatury cieczy.
Cykl od 1 do 4 został wykonany dla dwóch rodzajów natężeń.
5. Część II - Opory ruchu w rurociągach
Schemat stanowiska
W skład stanowiska pomiarowego wchodzą:
• zbiornik górny wraz z przewodami zasilającymi rurociąg i przelewem umożliwiającym
utrzymanie stałego poziomu wody w zbiorniku,
• rurociąg pomiarowy, złożony z odcinków przewodów wykonanych z różnych materiałów (stal
ocynkowana, miedź, polipropylen), połączonych szeregiem różnorodnych kształtek (kolanek,
zmian średnic rury, złączek), umieszczony na poziomym stole pomiarowym,
• zestaw 36 piezometrów, ponumerowanych od 0 do 35, podłączonych w charakterystycznych
punktach przewodu i umieszczonych na zbiorczej tablicy ułatwiającej odczyt (piezometr nr 0
wskazuje położenie zwierciadła wody w zbiorniku górnym i służy jako piezometr porównawczy),
• wodomierz, umożliwiający pomiar objętości przepływającej cieczy,
• zawór regulacyjny, pozwalający na regulację natężenia przepływu przez rurociąg,
• zbiornik dolny, do którego odprowadzana jest woda wypływająca z rurociągu,
• pompa, wraz z przewodem ssawnym i tłocznym, łączącymi zbiornik dolny i zbiornik górny,
umożliwiająca pracę systemu w układzie zamkniętym.
b. Tabele z wynikami pomiarów i obliczeń
Nr pomiaru |
Pomiar wydatku |
Obniżenie zwierciadła wody w piezometrach [cm] |
|||||||||||||||||||||
|
V |
t |
Q |
Qsr |
Odczyt |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
[dm3] |
[s] |
[dm3/s] |
[dm3/s] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
21 |
313 |
0,067 |
0,0665 |
1 |
44,6 |
48,8 |
50 |
51,2 |
51,5 |
51,6 |
53,4 |
55,7 |
58,2 |
60,8 |
61,4 |
61,8 |
63,5 |
63,9 |
64,2 |
64,1 |
64,3 |
64,7 |
|
20 |
304 |
0,066 |
|
2 |
44,6 |
46,6 |
46,7 |
47,3 |
47,4 |
47,6 |
48,4 |
49,9 |
50,9 |
52 |
52,3 |
52,5 |
53,4 |
53,5 |
53,8 |
53,5 |
53,8 |
54 |
|
|
|
|
|
średnio |
44,6 |
47,7 |
48,35 |
49,25 |
49,45 |
49,6 |
50,9 |
52,8 |
54,55 |
56,4 |
56,85 |
57,15 |
58,45 |
58,7 |
59 |
58,8 |
59,05 |
59,35 |
2 |
32 |
310 |
0,103 |
0,1105 |
1 |
44,6 |
54,6 |
57,2 |
60 |
60,5 |
60,7 |
65,3 |
71,1 |
77 |
82,8 |
84,2 |
85,1 |
88,8 |
90 |
90,9 |
90,8 |
90,9 |
91,8 |
|
36 |
306 |
0,118 |
|
2 |
44,6 |
55,1 |
57,8 |
60,8 |
61,3 |
61,3 |
66 |
72,1 |
78,1 |
84,3 |
85,7 |
86,6 |
90,8 |
91,7 |
92,8 |
92,6 |
92,8 |
93,6 |
|
|
|
|
|
średnio |
44,6 |
54,85 |
57,5 |
60,4 |
60,9 |
61 |
65,65 |
71,6 |
77,55 |
83,55 |
84,95 |
85,85 |
89,8 |
90,85 |
91,85 |
91,7 |
91,85 |
92,7 |
Obniżenie zwierciadła wody w piezometrach [cm] |
|||||||||||||||||
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
65,5 |
67,3 |
85,3 |
87,3 |
89,5 |
104,7 |
110,7 |
110,8 |
111,5 |
111,4 |
111,4 |
112,7 |
113,7 |
115,9 |
116 |
117,1 |
119,2 |
54,1 |
54,3 |
55 |
62,7 |
63,9 |
64,8 |
72,2 |
75 |
75,1 |
75,6 |
75,7 |
75,7 |
76 |
76,4 |
77,6 |
77,7 |
78,2 |
79,2 |
59,55 |
59,9 |
61,15 |
74 |
75,6 |
77,15 |
88,45 |
92,85 |
92,95 |
93,55 |
93,55 |
93,55 |
94,35 |
95,05 |
96,75 |
96,85 |
97,65 |
99,2 |
92,7 |
93,5 |
97,6 |
142,2 |
147,5 |
152,4 |
189 |
201,7 |
202 |
203,7 |
203,7 |
203,9 |
206,2 |
208,6 |
213,5 |
213,6 |
216 |
220 |
94,5 |
95,5 |
99,5 |
148,3 |
152,2 |
157 |
194,8 |
208,2 |
208,4 |
210 |
210 |
210 |
212,9 |
215,1 |
221 |
221 |
223,1 |
228 |
93,6 |
94,5 |
98,55 |
145,25 |
149,85 |
154,7 |
191,9 |
204,95 |
205,2 |
206,85 |
206,85 |
206,95 |
209,55 |
211,85 |
217,25 |
217,3 |
219,55 |
224 |
Współczynniki chropowatości bezwzględnej:
-Rura miedziana: k=0.0015
-Rura z polipropylenu: k=0.007
-Rura ocynkowana: k=0.07
Wartości teoretyczne współczynników oporu
Wartości teoretyczne współczynników oporów miejscowych, zostały odczytane z tabeli Współczynników oporów lokalnych, dla zmiany średnic rur, współczynnik został dobrany odpowiednio do stosunku kwadratów średnic przekrojów, dla śrubunku wartość teoretyczna jest równa ξ=0,4, dla podwójnego kolanka ξ=1,98,.
Wartości teoretyczne współczynników strat na długości, zostały dobrane z wykresu Colebrooka i White, przy wykorzystaniu chropowatości względnej przewodów i wartości liczby Reynoldsa obliczonej dla danego przypadku, np. na odcinku między piezometrami 4 i 5 występuje ruch laminarny i wartość teoretycznego współczynnika oporów lokalnych wyznaczamy z zależności λ=64/Re=64/1877,39=0,0341, zaś na odcinku między piezometrami 2 i 3 liczba Reynoldsa odpowiada już strefie przejściowej: Re=5131,54, chropowatość względna k/d wynosi 0,004, więc wartość odczytujemy z wykresu czyli dla tych parametrów λ=0,04.
Pomiar 1
Q [dm^3/s] |
0,0665 |
T ['C] |
17 |
α [-] |
1 |
|
ν |
0,011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nr piezometru i |
di |
vi |
Rei |
(α*vi^2)/2g |
Δh |
hstr |
ξ |
λ |
L |
ξteor |
λteor |
|
|
|
|
|
|
|
|
|
|
|
|
|
[cm] |
[cm/s] |
[-] |
[cm] |
[cm] |
[cm] |
[-] |
[-] |
[cm] |
[-] |
[-] |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
1 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
0,65 |
0,1161 |
0,1609 |
|
|
0,24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1,5 |
37,6313 |
5131,5412 |
0,7218 |
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,9 |
|
0,0425 |
44 |
|
0,04 |
3 |
1,5 |
37,6313 |
5131,5412 |
0,7218 |
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
0,9088 |
70,2843 |
|
|
41,88 |
|
4 |
4,1 |
5,0369 |
1877,3931 |
0,0129 |
|
|
|
|
|
|
|
|
|
|
|
|
0,15 |
0,15 |
|
0,3472 |
137 |
|
0,0341 |
5 |
4,1 |
5,0369 |
1877,3931 |
0,0129 |
|
|
|
|
|
|
|
|
|
|
|
|
1,3 |
0,5912 |
0,8190 |
|
|
0,35 |
|
6 |
1,5 |
37,6313 |
5131,5412 |
0,7218 |
|
|
|
|
|
|
|
|
|
|
|
|
1,9 |
1,9 |
|
0,0627 |
63 |
|
0,04 |
7 |
1,5 |
37,6313 |
5131,5412 |
0,7218 |
|
|
|
|
|
|
|
|
|
|
|
|
1,75 |
2,2839 |
12,1559 |
|
|
2,96 |
|
8 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
|
|
|
|
|
|
|
|
|
|
|
|
1,85 |
1,85 |
|
0,0715 |
289 |
|
0,046 |
9 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
|
|
|
|
|
|
|
|
|
|
|
|
0,45 |
0,45 |
2,3951 |
|
|
1,98 |
|
10 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
0,2595 |
1,1363 |
|
|
0,4 |
|
11 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
1,3 |
1,3 |
|
0,0417 |
273 |
|
0,042 |
12 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
0,25 |
0,25 |
1,0947 |
|
|
1,98 |
|
13 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
0,3 |
|
0,0424 |
62 |
|
0,042 |
14 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
0,3935 |
11,2930 |
|
|
2,25 |
|
15 |
3,2 |
8,2686 |
2405,4099 |
0,0348 |
|
|
|
|
|
|
|
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
15 |
3,2 |
8,2686 |
2405,4099 |
0,0348 |
0,25 |
0,25 |
|
0,1739 |
132 |
|
0,026 |
16 |
3,2 |
8,2686 |
2405,4099 |
0,0348 |
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
0,1065 |
0,4662 |
|
|
0,3 |
|
17 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
0,2 |
|
0,0297 |
59 |
|
0,042 |
18 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
0,35 |
0,35 |
1,5326 |
|
|
1,98 |
|
19 |
2 |
21,1676 |
3848,6559 |
0,2284 |
|
|
|
|
|
|
|
|
|
|
|
|
1,25 |
0,1990 |
0,1556 |
|
|
0,3 |
|
20 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
12,85 |
12,85 |
|
0,0465 |
281 |
|
0,036 |
21 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
1,6 |
1,6 |
1,2506 |
|
|
1,98 |
|
22 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
1,55 |
1,55 |
1,2115 |
|
|
0,4 |
|
23 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
11,3 |
11,3 |
|
0,0416 |
276 |
|
0,036 |
24 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
4,4 |
4,4 |
3,4392 |
|
|
1,98 |
|
25 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,8864 |
1,7980 |
|
|
0,36 |
|
26 |
1,65 |
31,1002 |
4665,0375 |
0,4930 |
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
0,6 |
|
0,0515 |
39 |
|
0,038 |
27 |
1,65 |
31,1002 |
4665,0375 |
0,4930 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,4823 |
45,1252 |
|
|
33,54 |
|
28 |
4,3 |
4,5793 |
1790,0725 |
0,0107 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
140 |
|
0,0358 |
29 |
4,3 |
4,5793 |
1790,0725 |
0,0107 |
|
|
|
|
|
|
|
|
|
|
|
|
0,8 |
0,3177 |
0,6445 |
|
|
0,3 |
|
30 |
1,65 |
31,1002 |
4665,0375 |
0,4930 |
|
|
|
|
|
|
|
|
|
|
|
|
0,7 |
0,7 |
|
0,0397 |
59 |
|
0,038 |
31 |
1,65 |
31,1002 |
4665,0375 |
0,4930 |
|
|
|
|
|
|
|
|
|
|
|
|
1,7 |
1,7 |
3,4484 |
|
|
1,98 |
|
32 |
1,65 |
31,1002 |
4665,0375 |
0,4930 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,4051 |
2,1561 |
|
|
0,36 |
|
33 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
|
|
|
|
|
|
|
|
|
|
|
|
0,8 |
0,8 |
|
0,0361 |
248 |
|
0,042 |
34 |
2,1 |
19,1996 |
3665,3866 |
0,1879 |
|
|
|
|
|
|
|
|
|
|
|
|
1,55 |
0,4585 |
0,3584 |
|
|
0,3 |
|
35 |
1,3 |
50,1008 |
5921,0091 |
1,2794 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pomiar 2
Q [dm^3/s] |
0,1105 |
T ['C] |
17 |
α [-] |
|
v |
0,011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nr piezometru i |
di |
vi |
Rei |
(α*vi^2)/2g |
Δh |
hstr |
ξ |
λ |
L |
ξteor |
λteor |
|
|
|
|
|
|
|
|
|
|
|
|
|
[cm] |
[cm/s] |
[-] |
[cm] |
[cm] |
[cm] |
[-] |
[-] |
[cm] |
[-] |
[-] |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
1 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
2,65 |
1,175884 |
0,5900 |
|
|
0,24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1,5 |
62,5302088 |
8526,8466 |
1,992878 |
|
|
|
|
|
|
|
|
|
|
|
|
2,9 |
2,9 |
|
0,0496 |
44 |
|
0,037 |
3 |
1,5 |
62,5302088 |
8526,8466 |
1,992878 |
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
2,457175 |
68,8217 |
|
|
41,88 |
|
4 |
4,1 |
8,36959962 |
3119,5780 |
0,035703 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,1 |
|
0,0838 |
137 |
|
0,046 |
5 |
4,1 |
8,36959962 |
3119,5780 |
0,035703 |
|
|
|
|
|
|
|
|
|
|
|
|
4,65 |
2,692825 |
1,3512 |
|
|
0,35 |
|
6 |
1,5 |
62,5302088 |
8526,8466 |
1,992878 |
|
|
|
|
|
|
|
|
|
|
|
|
5,95 |
5,95 |
|
0,0711 |
63 |
|
0,037 |
7 |
1,5 |
62,5302088 |
8526,8466 |
1,992878 |
|
|
|
|
|
|
|
|
|
|
|
|
5,95 |
7,424116 |
14,3112 |
|
|
2,96 |
|
8 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
0,0840 |
289 |
|
0,038 |
9 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
|
|
|
|
|
|
|
|
|
|
|
|
1,4 |
1,4 |
2,6987 |
|
|
1,98 |
|
10 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,788203 |
1,2500 |
|
|
0,4 |
|
11 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
3,95 |
3,95 |
|
0,0459 |
273 |
|
0,034 |
12 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
1,05 |
1,05 |
1,6652 |
|
|
1,98 |
|
13 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
0,0512 |
62 |
|
0,034 |
14 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
0,15 |
0,684343 |
7,1126 |
|
|
2,25 |
|
15 |
3,2 |
13,7395478 |
3996,9594 |
0,096216 |
|
|
|
|
|
|
|
|
|
|
|
|
0,15 |
0,15 |
|
0,0378 |
132 |
|
0,042 |
16 |
3,2 |
13,7395478 |
3996,9594 |
0,096216 |
|
|
|
|
|
|
|
|
|
|
|
|
0,85 |
0,315657 |
0,5006 |
|
|
0,3 |
|
17 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,9 |
|
0,0484 |
59 |
|
0,034 |
18 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,9 |
1,4273 |
|
|
1,98 |
|
19 |
2 |
35,1732424 |
6395,1350 |
0,630559 |
|
|
|
|
|
|
|
|
|
|
|
|
4,05 |
1,148139 |
0,3250 |
|
|
0,3 |
|
20 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
46,7 |
46,7 |
|
0,0612 |
281 |
|
0,032 |
21 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
4,6 |
4,6 |
1,3022 |
|
|
1,98 |
|
22 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
22 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
4,85 |
4,85 |
1,3730 |
|
|
0,4 |
|
23 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
37,2 |
37,2 |
|
0,0496 |
276 |
|
0,029 |
24 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
13,05 |
13,05 |
3,6944 |
|
|
1,98 |
|
25 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
0,25 |
2,421258 |
1,7788 |
|
|
0,36 |
|
26 |
1,65 |
51,6778585 |
7751,6788 |
1,361163 |
|
|
|
|
|
|
|
|
|
|
|
|
1,65 |
1,65 |
|
0,0513 |
39 |
|
0,033 |
27 |
1,65 |
51,6778585 |
7751,6788 |
1,361163 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1,331652 |
45,1252 |
|
|
33,54 |
|
28 |
4,3 |
7,60913844 |
2974,4814 |
0,02951 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,1 |
|
0,1041 |
140 |
|
0,023 |
29 |
4,3 |
7,60913844 |
2974,4814 |
0,02951 |
|
|
|
|
|
|
|
|
|
|
|
|
2,6 |
1,268348 |
0,9318 |
|
|
0,3 |
|
30 |
1,65 |
51,6778585 |
7751,6788 |
1,361163 |
|
|
|
|
|
|
|
|
|
|
|
|
2,3 |
2,3 |
|
0,0473 |
59 |
|
0,034 |
31 |
1,65 |
51,6778585 |
7751,6788 |
1,361163 |
|
|
|
|
|
|
|
|
|
|
|
|
5,4 |
5,4 |
3,9672 |
|
|
1,98 |
|
32 |
1,65 |
51,6778585 |
7751,6788 |
1,361163 |
|
|
|
|
|
|
|
|
|
|
|
|
0,05 |
0,8924 |
1,7202 |
|
|
0,36 |
|
33 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
|
|
|
|
|
|
|
|
|
|
|
|
2,25 |
2,25 |
|
0,0367 |
248 |
|
0,036 |
34 |
2,1 |
31,9031677 |
6090,6047 |
0,518763 |
|
|
|
|
|
|
|
|
|
|
|
|
4,45 |
1,436342 |
0,4066 |
|
|
0,3 |
|
35 |
1,3 |
83,2502779 |
9838,6692 |
3,53242 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Przykłady obliczeń z przeliczeniem jednostek:
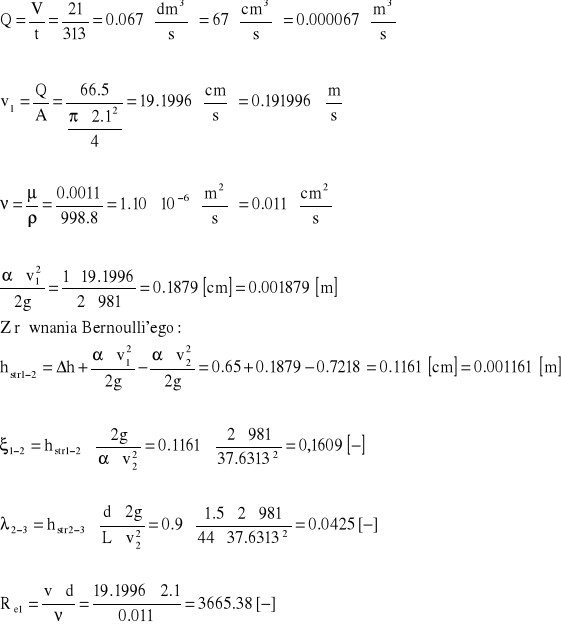
Rysunek układu linii ciśnienia i linii energii pomiędzy dwoma wybranymi piezometrami
Piezometry 20-21 (Pomiar 1)
Piezometry 20-21 (Pomiar 2)
Wnioski
Część wartości doświadczalnych i teoretycznych λ, pokrywa się ze sobą, a część różni się od siebie, ale pokazują podobne zmiany. Przyczyną jest fakt, iż rodzaj ruchu wody znajduje się w strefie przejściowej liczby Reynoldsa. Może być to również spowodowane inną chropowatością przewodów niż wynika to z teorii. Wartości doświadczalne współczynników strat lokalnych ξ są bardziej zbliżone do wartości teoretycznej gdy liczba Reynoldsa wzrasta, czyli zwiększa się szansa powstania ruchu turbulentnego. Wartości oporów miejscowych różnią się znacznie w miejscach śrubunków, wynika to
z tego gdyż teoretyczne współczynniki nie uwzględniają zmian materiałów.
Najwięcej strat energii otrzymuje się na liniowych odcinkach, im bardziej turbulentny jest ruch wody tym powstają większe straty. Zmiana przekroju z mniejszego na większy powoduje większe straty niż odwrotna zmiana przekroju. Większy spadek energii można zauważyć podczas zmiany rury miedzianej na polipropylenową niż podczas zmiany z rury stalowej ocynkowanej na miedzianą. Na kolankach występują stosunkowo małe straty energii.
Posługiwanie się tablicami do wyznaczania współczynników oporu λ i ξ jest obarczone błędem szczególnie wtedy gdy trudno jest określić chropowatość rury czy występuje zmiana materiału przewodu. Różnica między wartościami teoretycznymi oraz doświadczalnymi może również wynikać
z innych nieprzewidzianych błędów pomiarowych.
Wyszukiwarka