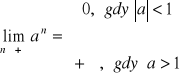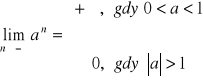4. GRANICA CIĄGU. GRANICA FUNKCJI.
Zad 4.1.
Funkcję
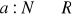
nazywamy ciągiem liczbowym, a jej wartości a(1), a(2),..., a(n),.... wyrazami ciągu. Ciąg oznaczamy symbolicznie {an}.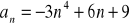
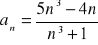
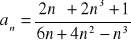
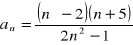
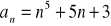
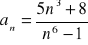
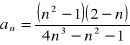
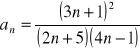
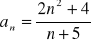
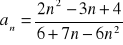
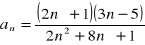
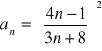
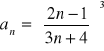
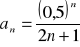
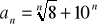
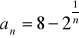
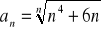
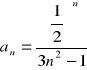
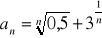
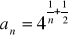
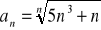
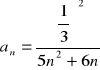
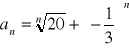
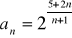
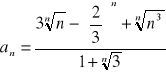
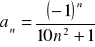
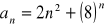
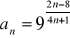
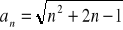
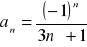
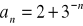
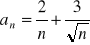
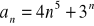
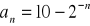
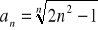
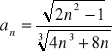
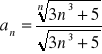
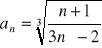
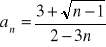
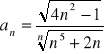
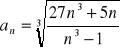
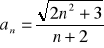
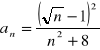
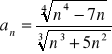
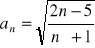
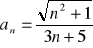
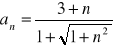
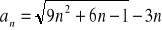
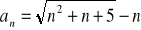
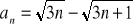
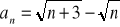
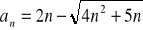
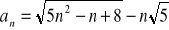
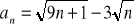
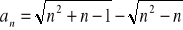
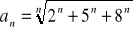
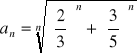
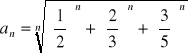
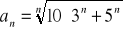
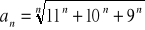
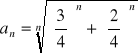
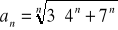
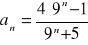
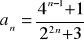
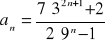
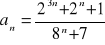
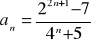
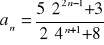
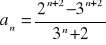
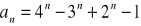

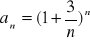
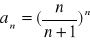
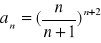
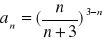
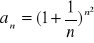
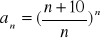
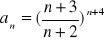
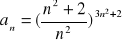
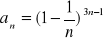
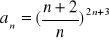
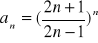
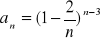
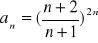
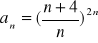
Liczbę g nazywamy granicą funkcji w punkcie
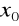
, co zapisujemy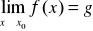
, jeżeli istnieją granice lewostronna i prawostronna w punkcie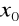
i obie są równe liczbie g, tzn. jeżeli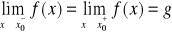
.Gdy
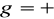
lub gdy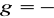
, mówimy, że funkcja f w punkcie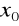
ma granicę niewłaściwą.Gdy
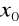
należy do dziedziny funkcji, do wzoru funkcji w miejsce x podstawiamy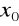
i wyliczamy wartość funkcji.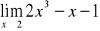
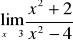
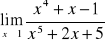
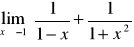
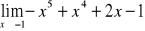
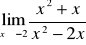
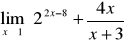
Gdy
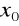
nie należy do dziedziny funkcji - jeśli jest to możliwe, to przekształcamy tak ułamek, aby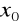
należał do dziedziny wyrażenia przekształconego, a następnie do wzoru funkcji w miejsce x podstawiamy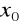
i wyliczamy wartość funkcji.Przydatne wzory:
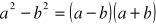
,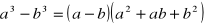
,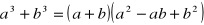
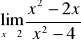
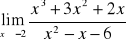
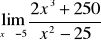
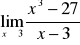
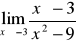
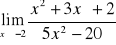
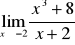
Gdy
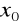
nie należy do dziedziny funkcji i nie jest możliwe takie przekształcenie ułamka, aby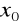
należał do dziedziny wyrażenia przekształconego, otrzymujemy granicę niewłaściwą funkcji f w punkcie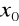
tzn.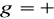
lub gdy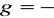
.Należy wtedy sprawdzić, czy granica lewostronna równa się granicy prawostronnej
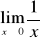
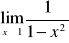
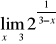
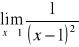
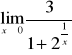
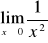
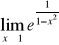
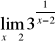
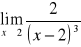
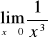
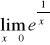
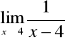
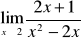
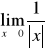
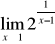
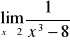
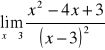
W przypadku gdy we wzorze funkcji znajduje się wielomian, zawsze wyłączamy przed nawias zmienną w najwyższej potędze
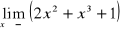
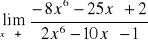
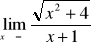
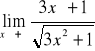
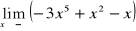
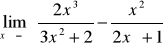
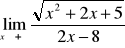
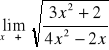
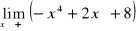
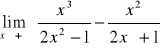
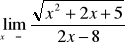
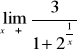

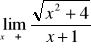
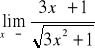
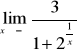
Przydatne wzory:
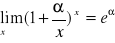
,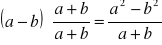
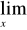
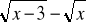
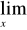
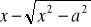
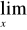
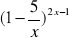
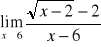
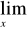
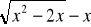
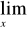
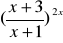
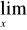
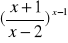
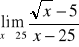
Przydatne wzory
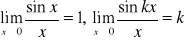
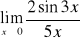
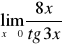
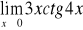

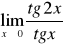
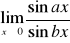
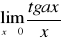
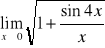
0
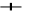
0
1
0
2
2
1
0
1
4
2
0
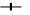
3
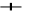
0
2
0
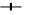
10
1
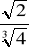
0
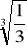
0
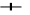
3
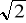
0
1
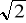
1/3
1
1
1/2
0
0
-5/4
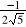
0
1
8
2/3
2/3
5
11
3/4
7
4
1/4
21/2
1
2
5/16
-9
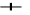
P
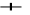
,L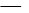
P
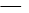
,L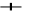
P 0,L
P
,L
P 0, L 3
P
,L
P 0,L
P
,L 0P
,L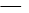
P
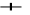
,L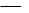
P
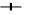
,L 0P
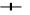
,L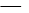
P
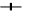
,L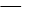
P
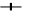
,L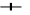
P
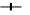
,L 0P
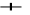
,L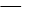
P
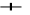
,L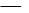
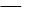
-4
-1
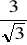
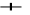
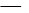
1/2
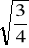
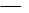
1/4
-1/2
3/2
3/2
1
-
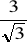
3/2
6/5
8/3
3/4

2a/b
a
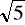
0
0
e-10
1/4
-1
e4
e3
1/10
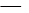
5
-2
1/2
0
-1/4
9/8
-1/3
3
16/9
8/27

e31/e
1/e

e3
e2
e10e

e6
e-3
e4e

e-2
e2
e813
11/5
1/8
1
-1
2/8
65/64
2/4
2/5
-15
27
1/6
1/20
16
Jeśli a>0 |
Jeśli a<0 |
a( |
a( |
a( |
a( |
|
|
|
|
|
|
Oblicz granicę ciągu o wyrazie ogólnym:
Zad 4.2
|
|
|
|
||
|
|
Symbole nieoznaczone |
|||
Oblicz granicę ciągu o wyrazie ogólnym:
Zad 4.3
Oblicz granicę ciągu o wyrazie ogólnym:
Zad 4.4![]()
Oblicz granicę ciągu o wyrazie ogólnym:
Zad 4.5
Tw. O trzech ciągach
Jeżeli ![]()
![]()
oraz ciągi skrajne są zbieżne ![]()
to ciąg ![]()
.
Oblicz granicę ciągu o wyrazie ogólnym:
Zad 4.6
Zad 4.7
Oblicz granicę ciągu o wyrazie ogólnym, wykorzystując następujący wzór:
![]()
, ![]()
Zad 4.8
Oblicz granicę funkcji w punkcie
Zad 4.9
Liczbę g nazywamy granicą funkcji f przy ![]()
, jeżeli dla każdego ciągu argumentów ![]()
rozbieżnego do![]()
odpowiadający mu ciąg wartości funkcji (f![]()
) jest zawsze ciągiem zbieżnym do g, co zapisujemy: ![]()
. Podobnie definiujemy granicę funkcji, gdy ![]()
.
Oblicz granicę funkcji w nieskończoności.
Zad 4.10
Oblicz granicę funkcji w nieskończoności.
Zad 4.11
Oblicz granicę funkcji w punkcie
|
Zad 4.1. Zad 4.2
Zad 4.4
Zad 4.3
Zad 4.6
Zad 4.5
Zad 4.7 Zad 4.8
Zad 4.8
Zad 4.9
Zad 4.11
Zad 4.10 |
|||
Opracowała: K. Sokołowska 5
Wyszukiwarka