Tomasz Przybył R33
Zespół nr.6
LABORATORIUM FIZYKI II
Ćwiczenie nr. 1
Temat: Licznik G-M. Badanie statystycznego charakteru przemiany promieniotwórczej.
Cel ćwiczenia
Celem pierwszej części ćwiczenia było zapoznanie się z budową i zasadą działania licznika Geigera-Mullera. W części pomiarowej dokonano pomiarów napięcia licznika i opowiadającej mu szybkości zliczania impulsów w celu wyznaczenia charakterystyki roboczej licznika. Wykonano również pomiary szybkości zliczania impulsów dla dwóch próbek promieniotwórczych razem oraz dla każdej z osobna. Posłużyło to następnie do obliczenia czasu martwego licznika.
Druga część ćwiczenia poświęcona była poznaniu statystycznych praw opisujących rozpad promieniotwórczy. Na podstawie uzyskanych rozkładów doświadczalnych przeprowadzona została analiza statystycznego charakteru promieniowania.
Charakterystyka robocza licznika Geigera-Mullera
W doświadczeniu zmierzona została zależność N (liczba impulsów w czasie 10s) w funkcji napięcia licznika U [V]. Na podstawie tych pomiarów można wyznaczyć charakterystykę roboczą licznika I = f(U).
Tabela 1 - Charakterystyka licznika
U [v] |
495 |
496 |
498 |
500 |
504 |
506 |
508 |
514 |
520 |
530 |
540 |
550 |
560 |
570 |
N [imp/10s] |
70 |
920 |
1984 |
2044 |
2138 |
2264 |
2270 |
2380 |
2436 |
2493 |
2460 |
2480 |
2517 |
2564 |
I [imp/min] |
420 |
5520 |
11904 |
12264 |
12828 |
13584 |
13620 |
14280 |
14616 |
14958 |
14760 |
14880 |
15102 |
15384 |
σ = √I/t |
2,646 |
9,592 |
14,09 |
14,3 |
14,62 |
15,05 |
15,07 |
15,43 |
15,61 |
15,79 |
15,68 |
15,75 |
15,87 |
16,01 |
580 |
590 |
600 |
610 |
620 |
630 |
640 |
650 |
660 |
670 |
680 |
690 |
700 |
710 |
720 |
2564 |
2516 |
2608 |
2612 |
2625 |
2689 |
2776 |
2890 |
3050 |
3321 |
3702 |
4217 |
4962 |
6162 |
6770 |
15384 |
15096 |
15648 |
15672 |
15750 |
16134 |
16656 |
17340 |
18300 |
19926 |
22212 |
25302 |
29772 |
36972 |
40620 |
16,01 |
15,86 |
16,15 |
16,16 |
16,2 |
16,4 |
16,66 |
17 |
17,46 |
18,22 |
19,24 |
20,54 |
22,28 |
24,82 |
26,02 |
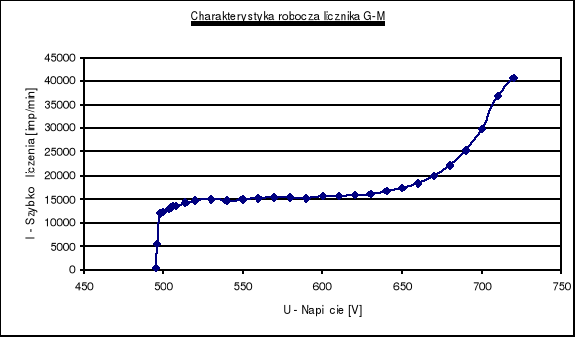
Napięcie progowe: Ugr = 495 [V]
Obszar plateau zawarty pomiędzy wartościami:
U1 = 514 [V]
U2 = 640 [V]
Napięcie pracy: Up = (U1 + U2)/2 = 577 [V]
Długość obszaru plateau: ΔU = U2 - U1 = 126 [V]
Nachylenie plateau: 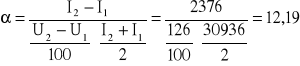
[%/100V]
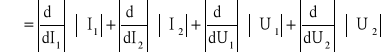
Analiza błędów:
ΔIx = (dI / dN ) × ΔNx , gdzie ΔNx = 3 * ![]()
(zgodnie z rozkładem Poissona σ = ![]()
)
ΔI1 = 146 [imp/min]
ΔI2 = 158 [imp/min]
ΔU1 = ΔU2 = 2 [V] (wartość działki elementarnej)
![]()
![]()
-0,000967545
![]()
-0,000055250
![]()
0,000047368
zatem Δα = 1,942 ≈ 2 [%/100V]
Ostatecznie nachylenie plateau wynosi α = 12 ± 2 [%/100V]
Wyznaczona charakterystyka robocza licznika ma kształt, który był oczekiwany. Fragment szybkiego wzrostu I (szybkości zliczania impulsów) po przekroczeniu napięcia progowego jest bardzo stromy. Obszar `plateau' charakteryzuje się pochyleniem rzędu 12 [%/100V], co świadczy o niezbyt wysokiej klasie badanego licznika. Potwierdza to również długość obszaru `plateau', która nie jest zbyt duża (126 [V]). Na końcu obszaru `plateau' charakterystyka rośnie parabolicznie względnie łagodnie, co spowodowane jest wzrostem prawdopodobieństwa wyładowania samoistnego. Wyładowanie takie powoduje zliczenie `fałszywego' impulsu, który nie jest wywołany przez cząstkę wyemitowaną z badanej próbki promieniotwórczej. Napięcie progowe Ug = 495 [V], podobnie jak i napięcie pracy Up = 577 [V], są wysokie, co może sugerować, że badany licznik nie jest licznikiem o obniżonym napięciu pracy.
Czas martwy licznika Geigera-Mullera
Druga część ćwiczenia miała na celu określenie czasu martwego badanego licznika, który jest głównym czynnikiem ograniczającym szybkość zliczania impulsów. Wyznaczenie to opierało się na pomiarze aktywności dwóch próbek osobno i obydwu razem. Uzyskane wyniki znajdują się w poniższej tabeli:
Tabela 2 - Zestawienie dotyczące czasu martwego (Itła = 17,7 [imp/min])
Nr preparatu |
t [min] |
N [imp] |
In [imp/min] |
I = In - Itła |
1 |
10 |
152542 |
15254,2 |
15242,5 |
1+2 |
10 |
256336 |
25633,6 |
25621,9 |
2 |
10 |
116196 |
11619,6 |
11607,9 |
Wyniki pomiarów aktywności za pomocą licznika Geigera-Mullera stwierdzają brak zgodności w przypadku aktywności zmierzonych próbek (obydwu razem i osobno). Wynika ona z tego, że pomiar aktywności obarczony jest błędem wynikającym z istnienia czasu martwego. Czas martwy powoduje nie zliczenie większej ilości cząstek, powodujących wzbudzenie licznika niż przy pomiarze mniejszych aktywności. Cząstki są częściej wysyłane i częściej trafiają na licznik w stanie martwym. Dlatego zmierzona aktywność połączonych próbek jest mniejsza niż suma zmierzonych aktywności obu próbek z osobna.
Znając zależność między intensywnością rzeczywistą a intensywnością zmierzoną, można obliczyć czas martwy z następującej zależności:
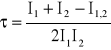
= 3,472 [μs]
gdzie:
τ - to czas martwy licznika;
I1 - to zmierzona intensywność pierwszej próbki;
I2 - to zmierzona intensywność drugiej próbki;
I1,2 - to zmierzona intensywność obu próbek razem;
Analiza błędów:
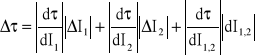
ΔIx = (dI / dN ) × ΔNx + (dI / dt) × Δt, gdzie ΔNx = 3 * ![]()
(zgodnie z rozkładem Poissona σ = ![]()
; natomiast błąd związany z pomiarem czasu Δt można pominąć)
zatem:
ΔI1 = 117 [imp/min]
ΔI1,2 = 102 [imp/min]
ΔI2 = 152 [imp/min]
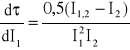
= 0,000000002598
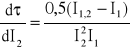
= 0,000000002527
![]()
= 0,000000002826
zatem Δτ = 0,339 ≈ 0,4 [μs]
Ostatecznie czas martwy licznika wynosi: τ = 3,4 ± 0,4 [μs]
Różnica między sumą aktywności dwóch próbek osobno i aktywnością tych próbek razem osiąga ok. 7 %. Świadczy to o konieczności uwzględniania czasu martwego przy pomiarach próbek o dużej aktywności. Uzyskana wartość τ = 53,4 [μs] jest względnie duża, jednak jej zmniejszanie w większości przypadków zastosowań licznika Geigera-Mullera nie ma sensu. Powodowałoby ono konieczność stosowania urządzeń o wiele droższych, których konstrukcja i gaz wypełniający pozwalają zmniejszyć czas martwy. Jednakże liczniki G-M najczęściej mierzą stopień napromieniowania substancji, więc zmniejszanie τ kosztem wzrostu ceny licznika mija się z celem, bowiem zwiększenie dokładności pomiaru aktywności nie jest tu konieczne. Czas martwy wyznaczony został z dość dużym błędem granicznym, który prawdopodobnie powinien być większy ze względu na źródła błędów, których nie uwzględniono oraz fakt, że zależność wykorzystana do wyznaczenia τ była przybliżona (dane z instrukcji do ćwiczenia). Pominiętych źródeł błędów może być wiele z powodu złożoności procesu emisji jądrowej.
Badanie statystycznego charakteru rozpadu promieniotwórczego
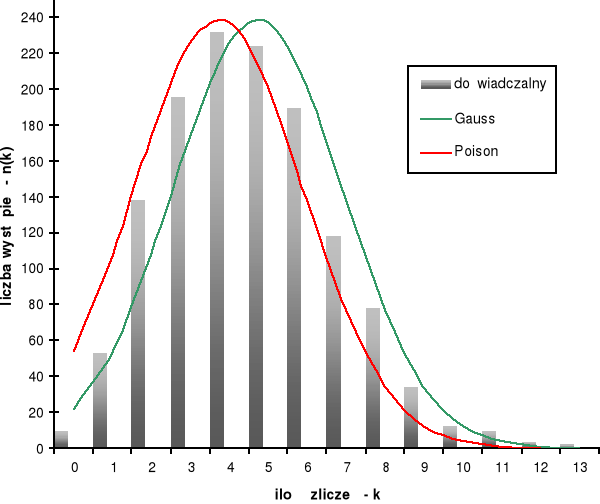
Wyznaczanie własności statystycznych rozpadu promieniotwórczego polegało na rejestrowaniu w przedziale czasu 10 min. impulsów pochodzących z licznika Geigera-Mullera. Wyniki pomiarów zostały zarejestrowane w tabelce i zilustrowane w postaci wykresu. Ilość pomiarów dokonywanych przez komputer w czasie 0,1 s została dobrana poprzez wstępne pomiary z których otrzymaliśmy średnią i odchylenie standardowe, na podstawie których wybrano ilość pomiarów = 3*σ*100.
Seria 1
Rozkład doświadczalny |
Rozkład Poissona |
Rozkład Gaussa |
||||||||||
k |
n(k) |
P(k) |
k*P(k) |
k2*P(k) |
Pp(k) |
np(k) |
χ2(k) |
x |
ρG |
PG |
nG |
χ2(k) |
0 |
10 |
0,77% |
0,00 |
0,0 |
0,88% |
11 |
0,18 |
-2,2 |
3,68% |
1,70% |
22 |
6,58 |
1 |
53 |
4,08% |
0,04 |
0,0 |
4,16% |
54 |
0,02 |
-1,7 |
9,05% |
4,18% |
54 |
0,03 |
2 |
138 |
10,62% |
0,21 |
0,4 |
9,86% |
128 |
0,76 |
-1,3 |
18,01% |
8,31% |
108 |
8,30 |
3 |
196 |
15,08% |
0,45 |
1,4 |
15,55% |
202 |
0,19 |
-0,8 |
28,98% |
13,37% |
174 |
2,83 |
4 |
232 |
17,85% |
0,71 |
2,9 |
18,40% |
239 |
0,22 |
-0,3 |
37,68% |
17,38% |
226 |
0,16 |
5 |
224 |
17,23% |
0,86 |
4,3 |
17,42% |
226 |
0,03 |
0,1 |
39,59% |
18,27% |
237 |
0,77 |
6 |
190 |
14,62% |
0,88 |
5,3 |
13,74% |
179 |
0,73 |
0,6 |
33,63% |
15,52% |
202 |
0,68 |
7 |
118 |
9,08% |
0,64 |
4,4 |
9,29% |
121 |
0,06 |
1,0 |
23,09% |
10,65% |
138 |
3,03 |
8 |
78 |
6,00% |
0,48 |
3,8 |
5,50% |
71 |
0,60 |
1,5 |
12,81% |
5,91% |
77 |
0,02 |
9 |
34 |
2,62% |
0,24 |
2,1 |
2,89% |
38 |
0,34 |
2,0 |
5,74% |
2,65% |
34 |
0,01 |
10 |
12 |
0,92% |
0,09 |
0,9 |
1,37% |
18 |
1,88 |
2,4 |
2,08% |
0,96% |
12 |
0,02 |
11 |
10 |
0,77% |
0,08 |
0,9 |
0,59% |
8 |
0,72 |
2,9 |
0,61% |
0,28% |
4 |
10,99 |
12 |
3 |
0,23% |
0,03 |
0,3 |
0,23% |
3 |
0,00 |
3,4 |
0,14% |
0,07% |
1 |
5,26 |
13 |
2 |
0,15% |
0,02 |
0,3 |
0,08% |
1 |
0,74 |
3,8 |
0,03% |
0,01% |
0 |
20,29 |
r |
Σn(k) |
|
|
|
σ |
|
χp2 |
|
|
|
|
χG2 |
14 |
1300 |
|
4 |
27,10 |
2,17 |
|
6,47 |
|
|
|
|
58,96 |
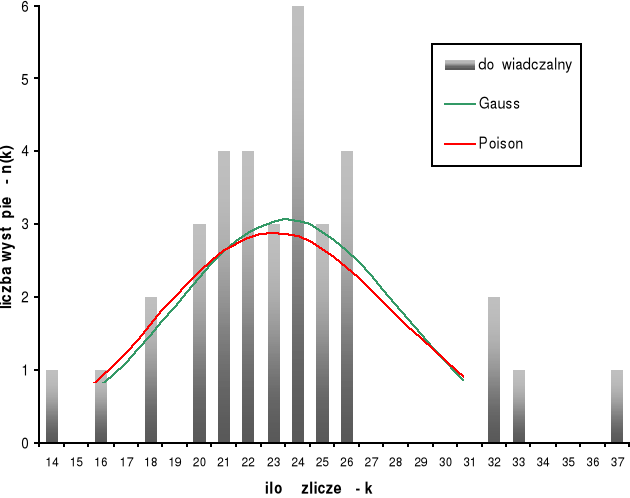
Seria 2
Rozkład doświadczalny |
Rozkład Poissona |
Rozkład Gaussa |
||||||||||
k |
n(k) |
P(k) |
k*P(k) |
k2*P(k) |
Pp(k) |
np(k) |
χ2(k) |
x |
ρG |
PG |
nG |
χ2(k) |
14 |
1 |
2,86% |
0,40 |
5,6 |
1,10% |
0,4 |
0,98 |
-2,1 |
4,48% |
0,98% |
0,3 |
1,25 |
15 |
0 |
0,00% |
0,00 |
0,0 |
1,73% |
0,6 |
0,60 |
-1,9 |
6,91% |
1,52% |
0,5 |
0,53 |
16 |
1 |
2,86% |
0,46 |
7,3 |
2,54% |
0,9 |
0,01 |
-1,7 |
10,17% |
2,23% |
0,8 |
0,06 |
17 |
0 |
0,00% |
0,00 |
0,0 |
3,52% |
1,2 |
1,23 |
-1,4 |
14,27% |
3,13% |
1,1 |
1,09 |
18 |
2 |
5,71% |
1,03 |
18,5 |
4,60% |
1,6 |
0,09 |
-1,2 |
19,08% |
4,18% |
1,5 |
0,20 |
19 |
0 |
0,00% |
0,00 |
0,0 |
5,70% |
2,0 |
1,99 |
-1,0 |
24,30% |
5,33% |
1,9 |
1,86 |
20 |
3 |
8,57% |
1,71 |
34,3 |
6,71% |
2,3 |
0,18 |
-0,8 |
29,51% |
6,47% |
2,3 |
0,24 |
21 |
4 |
11,43% |
2,40 |
50,4 |
7,52% |
2,6 |
0,71 |
-0,6 |
34,16% |
7,49% |
2,6 |
0,73 |
22 |
4 |
11,43% |
2,51 |
55,3 |
8,05% |
2,8 |
0,50 |
-0,3 |
37,68% |
8,26% |
2,9 |
0,43 |
23 |
3 |
8,57% |
1,97 |
45,3 |
8,24% |
2,9 |
0,00 |
-0,1 |
39,61% |
8,68% |
3,0 |
0,00 |
24 |
6 |
17,14% |
4,11 |
98,7 |
8,08% |
2,8 |
3,56 |
0,1 |
39,69% |
8,70% |
3,0 |
2,87 |
25 |
3 |
8,57% |
2,14 |
53,6 |
7,61% |
2,7 |
0,04 |
0,3 |
37,91% |
8,31% |
2,9 |
0,00 |
26 |
4 |
11,43% |
2,97 |
77,3 |
6,89% |
2,4 |
1,05 |
0,5 |
34,51% |
7,56% |
2,6 |
0,69 |
27 |
0 |
0,00% |
0,00 |
0,0 |
6,01% |
2,1 |
2,10 |
0,8 |
29,94% |
6,56% |
2,3 |
2,30 |
28 |
0 |
0,00% |
0,00 |
0,0 |
5,05% |
1,8 |
1,77 |
1,0 |
24,76% |
5,43% |
1,9 |
1,90 |
29 |
0 |
0,00% |
0,00 |
0,0 |
4,10% |
1,4 |
1,44 |
1,2 |
19,51% |
4,28% |
1,5 |
1,50 |
30 |
0 |
0,00% |
0,00 |
0,0 |
3,22% |
1,1 |
1,13 |
1,4 |
14,66% |
3,21% |
1,1 |
1,12 |
31 |
0 |
0,00% |
0,00 |
0,0 |
2,44% |
0,9 |
0,86 |
1,6 |
10,49% |
2,30% |
0,8 |
0,80 |
32 |
2 |
5,71% |
1,83 |
58,5 |
1,80% |
0,6 |
2,99 |
1,9 |
7,16% |
1,57% |
0,5 |
3,83 |
33 |
1 |
2,86% |
0,94 |
31,1 |
1,28% |
0,4 |
0,68 |
2,1 |
4,66% |
1,02% |
0,4 |
1,16 |
34 |
0 |
0,00% |
0,00 |
0,0 |
0,89% |
0,3 |
0,31 |
2,3 |
2,89% |
0,63% |
0,2 |
0,22 |
35 |
0 |
0,00% |
0,00 |
0,0 |
0,60% |
0,2 |
0,21 |
2,5 |
1,71% |
0,37% |
0,1 |
0,13 |
36 |
0 |
0,00% |
0,00 |
0,0 |
0,39% |
0,1 |
0,14 |
2,7 |
0,96% |
0,21% |
0,1 |
0,07 |
37 |
1 |
2,86% |
1,06 |
39,1 |
0,25% |
0,1 |
9,58 |
2,9 |
0,52% |
0,11% |
0,0 |
23,34 |
r |
Σn(k) |
|
|
|
σ |
|
χp2 |
|
|
|
|
χG2 |
24 |
35 |
|
23 |
575,09 |
4,56 |
|
32,15 |
|
|
|
|
46,33 |
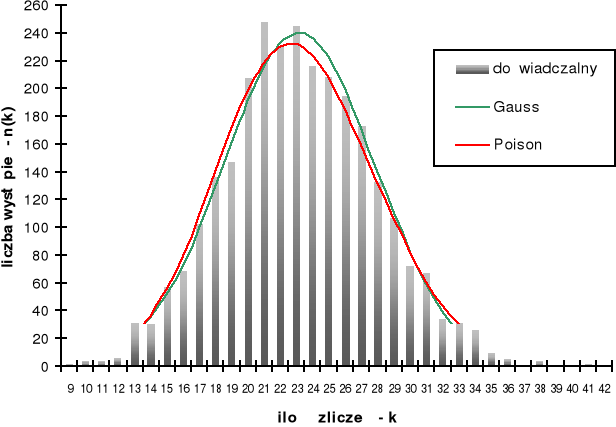
Seria 3
Rozkład doświadczalny |
Rozkład Poissona |
Rozkład Gaussa |
||||||||||
k |
n(k) |
P(k) |
k*P(k) |
k2*P(k) |
Pp(k) |
np(k) |
χ2(k) |
x |
ρG |
PG |
nG |
χ2(k) |
9 |
2 |
0,07% |
0,01 |
0,1 |
0,05% |
1 |
0,42 |
-3,0 |
0,38% |
0,08% |
2 |
0,04 |
10 |
3 |
0,11% |
0,01 |
0,1 |
0,11% |
3 |
0,00 |
-2,8 |
0,72% |
0,15% |
4 |
0,40 |
11 |
3 |
0,11% |
0,01 |
0,1 |
0,22% |
6 |
1,66 |
-2,6 |
1,29% |
0,28% |
8 |
2,92 |
12 |
6 |
0,21% |
0,03 |
0,3 |
0,43% |
12 |
3,01 |
-2,4 |
2,21% |
0,48% |
13 |
4,02 |
13 |
31 |
1,11% |
0,14 |
1,9 |
0,77% |
21 |
4,28 |
-2,2 |
3,63% |
0,78% |
22 |
3,86 |
14 |
30 |
1,07% |
0,15 |
2,1 |
1,27% |
35 |
0,85 |
-2,0 |
5,67% |
1,22% |
34 |
0,50 |
15 |
57 |
2,04% |
0,31 |
4,6 |
1,96% |
55 |
0,08 |
-1,8 |
8,48% |
1,82% |
51 |
0,70 |
16 |
68 |
2,43% |
0,39 |
6,2 |
2,84% |
79 |
1,66 |
-1,5 |
12,09% |
2,60% |
73 |
0,31 |
17 |
103 |
3,68% |
0,63 |
10,6 |
3,87% |
108 |
0,27 |
-1,3 |
16,47% |
3,54% |
99 |
0,15 |
18 |
136 |
4,86% |
0,87 |
15,7 |
4,99% |
140 |
0,10 |
-1,1 |
21,42% |
4,60% |
129 |
0,39 |
19 |
147 |
5,25% |
1,00 |
19,0 |
6,09% |
170 |
3,23 |
-0,9 |
26,60% |
5,72% |
160 |
1,07 |
20 |
208 |
7,43% |
1,49 |
29,7 |
7,06% |
198 |
0,54 |
-0,7 |
31,54% |
6,78% |
190 |
1,73 |
21 |
248 |
8,86% |
1,86 |
39,1 |
7,79% |
218 |
4,06 |
-0,5 |
35,72% |
7,68% |
215 |
5,08 |
22 |
230 |
8,21% |
1,81 |
39,8 |
8,21% |
230 |
0,00 |
-0,3 |
38,61% |
8,30% |
232 |
0,02 |
23 |
245 |
8,75% |
2,01 |
46,3 |
8,28% |
232 |
0,74 |
0,0 |
39,86% |
8,57% |
240 |
0,11 |
24 |
216 |
7,71% |
1,85 |
44,4 |
8,00% |
224 |
0,29 |
0,2 |
39,29% |
8,45% |
236 |
1,77 |
25 |
209 |
7,46% |
1,87 |
46,7 |
7,42% |
208 |
0,01 |
0,4 |
36,98% |
7,95% |
223 |
0,83 |
26 |
194 |
6,93% |
1,80 |
46,8 |
6,62% |
185 |
0,40 |
0,6 |
33,23% |
7,14% |
200 |
0,18 |
27 |
173 |
6,18% |
1,67 |
45,0 |
5,68% |
159 |
1,20 |
0,8 |
28,52% |
6,13% |
172 |
0,01 |
28 |
133 |
4,75% |
1,33 |
37,2 |
4,71% |
132 |
0,01 |
1,0 |
23,37% |
5,02% |
141 |
0,42 |
29 |
107 |
3,82% |
1,11 |
32,1 |
3,76% |
105 |
0,02 |
1,2 |
18,28% |
3,93% |
110 |
0,08 |
30 |
72 |
2,57% |
0,77 |
23,1 |
2,91% |
81 |
1,10 |
1,5 |
13,66% |
2,94% |
82 |
1,27 |
31 |
67 |
2,39% |
0,74 |
23,0 |
2,18% |
61 |
0,60 |
1,7 |
9,74% |
2,09% |
59 |
1,19 |
32 |
34 |
1,21% |
0,39 |
12,4 |
1,58% |
44 |
2,34 |
1,9 |
6,64% |
1,43% |
40 |
0,88 |
33 |
31 |
1,11% |
0,37 |
12,1 |
1,11% |
31 |
0,00 |
2,1 |
4,32% |
0,93% |
26 |
0,97 |
34 |
26 |
0,93% |
0,32 |
10,7 |
0,76% |
21 |
1,11 |
2,3 |
2,68% |
0,58% |
16 |
6,04 |
35 |
9 |
0,32% |
0,11 |
3,9 |
0,50% |
14 |
1,80 |
2,5 |
1,59% |
0,34% |
10 |
0,03 |
36 |
5 |
0,18% |
0,06 |
2,3 |
0,32% |
9 |
1,80 |
2,8 |
0,90% |
0,19% |
5 |
0,03 |
37 |
1 |
0,04% |
0,01 |
0,5 |
0,20% |
6 |
3,84 |
3,0 |
0,49% |
0,10% |
3 |
1,27 |
38 |
3 |
0,11% |
0,04 |
1,5 |
0,12% |
3 |
0,06 |
3,2 |
0,25% |
0,05% |
2 |
1,47 |
39 |
0 |
0,00% |
0,00 |
0,0 |
0,07% |
2 |
2,05 |
3,4 |
0,12% |
0,03% |
1 |
0,74 |
40 |
0 |
0,00% |
0,00 |
0,0 |
0,04% |
1 |
1,19 |
3,6 |
0,06% |
0,01% |
0 |
0,35 |
41 |
2 |
0,07% |
0,03 |
1,2 |
0,02% |
1 |
2,61 |
3,8 |
0,03% |
0,01% |
0 |
21,55 |
42 |
1 |
0,04% |
0,02 |
0,6 |
0,01% |
0 |
1,06 |
4,0 |
0,01% |
0,00% |
0 |
12,86 |
r |
Σn(k) |
|
|
|
σ |
|
χp2 |
|
|
|
|
χG2 |
37 |
2800 |
|
23 |
559,34 |
4,65 |
|
42,40 |
|
|
|
|
73,27 |
Wnioski:
Zestawienie wyników:
|
Seria 1 |
Seria 2 |
Seria 3 |
Rozkład doświadczalny |
n = 1300 r = 14
σ = 2,17 |
n = 35 r = 24
σ = 4,56 |
n = 2800 r = 37
σ = 4,65 |
Rozkład Poissona |
sp = r-2 = 12 Xp2 = 6,47 αp = |
sp = r-2 = 22 Xp2 = 32,15 αp = |
sp = r-2 = 35 Xp2 = 42,40 αp = |
Rozkład Gaussa |
sg = r-3 = 11 Xg2 = 58,96 αg = |
sg = r-3 = 21 Xg2 = 46,33 αg = |
sg = r-3 = 34 Xg2 = 73,27 αg = |
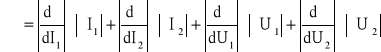
Wyszukiwarka