Wektory

Wektorem położenia lub promieniem wodzącym danej cząstki nazywamy wektor łączący początek układu współrzędnych z punktem w którym znajduje się cząstka.

- W układzie kartezjańskim rzuty wektora położenia na osie układu współrzędnych są równe współrzędnym punktu w którym znajduje się cząstka.

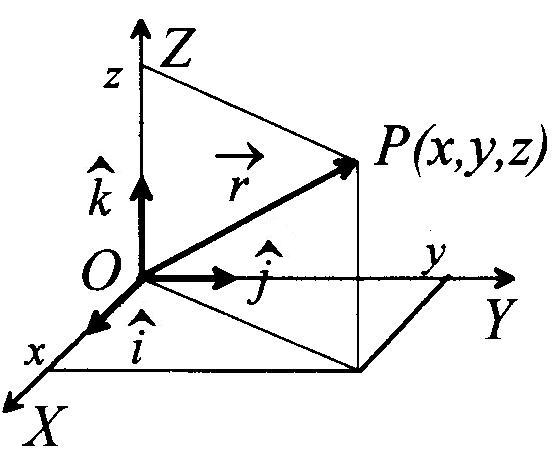
r- to wektor położenia punktu materialnego

• 
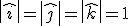
  to wektory jednostkowe (tzw. wersory) w kierunku

osi OX, OY, OZ

x,y,z - to współrzędne wektora położenia w układzie kartezjańskim

- W układzie biegunowym współrzędnymi punktu P, w którym znajduje się cząstka są: r- odległość punktu od początku układu O oraz kąt ϕ między prostą przechodzącą przez punkty O i P a przechodzącą przez początek układu prostą zwaną osią biegunową. Wektor położenia cząstki zadany jest wzorem

r^= 1 . Wzory przejścia ze współrzędnych biegunowych do kartezjańskich :

x= r cos ϕ , y= r sin ϕ . Z kartezjańskich do biegunowych : r = √ x^2 + y^2

ϕ = arc tan y/x

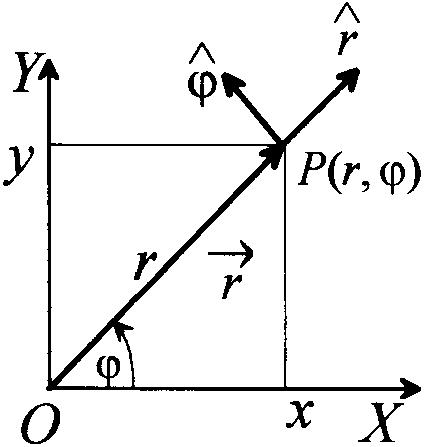
- W układzie cylindrycznym współrzędnymi punktu P w którym znajduje się cząstka są: ρ - długość rzutu wektora połorzenia punktu P na płaszczyznę biegunową, prostopadłą do osi OZ, kąt ϕ między rzutem wektora położenia a osią biegunową i wysokość z punktu nad płaszczyzną biegunową. Wektor położenia cząstki Współrzędne cylindryczne x = ρ cos ϕ y= ρ cos ϕ z = z

Wzory przejścia ze współrzędnych kartezjańskich do cylindrycznych ρ = √ x^2 = y^2 ϕ= arc tan y/x z=z

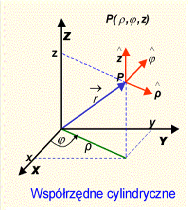
- W układzie sferycznym współrzędnymi punktu P w którym znajduje się cząstka są:

r promienia wodzącego punktu, kąt między promieniem wodzącym a osią OZ i kąt

między rzutem promienia wodzącego na płaszczyznę XOY a osią OX.

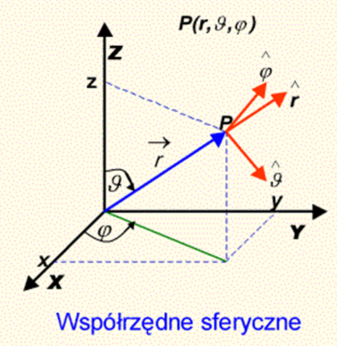
Wektor położenia cząstki
.

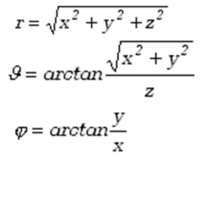
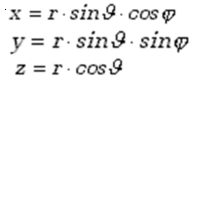
Podstawowe działania na wektorach

Dla wielkości wektorowych można zdefiniować określone działania, jak m.in. mnożenie wektora przez liczbę, dodawanie i odejmowanie wektorów. Iloczyn skalarny oraz wektorowy.

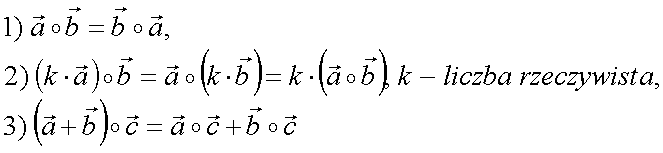
Iloczyn skalarny - operator na przestrzeni liniowej przypisujący dwóm argumentom (wektorom) tej przestrzeni rzeczywistą wartość skalarną.

Własności :

Mnożenie wektorowe jest to operacja, której wynikiem jest nowy prostopadły wektor. Iloczyn wektorowy pary wektorów a i b oznaczamy a × b = v. Reguła prawej dłoni wyznacza kierunek iloczynu wektorowego.

Własności: 1) a × b= - b × a 2) (ka )× b= k (a × b) 3) a ×( b + c )= a × b + a × c 4) a × a= 0

Kinematyka materialnego

Prędkość - to wektorowa wielkość fizyczna wyrażająca zmianę wektora położenia w jednostce czasu. Skalarna wielkość oznaczająca przebytą drogę w jednostce czasu lub tylko wartość prędkości zwana szybkością.

pierwsza pochodna drogi s względem czasu t v = ds/dt.

Przyspieszenie - wektorowa wielkość fizyczna wyrażająca zmianę prędkości w czasie. Przyspieszenie definiuje się jako pochodną prędkości po czasie (jest to miara zmienności prędkości). Przyspieszenie jest wielkością wektorową, gdzie wartość tego wektora jest równa wartości pochodnej prędkości względem czasu w danej chwili. Jeśli przyspieszenie jest skierowane przeciwnie do kierunku prędkości ruchu, to jest czasem nazywane opóźnieniem. a = dv/dt = d²s/dt².

Prędkość kątowa - definicja
Prędkością kątową nazywamy stosunek kąta zakreślonego przez ciało poruszające się po okręgu w danym czasie do tego czasu. Oznacza się ją symbolem ω (mała omega).
ω = Δ α / Δ t

Przyspieszenie kątowe jest wielkością opisującą ruch krzywoliniowy utworzoną analogicznie do przyspieszenia, tylko wyrażoną w wielkościach kątowych. Jest pseudowektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt α, a ω oznacza prędkość kątową, to wartość przyspieszenia kątowego ε określa wzór

Jednostką przyspieszenia kątowego w układzie SI jest jeden radian przez sekundę do kwadratu

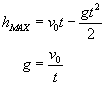
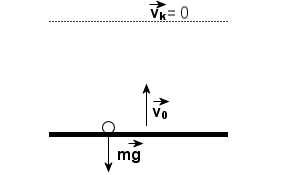
Rzut pionowy do góry to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się ciału prędkość początkową skierowaną do góry. Ruch ciała do góry jest ruchem jednostajnie opóźnionym i właśnie tą częścią ruchu się zajmiemy. Natomiast gdy ciało osiągnie wysokość maksymalną h_MAX następuje swobodny spadek. W tym ruchu jedyną działającą siłą jest siła ciężkości mg, zatem równanie ruchu ciała. gdzie g jest w tym wypadku opóźnieniem (czyli ujemnym przyspieszeniem ziemskim). Zatem rzut pionowy do góry jest ruchem jednostajnie opóźnionym z opóźnieniem równym g.

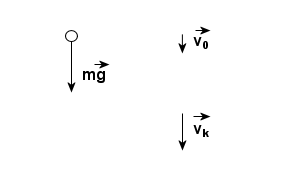
Rzut pionowy w dół to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się ciału prędkość początkową skierowaną pionowo do dołu. Zauważ, że w spadku swobodnym prędkość początkowa jest równa zeru, a w rzucie pionowym w dół prędkość początkowa jest różna od zera. Rzut pionowy do dołu z wysokości h jest ruchem jednostajnie przyspieszonym z przyspieszeniem g i prędkością początkową v₀ różną od zera. W tym ruchu jedyną działającą siłą jest siła ciężkości mg, zatem równanie ruchu ciała

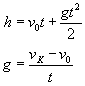
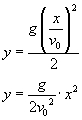
Rzut poziomy to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się ciału prędkość początkową skierowaną poziomo. Rzut poziomy jest więc złożeniem dwóch ruchów:
- w kierunku poziomym ruch ciała jest jednostajny prostoliniowy z prędkością v₀,
- w kierunku pionowym ruch jest jednostajnie przyspieszony bez prędkości początkowej - czyli swobodny spadek (w tym ruch działa na ciało siła ciężkości mg).

Stała A

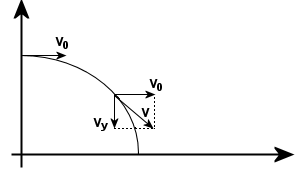
Równanie toru rzutu poziomego.

Czas rzutu poziomego wiec

Zasięg rzutu

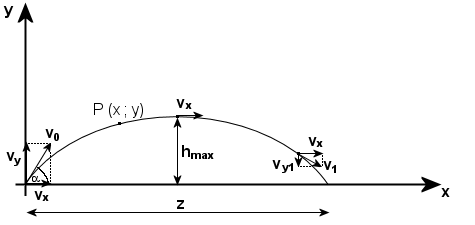
Rzut ukośny to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się ciału prędkość początkową skierowaną do poziomu pod kątem α. Zauważmy, że podobnie jak w rzucie poziomym, tak i w rzucie ukośnym, ciało wykonuje jednocześnie ruch w poziomie i w pionie. Rzut ukośny jest złożeniem dwóch ruchów:
- w kierunku poziomym ruch jednostajny z prędkością v_x,
- w kierunku pionowym ruch jest jednostajnie zmienny
   + do h_MAX jednostajnie opóźniony (rzut pionowy do góry z prędkością v_y),
   + od h_MAX jednostajnie przyspieszony (swobodny spadek) - działa tutaj siła
      ciężkości mg.

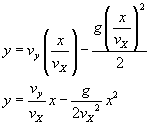
Równanie toru rzutu:

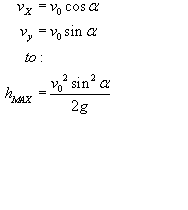
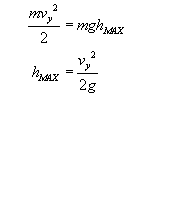
Wysokość Max:

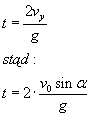
Czas rzutu:

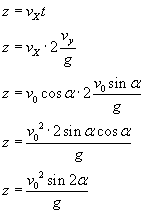
Zasięg rzutu:

Zasady Dynamiki Newtona

I zasada dynamiki (zasada bezwładności): Jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

II zasada dynamiki:

Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa jest różna od zera), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej Współczynnik proporcjonalności jest równy odwrotności masy ciała.

III zasada dynamiki (zasada akcji i reakcji): Oddziaływania ciał są zawsze wzajemne. Siły wzajemnego oddziaływania dwóch ciał mają takie same wartości, taki sam kierunek, przeciwne zwroty i różne punkty przyłożenia (każda działa na inne ciało).

Zasada Zachowania pędu: Jeżeli na układ nie działa żadna siła (lub działające siły się równoważą) to całkowity pęd układu nie ulegnie zmianie 9jest zachowany).

Masa układu złożonego z n ciał wynosi:
m = m1 + m2 + m3 + ... + mn

Pęd całego układu wynosi:
m v = v (m1 + m2 + m3 + ... + mn)

m v = m1 v1 + m2 v2 + m3 v3 + ... + mn vn - zasada zachowania pędu

czyli na ciało nie działa żadna siła i w konsekwencji pęd układu jest zachowany.

Przykład zasady zachowania pędu : Wyskakując z łódki stojącej przy brzegu jeziora uzyskujemy pęd skierowany w stronę lądu. Równocześnie łódka - zgodnie z zasadą zachowania pędu - oddala się nieco od brzegu uzyskując pęd równy co do wartości, lecz przeciwnie skierowany. Wypadkowy pęd układu łódka-człowiek pozostaje nadal równy zeru.

Przykłady III zasady dynamiki newtona Wiosłowanie, lot odrzutowca lub rakiety, zderzenie dwóch piłek, odrzut broni palnej w czasie strzału, niemożliwość podniesienia siebie samego za włosy (albo podniesienia samego siebie razem z krzesłem, na którym siedzisz)zderzenie dwóch piłek, odrzut broni palnej w czasie strzału, niemożliwość podniesienia siebie samego za włosy (albo podniesienia samego siebie razem z krzesłem, na którym siedzisz)

Praca-stałej siły F wyraża się iloczynem skalarnym siły F i wektora przesunięcia s. Praca jest wielkością skalarną. Dżul- symbol(J), to jednostka pracy. Jeden dżul to praca wykonana przez siłę o wartości 1 N przy przesunięciu ciała o 1 m w kierunku równoległym do kierunku działania siły. Co zapisujemy 1J=1Nm

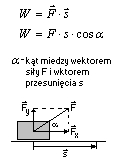
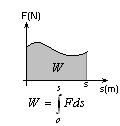
Praca zmienna Niezależnie od przypadku należy policzyć wartość pola pod wykresem F(s).

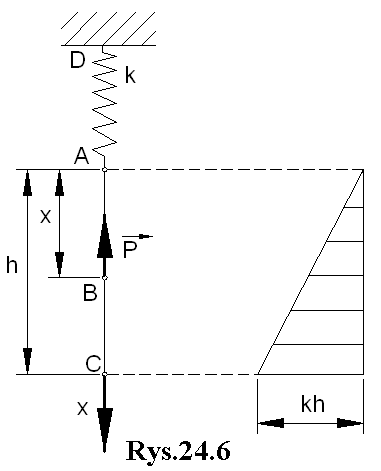
Praca siły sprężystości P = kAB gdzie k jest stałą sprężystości sprężyny. Rzuty siły P na osie O_x, O_y, O_z są równe

A zatem praca elementarna wynosi

Praca siły sprężystości jest równa

Siły zachowawcze - są to takie siły, dla których praca po dowolnej drodze między (dowolnymi) punktami A i B nie zależy od drogi (krzywej toru po którym porusza się ciało) i wyraża się przez zmianę energii potencjalnej ciała w trakcie ruchu od A do B: Ep(A)‐Ep(B):

Układ Punktów Materialnych

Środek masy Rozważmy dwa ciała o masach m₁ i m₂ położone na osi X w punktach x₁ i x₂ odległe od siebie o l = x₂ - x₁ . Punkt S, który dzieli odcinek l w stosunku odwrotnie proporcjonalnym do mas tych ciał nazywamy środkiem masy układu dwóch ciał (punktów materialnych). Zatem:

Jeżeli przez x_S oznaczymy współrzędną środka masy, to:

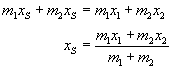
Uogólniony na n mas

W celu określenia środka masy w przestrzeni należy

podać wszystkie trzy współrzędne. Współrzędne y_S i z_S wyrażają się analogicznymi wzorami do x_S

Prędkość układu Środek masy może być w spoczynku lub poruszać się podczas ruchu poszczególnych ciał układu. Zapytajmy, jaka jest prędkość środka masy v_S, gdy znane są prędkości i masy ciał układu. Pisząc dwa powyższe równania dla dwóch różnych chwil czasu i odejmując je od siebie stronami, otrzymamy:

Dzieląc obie strony równania przez Δt = t₂ - t₁ i uwzględniając, że prędkość środka

Masy wynosi
oraz biorąc prędkości poszczególnych ciał otrzymamy:

Przyspieszenie układu : Jak zachowuje się środek masy, gdy na układ działają siły zewnętrzne? Środek masy uzyskuje wtedy przyspieszenie a_S, które można obliczyć z drugiej zasady dynamiki Newtona: gdzie F oznacza sumę wektorową zewnętrznych sił działających na wszystkie ciała układu. Zatem środek masy układu zachowuje się tak, jak gdyby cała masa układu znajdowała się w punkcie środka masy i jak gdyby wszystkie siły działające na ciała układu były przyłożone do tego punktu.

Pęd układu - Pęd układu punktów materialnych -suma wektorowa pędów wszystkich punktów. Przyrost pędu układu punktów materialnych jest równy popędowi wypadkowej sił zewnętrznych. Pęd układu punktów materialnych pozostaje niezmienny, jeżeli siły działające na układ równoważą się.

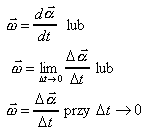
Prędkość kątowa obracającej się bryły to charakterystyczna dla ruchu obrotowego wielkość określająca kąt zakreślany przez bryłę w określonym czasie.

Każdy punkt obracającej się bryły ma inną prędkość liniową,

natomiast prędkość kątowa wszystkich punktów bryły jest taka

sama. Punkt odległy od osi obrotu o r ma prędkość liniową v taką, że v = r ω

Należy pamiętać, że wektor prędkości kątowej jest prostopadły do płaszczyzny ruchu.

Przyspieszenie Kątowe obracającej się bryły określamy jako zmianę prędkości kątowej tej bryły w czasie.

Każdy punkt obracającej się bryły ma inne przyspieszenie liniowe, natomiast przyspieszenie kątowe wszystkich punktów bryły jest takie samo. Punkt odległy od osi obrotu o r ma przyspieszenie liniowe a takie, że a = ε r

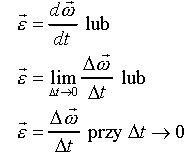
Zasady dynamiki w ruchy obrotowym bryły sztywnej

Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od rozmieszczenia masy w ciele. Moment bezwładności ma wymiar . Zwykle mierzy się go w kg·m².

Moment bezwładności punktu materialnego jest iloczynem jego masy i kwadratu odległości od osi obrotu:

gdzie:

- masa punktu;

- odległość punktu od osi obrotu.

Moment bezwładności ciała składającego się z
punktów materialnych jest sumą momentów bezwładności wszystkich tych punktów względem obranej osi obrotu:

Dla ciał o ciągłym rozkładzie masy sumowanie we wzorze na moment bezwładności przechodzi w całkowanie. Niech ciało będzie podzielone na nieskończenie małe elementy o masach
, oraz niech
oznacza odległość każdego takiego elementu od osi obrotu. W takim przypadku moment bezwładności określa wzór:

gdzie całkowanie odbywa się po całej objętości
ciała.

Za pomocą momentu bezwładności
bryły sztywnej, obracającej się względem pewnej osi z prędkością kątową
względem tej osi, można wyrazić energię kinetyczną
tej bryły

Twierdzenie Steinera Mówi że, moment bezwładności bryły sztywnej względem dowolnej osi jest równy sumie momentu bezwładności względem osi równoległej do danej i przechodzącej przez środek masy bryły oraz iloczynu masy bryły i kwadratu odległości między tymi dwiema osiami, co można wyrazić wzorem

gdzie:

- moment bezwładności względem osi przechodzącej przez środek masy,

- moment bezwładności względem osi równoległej do pierwszej osi,

- odległość między osiami, I = Io + ma^2

- masa bryły.

Moment bezwładności osiąga minimalną wartość, gdy oś przechodzi przez środek masy.

MOMENT PĘDU

Moment pędu (inaczej kręt) wielkość fizyczna opisująca ruch ciała, zwłaszcza ruch obrotowy.

W tradycyjnej matematyce moment pędu jest wielkością wektorową (pseudowektor). Moment pędu punktu materialnego względem zadanego punktu określony jest zależnością składowych

gdzie:

- moment pędu punktu materialnego,

- wektor łączący punkt, względem którego określa się moment pędu i punkt ciała,

- pęd punktu materialnego,

Powyższy wzór można wyrazić:

gdzie: θ_{r, p} jest kątem między
i

Dla ciała obracającego się:

gdzie:

I - moment bezwładności ciała,

- prędkość kątowa.

Moment siły (moment obrotowy) siły F względem punktu O jest to iloczyn wektorowy promienia

wodzącego r, o początku w punkcie O i końcu w punkcie przyłożenia siły, oraz siły F:

Wektor momentu siły jest wektorem zaczepionym w punkcie O, a jego kierunek jest prostopadły do

kierunku płaszczyzny wyznaczonej przez wektor F i promień wodzący r. Jednostką momentu siły

jest Nm (niutonometr).

Moment pędu a moment siły- pochodna momentu pędu L bryły względem czasu t jest równa momentowi siły M działającej na tę bryłę.

Druga zasada dynamiki ruchu obrotowego - sformułowanie II zasady dynamiki dla ruchu obrotowego bryły sztywnej wokół stałej (nie obracającej się w przestrzeni) osi. Dotyczy np. sytuacji, gdy oś obrotu jest wymuszona przez zewnętrzne więzy. Mówi ona, że jeśli na pewne ciało, o momencie bezwładności względem tej osi równym I, działają zewnętrzne siły, które wywierają na to ciało wypadkowy moment siły M, to w wyniku tego ciało będzie obracać się z przyspieszeniem kątowym takim, że:

Moment siły M i przyspieszenie kątowe ε są wektorami osiowymi (pseudowektorami) a ich kierunek i zwrot są takie same.

Granicznym przypadkiem drugiej zasady dynamiki dla ruchu obrotowego jest sytuacja, gdy wypadkowy moment sił działających na ciało równy jest 0 (pierwsza zasada dynamiki dla ruchu obrotowego). Ze wzoru wynika, że wówczas przyspieszenie kątowe również będzie równe 0 a bryła obracać się będzie ze stałą prędkością kątową.

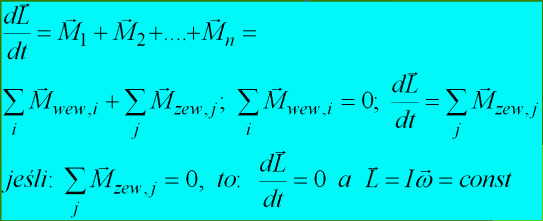
Zasada zachowania momentu pędu- moment pędu układu na który nie działają momenty sił zewnętrznych lub działające momenty sił się równoważą pozostaje stały.

Przykłady : 1) na przykład łyżwiarz, który jak rozkprostowuje ręce, to się obraca wolniej (piruet), a jak trzyma ręce przy sobie, to szybciej 2) wszelkie takie ruch obrotowe, np. trzymasz coś na nitce i obracasz ręką, jak skracasz nitkę, to zaczyna ci się to szybciej obracać

Praca w ruchu obrotowym

praca elementarna sił działających na ciało sztywne pozostające w ruchu obrotowym dookoła nieruchomej osi jest równa iloczynom sumy momentów tych sił względem osi obrotu i elementarnego kąta obrotu.

Elementarna praca wszystkich sił działających na ciało sztywne jest równa

Dla to

Stany równowagi w mechanice

Równowaga w mechanice - stan układu mechanicznego, w którym wszystkie punkty układu pozostają w spoczynku względem wybranego układu odniesienia.

Badaniem stanów równowagi zajmuje się dział fizyki zwany statyką.

Dla brył sztywnych znajdujących się w polu grawitacyjnym, wyróżnia się następujące stany równowagi oraz warunki ich występowania:

równowaga trwała (stabilna) - ma miejsce, kiedy środek ciężkości jest położony w najniższym możliwym punkcie, a przy odchyleniu ciała powstaje moment sił ciężkości względem punktu podparcia lub zawieszenia powodujący jego powrót do położenia pierwotnego, w którym to położeniu energia potencjalna ma najmniejszą wartość.

równowaga chwiejna - ma miejsce, kiedy środek ciężkości znajduje się powyżej punktu podparcia, a przy odchyleniu ciała powstaje moment sił ciężkości wychylających je w taki sposób, że przemieszcza się ono, zmniejszając swoją energię potencjalną, do momentu osiągnięcia równowagi trwałej (stabilnej), kiedy energia potencjalna osiąga najmniejszą wartość.

równowaga obojętna - ma miejsce wtedy, gdy energia potencjalna ma taką samą wartość we wszystkich położeniach ciała, a przy odchyleniu ciała względem położenia równowagi, energia potencjalna nie zmienia się.

równowaga metastabilna - ma miejsce wtedy, kiedy ciało zajmuje położenie, w którym energia potencjalna osiąga lokalne minimum (ciało otoczone jest barierą potencjału). Przy wytrąceniu ciała z położenia równowagi niewielką siłą, powraca ono do położenia pierwotnego, natomiast przy wytrąceniu większą siłą ciało znajduje nowe położenie o mniejszej energii potencjalnej.

Zasady Statyki

- Zasada pierwsza (zasada równoległoboku). Działanie dwóch sił P₁ i P₂ można zastąpić działaniem jednej siły R, działającej na ten sam punkt, będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P₁ i P₂

- Zasada druga. Jeżeli do ciała przyłożone są dwie siły, to równoważą się one tylko wtedy, gdy mają tę samą linię działania, te same wartości liczbowe i przeciwne zwroty. Aby siły te równoważyły się, muszą być spełnione zależności

- Zasada trzecia. Skutek działania dowolnego układu sił przyłożonego do ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. układ zerowy. Wynika stąd następujący wniosek: każdą siłę działającą na ciało sztywne można przesunąć dowolnie wzdłuż jej linii działania.

- Zasada czwarta (zasada zesztywnienia). Jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne), identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do równowagi ciała odkształcalnego.

- Zasada szósta (zasada oswobodzenia od więzów). Każde ciało nieswobodne można myślowo oswobodzić z więzów, zastępując ich działanie reakcjami, a następnie rozważać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów).

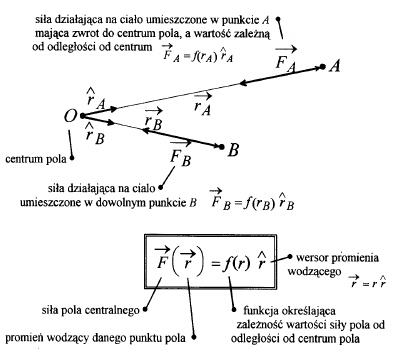
Siła Centralna Jest to siła, której wartość zależy tylko od odległości od źródła. Gdy źródło znajduje się w początku układu, to siłę centralną można zapisać w postaci

gdzie F(r) określa wartość siły a wektor
jest wersorem wektora
.

Siły centralne zawsze są zachowawcze, mają potencjał zależny tylko od r i spełniają zasadę zachowania momentu pędu.

Siłami centralnymi są np. siła grawitacji kuli lub siła elektrostatyczna ładunku punktowego.

Pole Grawitacyjne

Prawo powszechnego ciążenia, zwane także prawem powszechnego ciążenia Newtona, głosi, że każdy obiekt we wszechświecie przyciąga każdy inny obiekt z siłą, która jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jest to ogólne prawo fizyczne, bazujące na empirycznych obserwacjach Newtona, które nazwał on indukcją

Zależność przyspieszenia grawitacyjnego od wysokości :

gh=

Potencjałem pola grawitacyjnego w danym punkcie nazywamy stosunek energii potencjalnej, jaką ma w tym punkcie umieszczone tam ciała, do masy tego ciała.

jednostka: [V]=J/kg

Energia pot. i praca Ciało o masie m umieszczone w danym punkcie pola ma energię potencjalną, która jest równa pracy, jaką wykonają siły pola, aby przenieść ciało z nieskończoności do tego punktu:

gdzie M to masa ciała będącego źródłem pola. Im dalej znajduje się

ciało od źródła pola, tym jego energia potencjalna jest bliższa zeru.

Pierwsza prędkość kosmiczna to najmniejsza pozioma prędkość, jaką należy nadać ciału względem przyciągającego je ciała niebieskiego, aby ciało to poruszało się po zamkniętej orbicie. Z tak określonych warunków wynika, że dla ciała niebieskiego o kształcie kuli, orbita będzie orbitą kołową o promieniu równym promieniowi planety. Ciało staje się wtedy satelitą ciała niebieskiego.

G - stała grawitacyjna,

M - masa ciała niebieskiego,

m - masa rozpędzanego ciała,

R - promień ciała niebieskiego.

Druga prędkość kosmiczna to prędkość, jaką należy nadać obiektowi, aby opuścił na zawsze dane ciało niebieskie poruszając się dalej ruchem swobodnym, czyli jest to prędkość, jaką trzeba nadać obiektowi na powierzchni tego ciała niebieskiego, aby tor jego ruchu stał się parabolą lub hiperbolą . Obliczamy ją porównując energię obiektu znajdującego się na powierzchni oraz w nieskończoności. Energia w nieskończoności równa jest 0 (zarówno kinetyczna, jak i potencjalna pola grawitacyjnego), zatem na powierzchni sumaryczna energia też musi się równać 0

M - masa ciała niebieskiego,

m - masa wystrzeliwanego ciała,

v - prędkość początkowa,

R - promień ciała niebieskiego.

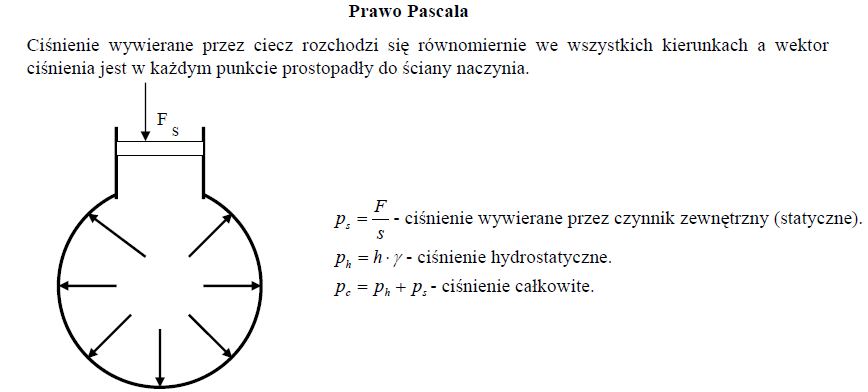
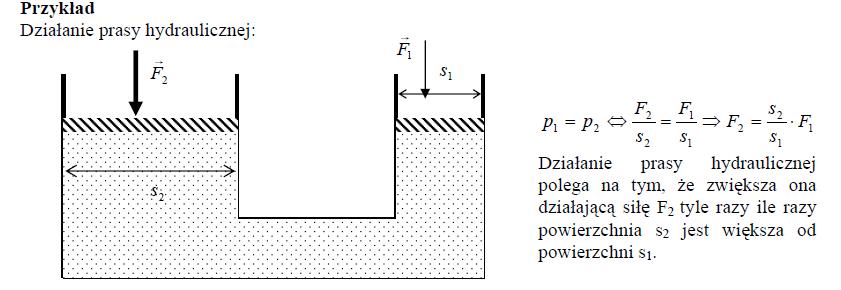
Prawo Archimedesa - siła wyporu działająca na ciało zanurzone w płynie jest równa ciężarowi płynu wypartego przez to ciało tzn: że siła wyporu jest tym większa, im cięższy jest płyn - większa siła wyporu jest w wodzie, niż w powietrzu i większa w rtęci, niż w wodzie. siła wyporu jest tym większa, im większe (rozmiarami, objętością) jest ciało (a przynajmniej jego zanurzona część)

F_wyporu = ρ_płynu ∙g ∙V_zanurzona

ρ_płynu - gęstość płynu (cieczy, gazu) w którym zanurzone jest ciało -  [w układzie SI w kg/m³]
V_zanurzona - objętość tej części ciała, która jest zanurzona w płynie (w układzie SI w m³)
g - przyspieszenie ziemskie  [w układzie SI w m/s²]

Napięcie powierzchniowe - Miarą napięcia powierzchniowego jest praca, jaką trzeba wykonać, by utworzyć jednostkową powierzchnię cieczy, co można wyrazić wzorem:

γ (używa się też oznaczenia σ) - napięcie powierzchniowe,

ΔW - praca potrzebna do utworzenia powierzchni ΔS,

ΔS - pole powierzchni.

Napięcie powierzchniowe silnie zależy od temperatury cieczy. Zmniejsza się wraz ze wzrostem temperatury i spada aż do zera w temperaturze krytycznej.

Istnieją wzory empiryczne określające zależność napięcia powierzchniowego od temperatury.

Zmiana Ciśnienia wywołana istnieniem menisku

Zakrzywiona powierzchnia cieczy wytwarza ciśnienie określone wzorem zwanym wzorem Laplace'a (en:Young-Laplace Equation):

.

gdzie dA zmiana powierzchni cieczy, wywołana dV zmianą objętości.

Z zależności tej wynika:

Dla płaskiej powierzchni dlatego ciśnienie w cieczy i na zewnątrz jest takie same.

Dla powierzchni kuli (sfera), czyli w kropli .

W bańce o cienkich ściankach , bo bańka ma dwie ścianki.

Prawo ciągłości strugi Przez każdy z przekrojów poprzecznych naczynia w którym płynie ciecz przepływa w tym samym czasie taka sama objętość cieczy V1=V2 ⇔ V=const

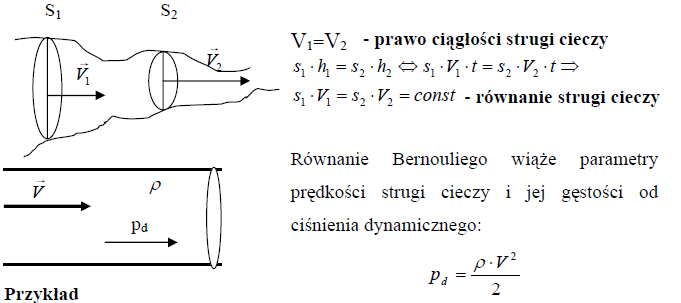
Jeszcze jeden przykład z życia wzięty. Jeśli przytkniemy 2 kartki papieru do obydwóch policzków i dmuchniemy pomiędzy nie, to paradoksalnie zaczną one do siebie przylegać. Wytłumaczenie tego zjawiska jest proste. Strumień wydmuchiwanego powietrza ma ciśnienie dynamiczne, a więc ciśnienie statyczne (działające w bok - na kartki) będzie mniejsze od tego, które działa na kartki z zewnątrz (od statycznego powietrza). Zatem ciśnienie zewnętrzne przeważy i dlatego kartki przylgną do siebie.

---