Rozwiązywanie numeryczne równań nieliniowych

Wyznaczanie przedziałów izolacji. Niech będzie dane nieliniowe równanie algebraiczne

,

przy czym funkcja
jest ciągła w przedziale domkniętym
.

Zadanie polega na odnalezieniu takich przedziałów

,

które zawierają pojedyncze pierwiastki równania
. W tym celu będziemy obliczać wartości funkcji
od punktu
do punktu
z krokiem
. Jeżeli w sąsiednich punktach funkcji ma przeciwny znaki

,

to przedział
zawiera pierwiastek.

Zawsze zostaje problem wybory wielkości przedziału
. W związku z tym powyższy algorytm uzupełniamy dodatkowo sprawdzaniem warunku

.

W przeciwnym razie krok należę dzielić na pół, dopóki nie przekonamy się, że przedział
nie zawiera pierwiastka.

Dotoczymy schemat blokowy poszukiwania przedziałów zawierających pierwiastki.

Metoda równego podziału. Dane jest nieliniowe równanie algebraiczne

,

przy czym funkcja
jest ciągła w przedziale domkniętym
oraz zachodzi nierówność

.

Twierdzenie (Bolzano - Cauchy'ego). Jeśli funkcja ciągła
ma na końcach przedziału domkniętego
wartości różnych znaków, to wewnątrz tego przedziału istnieje co najmniej jeden pierwiastek równania
.

W celu znalezienia pierwiastka równania
zawartego w przedziale
dzielimy ten przedział na dwie połowy. Jeśli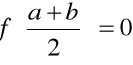
, to szukany pierwiastek wynosi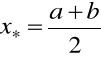
. Jeżeli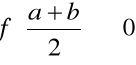
, to z przedziałów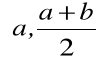
i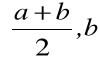
wybieramy ten, na końcach którego funkcja
ma różne znaki. Następnie połowimy nowy zawężony przedział i powtarzamy czynności itd.

W ten sposób albo pierwiastek dokładny
, albo ciąg podprzedziałów

,
, … ,
, …

przy czym

,

oraz

,

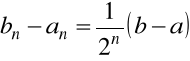
Ponieważ
, to z poprzedniego wyrażenia wynika istnienie wspólnej granicy
.

Oto schemat blokowy algorytmu

Metoda siecznych. Zamiast dzielić przedział
na dwie połowy podzielimy go w stosunku

.

W interpretacji geometrycznej metoda siecznych oznacza zastąpienie krzywej
przez cięciwę łączącą punkty

i
.

Teoretycznie możliwy cztery różne przypadki podane na rysunku. Punkt, w którym wartość funkcji
ma taki sam znak, jak i druga pochodna
, pozostaje nieruchomy.

Na rysunkach

nieruchomy jest punkt
.

Wtedy otrzymujemy rosnący ciąg ograniczony

,
,

Na rysunkach

nieruchomy jest punkt
.

Wtedy otrzymujemy malejący ciąg ograniczony

,
,

Oto schemat blokowy odpowiedniego algorytmu dla metody siecznych.

Metoda stycznych. Zakładając, że
oraz że pierwsza pochodna
i druga pochodna
są ciągłe i nie zmieniają znaku w przedziale domkniętym
, pierwiastek równania
można znaleźć metodą Newtona według wzoru

,

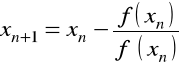
Jako przybliżenie zerowe wybieramy ten punkt, w którym wartości funkcji
i druga pochodna
jednakowe znaki. Na przykład, punkt
na rysunkach

lub punkt
dla poniższych wykresów

Oto schemat blokowy odpowiedniego algorytmu.

Przykład. Znaleźć pierwiastek kwadratowy z liczby
(Babilon), tj. rozwiązać równanie

.

Powyższy wzór Newtona przybiera postać

.

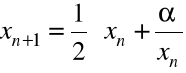
Metoda iteracji. Metoda ta oparta jest na pojęciu odwzorowania zwężającego.

Definicja. Odwzorowanie
przestrzeni metrycznej
w siebie

,

nazywamy odwzorowaniem zwężającym, gdy istnieje taka liczba
(
), że

,

dla dowolnych
.

Odwzorowanie zwężające jest ciągłym, ponieważ

i
,

wówczas

a więc
.

Twierdzenie Banacha. Niech
będzie odwzorowaniem zwężającym przestrzeni metrycznej zupełnej
w siebie. Wtedy istnieje jeden i tylko jeden punkt
taki, że

Ponadto, jeżeli
jest dowolnym punktem przestrzeni oraz

,
,

to

i zachodzi nierówność

,

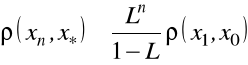
Twierdzenie Banacha podaje metodę przybliżonego rozwiązywania równania o postaci

za pomocą ciągu

,
,

która znana jak metoda iteracji albo metoda kolejnych przybliżeń.

Twierdzenie. Niech funkcja
będzie określona i różniczkowalna w przedziale domkniętym
i niech jej wartości należą do tego przedziału. Wtedy jeśli istnieje ułamek właściwy
taki, że

,

to proces iteracyjny
jest zbieżny niezależnie od przybliżenia początkowego
, zaś wartość graniczna

jest jedynym pierwiastkiem równania
w przedziale domkniętym
.

Więc idea metody iteracji jest sprowadzić każde równanie
do równoważnej postaci
i następnie sprawdzić warunki poprzedniego twierdzenia.

Interpretacja geometryczna podana na poniższych rysunkach.

Na rysunkach

metoda iteracyjna jest zbieżna (
), wówczas na rysunkach

metoda iteracyjna jest rozbieżna (
).

Oto schemat blokowy algorytmu

Uwaga

Błąd bezwzględny jest dwa mniejszy długości ostatniego przedziału

T

N

N

Koniec!

Drukuj

X, ΔX

N

B:=C

F(A)F(C)<0

A:=C

F(C)=0

X:=(A+B)/2

ΔX:=(B-A)/2

Drukuj

C - pierwiastek

Koniec!

T

C:=(A+B)/2

Podaj

A. B, ε

Początek

T

Początek

N

Koniec!

T

N

T

Drukuj

x₁, x₂

y₁y₂<0

Podaj

A. B, ε

N

y₂=F(x₂)

x₂<b

x₁:=x₂

x₂:=x₁-h

y₁:=y₂

x₁:=a

x₂:=x₁+h

y₁=f(x₁)

Podaj

a, b, h

Początek

N

Koniec!

Drukuj

X₁ - pierwiastek

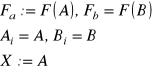
Koniec!

T

Podaj

X₀, ε

Drukuj

X - pierwiastek

Koniec!

N

N

T

T

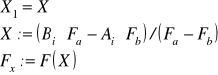
Drukuj

X₁ - pierwiastek

Początek

Podaj

X₀, ε

Początek