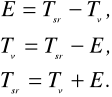Ćwiczenie 1

Transformacje pomiędzy układami współrzędnych

Zadanie: Współrzędne prostokątne (X,Y,Z) w układzie globalnym WGS84 przeliczyć na

elipsoidalne (B,L,h) odniesione do elipsoidy WGS84, a następnie znając parametry

transformacji 7-parametrowej pomiędzy układami, przeliczyć współrzędne (X,Y,Z)

w układzie WGS84 na współrzędne prostokątne, odniesione do układu "Krasowski

42". Otrzymane współrzędne przeliczyć na B,L,h odniesione do elipsoidy "42".

Wzory i dane:

,

,

.

zamiana odwrotna:

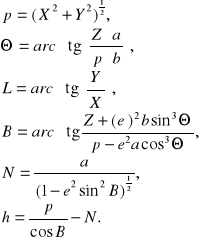
przy czym:

elipsoida WGS84 elipsoida Krasowskiego 42

a = 6378137.0 m a = 6378245.0

e
= 0.0066943799013 e
= 0.006693421623

(e)
= 0.00673949674227 (e)
= 0.006738525415

b = 6356752.3142 m b = 6356863.01877 m

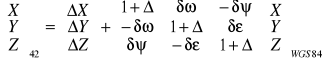
przy czym należy przyjąć następujące parametry transformacji:

X= -23.0 m

Y=124.5 m

Z= 82.5 m

ၤၷ= 0.0 + 0.1 nr na liście

= 2.0

= -2.5

= 210
+ 0.110
nr na liście

Uwaga! Składowe transformacji kątowe należy zamienić na odpowiadające im wartości liniowe (czynność tę wykonujemy w trakcie mnożenia macierzy transformującej - mnożąc współrzędne X,Y,Z wyrażone w układzie WGS84 przez odpowiednie kąty, dzielimy wynik przez ၲ sekundowe = 206264.806 sekund łuku).

Współrzędne:

Punkt X
Y
Z

1 3524523.4793 1329693.7456 5129846.4049

2 3592275.2039 1326519.6154 5083787.0189

3 3648845.9694 1359140.2015 5034919.5360

Przykład opracował: dr inż. Jacek Lamparski

Ćwiczenie nr 2

Układy współrzędnych używane w astronomii geodezyjnej

W astronomii geodezyjnej używa się najczęściej następujących układów współrzędnych:

• układ horyzontalny,

• układ równikowy ekwinokcjalny,

• układ równikowy godzinny.

Układ współrzędnych horyzontalnych

Na rysunku pokazane są dwie współrzędne - wysokość horyzontalna h lub odległość zenitalna z oraz azymut - kąt poziomy, mierzony w horyzoncie od kierunku północy (uwaga! w astronomii azymut jest mierzony od kierunku południa). Wiadomo, że:

h = 90⁰ - z,

z = 90⁰ - h.

Taki układ współrzędnych jest realizowany w każdym instrumencie geodezyjnym. Płaszczyzną odniesienia dla pomiaru wysokości horyzontalnej jest płaszczyzna horyzontu, określana poprzez dokładne spoziomowanie instrumentu.

Drugim układem odniesienia jest układ współrzędnych równikowych ekwinokcjalnych. Jest on tzw. układem inercjalnym (niezależnym), ponieważ nie jest związany z obracającą się Ziemią, a z „nieruchomymi” względem Ziemi gwiazdami. Płaszczyzną odniesienia jest płaszczyzna równika niebieskiego, powstała jako przecięcie nieskończenie odległej sfery niebieskiej z płaszczyzna poprowadzoną przez równik Ziemi. Od tej płaszczyzny mierzona jest deklinacja ၤ . Punktem odniesienia dla określenia drugiej współrzędnej jest punkt zwany punktem równonocy (ekwinokcjum) lub tzw. punkt Barana (od gwiazdozbioru Barana, w którym się znajduje na sferze niebieskiej). Ta współrzędna jest nazwana rektascenzją i oznaczona jako ၡ. Tak więc mamy w tym układzie dwie współrzędne:

ၡ - rektascenzja,

ၤ - deklinacja.

Układ współrzędnych równikowych ekwinokcjalnych

Trzecim układem wiążącym układ równikowy ekwinokcjalny z obracającą się Ziemią jest układ równikowy godzinny. Jedną współrzędną jest deklinacja ၤ, drugą kąt godzinny t.

Kąt godzinny jest kątem mierzonym w płaszczyźnie równika niebieskiego odwrotnie do ruchu wskazówek zegara od płaszczyzny tzw. „południka miejscowego” do płaszczyzny południka danej gwiazdy.

Południk miejscowy jest kołem wielkim leżącym na sferze niebieskiej - przechodzi on przez punkty: północny biegun Świata, zenit miejsca obserwacji, punkt południa w horyzoncie, południowy biegun Świata, nadir oraz punkt północy w horyzoncie.

Układ współrzędnych równikowych godzinnych

Zależności pomiędzy układami współrzędnych można znaleźć, rozwiązując wzorami trygonometrii sferycznej tzw. trójkąt paralaktyczny, który powstaje poprzez nałożenie różnych układów na sferę niebieską:

Trójkąt paralaktyczny

Wzory, służące do przeliczania z układu równikowego do horyzontalnego są następujące:

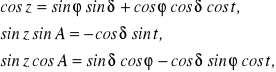
przy czym w wyniku podzielenia wzoru drugiego przez trzeci uzyskujemy wzór na tg A, który jest używany w praktyce do obliczenia azymutu gwiazdy Biegunowej (Północnej) w trakcie wyznaczania azymutu astronomicznego celu ziemskiego metodą „kąta godzinnego Biegunowej”.

Wzory do zamiany współrzędnych azymutalnych na równikowe godzinne są nastepujące:

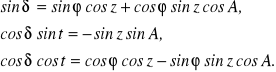
Widzimy, że w obliczeniach niezbędna jest znajomość szerokości geograficznej miejsca obserwacji ၪ. Widzimy również, że ważna jest zależność:

ၑ = ၡ+ t

Zadanie: mając szerokość ၪ miejsca obserwacji, równą 53⁰ 45^' , długość geograficzną miejsca obserwacji ၬ = 1^h21^m52.^s8 oraz współrzędne gwiazdy, równe ၡ = 2^h 32^m 29.^s80 i ၤ = 89⁰15^' 26.^''91, oblicz współrzędne h i A w momencie obserwacji T = 20^h 20^m 00.^s0 + n· 5^m czasu środkowoeuropejskiego. Wykonaj zamianę odwrotną.

(Wskazówka: w celu obliczenia kata godzinnego t, przelicz czas środkowoeuropejski na czas gwiazdowy miejscowy ၑ_Olsztyna = ၑ_Greenwich + ၬ ).

Ćwiczenie nr 3

Przeliczanie czasu słonecznego średniego na gwiazdowy średni i odwrotnie

Przeliczanie czasu słonecznego, który z definicji ma sekundę dłuższą od sekundy gwiazdowej, na czas gwiazdowy, może być zrealizowane na mocy zależności:

0^h ၄T T Czas słoneczny

0^h ၑ_o ၄ၑ ၑ

Czas gwiazdowy

ၑ

Wartość czasu gwiazdowego Greenwich oznaczona jako ၑ_o podawana jest w każdym Roczniku Astronomicznym (tabela pt. Czas gwiazdowy Greenwich o 0 godzinie czasu uniwersalnego).

Interwał ၄ၑ czasu gwiazdowego należy zamienić na odpowiadający mu interwał czasu słonecznego. Czynność tę można wykonać przy pomocy tablic pomocniczych, zamieszczonych również w RA lub ręcznie, wiedząc, że stosunek zamiany sekund gwiazdowych na słoneczne lub odwrotnie jest stałą liczbą.

0.9972695654 lub odwrotnie 1.0027379103.

Przykład:

Przeliczyć moment 13h 30^m 00.^s000 w dniu 3 kwietnia 1998, czasu słonecznego średniego (czas wschodnioeuropejski) na gwiazdowy średni Greenwich i odwrotnie.

3 kwietnia 1998 roku, godz. 13
30
00.
000

- różnica czasów strefowych -2

---------------------------------------

Czas Greenwich (Uniwersalny) 11
30
00.
000 TU

+ redukcja 1^m 53.^s 349 red.

--------------------------------------

11 ^h 31^m 53.^s 349 ၄ၑ

+ ၑ_o 12 ^h 44 ^m 29.^s 946 ၑ_o

--------------------------------------

Czas gwiazdowy Greenwich 00^h 16 ^m 23.^s 295 ၑ

Zamiana odwrotna:

Czas gwiazdowy Greenwich 00
16
23.
295 ၑ

- ၑ_o -12
44
29.
946 ၑ_o

---------------------------------------

၄ၑ 11
31
53.
349 ၄ၑ

- redukcja 1^m 53.^s 349 red.

--------------------------------------

11
30
00.
000 ၄ၑ

+ różnica czasów strefowych +2

--------------------------------------

3 kwietnia 1998 roku, godz. 13
30
00.
000

Przeliczanie czasu słonecznego średniego na prawdziwy i odwrotnie

Czas słoneczny prawdziwy jest związany z rzeczywistym położeniem Słońca na sferze niebieskiej w danym momencie. Różnica pomiędzy położeniem średnim (wyliczonym a priori) a rzeczywistym, zwana równaniem czasu sięga od minus kilkunastu do plus kilkunastu minut w ciągu roku.

Wartość równania czasu (E+12
), powiększona o 12
jest podawana w Roczniku Astronomicznym (str. 10-17) w tabeli Słońce. Jest ona podawana na 0
czasu TDT (dynamiczny czas ziemski), związanego z czasem TU zależnością:

T jest wartością określaną w pełnych sekundach i wynosi:

- w roku 1998 - 63 s,

- w roku 1997 - 62 s,

- w roku 1996 - 62 s,

- w roku 1995 -

- w roku 1994 - 59 s,

- w roku 1993 - 59 s,

- w roku 1992 - 58 s,

- w roku 1991 - 58 s,

- w roku 1990 - 58 s,

- w roku 1989 - 58 s,

- w roku 1985 - 55 s.

Tak więc:

Przeliczenie czasu słonecznego średniego na czas słoneczny prawdziwy:

Mamy czas letni, czyli wschodnioeuropejski;

3 kwietnia 1994 roku, godz. 13
30
00.
000

- różnica czasów strefowych -2

---------------------------------------

Czas Greenwich - uniwersalny 11
30
00.
000 TU

Tworzymy czas TDT 59.
000 T

----------------------------------------

11
30
59.
000 TDT

Moment czasu TDT zamieniamy na ułamek dziesiętny doby (korzystamy z tabeli pomocniczej w R.A. na str. 104).

11
30
59.
000 = 0.
250000 (6
)

0. 229167 (5
30
)

0. 000683 (59
)

--------------------------

0.
479850 Na tę część doby interpolujemy liniowo wartość (E+12
)

11
56
31.
650

+ 8.
460

-------------------------

11
56
40.
110

11
30
00.
000 TU

- 11
56
40.
110 (E+12
)

----------------------------

11
33
19.
890

Otrzymaliśmy wartość czasu słonecznego prawdziwego, odpowiadającą czasowi słonecznemu średniemu.

Zamiana czasu słonecznego prawdziwego na czas słoneczny średni:

Posiadamy tylko moment czasu słonecznego prawdziwego:

11
33
19.
890

Obliczenia wykonujemy metodą kolejnych przybliżeń, biorąc w pierwszym przybliżeniu, że:

Wówczas:

11
33
19.
890

59.
000 T

--------------------------

11
34
18.
890 TDT
na ten moment

interpolujemy wartość

(E+12
)

11
34
18.
890 = 0.
250000 (6
)

0. 231944 (5
34
)

0. 000208 (18
)

0. 000001 (0.
)

--------------------

0. 482163 11
56
31.
650

+ 8.
500

---------------------------

11
56
40.
150 (E+12
)

11
33
19.
890

11
56
40.
150 +(E+12
)

--------------------------

23
30
00.
040

- 12

---------------------------

11
30
00.
040

11
30
00.
040
Tworzymy dynamiczny czas ziemski

+ 59.
000

---------------------------

11
30
59.
040 TDT
Na ten moment interpolujemy po raz drugi

wartość równania czasu

11
30
59.
= 0.
250000 (6
)

0. 229167 (5
30
)

0. 000683 (59
)

0. 000000 (0.
040)

---------------------------

0. 479850

11
56
31.
650

+ 8.
460

--------------------------

11
56
40.
110 (E+12
)

11
33
19.
890

11
56
40.
110 (E+12
)

-------------------------

23
30
00.
000

- 12

--------------------------

11
30
00.
000

Tak więc wynik uzyskany w II itaracji świadczy o tym, że proces iteracyjny może ograniczyć się do dwóch iteracji, ponieważ wynik jest prawidłowy.

Zadanie do wykonania:

Przeliczyć moment: 12
00
00.
000 + nr grupy 30
+ nr na liście 10
czasu wschodnioeuropejskiego (polski czas letni) na czas gwiazdowy i odwrotnie oraz na czas słoneczny prawdziwy Greenwich i odwrotnie. Data i rok dowolne.

Ćwiczenie nr 4

Redukcje współrzędnych gwiazd

(od miejsc średnich do miejsc pozornych - widomych)

Redukcję wykonujemy w celu obliczenia współrzędnych widomych (pozornych) w konkretnym zadanym momencie mając współrzędne średnie podane na początek roku Rocznika Astronomicznego.

Praktyczne wzory to wzory Bessela wg koncepcji Atkinsona:

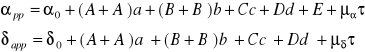
gdzie:

- współrzędne średnie na początek epoki,

A,B,E - współczynniki służące obliczeniu wpływu precesji i długookresowych

wyrazów nutacji,

C,D - współczynniki służące obliczeniu wpływu aberracji,

A',B' - współczynniki służące obliczeniu wpływu krótkookresowych wyrazów nutacji,

- roczny ruch gwiazdy w rektascenzji i deklinacji,

- ułamek dziesiętny roku (od początku do momentu obserwacji).

Współczynniki a, b, c, d, a', b', c', d', będące funkcjami współrzędnych średnich
oblicza się ze wzorów:

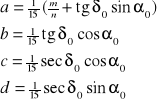
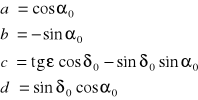
przy czym m i n to roczna precesja w rektascenzji i roczna precesja w deklinacji a
to średnie roczne nachylenie ekliptyki (wszystkie dane podane są w Roczniku Astronomicznym).

Ćwiczenie nr 5

Obliczenie wpływu refrakcji astronomicznej

Astronomiczne pomiary kierunków są skażone błędem refrakcji astronomicznej.

Z

G^'

∗

z^' r

Ziemia

warstwy atmosfery

r - kąt refrakcji,

z^' - odległość zenitalna obserwowana,

r = 60.^''3 · tg z^'

Jest to wzór przybliżony. Jest słuszny przy standardowych warunkach atmosferycznych, tzn. ciśnieniu równym 760 mm Hg i temperaturze t=0⁰. Można go używać ze skończoną dokładnością:

jako ścisły: dla z^' < 45⁰,

jako przybliżony dla: 45⁰ < z^' < 70⁰,

jeżeli z^' < 70⁰, wzoru nie należy stosować.

Dla przykładu:

- dla z^'= 45⁰ r = 0.^''02 ~ 0.^''03,

- dla z^' = 60⁰ r = 0.^''3,

- dla z^' = 70⁰ r = 1.^''27,

- dla z^' = 80⁰ r = 11^'',

- dla z^' = 90⁰ r = 36.^'6 (refrakcja w horyzoncie).

Można posługiwać się również nieco dokładniejszym wzorem, uwzględniającym wpływ ciśnienia i temperatury w miejscu pomiaru:

,

gdzie H i t to ciśnienie i temperatura w miejscu pomiaru.

W celu dokładnego obliczenia wpływu refrakcji astronomicznej, posługujemy się tablicami, ułożonymi przez Radau. Tablice te są podane w Roczniku Astronomicznym (RA).

Ogólny wzór refrakcji Radau jest następujący:

,

przy czym:

R₁ = R₀ + R₀· A · α · γ, - refrakcja normalna, poprawiona o wpływ temperatury,

A - zależy od temperatury t; przy t = 0⁰ ma wartość 0,

B - zależy od ciśnienia atmosferycznego; przy p = 760 mm Hg ma wartość 0,

α - jest funkcją z^'; przy z^' = 45⁰ ma wartość 1,

β - jest funkcją R₁; przy R₁ = 0^' ma wartość 1,

γ - jest funkcją temperatury t i odległości zenitalnej z^'.

W praktyce spotykamy się z trzema wariantami posługiwania się wzorem Radau:

dla z^' > 80⁰ stosujemy wzór rozwinięty:

R = R₁ + R₁ · B · β

gdzie R₁ = R₀ + R₀ · A · α · γ

dla 60⁰ < z^' < 80⁰ stosujemy wzór uproszczony:

R = R₁ + R₁ · B

gdzie R₁ = R₀ + R₀ · A · α

dla z^' < 60⁰

R = R₁ + R₁ · B

gdzie R₁ = R₀ + R₀ · A.

Zadanie: oblicz wpływ refrakcji (posługując się zarówno wzorami uproszczonymi jak i wzorami Radau) dla pomiaru odległości zenitalnych, równych:

z₁^' = 80⁰ 10^' 10.^''0 + n · 5^' + nr grupy ·10^',

z₂^' = 70⁰ 10^' 10.^''0 + n · 10^''+ nr grupy ·10^',

z₃^' = 30⁰ 10^' 10.^''0 + n · 15^''+ nr grupy ·10^'.

Obliczenia przeprowadź w tabelce, posługując się następującym przykładem:

z^'	T [^0]	H [mm]	A	α	γ	(1+Aαγ)	R0
44^009^'18^''=44.^016	+ 19.^08	763.2	-0.0707	1.000	1.00000	0.92930	0^'58.^''3 =58.^''3
73 45 42 =73.76	- 4.2	748.5	+0.0163	1.015	1.00000	1.01654	3 23.8 = 203.8
81 12 38 = 81.21	+ 10.9	752.5	-0.0401	1.047	0.99952	0.95804	6 12.8 = 372.8

R1	B	β	(1+Bβ)	R	Z
54.^''2 = 0^'.90	+0.0042	1.000	1.00420	54.^''4	44^010^'12^''
207.2 = 3.45	-0.0152	1.002	0.98477	204.0	73 49 06
357.2 = 5.95	-0.0098	1.004	0.99016	353.7	81 18 32

Ćwiczenie nr 6

Wyznaczenie azymutu z obserwacji Biegunowej

Wykonano pomiar kątów poziomych gwiazdy Biegunowej teodolitem Theo 010 Zeissa nr 148659. Pomiar wykonano w 12 seriach w dniu 5 września 1989 r.

Szerokość geograficzna miejsca obserwacji (na podstawie mapy): ၪ = 53^o08^', przewaga libelli nasadkowej = 34.2^cc; poprawka chronometru morskiego (Kirow nr 8579) =

5.IX.1989 20^h00^m00^s (T_wsch.-eur.) = -2.0^s

6.IX.1989 1^h00^m00^s (T_wsch.-eur.) = -4.0^s.

L.p.	Cel	Hz	Czas Tws.-eur	Libella nasadkowa	V (z)
1	L†	226-29-10.4	-	-
2	L†	226-29-19.8	-	-
3	L†	226-29-35.4	-	-
4	L†	226-29-30.6	-	-
5	L†	226-29-07.0	-	-
6	L†	226-29-23.6	-	-
7	L†	226-29-08.0	-	-
8	L†	226-29-20.0	-	-
9	L†	226-29-13.6	-	-
10	L†	226-29-15.2	-	-
11	L†	226-29-13.0	-	-
12	L†	226-29-12.8	-	-
13	L	29-13-79,77,77,66,64	22^h03^m17^s	l1=5, p1=41 l2=47, p2=12	34^o.16
14	L	29-13-72,72,69,72,74	22^h06^m35^s
15	L	29-13-38,38,36,30,32	22^h14^m27^s
16	L	29-13-22,15,22,14,18	22^h19^m55^s
17	L	29-12-78,87,68,66,66	22^h25^m10^s
18	L	29-12-54,58,52,54,50	22^h27^m32^s
19	L	29-12-40,32,34,38,38	22^h31^m47^s
20	L	29-11-66,65,60,55,56	22^h39^m22^s
21	L	29-10-94,92,86,88,94	22^h42^m44^s
22	L	29-10-49,44,45,53,53	22^h49^m17^s
23	L	29-10-04,12,02,10,02	22^h51^m34^s
24	L	29-09-45,51,47,53,48	22^h53^m07^s

L.p.	Cel	Hz [grady]	Czas Tws.-eur	Libella nasadkowa	V (z)
25	P†	26-28-08,04,12,10,12	-	-
26	P†	26-28-13,16,16,12,15	-	-
27	P†	26-28-00,04,06,00,00	-	-
28	P†	26-28-14,10,08,10,05	-	-
29	P†	26-28-14,10,10,14,11	-	-
30	P†	26-28-08,12,14,15,09	-	-
31	P†	26-28-12,08,14,12,06	-	-
32	P†	26-28-15,18,22,18,15	-	-
33	P†	26-28-14,13,16,15,18	-	-
34	P†	26-28-06,10,10,08,15	-	-
35	P†	26-28-14,10,12,10,10	-	-
36	P†	26-28-12,20,22,16,14	-	-
37	P	229-08-30,34,28,22,31	22^h56^m24^s	l1=8, p1=45 l2=49, p2=13	36^o.54
38	P	229-08-09,13,12,27,16	22^h58^m22^s
39	P	229-07-42,28,36,30,34	23^h01^m29^s
40	P	229-07-00,02,09,95^*,11	23^h04^m19^s
41	P	229-06-32,32,30,22,20	23^h08^m00^s
42	P	229-06-11,06,04,00,04	23^h10^m14^s
43	P	229-05-67,54,60,54,60	23^h12^m48^s
44	P	229-05-46,30,37,42,45	23^h13^m58^s
45	P	229-05-01,94^*,98^*,92^*,02	23^h15^m53^s
46	P	229-04-50,52,55,55,53	23^h17^m12^s
47	P	229-04-37,27,34,34,32	23^h21^m45^s
48	P	229-03-96,90,96,86,88	23^h24^m11^s

Wzory użyte w obliczeniach:

b - wielkość nachylenia poziomej osi obrotu lunety teodolitu, obliczana na podstawie wskazań libelli nasadkowej

၄Hz - wpływ nachylenia na odczyt koła poziomego,

a^N_* - azymut gwiazdy Biegunowej obliczany w momencie pomiaru

c^* - kolimacja kierunku do gwiazdy; c - kolimacja kierunku poziomego (do celu ziemskiego)

Uwaga! Obliczenia należy przeprowadzić, przyjmując czas pomiaru powiększony o nr z listy razy 5 minut oraz pełną serię według ustalonego schematu.

17

---