1. Proszę omówić budowę neuronu biologicznego

Komórka neuronowa poprzez swoje dendryty odbiera sygnały elektryczne pochodzące od synaps (końcówki transmitujące impulsy) innych komórek. Sygnały mogą być pobudzające i hamujące. Jeżeli potencjał elektryczny ma odpowiednią wartość (jest wystarczająco ważny), komórka sama generuje sygnał elektryczny i poprzez własne synapsy przekazuje go innym neuronom. W ludzkim mózgu jest ok. 10 ^ 11 neuronów i ok. 10 ^15 połączeń.

2. Proszę przedstawić model neuronu McCullocha-Pittsa

Sygnały wej x_i, gdzie i= 1, 2,...,n, mają wartość 1 lub 0, zależnie od tego, czy w chwili k impuls wej pojawił się,, czy nie. Sygnał wyj.- y. Reguła aktywacji neuronu :

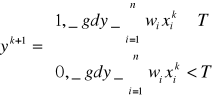
k= 0,1,2,... oznacza kolejne momenty czasu,

Wi multiplikatywną wagą przypisaną połączenia wej i z błoną neuronu. pomiędzy chwilami k oraz k +1 upływa jednostkowy czas opóźnienia, ze Wi=+1 dla synaps pobudzających, a Wi =-1 dla synaps hamujących oraz T jest wartością progową poniżej której neuron nie zadziała.

Przy dobrym doborze wag i progów można zrealizować funkcje logiczne NOT, OR AND NOR lub NAND, Przykłady realizacji trójwejściowych bramek NOR i NAND za pomocą, modelu neuronu McCullocha Pittsa

NOR

NAND

Model ten jest punktem wyjścia do konstrukcji najprostszej jednokierunkowej sieci neuronowej o nazwie perceptron. Model ten powstał w 1943 roku. Jako funkcję progową w tym modelu przyjmuje się funkcje jednostkową f(x)={1 dla x >=0 ; 0 dla x< 0}, funkcję bipolarną f(x)={1 dla x >=0 ; -1 dla x< 0} .Obecnie wykorzystuje się funkcje sigmoidalne f(x) = 1/1+e^-Bx gdzie b > 0, lub tangens hiperboliczny f(x)= tgh(ax/2) a>0. Pozwala to podzielić N-wymiarową płaszczyznę wektorów wejściowych na dwie półpłaszczyzny. Tzn. zakwalifikować sygnał wejściowy do jednej z dwóch grup.

4. Proszę wyjaśnić bezcelowość tworzenia wielowarstwowych liniowych sieci

Stosując liniowe sieci neuronowe nie uzyskamy korzyści z budowy sieci wielowarstwowej,

bo będzie miała takie same właściwości jak sieć jednowarstwowa. Jeżeli odwzorowanie dla

sieci jednowarstwowej zapiszemy w postaci Y = Wk * X gdzie Wn jest macierzą wag neuronu, a X jest wektorem sygnałów wejściowych. A następnie wynik tego odwzorowania wprowadzimy na drugą warstwę neuronów U=Wm*Y co w wyniku daje --> U=Wk*Wm*X stosując rachunek macierzowy otrzymamy U= Wkm *X gdzie Wkm jest iloczynem wektorowym oznacza to że związek pomiędzy U a X jest nadal odwzorowaniem liniowym niczym istotnym nie różniącym się od odwzorowania dla sieci jednowarstwowej.

5. Proszę narysować jednokierunkową jednowarstwową sieć neuronową o binarnych funkcjach aktywacji, mając następujące dane:

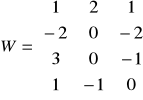
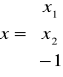
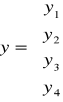
6. Proszę wyjaśnić na czym polega uczenie z nauczycielem i bez nauczyciela.

UCZENIE Z NAUCZYCIELEM

Uczenie z nadzorem lub inaczej - z nauczycielem zwane również uczeniem metodą wstecznej propagacji błędów pokazuje iż pierwszą czynnością w procesie uczenia jest przygotowanie dwóch ciągów danych:

- uczącego

- weryfikującego.

Ciąg uczący jest to zbiór danych, które charakteryzują dany problem. Jednorazowa porcja danych nazywana jest wektorem uczącym. W jego skład wchodzi wektor wejściowy czyli te dane wejściowe, które podawane są na wejścia sieci i wektor wyjściowy czyli takie dane oczekiwane, jakie sieć powinna wygenerować na swoich wyjściach. Po przetworzeniu wektora wejściowego, nauczyciel porównuje wartości otrzymane z wartościami oczekiwanymi i informuje sieć czy odpowiedź jest poprawna, a jeżeli nie, to jaki powstał błąd odpowiedzi. Błąd ten jest następnie propagowany do sieci ale w odwrotnej niż wektor wejściowy kolejności (od warstwy wyjściowej do wejściowej) i na jego podstawie następuje taka korekcja wag w każdym neuronie, aby ponowne przetworzenie tego samego wektora wejściowego spowodowało zmniejszenie błędu odpowiedzi. Procedurę taką powtarza się do momentu wygenerowania przez sieć błędu mniejszego niż założony. Wtedy na wejście sieci podaje się kolejny wektor wejściowy i powtarza te czynności. Po przetworzeniu całego ciągu uczącego (proces ten nazywany jest epoką) oblicza się błąd dla epoki i cały cykl powtarzany jest do momentu, aż błąd ten spadnie poniżej dopuszczalnego. Jeżeli mamy już nauczoną sieć, musimy zweryfikować jej działanie. . Do tego używamy ciągu weryfikującego, który ma te same cechy co ciąg uczący tzn. dane dokładnie charakteryzują problem i znamy dokładne odpowiedzi. . Dokonujemy zatem prezentacji ciągu weryfikującego z tą różnicą, że w tym procesie nie rzutujemy błędów wstecz a jedynie rejestrujemy ilość odpowiedzi poprawnych i na tej podstawie orzekamy, czy sieć spełnia nasze wymagania czyli jak została nauczona.

UCZENIE BEZ NAUCZYCIELA.

Sieci neuronowe mogą być uczone bez udziału nauczyciela za pomocą metody hebbian learning.

Zasada polega na tym, że waga w_i^(m) i- tego wejścia m- tego neuronu wzrasta podczas prezentacji j-tego wektora wejściowego X^(j) proporcjonalnie do iloczynu i-tej składowej sygnału wejściowego x_i^(j) docierającego do rozważanej synapsy i sygnału wyjściowego y_m^(j) rozważanego neuronu. Zapisując to wzorem, otrzymujemy:

, przy czym

indeksy oznaczają:

1. numer składowej części wektora wejściowego,

10. numer kolejny pokazu (prezentacji) wektora wejściowego

m- numer kolejny neuronu

Tak więc np. wzmocnieniu podlegają te wagi, które, które są aktywne (wartość x_i^(j) jest duża) w sytuacji, gdy „ich” neuron jest aktywny (wartość y_m^(j) jest duża).

Inaczej mówiąc, jeżeli przy pierwszej prezentacji któryś z neuronów zasygnalizuje pewne pobudzenie, to w miarę zwiększania ilości prezentacji sygnalizacja przez ten właśnie neuron będzie coraz wyraźniejsza.

Tego typu sieć potrafi grupować przychodzące bodźce w kategorie, ponieważ neuron wytrenowany dla określonego sygnału X, potrafi również rozpoznać sygnały podobne do niego.

Uczenie z nauczycielem i bez nauczyciela

Z nauczycielem

przy nowych danych wej nauczyciel podpowiada pożądaną| odpowiedz d odległość p(d,y) pomiędzy rzeczywistą a pożądaną odpowiedzią sieci jest miarą błędu używana do korekcji parametr6w sieci. Zestaw obrazów wej i wyj w czasie nauki nazywamy zbiorem uczącym jest realizacją procesu przypadkowego i procedura minimalizacji błędu musi uwzględnić jego własności statystyczne

Bez nauczyciela

sieć musi się uczyć poprzez analizę reakcji na pobudzenia. Samo uczenie może doprowadzić do znalezienia granic pomiędzy klasami obrazów wej rozmieszczonych w skupiskach lub bez. .Regułą adaptacji jest zasada, ze obraz dodawany jest do tego skupiska-do centrum którego leży najbliżej.

7. Proszę opisać koncepcję przyrostowego samouczenia.

Przyrostowe samouczenie polega na uzależnieniu procesu zmiany wag od przyrostów sygnałów wejściowych na synapsie i wyjściowych, na danym neuronie:

w_i­^(m)(j+1)= w_i­^(m)(j)+η[(x_i^(j)- x_i^(j-1))( y_m­^(j)- y_m­^(j-1))]

W niektórych wypadkach ta przyrostowa strategia daje znacznie lepsze rezultaty niż „czysty” algorytm Hebba.

8. Proszę wyjaśnić uczenie metodą Hebba

Jeżeli akson komórki A bierze systematycznie udział w pobudzaniu komórki B powodującym jej aktywację, to wywołuje to zmianę metaboliczną w jednej lub obu komórkach, prowadzącą do wzrostu skuteczności pobudzaniu B przez A.

Dodatnia wartość składnika korelacyjnego y_ix_j powoduje wzrost wagi wij, i silniejszą reakcję neuronu. Nieraz trzeba przeciwdziałać nieograniczonemu wzrostowi wartości wag, gdy składnik y_ix_j ma ciągle ten sam znak

Syg uczący to syg wuj neuronu:

r = y_i = f(w_i^t x)

przyrost wektora wagi:

każda w_ij zmienia się o:

Δw_ij = cy_ix_j, j=1,2,......n

warunek: ustawienia wag na wartości przypadkowe z otoczenia w_i = 0

Reguła Hebba polega na tym, że waga w_i^(m), i-tego wejścia m-tego neuronu wzrasta podczas prezentacji j-tego wektora wejściowego X^(j) proporcjonalnie do iloczynu i-tej składowej sygnału wejściowego x_i^(j) docierającego do rozważanej synapsy i sygnału wyjściowego y_m^(j) rozważanego neuronu. Krótko mówiąc: algorytm modyfikowania wag opiera się na wzorze:

w_i­^(m)(j+1)= w_i­^(m)(j)+ηx_i^(j) y_m­^(j)

przy czym neuron może być określony jako element liniowy:

y_m­^(j)=Σⁿ_i=1 w_i­^(m)(j) w_i­^(j)

Podwójne górne indeksy przy współczynnikach wagi w_i­^(m)(j) wynikają z faktu, że trzeba uwzględnić numerację neuronów, do których wagi te należą (m) oraz numerację kroków, wynikających z kolejnych pokazów.

9. Proszę omówić perceptronową regułę uczenia

Reguła perceptronowa dotyczy nauki z nauczycielem.

Sygnał uczący jest różnicą między odpowiedzią pożądaną a rzeczywistą (Rosenblatt ,1958)

_def

r = d_i - y_i

gdzie y_i = sgn(w_i^t x)

Korekcja wag odbywa się wg zależności

Δw_i = c[d_i - sgn(w_i^t x)]x

Jak widać reguła ta odnosi się do sieci z neuronami dyskretnymi, a w równaniu założono dodatkowo, że funkcja aktywacji jest bipolarna. Korekcja wag jest przeprowadzana tylko wtedy , gdy odwzorowanie dokonane przez neuron jest błędne , przy czym wartość błędu jest wbudowana w regułę uczenia. Oczywiście skoro pożądana odpowiedź jest równa albo 1,albo -1 algorytm dostrajania wag Δw_i = c[d_i - sgn(w_i^t x)]x redukuje się do wzoru:

Δw_i = ⁺_- 2cx

Gdzie znak + (plus) obowiązuje, gdy d_i = 1 , y_i = -1, znak - (minus) ,gdy jest odwrotnie.

Jak wspomniano wyżej , dla d_i = y_i wagi pozostają bez zmian. Początkowe wartości wag mogą być dowolne.

10. Proszę omówić regułę uczenia delta

Rozpatrzymy sieć składającą się z K ciągłych neuronów:

Dla oznaczeń jak na rysunku sygnał wyjściowy wynosi

Z=Γ[Wy]

Gdzie

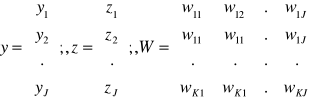
Γ jest nieliniowym operatorem o postaci

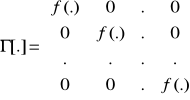
Błąd klasyfikacji jednego obrazu wyjściowego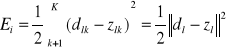

Gdzie d_l i z_l oznaczają odpowiednio pożądane i aktualne sygnały wyjściowe gdy na wejście podano obraz y_l.

Do wyznaczenia wartości wag minimalizujących błąd E_l zastosujemy metodę gradientową. Załóżmy, że y_J=const=-1 zarówno w fazie uczenia, jak i w fazie działania sieci oraz że wagi w_kJ dla k=1,2,..,K są w czasie uczenia traktowane tak samo jak pozostałe . Przyjmując zasadę korekcji wag otrzymujemy:

Stosując wzór na pochodne cząstkowe możemy napisać

Pochodna błędu po wielkości net nazywa się sygnałem błędu delta generowanym przez k-ty neuron i jest zdefiniowana następująco:

ponieważ

więc w_kj=w_kj+ηδ_zky_j k=1,2,..k j=1,2,..,J

lub stosując zapis macierzowy

W^t=W+ηδ_zy^t, gdzie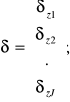
Obliczymy teraz wartość δ^zk:

i ostatecznie

Podstawiając otrzymane wyrażenie do równania otrzymamy w_kj'=w_kj+η(d_k-z_k)f'(net_k)y_j

Dla unipolarnej funkcji aktywacji f(net)

δ_zk=(d_k-z_k)z_k(1-z_k)

Podobnie dla bipolarnej funkcji aktywacji f(net mamy:

δ_zk=(d_k-z_k)(1-z_k²)

11. Proszę omówić regułę uczenia Widrowda-Hoffa.

Reguła Widrowd-Hoffa odnosi się do uczenia z nauczycielem sieci neuronowych o dowolnych funkcjach aktywacji, gdyż minimalizuje błąd średni kwadratowy (ang. least mean square = LMS) pomiędzy pożądaną odpowiedzią a pobudzeniem. Sygnał uczący jest zdefiniowany jako:

(2.32)

a korekta wag ma postać:

(2.33)

Reguła ta może być uważana za szczególny przypadek reguły delta. Istotnie, dla liniowej funkcji aktywacji jej pochodna jest stała i można ją wprowadzić do stałej uczenia. Ze względu na przyjęte kryterium minimalizacji reguła ta jest zwana też regułą LMS. Wagi początkowe mogą mieć dowolne wartości.

12. Uogólniona reguła delta

Obowiązuje dla neuronów z ciągłymi funkcjami aktywacji i nadzorowanego trybu uczenia. Sygnał uczący, zwany sygnałem delta, zdefiniowany jest jako:

, gdzie f' jest pochodną funkcji aktywacji. Reguła delta daje się łatwo wyprowadzić jako wynik minimalizacji kwadratowego kryterium błędu. Wzór na korekcję wag ma postać:

, gdzie c jest przyjętą arbitralnie stałą. Wartości początkowe wag mogą być dowolne.

Uwaga: indeksy powinny być na dole czyli x1=x₁

12. Proszę omówić uogólnioną regułę delta

Jest ona uogólniona na jednokierunkowe sieci warstwowe. Sygnał wyjściowy sieci dwuwarstwowej wynosi :

gdzie:

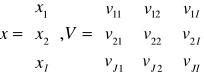
Jest to sieć dwuwarstwowa z neuronami ciągłymi.

Zakładamy że

x₁=-1, v_J1= v_J2=...= v_JI-1=0 v_JI=1

stąd wynika że y_J=-1

Otrzymujemy wzory:

gdzie j=1,2...J-1 i=1,2...I

oraz

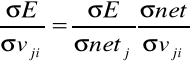
Sygnał błędu delta j-tego neuronu to:

ponieważ: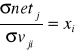
, i=1,2..I

otrzymujemy:

lub w postaci macierzowej:

gdzie: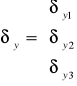

Wartość sygnału błędu
wyraża się wzorem:

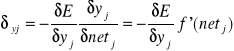
Po przekształceniach otrzymujemy:

, j=1,2...J-1

Otrzymujemy zasadę korekcji wag w warstwie ukrytej:

, j=1,2..J-1, i=1,2..I

Jest to uogólniona reguła delta. Wynika z niej że korekcja wag dochodzących do j-tego neuronu w warstwie ukrytej jest proporcjonalna do sumy ważonej wszystkie wartości δ w warstwie następnej.

Obowiązuje dla neuronów z ciągłymi funkcjami aktywacji i nadzorowanego trybu uczenia. Sygnał uczący, zwany sygnałem delta, zdefiniowany jest jako:

, gdzie f' jest pochodną funkcji aktywacji. Reguła delta daje się łatwo wyprowadzić jako wynik minimalizacji kwadratowego kryterium błędu. Wzór na korekcję wag ma postać:

, gdzie c jest przyjętą arbitralnie stałą. Wartości początkowe wag mogą być dowolne.

Uwaga: indeksy powinny być na dole czyli x1=x₁

13. Proszę omówić korelacyjną regułę uczenia

Przyjmując w ogólnej regule uczenia Δw_i (t)= cr[w_i(t),x(t), d_i (t)]x(t) r = d_i otrzymujemy regułę korelacyjną, w której korekta wektora wag ma postać Δw_i = cd_ix

Poprawka każdej składowej wektora wag jest tutaj proporcjonalna do iloczynu odpowiedniej składowej obrazu wejściowego i pożądanego przy tym wzorca wyjścia. Taka zasada uczenia czyni regułę korelacyjną szczególnie przydatną do zapamiętywania informacji w sieciach z neuronami binarnymi. Można też uważać tę regułę za odpowiednik reguły Hebba dla nauki z nauczycielem. Z porównania wzorów Δw_i = cd_ix i Δw_i = cy_ix widać, że rolę sygnału rzeczywistego y_i z metody Hebba odgrywa tu sygnał pożądany d_i. Podczas nauki metodą korelacyjną przyjmuje się zerowe wartości początkowe wag.

14. Proszę omówić regułę uczenia WTA.

W odróżnieniu od uczenia Hebba w uczeniu konkurencyjnym tylko jeden neuron może być aktywny (przyjmuje na wyjściu stan 1), a pozostałe pozostają w stanie spoczynkowym(stan 0) - uczenie typu WTA Winner Takes All. Grupa neuronów współzawodniczących otrzymuje te same sygnały wejściowe x_j. W zależności od aktualnych wartości wag sygnały wyjściowe neuronów u_j =ΣW_ij x_j różnią się między sobą. W wyniku porównania tych sygnałów zwycięża ten neuron, którego wartość u_j jest największa (jego wektor wag jest najbliższy aktualnemu wektorowi uczącemu x). Neuron przyjmuje stan 1, co umożliwia mu aktualizację wag W_ij dochodzących do niego według wzoru W_ij( k+1)= W_ij( k)+η[x_j - W_ij( k)]. Tak następuje adaptacja jego wag do danego wektora x. Przy podawaniu wielu wektorów zbliżonych do siebie będzie zwyciężał ten sam neuron, pozostałe neurony dopiero w wyniku zwycięstwa przy następnej prezentacji wektora wejściowego będą miały szansę na aktualizacją wag i uczenie. W efekcie takiego współzawodnictwa następuje samoorganizacja procesu uczenia. Neurony dopasowują swoje wagi w ten sposób, że przy prezentacji grup wektorów wejściowych zbliżonych do siebie zwycięża zawsze ten sam neuron. W trybie odtworzeniowym, w którym przy ustalonych wartościach wag podaje się na wejście sieci sygnały testujące, neuron przez zwycięstwo we współzawodnictwie rozpoznaje swoją kategorię (zastosowania - klasyfikacja wektorów).

15. Omówić regułę uczenia „outstar”.

Reguła gwiazdy wyjść (outstar) używa się jej do uczenia powtarzających się, charakterystycznych właściwości relacji wejście - wyjście. Wprawdzie uczenie odbywa się z nauczycielem, ale od sieci oczekuje się dodatkowo zdolności wydobywania statystycznych własności sygnałów wejściowych i wyjściowych. Korektę wag oblicza się jako *w_j = β(d - w_j). W odróżnieniu od wszystkich pozostałych reguł uczenia dostrajane są wagi w połączeniach rozbiegających się z wyjścia neuronu, tzn. dostraja się wektor w_j = [w_1j w_2j ... w_pj ]^t .Współczynnik β jest niewielką, arbitralnie dobieraną liczbą dodatnią malejącą w trakcie uczenia. Uczenie metodą gwiazdy wyjść prowadzi do wytworzenia wymaganej reakcji na określony obraz wejściowy nawet w tedy gdy korzysta się z rzeczywistego, a nie pożądanego sygnału wyjściowego.

k=1

W koncepcji tej rozważa się wagi wszystkich neuronów całej warstwy, jednak wybiera się wyłącznie wagi łączące te neurony z pewnym ustalonym wejściem. W sieciach wielowarstwowych wejście to pochodzi od pewnego ustalonego neuronu wcześniejszej warstwy i to właśnie ten neuron staje się „gwiazdą wyjść” - outstar. Wzór opisujący uczenie sieci outstar jest następujący

w_i­^(m)(j+1)= w_i­^(m)(j)+η^(j)(y_m^(j)-w_i^(m)(j))

Warto raz jeszcze podkreślić odmienność powyższego wzoru w stosunku do poprzednio rozważanych. Tutaj i jest ustalone (arbitralnie lub w jakiś inny sposób),natomiast m jest zmienne i przebiega wszystkie możliwe wartości (m=1,2,....,k). Reguła zmieniania η^(j) jest w tym wypadku nieco inna, niż przy instar i może być dana wzorem:

η^(j)=1-λj

Metoda outstar znajduje zastosowanie przy uczeniu sieci wytwarzania określonego wzorca zachowań Y w odpowiedzi na określony sygnał inicjujący x_i.

16.Wyjaśnić na czym polega proces autoasocjacji.

Załóżmy, że sieć może zapamiętać pewien zbiór obrazów wzorcowych. Jeżeli takiej sieci zaprezentujemy obraz podobny do któregoś z zapamiętanych, to może ona te obrazy skojarzyć. Proces taki nazywamy autoasocjacją. Bodźcem do odtworzenia określonego wzorca jest zwykle jego zniekształcona wersja, jak to pokazano na rys. 2.16a.

obraz

wejściowy

autoasocjacja

niekompletny

kwadrat

kwadrat

Rys 216. Odpowiedz przez kojarzenie a) autoasocjacja

17. Wyjaśnić na czym polega proces heteroasocjacji.

Hetero asocjacja - kojarzenie obrazów wej (kojarzone są pary obrazów, i nawet zniekształcony obraz wej może wywołać właściwą hetero asocjację na wyj

18. Proszę przedstawić schemat blokowy klasyfikatora obrazów należących do R klas.(str. 77)

1

2

x i

R kategoria

Dyskryminatory

Jednowarstwowa sieć dyskretna klasyfikująca obrazy należące do wielu klas

Istnieją dwa sposoby sygnalizowania kategorii obrazu przez klasyfikatory. Przy tak zwanej reprezentacji lokalnej układ sygnalizuje klasę i₀ poprzez wartość 1 na wyjściu i-tego neuronu i wartości -1 na wyjściach pozostałych neuronów czyli

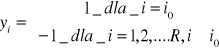
-Reprezentacja lokalna- układa sygnalizację klas

-Reprezentacja rozproszona binarna - numer klasy jest kodowany za pomocą dowolnej kombinacji sygnałów -1,1

19. Proszę wyjaśnić pojęcia: obszary i powierzchnie decyzyjne, funkcje dyskryminacyjne.(str.76)

klasyfikator obrazów odwzorowuje punkt w n- wymiarowej przestrzeni euklidesowej Eⁿ (zwanej przestrzenią obrazów) w liczby i_y=1,2,...,R; są one oznaczone odpowiednio

R₁,R_2,... ,R_R i są one nazywane obszarami decyzyjnymi. Są one oddzielone od siebie przez powierzchnie decyzyjne; w przypadku dwuwymiarowej przestrzeni obrazów Eⁿ powierzchniami decyzyjnymi są linie na płaszczyźnie; w przypadku ogólnym w przestrzeni Eⁿ powierzchniami decyzyjnymi są (n-1)- wymiarowe hiperpowierzchnie.

Funkcje dyskryminacyjne g_i(x) obliczane są na podstawie danego obrazu wejściowego x; mają tę własność że dla wszystkich x należących do kategorii i

g_i(x)> g_j(x), i,j=1,2,...,R i ≠j

Tak więc wewnątrz obszaru R_i i-ta funkcja dyskryminacyjna przyjmuje wartość największą.

Funkcje dyskryminacyjne g_i(x) i g_j(x) dla przylegających obszarow decyzyjnych R_i, R_j definiują powierzchnię decyzyjną pomiędzy tymi obszarami w przestrzeni Eⁿ. Z własności funkcji dyskryminacyjnych bezpośrednio wynika, że równanie powierzchni decyzyjnej pomiędzy obszarami decyzyjnymi R_i i R_j ma postać

g_i(x)- g_j(x)=0

20. Proszę wyjaśnić na czym polega koncepcja uczenia parametrycznego.

Parametryczny - dwuetapowe (metody klasyfikacyjne), polegające na znajdowaniu wartości pewnych nieznanych wartości, następnie na wyznaczeniu na drodze analitycznej na drodze wag

21. Proszę wyjaśnić pojęcie klasyfikatora minimalno-odległościowego.

Klasyfikator mmimalnoodległościowy, klasyfikujący obrazy do R kategorii. Mamy R punktów prototypowych P₁,P₂,... ,P_R, każdy reprezentuje inną klasę. Odległość euklidesowa pomiędzy punktem x a P_i to:

Obraz x zostaje zaliczony do klasy, który odpowiada najbliższemu P_i. Kwadrat odległości między x a P_i

Funkcja dyskryminująca:

Widać, że fun dyskryminacyjne są liniowe. Przyrównując je do postaci funkcji liniowej:

otrzymujemy wagi: w_i=P_i

w_i,n+1 = -1/2 P_i^t P_i

i=1,..R

Klasyfikator minimalnoodiegłościowy realizujący liniowe funkcje dyskryminacyjne - maszyna liniowa składa się z R węzłów obliczających iloczyny skalarne i układu wybierającego max.

Powierzchnia decyzyjna pomiędzy przylegającymi obszarami decyzyjnymi R_i R_j staje się hiperpłaszczyzną:

Wektor rozszerzony:

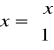
Funkcje można zapisać

g_i(x) = w_i^t x

i=1,..,R

22. Proszę wyznaczyć funkcje dyskryminacyjne dla maszyny liniowej, znając następujące punkty :

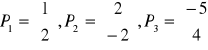
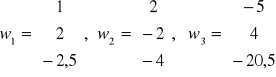
obliczamy funkcje dyskryminacyjne :

23.Proszę wyjaśnić pojęcie hiperpłaszczyzny obrazu.

Każdemu rozszerzonemu wektorowi obrazu x odpowiada w przestrzeni wag hiperpłaszczyzna

w^tx=0

nazywana ­­HIPERPŁASZCZYZNA OBRAZU.

Hiperpłaszczyzna obrazu przechodzi przez początek układu współrzędnych prostopadle do wektora x. Dzieli ona przestrzeń wag na dwie części. Do jednej zwanej stroną dodatnią należą punkty, dla których w^tx>0, do części drugiej zwanej stroną ujemną należą punkty dla których w^tx<0.

25. Wyjaśnić na czym polega reprezentacja lokalna klas obrazów.

Istnieją dwa sposoby sygnalizowania kategorii obrazu przez klasyfikatory. Przy tak zwanej reprezentacji lokalnej układ sygnalizuje klasę i₀ poprzez wartość 1 na wyjściu i-tego neuronu i wartość -1 na pozostałych neuronach, czyli

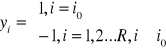
Reprezentacja lokalna wymaga przyjęcia liczby neuronów liczbie klas, natomiast przy reprezentacji rozproszonej liczba neuronów może być mniejsza. Reprezentacja lokalna, w przypadku sieci jednowarstwowych, wymaga, aby liniowo separowalne obszary decyzyjne miały odpowiedni kształt. Wymagane jest, aby każdy z tych obszarów można było odseparować hiperpłaszczyzną od pozostałych obszarów. Na przykład na to, aby sieć o reprezentacji lokalnej mogła klasyfikować na płaszczyźnie punkty, z których reprezentuje inną klasę, powinny się one znajdować na wierzchołkach wielokąta wypukłego; niemożliwe będzie na przykład użycie reprezentacji lokalnej do sygnalizacji czterech klas reprezentowanych przez punkty (1,1),(5,1),(3,3),(3,5). W przypadku reprezentacji binarnej wymagane jest przyjęcie kodowania realizowanego geometrycznie - niemożliwe będzie na przykład zastosowanie do czterech klas reprezentowanych przez punkty (2,2),(2,4),(4,2),(4,4) reprezentacji odpowiednio 01, 00, 10, 11. Realizowaną reprezentacją otrzymamy przyporządkowując np. punktowi (2,2) sygnały 00, a punktowi (2,4) sygnały 00, a punktowi (2,4) sygnały 01.

26. Proszę podać przykład obrazów liniowo separowalnych i liniowo nie separowalnych

• przykład obrazów liniowo nie separowalnych

Żądamy aby klasyfikator realizował funkcję XOR

( wartość-1 na wyjściu punktom [0 0] i [1 1] na wejściu i wartość 1 punktom [0 1] i [1 0] )

Schemat klasyfikatora

Arbitralnie ustalony podział

-2x₁ + x₂ - ½ = 0 x₁ - x₂ - ½ = 0

Jednostkowe wektory normalne

r₁ = 1 [ -2 ] r₂ = 1 [ 1 ]

√5 1 √2 -1

y₁ = sgn(-2x₁ + x₂ - ½ ) y₂ = sgn(x₁ - x₂ - ½)

Odwzorowanie realizowane przez dwie pierwsze warstwy klasyfikatora

Obraz	Współrzędne w przestrzeni obrazów x1 x2	Współrzędne w przestrzeni odwzorowań y1 y2	Współrzędne w przestrzeni wyjść z	Numer klasy
A B C	0 0 0 1 1 0	-1 -1 1 -1 -1 1	-1 1 1	2 1 1
D	1 1	-1 -1	-1	2

Arbitralnie wybrana linia decyzyjna

y₁ + y₂ +1=0

z= sgn(y₁ + y₂ +1)

• przykład obrazów liniowo separowalnych

Zbiór uczący

x₁=1 x₃=3 -klasa 1

x₂=-0.5 x₄=-2 -klasa 2

Dla bipolarnej funkcji aktywacji

1 2

E_k= 2 [ d^k - [ 1 + exp(-net^k) -1]]²

2

E₁ (w)= [ 1 + exp(w₁ + w₂) ]²

2

E₂ (w)= [ 1 + exp(0.5w₁ + w₂) ]²

2

E₃ (w)= [ 1 + exp(3w₁ + w₂) ]²

2

E₄ (w)= [ 1 + exp(2w₁ + w₂) ]²

27. Proszę przedstawić algorytm wstecznej propagacji błędu dla sieci dwuwarstwowej

Dane jest p par uczących

{x₁,d_1,x_2,d_2,...,x_p,d_p},

gdzie x_i ma rozmiar I x 1,d_i ma rozmiar K x 1, a x_iI=-1, i=1,2,...,p. Wektor y_i o wymiarze (J x 1) jest wektorem wyjściowym warstwy ukrytej, a y_iJ=-1,i=1,2,..,p.

Wektor z o wymiarze K x 1 jest wektorem wyjściowym warstwy wyjściowej.

Parametr l oznacz numer kroku wewnątrz cyklu uczenia.

KROK 1: Wybór
0, E_max> 0.

KROK 2:Wybór elementów macierzy wag W i V jako niewielkich liczb losowych. Macierz W ma rozmiar K x J , macierz V ma rozmiar J x I.

KROK 3:Ustawienie wartości początkowych licznika kroków oraz zerowanie

błędu

l
1, E
0.

KROK 4:Podanie obrazu na wejście (obrazy mogą być też podawane w kolejno-

ści losowej) i obliczanie sygnału wyjściowego

x
x_l, d
d_l,

y_{i
f (V}
x), j=1,2,..., J-1,

gdzie v
jest j-ym wierszem V,

z_k
f (w
y), k=1,2,...,K,

gdzie w
jest k-tym wierszem W.

KROK 5: Uaktualnianie błędu

E
E+

-z_k)²

KROK 6:Obliczanie wektorów sygnałów błędów
i
obydwu warstw. Wek

tormaximum record size = 21 record size = 16777220
ma wymiar K x 1, a wektor
ma wymiar J x 1.Dla bipolarnej funkcji

aktywacji

=
(d_k-z_k)(1-z_k²), k=1,2,...,K,

=
(1-y_j²)

, j=1,2,...J-1.

Dla unipolarnej funkcji aktywacji

=(d_k-z_k)z_k(1-z_k), k=1,2,...,K,

=y_j(1-y_j)

, j=1,2,...,J-1.

KROK 7: Uaktualnianie wag warstwy wyjściowej

+
y_j , k=1,2,...,K j=1,2,...,J.

KROK8: Uaktualnianie wag warstwy ukrytej

+
x_i , j=1,2,...,J-1, i=1,2,...I.

KROK 9: Jeżeli l < p, to p
l+1 i przejście do kroku 4.

KROK 10: Cykl uczenia został zakończony. Jeżeli E<E _max, to zakończenie uczenia ; w przeciwnym razie rozpoczęcie nowego cyklu przez przejście do kroku 3.

28. Kryteria oceny sieci neuronowych o ciągłych i dyskretnych funkcjach aktywacji

odp. (krótka) błędy uczenia

odp. (długa)

Kryterium oceny sieci neuronów o ciągłych funkcjach aktywacji stanowią dwie def. błędu:

• Błąd łączny - suma błędów danych wyrażeniem:

po wszystkich „p” obrazkach uczących

Błąd ten opisuje zmiany jakości działania sieci w procesie uczenia.

• Znormalizowany błąd średni kwadratowy - do porównywania jakości działania sieci o różnej liczbie obrazów uczących lub różnej liczbie neuronów wyjściowych.

Kryterium oceny sieci neuronów z dyskretnymi funkcjami aktywacji jest:

• Błąd decyzji

gdzie N_b jest liczbą wyjść neuronów generujących błędne sygnały wyjściowe, zliczoną dla wszystkich obrazów uczących.

29. Proszę wyjaśnić przyrostowe i kumulacyjne uaktualnianie wag

W metodzie propagacji wstecznej oblicza się gradient błędu wyrażony wzorem:

gdzie d_l i z_l oznaczają odpowiednio pożądane i aktualne sygnały wyjściowe

i dokonuje się korekty wag każdorazowo po podaniu kolejnego wektora uczącego.

Takie postępowanie nosi nazwę PRZYROSTOWEGO UAKTUALNIANIA WAG.

Możliwe jest inne postępowanie w którym oblicza się gradient błędu łącznego danego wzorem

i dokonuje się korekty wag raz na jeden cykl tzn. po podaniu wszystkich obrazów uczących. Jest to wówczas KUMULACYJNE UAKTUALNIANIE WAG.

Efektywność obu metod jest zależna od rozwiązywanego problemu, ale uaktualnianie przyrostowe jest bardziej efektywne od kumulacyjnego.

Ponieważ gradient błędu łącznego jest sumą gradientów błędów dla poszczególnych obrazów kumulacyjne uaktualnianie wag można realizować obliczając poprawki wag po każdym obrazie uczącym, ale bez dokonywania ich zmiany. Zmiana wag jest dokonywana dopiero po całym cyklu znaczącym, czyli po podaniu wszystkich wzorców według reguły

Gdzie W_l jest wektorem korekcji wag po podaniu wektora uczącego

30.Proszę wyjaśnić, jak współczynnik nachylenia w sigmoidalnej, bipolarnej funkcji aktywacji wpływa na szybkość uczenia sieci

Funkcja aktywacji neuronu ƒ(net) charakteryzuje się współczynnikiem nachylenia λ. Pochodna funkcji aktywacji ƒ'(net), która stanowi współczynnik krotnościprzy wyznaczaniu sygnałów błędu &_z i &_y także jest zależna od λ. Tak więc zarówno wybór jak i kształt funkcji aktywacji ma duży wpływ na szybkość uczenia sieci.

Pochodna bipolarnej funkcji aktywacji (2.3a) względem zmiennej net

ƒ'(net) = 2 λexp(-λnet)

[1 + exp(-λnet)]²

Rys. 1 Pochodna funkcji aktywacji dla różnych wartości współczynnika λ

została przedstawiona na Rys.1 dla kilku wartości λ.Osiąga ona maksymalną wartość równą λ /2 dla net=0. Ponieważ wagi ustawione są proporcjonalnie do wartości ƒ'(net), najbardziej korygowane są wagi połączone z neuronami, na których wejściach łączny sygnał wejściowy net jest bliski zera, czyli wagi neuronów generujących sygnały wejściowe bliskie zera podlegają znacznie większej zmianie niż wagi neuronów znajdujących się w stanie nasycenia. Także transmitowane wstecz sygnały błędu są największe, gdy pochodzą od neuronów o pobudzeniach łącznych net bliskich zera.

Inną własnością wynikającą z rysunku jest to że przy ustalonym współczynniku korekcji η, wszystkie wagi korygowane są proporcjonalnie do współczynnika nachylenia λ. Wynika stąd, że wybór dużych wartości λ może prowadzić do podobnych rezultatów jak przyjęcie dużych wartości η . W związku z tym rozsądny jest wybór jakiejś standardowej wartości λ np. 1 , i wpływanie na szybkość zbieżności wyłącznie przez współczynnik η.

31. Proszę wyjaśnić i omówić metodę momentu.

dla
rozwiązanie równania różniczkowego jest następujące

zakładając że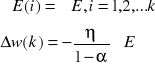
szczególny przypadek gdy wielkość gradientu jest stała

32. Proszę wyjaśnić pojęcia: sieci progowe, sieci interpolacyjne.

Schemat pamięci asocjacyjnej

Sieci progowe

gdzie
jest niewielkim błędem

Sieci interpolacyjne

gdzie
gdy

Pamięci adresowane zawartością :

• nie ma określonego umiejscowienia w pamięci

• adresowanie realizowane jest za pomocą poszukiwania sum oodległości...

33. Proszę krótko omówić asocjator liniowy.

Zadaniem pamięci asocjacyjnej jest przechowywanie p par wektorów {x⁽ⁱ⁾ ,y⁽ⁱ⁾ }, i=1,2,...,p. W pamięciach liniowych sygnał wyjściowy jest dany równaniem y=Wx, w którym x, y są wektorami o odpowiednio n i m składowych, a W jest macierzą o rozmiarach m x n . W ten sposób nieliniowe odwzorowanie zostało zredukowane do odwzorowania nieliniowego i dlatego pamięć nazywa się liniową. Ponieważ w odwzorowaniu nie występują nieliniowe funkcje aktywacji, więc czasami w celu uzyskania zgodności z ogólną postacią sieci neuronowej wprowadza się sztuczne funkcje aktywacji o postaci f(net)=net. Asocjator liniowy jest siecią interpolacyjną, a nie progową.

W asocjatorze liniowym należy zapamiętać pary wektorów {s⁽ⁱ⁾, f⁽ⁱ⁾}, i=1,2,...p , oznaczające odpowiednio wektory wejściowe i wyjściowe, gdzie: s⁽ⁱ⁾=[s⁽ⁱ⁾_{1 ,} s⁽ⁱ⁾₂ , ... s⁽ⁱ⁾_n] f⁽ⁱ⁾=[f⁽ⁱ⁾₁, f⁽ⁱ⁾₂ , ... ,f⁽ⁱ⁾_n] i=1,2, ... p.

Zaprojektowanie asocjatora liniowego sprowadza się do dobrania macierzy wag W we wzorze y=Wx w celu przekształcenia f⁽ⁱ⁾ - η⁽ⁱ⁾ = Ws⁽ⁱ⁾ i=1,2,...,p, zapewniającego możliwe dobre odwzorowanie wektorów s⁽ⁱ⁾ w wektory f⁽ⁱ⁾ ,czyli minimalizującego wyrażenie ∑_iη⁽ⁱ⁾. Wektor η⁽ⁱ⁾ nazywany jest przesłuchem wektorowym. Zadanie znalezienia optymalnej macierzy wag W jest rozwiązywane metodami regresji matematycznej. Do wyznaczenia macierzy W zastosujemy regułę Hebba. Dla tej reguły korekcja wagi pomiędzy i-tym węzłem wyjściowym i j-ym węzłem wejściowym wynosi w^'_ij=w_ij+f_is_i i=1,2, .. m j=1,2,...n (1) gdzie f_i i s_j są i-tą i j-tą składową wektorów f i s tworzących asocjację, a w_ij i w^;_ij oznaczają elementy macierzy wag przed korekcją i po niej. Zapisując wzór (1) w postaci macierzowej oraz wprowadzając wskaźniki oznaczające numer kroku iteracyjnego mamy W^k=W^k-1 + f^(k) s^(k)t gdzie f^(k) i s^(k) oznaczają k-te asocjacje. Przyjmując W⁰=0 i wykonując p kroków interacyjnych, otrzymujemy W=W^p=∑^p f^(k)s^{(k) t} (2) lub W=FS^t (3) gdzie F= [ f⁽¹⁾ f⁽²⁾ ... f^(p)],

k=1 def def

S=[s⁽¹⁾ s⁽²⁾ ... s^(p)]. p

Podstawiając wzór 1 i 2 i przyjmując że na wejście sieci podano wektor wzorcowy s^(j) otrzymujemy y=(∑ f^(k)

k=1

s^{(k) t}) s^(j) i następnie rozwiązując sumę mamy : y= f⁽¹⁾ s^{(1) t} s^(j) + ... + f^(j) s^{(j) t} s^(j) +...+ f^(p) s^{(p) t} s^(j) (4). Idealne odwzorowanie wymaga, aby y=f^(j) (5) . Porównując wzory 4 i 5 widać że warunkiem idealnego odwzorowania jest aby wzór wektorów {s⁽¹⁾ , s⁽²⁾ , ...,s^(p)} był układem ortonormalnym.

34. Proszę na rysunku przedstawić model sieci Hopfielda (wymienić zakładane ograniczenia dla wag)

W sieci tej neurony mają nieliniowe charakterystyki:

gdzie

a nieliniowość
dana jest prostą binarną funkcją

1 gdy

gdy

-1 gdy

• współczynniki wagowe
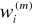
  łączące wyjście i - tego neurony z wejściem m - tego neuronu nie zależą od j. Wynika to z faktu, że rozważając sieć Hopfielda na tym etapie nie dyskutujemy problemu jej uczenia. Zakładamy, że wartości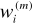
  zostały wcześniej ustalone za pomocą jakiegoś algorytmu (najczęściej przyjmuje się tu algorytm Hebba) i obecnie nie podlegają zmianom. Numer j oznacza natomiast chwilę czasową., określającą w jakim momencie procesu dynamicznego następującego po pobudzeniu sieci obecnie się znajdujemy. Po drugie sumowanie sygnałów wyjściowych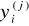
  z poszczególnych neuronów we wzorze definiującym łączne pobudzenie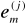
  odbywa się po wszystkich elementach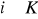
  czyli po wszystkich elementach sieci. Oznacza to, że w sieci przewidziane są także połączenia z warstw dalej położonych (wyjściowych) do warstw wcześniejszych - czyli sprzężenie zwrotne.

• macierz wag jest symetryczna tzn
  

.

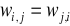
y₁ y₂ y_k

...

... ... ...

x₁ x₂ x_k

35. Proszę omówić algorytm asynchroniczny i synchroniczny przejścia stanów dla sieci Hopfielda.

Na rysunku 5.1 widoczna jest sieć neuronowa typu Hopfielda. Składa się ona z n neuronów z progami Ti, pobudzanych zarówno sygnałami zewnętrznymi, jak i sygnałami sprzężenia zwrotnego od innych neuronów, jak we wzorze poniżej:

i = 1, 2, . . . , y1,,

gdzie wektory wagowy i wyjściowy dane są jako

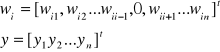
Definiując wektory: pobudzeń net, wejściowy x oraz progowy T analogicznie jak wektor wyjściowy, możemy opisać liniową część sieci z rys. 5.1 zależnością macierzową

net=Wy+x-T, gdzie

W modelu Hopfielda zakłada się, że macierz wag jest symetryczna, tzn. w_ij - w_ji, oraz, co widać na rys. 5.1, że wyjście dowolnego neuronu połą­czone jest poprzez multiplikatywne wagi z wejściami pozostałych neuronów, ale nie jest połączone z jego własnym wejściem.

Załóżmy chwilowo, że funkcja aktywacji jest funkcją signum, jak w ele­mencie PUL. Przejścia stanów będą zachodziły zgodnie z rekurencyjną za­leżnością

, k=1,2,3.... (5.3)

o której zakłada się, że ma charakter asynchroniczny, co tutaj oznacza, że w danej chwili ma miejsce aktualizacja tylko jednej spośród i = 1, 2, . . . , n składowych. Rekurencja zaczyna się od stanu y⁰ wymuszonego sygnałem inicjującym. W pierwszym kroku, dla k = 1, oblicza się y¹_i , przy czym wskaźnik i wybierany jest przypadkowo. Obliczenia dla pozostałych składowych, również wybieranych losowo, prowadzi się z wykorzystaniem składowych wektora y już zaktualizowanych w tym kroku, uzyskując ostatecznie y^l.

Posługując się równaniem macierzowym (5.2) można zapisać algorytm (5.3) w bardziej zwartej postaci:

, k = 1, 2, . . . (5.4)

Należy jednak zwrócić uwagę, że ta forma zapisu sugeruje zmianę algorytmu. Formalnie jest to teraz algorytm synchroniczny (równoległy), w którym wszystkie neurony warstwy mogą zmieniać swoje wyjścia równocześnie. Aby pozostać przy koncepcji asynchronicznej nalezy, każdy z kroków rekurencji rozbić na n indywidualnych przejść odbywających się w przypadkowej ko­lejności.

Dla ilustracji graficznej przedstawmy wektor wyjściowy w przestrzeni Eⁿ. Jest on tam reprezentowany przez jeden z wierzchołków n-wymiarowego hipersześcianu [-1,1]ⁿ. Podczas rekurencji (5.4), przebiegającej z założenia asynchronicznie, wektor y przesuwa się od wierzchołka do wierzchołka, aż wreszcie stabilizuje się w jednym z 2ⁿ możliwych wierzchołków. Stan koń­cowy y^k, gdy
, uzależniony jest od wag, progów, stanu początkowego i kolejności aktualizacji składowych y_i. Pojawia się przy tym szereg pytań: ile i jakie atraktory ma sieć? jakie są ich obszary przyciągania? jak osiągany jest stan równowagi? - czy wreszcie: jak należy zaprojektować sieć i obliczyć jej wagi, aby dokonywała wymaganych odwzorowań?

Dla oceny stabilności rozważanej sieci dynamicznej wprowadźmy tak zwaną funkcję energetyczną (zwaną też funkcją. stanu), dodatnią i ograni­czoną w przestrzeni wyjść. (Funkcji tej nie należy kojarzyć z fizycznym poję­ciem energii. Nazywamy ją tak ze względu na podobieństwo ich własności.) Jeżeli zmiany wartości funkcji energetycznej w trakcie wykonywania algo­rytmu (5.4) są niedodatnie, to można ją nazwać funkcją Lapunowa, a sieć jest asymptotycznie stabilna (Kaczorek, 1974).

W naszym przypadku funkcja energetyczna jest formą kwadratową

(5.5a)

Prześledźmy zmiany funkcji energetycznej w trakcie procesów przejścio­wydr. Niech w chwili k wyjście y; zmienia wartość o
y_i; (algorytm asyn­chroniczny). Gradient energii względem wektora wyjściowego, wynikający z (5.5a), ma postać

E=-1/2(W^t+W)y-x+T.

Przy symetrycznej macierzy W, dla której W^t = W, postać ta redukuje się do

E=-Wy-x+T.

Z uwagi na to, że tylko i-ta składowa gradientu jest niezerowa, uzyskujemy wzór na przyrost energii

E =(
E)^t
y = (-w^t_iy - x_i+ T_i)
y_i = -net_i
y_i. (5.6)

Z algorytmu aktualizacji (5.3) wynika, że zmiana y_i, o ile zachodzi, ma zawsze znak identyczny ze znakiem łącznego pobudzenia net_i, a więc iloczyn net_i
y_i jest zawsze nieujemny. Zmiana energii podczas aktualizacji wyjść jest zatem zawsze niedodatnia.

Aby minimalizacja funkcji energetycznej miała sens, trzeba jeszcze po­kazać, że funkcja ta ma minimum. Z własności form kwadratowych wynika, że funkcja (5.5), przy nieokreślonej z uwagi na zerowe elementy diagonalne macierzy W, nie ma w nieograniczonej przestrzeni wyjść ani minimum, ani maksimum. W rozważanym przypadku przestrzeń wyjść jest jednak ograniczona do wierzchołków w-wymiarowego sześcianu i stan przejściowy mnisi doprowadzić do punktu stabilnego, w którym energia (5.5) jest minimalna. Punkt ten jest granicznym rozwiązaniem równania (5.4), co zapisujemy jako

y^* = I'(Wy^* + x - T). (5.7)

Przypomnijmy, że spełnienie przez funkcję energetyczną (5.5) postulatu Lapunowa o niedodatniości przyrostów i wynikająca stąd stabilność rozwa­żanej sieci zostały wykazane przy założeniu, iż macierz wagowa jest symetryczna. Można też wykazać stabilność sieci z niesymetrycznymi wagami. Nie będziemy się nimi jednak zajmowali, gdyż ich własności są bardzo zbliżone do własności sieci symetrycznych, a te ostatnie łatwiej się projektuje. Dodatkowe założenie w_ii= 0 uzasadnimy w dalszej części tego rozdziału, przy rozpatrywaniu sieci z czasem ciągłym.

Inny przykład zbiegania się do startu równowagi przed­stawiony jest na rys. 5.2, gdzie mapa bitowa cyfry 4 złożona z 10 x 12 czarno-białych elementów jest aktualizowana według algorytmu (5.3). Ob­raz inicjujący jest zniekształcony przez zmianę wartości 20% przypadkowo wybranych elementów. Układ dochodzi do stanu stabilnego po czterech kro­kach; dla k , 5 żadne zmiany już nie zachodzą, gdyż sieć osiągnęła jeden ze stanów równowagi (5.7).

Stosowanie synchronicznego algorytmu aktualizacji może prowadzić do dwustanowego cyklu granicznego odpowiadającego obrazom komplementar­nym (Kamp i Hasler, 1990). Biorąc np. macierz wagową 2 x 2 o zerowych elementach diagonalnych, a pozostałych równych -1 i startując od wektora początkowego y⁰ =[-1 -l]^t z zerowymi wektorami x i T, otrzymujemy w pierwszym kroku

czyli ponownie wektor początkowy. Cykl graniczny składa się więc z komplementarnych stanów równowagi z którymi związana jest jednakowa energia. Zauważmy dla porównania ze w tych samych warunkach układ asynchroniczny przechodzi w pierwszym kroku do stabilnego stanu y¹=[1 -1]^t lub y¹=[-1 1]^t zależnie od kolejności aktualizacji składowych.

36.Proszę napisać i omówić funkcję energetyczną dla sieci Hopfielda

Służy ona do oceny stabilności rozważanej sieci dynamicznej. Zwana jest również funkcją stanu. Funkcja energetyczna jest formą kwadratową:

lub w postaci rozwiniętej:

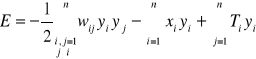
Gradient energii względem wektora wyjściowego ma postać:

Dla symetrycznej macierzy W wzór ma postać:

Z uwagi że tylko i-ta składowa gradientu jest niezerowa otrzymujemy wzór na przyrost energii:

Punkt będący ograniczonym rozwiązaniem zapisujemy jako:

Stosowanie synchronicznego algorytmu aktualizacji może prowadzić do dwustanowego cyklu granicznego odpowiadającego obrazom komplementarnym.

37. Proszę przedstawić algorytm zapisu i odczytu dla rekurencyjnej pamięci asocjacyjnej.

Algorytm zapisu i odczytu rekurencyjnej pamięci asocjacyjnej.

Danych jest p wektorów bipolarnych : {s⁽¹⁾, s⁽²⁾... s^(p)} gdzie:

s^(m)ma wymiar n x 1, m=1,2...p

początkowy wektor stanu v⁽⁰⁾ ma wymiar n x 1

Zapis:

Krok 1. podstawienie W←0 gdzie W ma wymiar n x n

Krok 2. dla m od 1 do p wykonanie W← s^(m) s^(m)t-I

Krok 3. zapis wektorów do pamięci jest zakończony

Odczyt:

Krok 1. ustawienie stanu początkowego v⁽⁰⁾=x

Krok 2. ustawienie liczb 1,2...n w losowej kolejności α₁, α₂... α_n

Krok 3. dla i od 1 do n wykonanie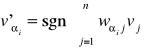

Krok 4. Jeśli v'_αi= v_αi , i=1,2...n to zakończenie procesu odczytu i uznanie sygnałów v'₁ , v'₂ ... v'_n za sygnały wyjściowe , w przeciwnym razie przejście do 2.

38. Sposoby obliczania pojemności autoasocjacyjnej pamięci rekurencyjnej.

Jednym z ważniejszych parametrów pamięci autoasocjacyjnej jest jej pojemność, czyli liczba obrazów, które może efektywnie zapamiętać. Przeprowadzimy analizę pojemności pamięci przy założeniu, że wszystkie składowe wektorów wzorcowych
, i=1,2,...,n, m=1,2,...,p, są niezależnymi dyskretnymi zmiennymi losowymi, przyjmującymi wartości ±1 z prawdopodobieństwem P=1/2. w wyrażeniu (6.22) na wartość pobudzenia łącznego i-tego neuronu, nie uwzględniając zerowych wag na głównej przekątnej, kładąc s⁽⁰⁾ =
oraz wyłączając przed sumy składnik m = m', otrzymujemy:

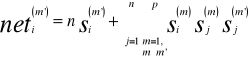
(6.28)

Wektor stanu pamięci v jest stabilny, gdy sgn(net_i)=sgn(
) = v_i i=1,2,...,n. Stąd na podstawie (6.28) widać że składowa
jest stabilna, gdy znak sumy w (6.28) jest taki sam jak znak
lub gdy znaki te są przeciwne, ale wartość sumy jest mniejsza od n.

Wprowadźmy parametr

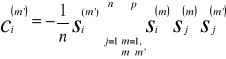
nazywany przesłuchem i będący iloczynem składowej
i sumy z wyrażenia(6.28). Łatwo zauważyć, że gdy
< 1 składowa
jest stabilna. Wyznaczymy teraz rozkład prawdopodobieństwa
, a następnie na jego podstawie różne wielkości określające pojemność sieci. Parametr
jest iloczynem zmiennej losowej s_i/n i sumy n(p-1)≈np. zmiennych losowych, przyjmujących wartości ±1 z prawdopodobieństwem P=1/2. Z rachunku prawdopodobieństwa wiadomi, że suma dwuwartościowych zmiennych losowych ma rozkład dwumianowy, który w naszym przypadku przybiera postać:

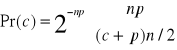
Dla dużych wartości np. rozkład ten zbliża się do rozkładu normalnego o wariancji σ² = p/n

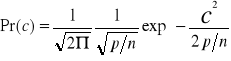
(6.29)

Rozkład ten przedstawiono na rys. 6.10.

Rys.6.10. Rozkład prawdopodobieństwa przesłuchu c. Zakreskowane pole przedstawia prawdopodobieństwo niestabilności jednej składowej.

Pr(c)

σ =

0 1

Na podstawie rozkładu (6.29) można znaleźć prawdopodobieństwo niestabilności pojedynczej składowej równe prawdopodobieństwu tego, że c > 1:

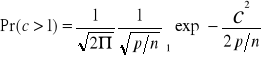
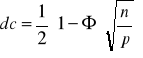
(6.30)

gdzie funkcja :

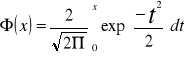
nazywa się całką prawdopodobieństwa i jej wartości są podane w tablicach. Korzystając ze wzoru 6.30 można na podstawie danego prawdopodobieństwa niestabilności obliczyć stosunek p/n. Obliczone prawdopodobieństwo niestabilności jednej składowej wskazuje tylko niestabilność początkową, natomiast nie daje informacji, czy początkowa niestabilność nie pociągnie za sobą w kolejnych krokach przełączania innych składowych. np. początkowa niestabilność 1% składowych i przyjmowanie przez nie w rezultacie przeciwnych wartości mogłyby być do przyjęcia, natomiast oczywiście nie do przyjęcia byłaby niewielka początkowa niestabilność powodująca w efekcie kilkudziesięcioprocentowy błąd. Bardziej złożone analizy przedstawiają Amit, Gutfrund i Sompolinsky; wynika z nich, że krytyczną wartością jest p/n=0,138. Dla większych wartości początkowa niewielka liczba niestabilnych składowych w kolejnych krokach lawinowo zmienia inne składowe, dając ostatecznie zupełnie błędny odczyt. W innej def. Pojemności żąda się, aby z prawdopodobieństwem P₁ bliskim jedności wszystkie wzorce były stabilne, czyli [1-Pr(c>1)]^np.>P₁. Po zastosowaniu słusznego dla dużych np przybliżenia [1-Pr(c>1)]^np≈ -Pr(c>1)np +1 warunek przybiera postać:

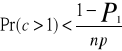
(6.31)

Dla małych p/n można zastosować rozwinięcie asymptotyczne całki prawdopodobieństwa:

dla x → ∞

Stosując to rozwinięcie oraz logarytmując obie strony nierówności 6.31 otrzymujemy:

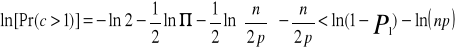
lub dla dużych n

Przybliżonym rozwiązaniem tej nierówności, zbliżającym się ze wzrostem n do rozwiązania dokładnego, jest:

(6.32)

Gdy liczba zapamiętanych obrazów p spełnia warunek 6.32, wtedy wszystkie zapamiętane obrazy są stabilne z prawdopodobieństwem bliskim jedności.

Oprócz oszacowania 6.32 McEliece i inni podali rozszerzony wzór określający pojemność pamięci:

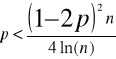
Gdzie ρ jest odległością wektorów podzieloną przez liczbę składowych n. Wzór określa liczbę wektorów wzorcowych p, do których zbieżne będą z prawdopodobieństwem bliskim jedności wektory wejściowe znajdujące się w odległości nie większej niż ρ od wektorów wzorcowych. Aczkolwiek liczba obszarów, które pamięć Hopfilelda może bezbłędnie zapamiętać przy zastosowaniu algorytmu 6.19, a później odtwarzać, jest niewielka, sieci te znajdują wiele praktycznych zastosowań.

(6.19)

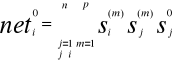
(6.22)

39.Proszę przedstawić jakie są skutki przekroczenia pojemności autoasocjacyjnej pamięci rekurencyjnej.

Przeładowanie pamięci może spowodować:

-odtwarzanie przez pamięć negacji właściwego obrazu

-mogą istnieć w pamięci nieplanowane stany stabilne (obrazy fałszywe)

-zapamiętane wektory mogą nie być stanami stabilnymi i sieć nigdy nie zdoła ich odtworzyć

40.Proszę określić, co rozumiemy pod pojęciami grupowanie i klasyfikacja.

Klasyfikacja (gdy zbiór obrazów wej dzieli się na kilka klas, to w odpowiedzi na obraz wej jest inf o klasie, do której należy obraz) Odpowiedź klasyfikatora podczas klasyfikacji.

Grupowanie

Grupowanie polega na przyporządkowaniu branego pod uwagę elementu do jednej lub wielu grup (klas, zbiorów), przy czym grupy te są wyznaczane przez sam proces grupowania na podstawie analizy danych o wszystkich dostępnych elementach, a nie jak w przypadku klasyfikacji, gdzie klasy zostały zdefiniowane wcześniej, niejako poza procesem klasyfikacji. Grupy wyznaczane są na podstawie pewnych czynników albo wskazujących na podobieństwa elementów albo opartych na przyjętych rozkładach prawdopodobieństwa, albo korzystających z jeszcze innych przesłanek.

Grupowanie jest szczególnie przydatne w rozwiązywaniu problemów segmentowania. Algorytm grupowania wyznacza czynnik dywersyfikujący elementy rozważanej populacji, definiuje grupy (segmenty) i przyporządkowuje do nich poszczególne elementy. Grupowanie jest często pierwszym etapem w eksploracji danych: po wyznaczeniu segmentów można do nich zastosować inne techniki w zależności od oczekiwanych rezultatów.

41.Proszę omówić najpopularniejsze miary podobieństwa stosowane podczas grupowania.

Najpopularniejsze miary grupowania:

• Odległość Euklidesa

||x-x_i||=sqrt((x-x_i)^t*(x-x_i))

Reguła:

Im mniejsza odległość tym większe podobieństwo.

• Kątowa miara podobieństwa

cosϕ_i­ = (x^tx_i) / ||x||*||x_i||

Gdy cosϕ₂ < cosϕ₁ obraz jest bardziej podobny do x_2­ niż do x₁ i należy go zaliczyć do grupy drugiej.

Kryterium kątowej miary podobieństwa jest skuteczna tylko wtedy, gdy długość wektorów x, x­₁ i x₂ są porównywalne, najlepiej równe ( konieczność normalizacji).

42. Proszę omówić sieć Kohonena - uczenie z rywalizacją.

Sieci samoorganizujące w procesie ucznia spontanicznie tworzą odwzorowanie (ang. mapping) zbioru sygnałów wejściowych na zbiór sygnałów wyjściowych. Cechy jakimi musi charakteryzować się sieć samoorganizująca oraz proces uczenia, to koherentność i kolektywność.

Koherentności jest to efekt grupowania danych wejściowych w klasy podobieństwa. Grupowanie w klasy podobieństwa opisywane jest przez zestaw technik matematycznych (w większości przypadków statystycznych) zwanych analizą skupień (ang. cluster analysis). Wśród technik analizy skupień na uwagę szczególnie zasługują mechanizmy kwantyzacji wektorowej.

Kolektywność jest to efekt, który zachodzi w sieciach samoorganizujących. Główne cechy tego mechanizmu to, to że co rozpoznaje jeden neuron, w dużej mierze zależy także od tego co rozpoznają inne neurony. Ten efekt związany jest z pojęciem sąsiedztwa.

Ogólna zasada uczenia sieci Kohonena opiera się na następujących założeniach:

wektor sygnałów wejściowych X jest przed procesem uczenia normalizowany ||X|| = 1, co można zapisać jako

 

 

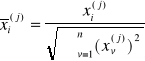
wszystkie neurony sieci dostają ten sam zestaw sygnałów wejściowych wyliczana jest odpowiedź dla wszystkich neuronów proces modyfikacji wag następuje w neuronie który zwyciężył w rywalizacji - posiada największą wartość odpowiedzi

wyliczanie nowej wartości wag dla neuronu który zwyciężył następuje według poniższego przepisu:

 

 

gdzie:

h(m,m^*) - jest funkcją określającą sąsiedztwo

ၨ^(j) - określa współczynnik uczenia dla (j)-tego kroku

Sąsiedztwo jest to metoda, która pozwala na redukcję niepożądanych skutków uczenia sieci samoorganizujących w oparciu o konkurencje. Konkurencja w procesie uczenia może doprowadzić do sytuacji takiej, że tylko niewielki odsetek neuronów uzyska możliwość rozpoznawania obiektów pokazywanych sieci (nauczy się). Reszta neuronów nie będzie w trakcie uczenia zmieniać swoich wag i w ten sposób zatraci na zawsze swe użytkowe cech jako elementy wytrenowanej sieci neuronowej. Sąsiedztwo jest miarą w jakim stopniu sąsiad neuronu zwycięskiego będzie miał zmieniane wagi w danym kroku procesu uczenia. Zwykle wartość tego parametru jest określana na wartość 0 - 1.

Sąsiedztwo rozpatruje się w układach:

•         jednowymiarowych, neurony sąsiednie leżą na jednej linii,

•         dwuwymiarowych, neurony są ułożone w warstwie a sąsiadami są neurony położone na lewo i na prawo oraz u góry i u dołu rozpatrywanego neuronu, inny przypadek opisuje dodatkowe kontakty po przekątnych

•         wielowymiarowe, neurony ułożone są swobodnie w przestrzeniach wielowymiarowych a twórca danej sieci określa zasady sąsiedztwa.

Do najbardziej istotnych i użytecznych układów sąsiedztwa zaliczamy organizacje jedno- i dwuwymiarowe, dla nich właśnie dodatkowym istotnym parametrem jest określenie ile neuronów obok (sąsiadów z lewej, prawej itd.) ma podlegać uczeniu w przypadku zwycięstwa danego neuronu.

Po raz pierwszy opracowania na temat sieci samoorganizujących z konkurencją i sąsiedztwem pojawiły się w latach 70-tych za przyczyną opisów eksperymentów fińskiego badacza Kohonena. Stąd też tego typu sieci wraz z metodami uczenia nazywamy sieciami Kohonena.

43. Podaj, jak w MATLAB'ie zapisać zmienne z przestrzeni roboczej do zewnętrznych plików typu ASCII i wyjaśnić co oznacza poniższe polecenie: load b.dat

Aby zapisać do zbioru ASCII tekstów wypisywanych przez MATLAB w jego oknie poleceń używa się polecenia: diary nazwa_zbioru.

Użyć polecenia save w postaci:

save nazwa_pliku nazwa_zmiennych -ascii -double

Plik wczytuje się poleceniem:

load nazwa_pliku.rozszerzenie

Nazwa zmiennej (wprowadzona do przestrzeni roboczej) jest identyczna z nazwą wczytanego pliku.

Polecenie load b.dat spowoduje odczytanie pliku binarnego o nazwie b.dat. Taki plik może zawierać macierze wygenerowane wcześniej podczas pracy z MATLAB-em lub pliki tekstowe zawierające dane numeryczne. Plik tekstowy powinien być zorganizowany jako prostokątna tabela liczb oddzielonych spacjami, zawierająca jeden wiersz w linii i taką sama ilość elementów w każdym wierszu.

Przykładowo, utwórz poza MATLAB-em plik tekstowy, zawierający cztery poniższe linie:

16.0 3.0 2.0 13.0

5.0 10.0 11.0 8.0

9.0 6.0 7.0 12.0

4.0 15.0 14.0 1.0

Zapisz plik pod nazwą b.dat. Następnie wpisz komendę

load b.dat

co spowoduje odczytanie pliku oraz utworzenie zmiennej b, zawierającej naszą przykładową macierz.

44.Wyjaśnić pojęcia MAT-plik i M.-plik

• M-pliki, umożliwiające definiowanie własnych poleceń i algorytmów obliczeniowych (napisany w kodzie ASCII)

• MAT-pliki służą do wymiany danych i wyników obliczeń pomiędzy MATLAB-em, a innymi programami (plik binarny)

45. Pliki skryptowe i funkcyjne

Skrypt - zbiór tekstowy zawierający instrukcje (polecenia), które mają być wykonane przez interpreter, dla wszystkich skryptów przyjęto standardowe rozszerzenie .m. Skrypt nie musi spełniać żadnych dodatkowych wymogów formalnych poza poprawnością składniową i semantyczną znajdujących się w nim poleceń.

Funkcje - mamy możliwość nie tylko wykorzystania funkcji napisanych przez innych (biblioteki i funkcje standardowe), funkcje możemy tworzyć samodzielnie. Dzięki temu MATLAB wykazuje własności zbliżone do języków strukturalnych - umożliwia zamknięcie pewnej funkcjonalnej całości o obrębie jednej funkcji, a następnie wielokrotne jej wykorzystanie. Definicję funkcji umieszczamy w skrypcie o identycznej nazwie z nazwą definiowanej funkcji i rozszerzeniem .m.

48. Przedstaw jaki jest priorytet operatorów w MATLAB'ie

Priorytet (kolejność działania) operatorów w MATLAB-ie jest. następujący:

• operatory arytmetyczne,

• operatory relacji,

• operatory logiczne

Ilustrują to poniższe przykłady:

1 & 0 + 3 zapis równoważny 1 & (0 + 3)

3 > 4 & 1 zapis równoważny (3 > 4) & 1

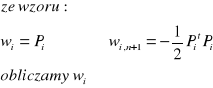
w₁₂

w_R,n+1

w_R

w_2,n+1,

w₂₂

w_1.n+1

w₁

w₁₁

dyskryminaty

g_R(x)

g₂(x)

g₁(x)

Obraz x

klasa

1

2

Slektor max

R

w_R2

w₂

w₂₁

w_R1

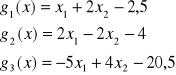
1

2

sektor

maksimum

R

g_R(x)

g₂(x)

g₁(x)

równoległobok

heteroasocjacja

kwadrat lub niekompletny kwadrat

obraz wejściowy

0

x 8

{ }

y

x

sieć adaptacyjna

d - porządana odpowiedź

x

sieć adaptacyjna

y

obliczenie odległości

-1

-1

-1

y

1

1

1

X₃

X₂

X₁

y

-1

1

1

1

X₃

X₂

X₁

W_ii+-1

I=1,2,n

W₃

W₂

W₁

X₃

X₂

X₁

Przy czym to „l” we wzorach to jest raczej „ł”

nr klasy

obraz wej

{ x }

---