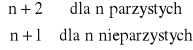Obliczanie całek metodą Monte-Carlo
Metoda Monte Carlo - całka pojedyncza
Mamy obliczyć przybliżoną wartość In całki oznaczonej
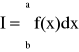
(129)
przy założenie, że f(x) jest funkcją ciągłą w przedziale domkniętym [a;b]
Następnie n-krotnie generujemy realizację x zmiennej losowej X o rozkładzie równomiernym w przedziale [a,b], otrzymujemy w rezultacie ciąg liczb x1, x2, ..., xn,
Przybliżoną wartość całki określa wzór
![]()
(130)
Zbieżność przybliżonej wartości całki In do jej dokładnej wartości jest gwarantowana w sensie probalistycznym, tzn., że dla każdego ε>0 zachodzi relacja:
![]()
(131)
gdzie P jest prawdopodobieństwem, przy czym błąd metody monte Carlo można określić wzorem
![]()
(132)
Maszyny typowe zazwyczaj dysponują generatorem liczb losowych o rozkładzie równomiernym w przedziale [0,1], zachodzi zatem konieczność przeliczania wylosowanej realizacji Y z przedziału [0,1], na realizację zmiennej losowej X o rozkładzie równomiernym w przedziale [a, b]. Wzory poniżej, to ilustrują:
Przeliczanie zmiennych losowych Y na X
X=(b-a)Y+a (133)
Przeliczanie realizacji zmiennych losowych Y na X
x=(b-a)y+a (134)
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Równania różniczkowe zwyczajne z warunkami początkowymi
Równania różniczkowe są wykorzystywane do odwzorowania wielu problemów z zakresu różnych nauk, które dotyczą zmian jednej zmiennej względem innej zmiennej. Wiele problemów świata rzeczywistego opisywanych przez równania różniczkowe jest za bardzo złożonych, aby uzyskać rozwiązanie dokładne (analityczne), należy znaleźć rozwiązanie przybliżone. Są dwa sposoby aby uzyskać rozwiązanie przybliżone. Po pierwsze można dokonać uproszczenia zadanego równania różniczkowego do takiej postaci, dla której znamy rozwiązanie dokładne, wówczas uproszczone równanie będzie przybliżało rozwiązanie równania zadanego. Drugim sposobem jest zastosowanie jednej z metod numerycznych w celu przybliżenia rozwiązania zadanego równania.
Metody różnicowe jednokrokowe:
metody Eulera;
metody Rundego-Kutty
metody Rundego-Kutty-Fehenberga
Metoda Eulera
Rozpatrzmy zadanie znalezienia funkcji y=y(t), które dla ![]()
spełnia równanie różniczkowe zwyczajne pierwszego rzędu:
![]()
(7)
oraz warunek początkowy
y(a)=y0 (8),
gdzie f jest daną funkcją dwu zmiennych. Warunek wystarczający istnienia i jednoznaczności rozwiązania zadania (7) oraz (8) jest warunek ciągłości funkcji f(t,y)
Metoda ta rzadko jest używana w praktyce, natomiast ze względu na jej prostotę, zostanie przedstawiona w celu zobrazowania i zrozumienia technik stosowanych w bardziej zaawansowanych metodach, pomijając przy tym złożone działania matematyczne. Przedmiotem rozważań będzie poniższe równanie.
![]()
, gdzie ![]()
oraz y(a)=a (10)
Na rozwiązanie powyższego zagadnienia będziemy obliczać przybliżone wartości funkcji yi=y(ti), gdzie ti=a+ih, h=(b-a)/N, dla którego i=(0,1, ..., N), gdzie ti nazywane są punktami węzłowymi, natomiast h odległością między nimi.
Rozwiniemy y(t) w szereg Taylora w celu wyprowadzenia metody Eulera. Zakładając, że y(t) jest jedynym rozwiązaniem (10) oraz posiada drugą pochodną, która jest ciągła w przedziale [a, b] wówczas dla każdego i=1, 2, ..., N.
Wykorzystując powyższe założenia możemy zapisać:
![]()
(11), gdzie ![]()
Oznaczamy h=ti+1-ti, wówczas otrzymujemy:
![]()
(12)
Użyjemy podstawienia y'(t)=f(t, y), wówczas otrzymujemy:
![]()
(13)
Zapisując ωi≈y(ti) oraz pomijając błąd przybliżenia otrzymujemy ωi+1=ωi+hf(ti, ωi) (14)
Powyższy wzór nazywamy metodą Eulera - wzór ten nazywany jest inaczej równaniem różniczkowym, gdyż można zapisać:
![]()
(15)
Aby wyznaczyć wartość szukanej funkcji y(x) w następnym kroku h, wykorzystujemy poprzednią wartość funkcji oraz wielkości zmian funkcji - dzięki pochodnej. Natomiast uwzględniając błąd przybliżenia wzór (13) przyjmuje postać:
![]()
, gdzie ![]()
(16)
Lokalny błąd dyskretyzacji τi+1(h)
![]()
(17)
dodatkowo możemy określić krok h, dla którego błąd lokalny jest mniejszy od zadanej dokładności δ
![]()
, gdzie ![]()
Globalny błąd dyskretyzacji g(x)
g(t)= ω(t)-y(t) (19)
Dla wybranego punktu ti możemy zapisać:
gi=ωi-y(ti) (20), wówczas
![]()
, gdzie L- liczba Lipschnitz`a
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Metoda Eulera - wstecz
Powyższe rozważania dotyczyły metody Eulera w przód, ponieważ krok spełniał warunek h>0. W analogiczny sposób można wyprowadzić metodą Eulera wstecz przyjmując h<0, wówczas otrzymujemy:
wi+1 = wi + hf (ti+1, wi+1) (22)
wi+1(k) = wi + hf (ti+1, wi+1(k-1)) (23)
Metoda wstecz różni się w stosunku do metody w przód argumentami funkcji f.
Metoda w przód wykorzystuje do obliczenia przybliżenia wartości z poprzedniego kroku, natomiast metoda wstecz jest równaniem uwikłanym, ponieważ aby obliczyć kolejne przybliżenie wi+1 wykorzystujemy wartości z poprzedniego kroku oraz poszukiwaną wartość wi+1. Takiego równania nie można rozwiązać w sposób bezpośredni. Aby rozwiązać takie równanie (23) należy zastosować proces iteracyjny, czyli poszukujemy kilkakrotnie wi+1(k), stojącej po prawej stronie równania podstawiając jako wi+1(k-1) - lewa strona równania, wynik przybliżenia z poprzedniej iteracji (k-1). Proces trwa do momentu, kiedy spełniony zostanie warunek:
|wi+1(k) - wi+1(k-1)| ≤ ε (24)
gdzie ε - tolerancja obliczeń
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Metody Rungego-Kutty
Powszechnie na całym świecie stosuje się metody Rungego-Kutty czwartego rzędu. Polegają one na rozwiązaniu zagadnienia:
![]()
gdzie t∈ [a,b] oraz y(a)=α (25)
i przedstawieniu różnicy funkcji y(t) w punktach ti+1 oraz ti w postaci:
wi+1 - wi = ![]()
lub inaczej wi+1 - wi = h0 (ti,wi,h) (26)
gdzie m oznacza rząd metody, cj są stałymi, a
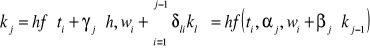
gdzie αj, βj, γj, δlj - stałe
h - krok całkowania
Określenie stałych cj, αj, βj otrzymujemy poprzez rozwinięcie funkcji f(t,y) w szereg Taylora w otoczeniu punktu ti
Metody R-K - metoda 2 rzędu
Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 2 rzędu pozwala określić stałe c1, α1,β1, c2, α2, β2 :
Metoda punktu środkowego:
C1 = 0 C2 = 1 α1 = 0 α2 = h/2 β1 = 0 β2 = ½ (28)
wówczas możemy zapisać:
k1=hf (ti,wi) k2=hf (ti + ½ h, wi + ½ k1)
ostatecznie:
wi+1=wi+k2
lub
wi+1=wi + hf(ti + h/2, wi + h/2 * f(ti, wi))
Interpretacja graficzna:
f1=f(ti,wi) f2=f(ti + h/2, wi + h/2 * f1)
Stosując metody Rungego-Kutty 2 rzędu , rozwiązać następujące równanie różniczkowe:
y'=y-t2 + 1 0≤ t ≤2 y(0)=0,5
dla N = 10 wtedy h = 0,2; ti = i⋅h ; w0 = 0,5 oraz
metoda punktu środkowego wi+1 = 1,22 wi - 0,0088 i2 + 0,218
Metoda zmodyfikowana Eulera
wi+1 = 1,22 wi - 0,0088 i2 + 0,216
Metoda Heana dla i = 0, 1, ..., 9
wi+1 = 1,22 wi - 0,0088 i2 + 0,2173
Rozwiązanie dokładne ma postać:
y(t) = (t2+1) - 0,5 et
Metody R-K rzędu 4
Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 4 rzędu, pozwala określić stałe we wzorze (wzór ogólny R-K). Poniżej przedstawiono najczęściej stosowaną metodę 4 rzędu
k1 = hf (ti, wi)
k2 = hf (ti + ½ *h, wi + ½ *k1)
k3 = hf (ti + ½ *h, wi + ½ *k2) (37)
k4 = hf (ti+h, wi+k3)
ostatecznie:
wi+1=wi + 1/6 (k1 + 2k2 + 2k3 + k4) (38)
Interpretacja graficzna:
f1 = f (ti, wi)
f2 = f (ti + ½ * h, wi+1 + h f1)
f3 = f (ti + ½ * h, wi + ½ * h f2)
f4 = f (ti + h, wi + h f3)
linia 3-4 nie jest łamana - jest prosta !!! (na 99%) :)
Metoda R-K jest najczęściej stosowaną metodą do rozwiązywania układów równań różniczkowych
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Kwadratury z ustalonymi węzłami
Kwadratury Newtona-Cotesa
Całkowanie z zastosowaniem kwadratur o ustalonych węzłach polega na zastąpieniu funkcji podcałkowej wielomianem interpolacyjnym Lagrange'a Li(x).
Jeżeli dla skończonego przedziału [a,b] wybierzemy zbiór punktów węzłowych {x0, ..., xn} takich, że:
xi = x0 + i · h
gdzie:
![]()
dla wówczas=(0, 1, …, n)
n - oznacza również stopień wielomianu interpolacyjnego
![]()
(5), gdzie:
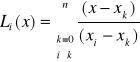
(6)
wówczas
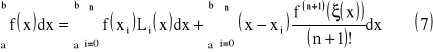
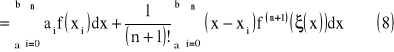
ξ - dowolny punkt pośredni z przedziału (x,xi)
gdzie:
![]()
oraz 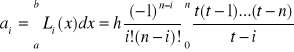
(9)
ostatecznie wzór kwadratury Newtona - Cotesa oraz reszta kwadratury
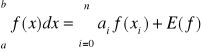
(10)
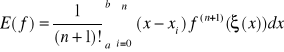
(11)
Twierdzenie 1
Kwadratury Newtona-Cotesa oparte na n+1 węzłach są rzędu
|
wówczas wzory kwadratur dla n parzystych mają postać
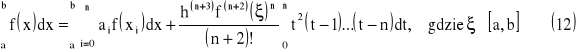
oraz dla nieparzystych mają postać:
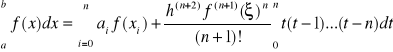
(13)
Kwadratury z ustalonymi węzłami - wzór trapezów
Wyznaczmy wzór kwadratury dla n = 1
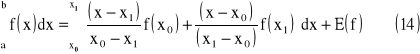
gdzie:
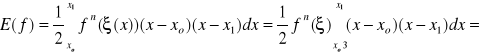
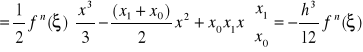
wówczas:
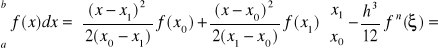
![]()
(16)
Ostatecznie otrzymujemy

powyższe równanie jest znane jako wzór trapezów - widać, że wzór pozwala dokładnie obliczyć całkę dla dowolnej funkcji, dla której druga pochodna jest zero (wtedy reszta jest 0).
Zauważmy, że dla powyższych rozwiązań końce przedziału całkowania są węzłami kwadratury x0=a oraz xn=b. Wzory kwadratur oparte na tych węzłach nazywamy wzorami zamkniętymi Newtona - Cotesa.
Podobnie wyznaczyć można wzory dla innych n.
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Kwadratury Newtona-Cotesa - wzory zamknięte
Poniżej znajdują się wzory zamknięte dla n = (1..3):
wzór trapezów 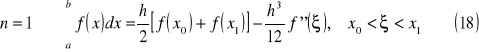
wzór parabol (Simpsona)
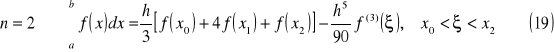
wzór Bessela
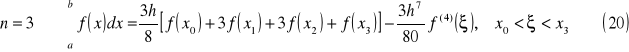
Interpretacja graficzna
wzór parabol (Simpsona)
wzór Bessela
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Kwadratury Newtona - Cotesa - wzory otwarte
Wzory kwadratur nie opartych na węzłach będących końcami przedziału całkowania nazywamy wzorami otwartymi Newtona - Cotesa
Jeżeli dla skończonego [a ; b] przedziału wybierzemy zbiór punktów węzłowych {x0, …, xn} takich, że :
![]()
gdzie:
![]()
dla i=(0, …, n)
oraz
![]()
W oparciu o Twierdzenie 1 można również wyznaczyć wzory kwadratur otwartych. Wówczas wzory kwadratur dla n parzystych mają postać

oraz dla n nieparzystych mają postać:
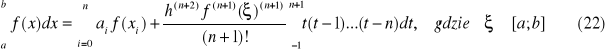
wzór prostokątów
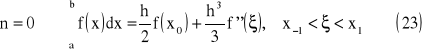

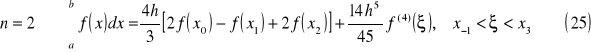

Interpretacja geometryczna
wzór prostokątów
wzór trapezów
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Kwadratury Gaussa
W poprzednim rozdziale omawiane były metody Newtona-Cotesa, które bazowały na całkowaniu wielomianu interpolacyjnego stopnia n. Pozwalał on na dokładne przybliżenie całki dla funkcji stopnia (n+1) lub (n+2). Wszystkie metody Newtona-Cotesa wykorzystywały wartości funkcji dla punktów węzłów równoległych. Ten warunek jest dogodny dla konstrukcji złożonych wzorów, ale może znacząco zmniejszyć dokładność przybliżenia całek.
Poniżej widać kwadraturę Newtona-Cotesa opartą na końcach przedziału - przybliżenie funkcji nie jest dokładne
Kwadratury Gaussa dobierają takie węzły, aby osiągnąć optymalne przybliżenie całki: 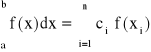
Węzły kwadratury x1, x2,..., xn z przedziału całkowania [a,b] oraz współczynniki c1, c2,...,cn są tak dobrane, aby zminimalizować błąd przybliżenia. Nie zakładamy jednak żadnych ograniczeń na węzły xi o współczynnikach ci natomiast chcemy zmaksymalizować rząd kwadratury.
Mamy znaleźć 2n stałe we wzorze, przypuszczamy więc, że rząd kwadratury powinien wynosić 2n, a więc wzór powinien być dokładny dla wielomianów stopnia (2n-1). Dla wielomianu stopnia równego lub wyższego od (2n-1) należy uwzględnić resztę kwadratury E:
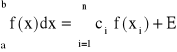
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Interpolacja Lagrange'a
Przedstawiony powyżej sposób podejścia do interpolacji nie jest zbyt efektywny, ponieważ macierz X jest macierzą pełną i nie zawsze dobrze uwarunkowaną, co oznacza, że numeryczna procedura jej odwracania może być obarczona dużym błędem.
W interpolacji wielomianowej Lagrange'a dla n+1 węzłów interpolacji
![]()
przyjmuje się funkcje bazowe w postaci

Funkcje te są wielomianami stopnia n zbudowanymi w ten sposób, że w funkcji bazowej φ1 brakuje czynnika (x-xi). Zatem wielomian interpolacji wyraża się następującym wzorem:
![]()
współczynniki a0 ... an tego wielomianu wyznaczamy z równania:
X · A = Y, przy czym macierz X ma postać:
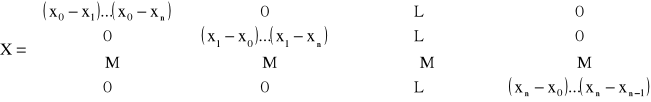
Macierz posiada tylko główną przekątną niezerową w związku z tym układ równań X · A = Y rozwiązuje się natychmiastowo

Można więc wielomian interpolacyjny Lagrange'a zapisać w postaci ułamka:
![]()
lub krócej

, j = 0, 1, ..., n
Przykład:
Wyznaczyć wielomian interpolacyjny Lagrange'a funkcji f (x) = ex w przedziale [0,2 ; 0,5] mając dane:
f (0,2) = 1,2214, f (0,4) = 1,4918, f (0,5) = 1,6487

algorytm do wyznaczania wielomianu Lagrange'a dla podanego punktu:
begin
fx:=0;
for i:=0 to n do
begin
p:=1;
for k:=0 to n do
if k<>i then p:=p*(xx-x[k])/(x[i]-x[k]);
fx:=fx+f[i]*p
end;
end;
Należy pamiętać, ze przed przystąpieniem do obliczeń należy sprawdzić czy w wektorze x wartości się nie powtarzają, ponieważ grozi to wystąpieniem błędu dzielenia przez zero.
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Aproksymacja średniokwadratowa
Niech dana będzie funkcja y=f(x), która w pewnym zbiorze X punktów x0, x1, ..., xn przyjmuje wartości y0, y1, ..., yn. Wartości te znane tylko w przybliżeniu z pewnym błędem (np. jako wyniki pomiarów). Poszukujemy takiej funkcji Q(x) przybliżającej daną funkcję f(x), która umożliwi wygładzenie funkcji f(x), czyli pozwoli z zakłóconych błędami danymi wartości funkcji przybliżonej otrzymać gładką funkcję przybliżającą.
Niech ϕj(x), j=0, 1,...,n będzie układem funkcji bazowych. Poszukujemy wielomianu uogólnionego Q(x) będącego najlepszym przybliżeniem średniokwadratowym funkcji f(x) na zbiorze X=(xj). Funkcja przybliżająca ma postać
![]()
Przy czym współczynniki ai są tak określone, aby wyrażenie
![]()
![]()
dla i=0, 1, ..., n
było minimalne. Funkcja w(x) jest z góry ustaloną funkcją wagową.
Aby wyznaczyć współczynniki ai oznaczamy odchylenie
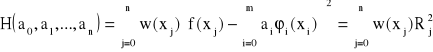
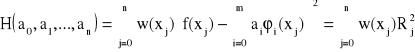
gdzie Rj jest odchyleniem w punkcie xj.
Następnie obliczamy pochodne cząstkowe funkcji H względem ai. Z warunku
![]()
, gdzie k = 0, 1, ..., n
otrzymujemy układ m+1 równań o niewiadomych ai zwany układem normalnym
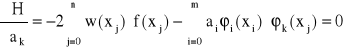
, gdzie k = 0, 1, ..., n
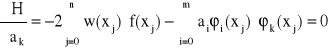
Jeśli wyznacznik tego układu jest różny od zera to rozwiązaniem układu jest minimum funkcji H. W zapisie macierzowym układ przyjmuje postać
![]()
gdzie
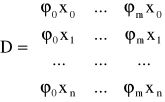

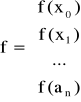
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Równania paraboliczne - Dyfuzja
Równania różniczkowe cząstkowe paraboliczne znane jako równanie dyfuzji lub przewodnictwa, w zależności od jednego wymiaru oraz czasu przyjmuje postać:
![]()
![]()
![]()
dla oraz (13)
![]()
![]()
z warunkami brzegowymi dla
![]()
![]()
i początkowymi dla
Równania tego typu są stosowane dla różnych problemów fizycznych, które są zależne od czasu. Najczęściej stosowane są do obliczenia przepływu ciepła wzdłuż pręta o długości l, przy założeniu że, powierzchnia boczna pręta jest odizolowana od otoczenia. Stała ၡ jest niezależna od położenia oraz czasu i najczęściej określa przewodność cieplną materiału z którego zrobiony jest pręt. Funkcja f określa początkowy rozkład temperatury w pręcie.
Aby rozwiązać równanie cząstkowe paraboliczne (13) zastosujemy metodę różnic skończonych MRS.

W tym celu weźmiemy liczbę całkowitą m i zdefiniujemy krok całkowania h = (b-a)/m. Dodatkowo ustalimy wartość kroku czasowego k. Dzięki temu możemy wyznaczyć węzły siatki (xi , tj ), gdzie:
![]()
![]()
dla i = 0,1, .. m oraz dla j = 0,1, ..
Dla wewnętrznych punktów węzłowych (xi,tj), które nie należą do brzegu, zastosujemy metodę różnic skończonych - MRS. Metoda ta opiera się na zastąpieniu pochodnych cząstkowych rozwinięciem funkcji w szereg Taylora w otoczeniu punktu (xi,tj) - (patrz pierwsza i druga pochodna numeryczna) . Wówczas otrzymujemy:
![]()
Dla zmiennej x (14)
![]()
gdzie:
![]()
Dla zmiennej t (15)
![]()
gdzie:
Podstawiając wzory (14) oraz (15) do równania dyfuzji (13) oraz wyłączając oszacowanie błędu zapisujemy:
![]()
(16)
![]()
warunek brzegowy : (17)
dla i = 1,2 … m-1 oraz j = 1,2, …
natomiast lokalny błąd odcięcia jest równy :
![]()
(18)
![]()
![]()
gdzie: oraz
Ostatecznie wzór na MRS, podstawiając za ( xi , tj ) = wi,j oraz wyłączając oszacowanie błędu zapisujemy:
![]()
(19)
przekształcając powyższy wzór ze względu na wi,j+1 ,wówczas otrzymujemy:
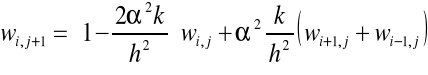
(20)

lub
![]()
gdzie: (21)
dla i = 1,2 … m-1 oraz j = 1,2, …
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
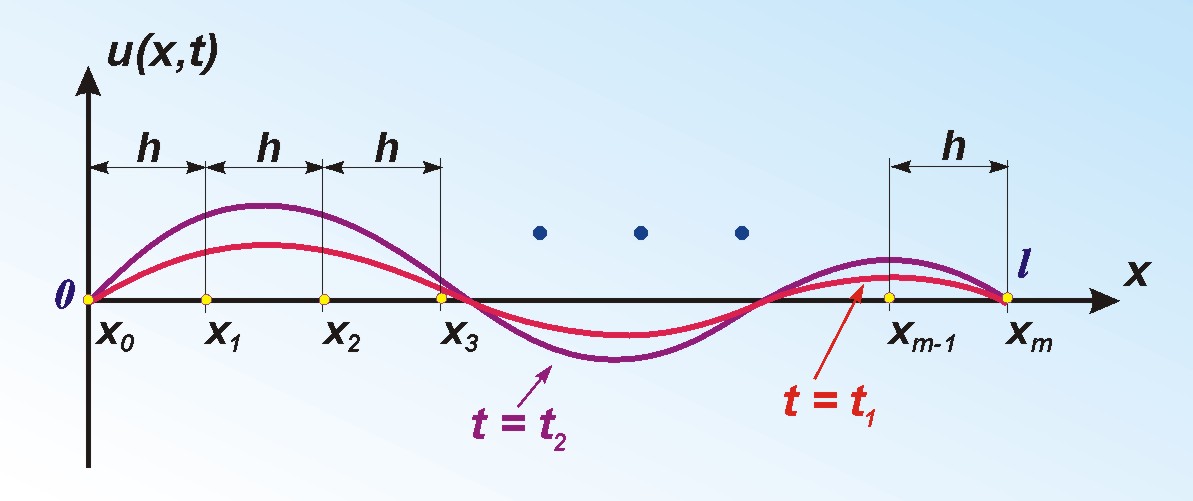
Równanie hiperboliczne - Falowe
Równania różniczkowe cząstkowe hiperboliczne znane jako równanie falowe, w zależności od jednego wymiaru oraz czasu przyjmuje postać:
![]()
(32)
![]()
![]()
dla oraz
![]()
![]()
z warunkami brzegowymi dla
![]()
![]()
![]()
i początkowymi oraz dla
Równania tego typu są stosowane dla różnych problemów fizycznych, które są zależne od czasu. Najczęściej stosowane są do obliczenia wartości fali płaskiej w dowolnym punkcie pomiędzy 0 a l dla dowolnej chwili czasu większej od zera. Funkcje f(x) i g(x) określają warunki początkowe położenia oraz prędkości rozchodzenia się fali.
Aby rozwiązać równanie cząstkowe paraboliczne (32) zastosujemy metodę różnic skończonych MRS.
W tym celu weźmiemy liczbę całkowitą m i zdefiniujemy krok całkowania h = (b-a)/m. Dodatkowo ustalimy wartość kroku czasowego k. Dzięki temu możemy wyznaczyć węzły siatki (xi , tj ), gdzie:
![]()
![]()
dla i = 0,1, .. m oraz dla j = 0,1, ..
Dla wewnętrznych punktów węzłowych (xi,tj), które nie należą do brzegu, zastosujemy metodę różnic skończonych - MRS. Metoda ta opiera się na zastąpieniu pochodnych cząstkowych rozwinięciem funkcji w szereg Taylora w otoczeniu punktu (xi,tj) - (patrz druga pochodna numeryczna) . Wówczas otrzymujemy:
![]()
Dla zmiennej x (33)
![]()
gdzie
![]()
Dla zmiennej t (34)
![]()
gdzie
Podstawiając wzory (33) oraz (34) do równania falowego (31) oraz wyłączając oszacowanie błędu zapisujemy:
![]()
(35)
![]()
warunek brzegowy : (36)
dla i = 1,2 … m-1 oraz j = 1,2, …
natomiast lokalny błąd odcięcia jest równy :

(37)
![]()
![]()
gdzie: oraz
Ostatecznie wzór na MRS, podstawiając za ( xi , tj ) = wi,j zapisujemy:
![]()
(38)
przekształcając powyższy wzór ze względu na wi,j+1 ,wówczas otrzymujemy:
![]()
![]()
gdzie: (39)
dla i = 1,2 … m-1 oraz j = 1,2, …
![]()
z warunkami brzegowymi dla j = 1,2, …
![]()
i początkowymi dla i = 1,2, … m-1
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Numeryczne rozwiązywanie równań nieliniowych
Metoda Newtona
Dany jest układ równań nieliniowych z n niewiadomymi
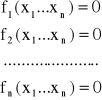
który możemy zapisać w postaci wektorowej
f(x)=0
gdzie:
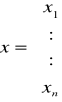
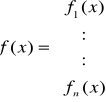
O funkcjach fi(x1...xn) dla i = 1, 2, ..., n zakładamy, że mają ciągłe pochodne pierwszego rzędu w pewnym obszarze zawierającym odosobniony pierwiastek układu równań. Niech
x(k) = {x1(k), ..., xn(k)}
będzie k-tym przybliżeniem pierwiastka a = {a1, ..., an} równania.
Dokładną wartość pierwiastka wyraża wzór a = x(k) + ε(k)
Gdzie ![]()
jest błędem pierwiastka przybliżonego ![]()
. Skoro istnieje ciągła pochodna funkcji f(x) możemy zapisać:
![]()
Zastępując błąd ![]()
przyrostem ![]()
i porównując prawą stronę powyższego wyrażenia do zera otrzymujemy równanie liniowe:
![]()
Wzór ten stanowi zapis rekurencyjny dla metody Newtona w postaci macierzowej.
Pochodna f'(x) jest macierzą Jakobiego
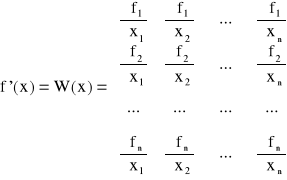
Przyjmując, że ![]()
jest macierzą nieosobliwą możemy równanie liniowe przekształcić do postaci:
![]()
stąd przyjmując dowolną wartość ![]()
otrzymujemy ciąg kolejnych przybliżeń pierwiastka równania ![]()
uzyskanych metodą Newtona.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
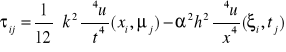
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka