3EKRAN_52

Lekcja 4-Transfiguracja trójkąt-gwiazda i metoda Thevenina

W lekcji 4 sformułowano twierdzenie o równoważności n-wrotników, które następnie zostało wykorzystane do wyprowadzenia wzorów na transfigurację trójkąt-gwiazda.

Dodatkowo oprócz twierdzenia Thevenina przeprowadzono rozważania dotyczące charakterystyk obciążenia źródeł rzeczywistych. Wyprowadzono również warunek równowagi tych źródeł. Lekcja zawiera rozwiązane przykłady, oraz postawiono pewne pytania problemowe.

3EKRAN_53

Transfiguracja gwiazda trójkąt

Równoważność n-wrotników zachodzi, gdy:

1. Mają jednakową liczbę zacisków.

2. Ich rezystancje wypadkowe mierzone między dwoma dowolnymi parami odpowiadających sobie zacisków są jednakowe.

3. Napięcia w stanie jałowym odpowiadającym sobie parom zacisków są równe.

3EKRAN_54

Równoważność trójników pasywnych- transfiguracja gwiazda-trójkąt

Dla wyprowadzenia wzorów transfiguracji gwiazda-trójkąt wystarczy zbadać punkt 1 i 2.

3EKRAN_55

Inny sposób rysowania gwiazdy i trójkąta

3EKRAN_56

Wyprowadzenie wzorów na transfigurację gwiazda-trójkąt

Dla zacisków 1-2.

R₁+R₂ =

Dla zacisków 2-3.

R₂ +R₃ =

Dla zacisków 1-3.

R₃+R₁
=

Komentarz-EKRAN_56

Określając rezystancje widziane z punktu widzenia wybranej pary zacisków dla gwiazdy oraz rezystancje odpowiadającym zaciskom dla trójkąta otrzymamy układ trzech równań, z których możemy obliczyć rezystancje trójkąta względem gwiazdy lub odwrotnie.

3EKRAN_57

Transfiguracja gwiazda trójkąt

3EKRAN_58

Transfiguracja trójkąt-gwiazda

Rozwiązując powyższy układ ze względu na zmienne R₁,R₂,R₃ otrzymamy:

W przypadku, gdy R₁=R₂=R₃=R_ otrzymamy

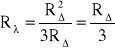
Komentarz-EKRAN_58

Uzyskane wzory noszą nazwę transfiguracji gwiazda-trójkąt i pozwalają na obliczenie rezystancji zastępczej dowolnie połączonych dwójników. Wzory te okażą się prawdziwe również dla obwodów prądu zmiennego.

3EKRAN_59

Przykład 3.4 Obliczyć wskazanie amperomierza.

Komentarz-EKRAN_59

Zaznaczony trójkąt zostanie zamieniony na gwiazdę zgodnie z wyprowadzonymi wzorami na transfigurację.

3EKRAN_60

Komentarz-EKRAN_60

Dzięki transfiguracji możemy dokonać zwinięcia obwodu stosując odpowiednio połączenia szeregowe i równoległe.

3EKRAN_61

Zatem wskazanie amperomierza obliczamy na podstawie poniższego schematu:

Odpowiedź:

3EKRAN_62

Źródła rzeczywiste

Komentarz-EKRAN_62

W przykładzie 3.3 zastosowano już źródło rzeczywiste zasilające żarówki. Zwróć uwagę że woltomierz pokaże niższe napięcie w przypadku włączonej rezystancji w porównaniu z napięciem jakie wskazuje (E) przy jej braku (stan jałowy).

3EKRAN_63

Napięcie na zaciskach źródła rzeczewistego w funkcji obciążenia R:

Komentarz-EKRAN_63

Zbadanie granicy i pochodnej funkcji U(R) pozwoli na jej wyznaczenie

3EKRAN_64

Przebieg napięcia na zaciskach rzeczywistego źródła napięciowego w funkcji rezystancji obciążenia.

Komentarz-EKRAN_64

Warto zapamiętać, że jeżeli rezystancja obciążenia jest równa rezystancji wewnętrznej źródła rzeczywistego to spadek napięcia na nim wynosi aż 50%. Okaże się, że rezystancja R_w ma jeszcze inną własność.

3EKRAN_65

Charakterystyka zewnętrzna U=f(I)

U(I)=E-IR_W U(0)=E - stan jałowy
- stan zwarcia

Charakterystyka zewnętrzna i charakterystyki obciążenia

Komentarz-EKRAN_65

Charakterystyka zewnętrzna źródła rzeczywistego jest malejącą linią prostą.

3EKRAN_66

Źródła prądowe rzeczywiste

G_z=G_W+G

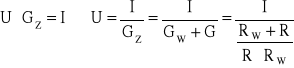
ponieważ
stąd

Komentarz-EKRAN_67

Analogicznie jak dla źródła napięciowego można wyznaczyć funkcję prądu od obciążenia.

3EKRAN_68

Przebieg prądu rzeczywistego źródła prądowego w funkcji obciążenia rezystancją R

Komentarz-EKRAN_68

Porównując otrzymaną charakterystykę obciążenia dla źródła prądowego z analogiczną charakterystyką dla źródła napięciowego można powiedzieć, że to pierwsze ma lepsze własności dla małych rezystancji R<R_w tzn. że szybciej rzeczywiste źródło prądowe można przybliżyć idealną siła prądomotoryczną SPM. Z kolei dla rezystancji R>Rw rzeczywiste źródło napięciowe szybciej można aproksymować idealną siłą elektromotoryczą SEM.

3EKRAN_69

Zadanie

a) Obliczyć dla jakich rezystancji napięcie na zaciskach źródła napięciowego nie zmniejszy się poniżej 95% napięcia stanu jałowego (E).

b) Z kolei dla jakich rezystancji, prąd źródła nie zmniejszy się poniżej 95% prądu zwarcia.

Odpowiedź-EKRAN_69

Ad.a) R>19R_w Ad.b) R<

Należy zwrócić uwagę, że w pierwszym przypadku rzeczywiste źródło napięciowe można przybliżyć idealną siłą elektromotoryczną, natomiast w drugim idealną siła prądomotoryczną.

3EKRAN_70

Równoważność źródła napięciowego i prądowego

Badamy źródło prądowe o parametrach:

-Stan jałowy I_A=I=5A - Stan zwarcia

3EKRAN_71

Jeżeli dokonamy analogicznych pomiarów zwarcia i stanu jałowego dla źródła napięciowego o parametrach spełniającego warunki:


to otrzymamy identyczne wyniki, zatem poniższe źródła będą wówczas równoważne.

Zatem

są to warunki równoważności źródeł napięciowego i prądowego (tylko rzeczywistych)!

3EKRAN_72

Niech dany będzie następujący obwód. Obliczmy wskazania woltomierza, a później amperomierza.

Komentarz-EKRAN_72

Jak widać wskazania mierników są identyczne jak w przykładach z równoważnymi źródłami rzeczywistymi.

Wniosek: Każdy fragment obwodu, w którym wyodrębniono dwa zaciski można potraktować jak dwójnik aktywny stanowiący rzeczywiste źródło napięciowe.

Powyższy wniosek jest znany pod nazwą Twierdzenia Thevenina.

3EKRAN_73

Twierdzenie Thevenina:

Każdy dwójnik aktywny można zastąpić źródłem rzeczywistym napięciowym o elementach E_T i R_T.

E_T- zwane napięciem Thevenina, jest to napięcie stanu jałowego na zaciskach dwójnika.

R_T- rezystancja Thevenina, jest to rezystancja jaką zmierzyłby omomierz przy zwarciu wszystkich SEM i rozwarciu SPM.

Komentarz-EKRAN_73

Twierdzenie Thevenina to zastąpienie dwójnika

aktywnego napięciowym źródłem rzeczywistym. Rezystancję R_T

obliczamy jako rezystancję zastępczą dwójnika pasywnego

powstałego po usunięciu źródeł przy czym po SEM gałąź zwie-

ramy a po SPM zostaje przerwana.

Biorąc pod uwagę równoważność rzeczywistych źródeł prądo-

wego i napięciowego każdy dwójnik aktywny można

zatem zastąpić także rzeczywistym źródłem prądowym.

Takie postępowanie nazywamy Twierdzeniem Nortona .

3EKRAN_74

Przykład 3.5

Obliczyć prąd płynący przez rezystor 6k stosując metodę zamiany źródeł i twierdzenie Thevenina.

Komentarz-EKRAN_74

Najpierw rzeczywiste źródło prądowe zostanie zamienione na rzeczywiste źródło napięciowe

zgodnie z formułą zawartą na ekranie 71 tj. E=IR . Rezystancja pozostaje ta sama.

3EKRAN_75

Obwód po zastąpieniu źródła prądowego napięciowym

Komentarz-EKRAN_75

Następnie wytniemy z obwodu lewą (w stosunku do rezystancji 6k jego część.

3EKRAN_76

Komentarz-EKRAN_76

Wycięty fragment obwodu zastępujemy źródłem napięciowym zgodnie z Tw. Thevenina.

3EKRAN_77

Komentarz-EKRAN_77

Oba obwody na ekranie są równoważne. Można powiedzieć, że gałąź 6V, 3k została przerzucona do środka.

Otrzymamy w ten sposób dwa źródła połączone równolegle i obciążone rezystancją 6k

3EKRAN_78

Komentarz-EKRAN_78

Układ równolegle połączonych żródeł znowu zastępujemy jednym źródłem Thevenina. Napięcie E_T można wyznaczyć następująco:

Ponieważ

Stąd

3EKRAN_79

Wzory obok rysunku stanowią uniwersalną formułę na połączenie równoległe dwóch źródeł napięciowych.

Komentarz-EKRAN_79

Formułę na E_T łatwo zapamiętać, zwracając uwagę, że w liczniku wpisujemy sumę iloczynów sił elektromotorycznych razy rezystancje w przeciwnych gałęziach. Wstawiając dane zadania otrzymamy:

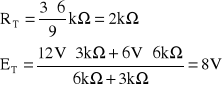
3EKRAN_80

Odpowiedź:

Ostatecznie cały obwód względem rezystancji 6k został sprowadzony do jednego źródła o parametrach 8V,2k. Stąd szukany prąd wynosi 1mA.

Komentarz-EKRAN_80

To zadanie można było rozwiązać zastępując od razu cały obwód ( po wycięciu rezystancji 6k) generatorem Thevenina. Przekonaj się, że otrzymasz identyczne rozwiązanie.

3EKRAN_80

Podsumowanie

W powyższej lekcji poznaliśmy dalsze metody pozwalające na analizę coraz bardziej złożonych obwodów. Należy jednak podkreślić, że większość z tych metod można stosować tylko w wypadku obwodów liniowych. Nie da się np. zwinąć obwodu z elementem nieliniowym gdyż nie będziemy znali jej rezystancji.

Również w przypadku zamiany źródeł prądowego na napięciowe trzeba pamiętać, że dotyczy to tylko źródeł rzeczywistych. Nie da się zamienić idealnej SPM na idealną SEM.

Istnieje pojęcie równoważności dwójników aktywnych z elementami sterowanymi. Niestety nie można analogicznie eliminować sterowanych SPM i SEM jak dotychczas dla obliczenia np. rezystancji Thevenina.

1

2

5

2

5

A

_V

1

5

2

5

2

5

R_W

E

G_W

I

A

G_W=0,5s

I=5A

A

G_W=0,5s

I=5A

V

G_W=0,5s

I=5A

I₀=0

V

R₁

R₂

R₃

1

2

3

_

R₁₂

R₂₃

R₃₁

1

2

3

_

R₁

R₂

R₃

1

2

3

R₁₂

R₂₃

R₃₁

1

2

3

2

R₃

R₂

R₁

1

3

R₃₁

R₂₃

R₁₂











A

A























1,697

A

10V

10V

R_z=1,697

R

E

I

U

R_w

V

I

G_W

G

U

I₀

R_W

E

0,5E

U(R)

R

E

U(I)

I

R₁

R₂

R₃

R₁>R₂>R₃

G_Z

I₀(R)

I

0,5I

R_W

R

G_W=0,5s

I=5A

5

1

_V

A

U_V=10V

I_A=5A





R_T

V

V

E_T

ETTT

R_T

10mA

2k

8V

4k

3k

6k

6V

10mA

2k

8V

4k

3k

6k

6V

20V

2k

8V

4k

3k

6k

6V

20V

2k

8V

4k

3k

6k

6V

20V

2k

8V

4k

E_T

E_T=12V

R_T=6k

6k

12V

6k

3k

6k

6V

12V

I

6k

6k

12V

6V

3k

I

6k

12V

6V

3k

E₁

E₂

R₁

R₂

E_T

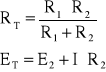
I

E₁

E₂

R₁

R₂

E_T

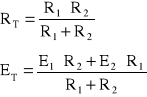
I

2k

8V

6k

---