PODSTAWOWE INFORMACJE O GAZACH

Pod koniec XVIII i w XIX wieku uczeni zaczęli badać własności fizyczne gazów i korelacje pomiędzy nimi, co doprowadziło do sformułowania kilku praw opisujących własności gazów. Oto one :

• Prawo Boyle'a-Mariotte'a

• Prawo Gay-Lussaca

• Prawo Charlesa

• Hipoteza Avogadro

• Prawo Daltona

W zasadzie prawa te powinny być Wam już znane z kursu fizyki (i to chyba nawet w liceum), niemniej jednak przypomnimy tu je w skrócie.

Prawo Boyle'a-Mariotte'a

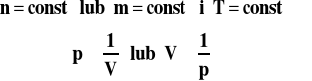
gdzie : n - liczba moli m - masa T - temperatura w skali Kelvina (termodynamicznej) p - ciśnienie V - objętość

Na rysunku 1 pokazana jest ilustracja graficzna tego prawa. Z matematycznego punktu widzenia każda linia dla danej, stałej temperatury to hiperbola. Linie te noszą nazwę izoterm. Ilustrują one przemianę izotermiczną gazu czyli przemianę przy stałej temperaturze.

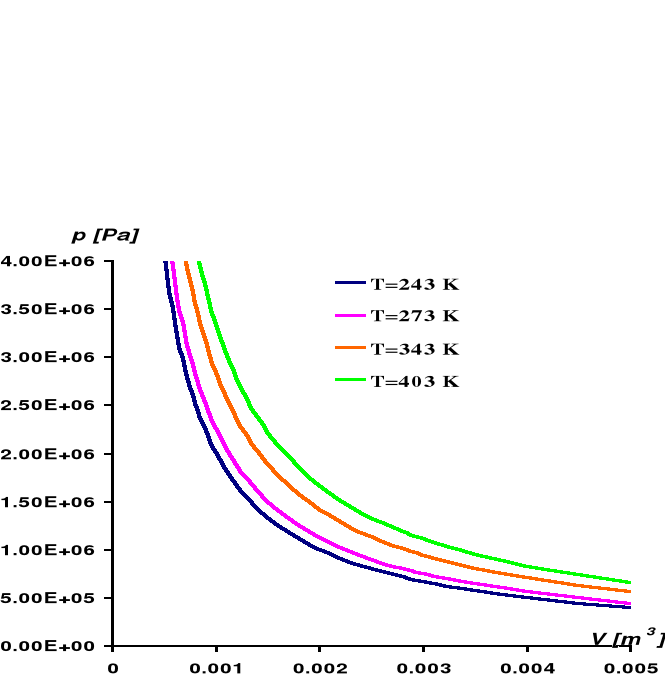
Rysunek 1. Ilustracja prawa Boyle'a - Mariotte'a dla 1 mola gazu w kilku różnych temperaturach.

Prawo Gay-Lussaca

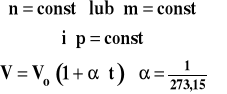
gdzie : t - temperatura w skali Celsjusza V_o - objętość gazu w temperaturze 0ºC  - współczynnik rozszerzalności termicznej gazu

Gdy temperaturę wyrazimy w skali Kelvina czyli jako T = t + 273,15 , to prawo Gay-Lussaca można zapisać następująco :

Na rysunku 2 pokazana jest ilustracja graficzna tego prawa. Każda linia na wykresie nosi nazwę izobary. Ilustrują one przemianę izobaryczną gazu czyli przemianę przy stałym ciśnieniu. Zauważmy, że gdy przeprowadzimy ekstrapolację do temperatury 0 kelwinów, to wszystkie izobary zbiegają się do jednego punktu, w którym objętość gazu wynosi zero.

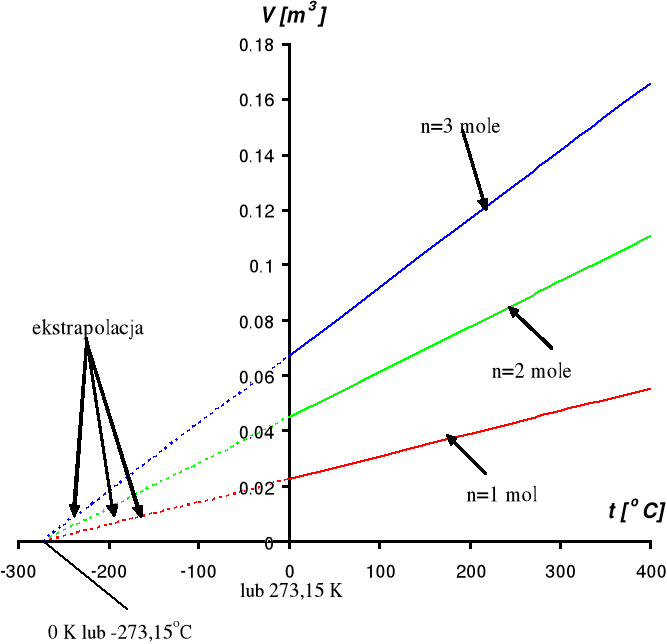
Rysunek 2. Ilustracja prawa Gay-Lussaca dla różnych ilości gazu pod ciśnieniem 1,013·10⁵ Pa.

Prawo Charlesa

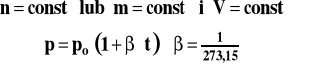
gdzie : t - temperatura w skali Celsjusza p_o - objętość gazu w temperaturze 0ºC  - współczynnik rozprężliwosci termicznej gazu

Gdy temperaturę wyrazimy w skali Kelvina czyli jako T = t + 273,15 , to prawo Charlesa można zapisać następująco :

Na rysunku 3 pokazana jest ilustracja graficzna tego prawa. Każda linia na wykresie nosi nazwę izochory. Ilustrują one przemianę izochoryczną gazu czyli przemianę w stałej objętości. Zauważmy, że gdy przeprowadzimy ekstrapolację do temperatury 0 kelwinów, to wszystkie izochory zbiegają się do jednego punktu, w którym ciśnienie gazu wynosi zero.

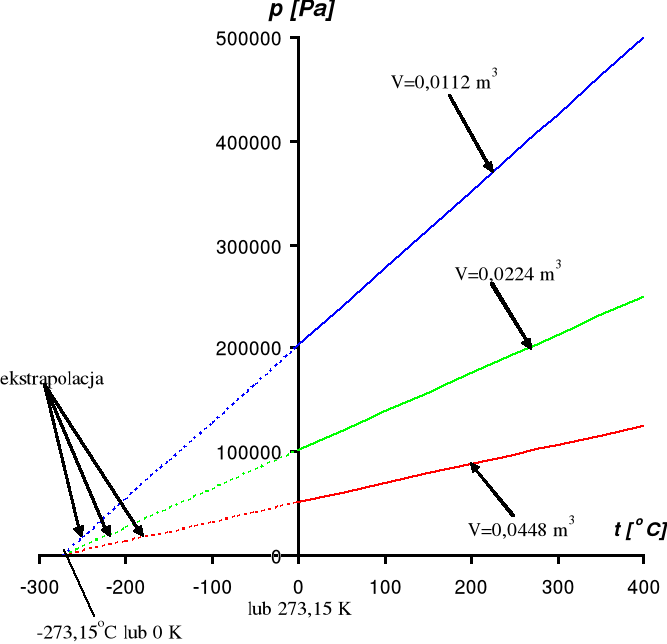
Rysunek 3. Ilustracja prawa Charlesa dla 1 mola gazu w różnych objętościach.

Hipoteza Avogadro

Z tej hipotezy wywodzi się pojęcie jednostki liczności materii i liczby Avogadro. 1 mol substancji (atomów, cząsteczek, jonów, cząstek elementarnych) to taka ilość, jaka jest liczba atomów zawartych w 12 gramach izotopu węgla ¹²C. Natomiast liczba Avogadro to ilość atomów, cząsteczek, jonów, cząstek elementarnych, jaka jest zawarta w 1 molu.

Z połączenia praw Boyle'a-Mariotte'a, Gay-Lussaca i Charlesa oraz hipotezy Avogadro otrzymuje się jedno równanie zwane równaniem stanu gazu doskonałego bądź równaniem Clapeyrona.

gdzie : R - stała gazowa; R = 8,314 J/mol·K

Gaz doskonały nie istnieje w rzeczywistości. Wszystkie gazy w swoim zachowaniu nie spełniają równania Clapeyrona. Są więc gazami rzeczywistymi. Własności gazów rzeczywistych stają się zbliżone do własności gazu doskonałego, gdy ich ciśnienie dąży do zera. Inaczej mówiąc im ciśnienie gazu niższe, tym lepiej spełnia on równanie Clapeyrona.

W chemii fizycznej definiujemy tzw. warunki normalne :

to = 0°C (T = 273,15 K)

po = 1,013·105 Pa

Objętość 1 mola gazu w tych warunkach wynosi

Vo = 22,4·10-3 m3/mol

Jeśli podstawimy te wartości do równania Clapeyrona dla 1 mola gazu, to możemy obliczyć wartość stałej gazowej.

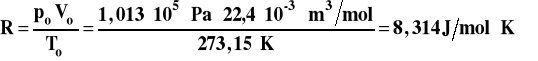
Dotychczas rozważaliśmy gaz jako całość nie wnikając w jego skład. Ale wiele gazów, z jakimi mamy w praktyce do czynienia to mieszaniny różnych składników, jak choćby otaczające nas powietrze będące mieszaniną tlenu, azotu, niewielkich ilości dwutlenku węgla, gazów szlachetnych i innych związków. Mieszaniny gazowe opisuje prawo Daltona.

Prawo Daltona

gdzie : P - ciśnienie całkowite mieszaniny gazów p_i - ciśnienie cząstkowe danego składnika

Jeśli wyrazimy ciśnienie cząstkowe i całkowite z równania stanu gazu doskonałego

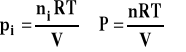
to :

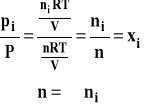
gdzie : n_i - liczba moli i-tego składnika n - sumaryczna liczba moli wszystkich składników x_i - ułamek molowy i-tego składnika w mieszaninie

Wobec tego ciśnienie cząstkowe składnika i-tego w mieszaninie można wyrazić jako :

Jest to bardzo istotny wniosek z prawa Daltona, który mówi, że ciśnienie cząstkowe składnika w mieszaninie można wyrazić jako iloczyn jego ułamka molowego w mieszaninie i ciśnienia całkowitego.

Znając eksperymentalne prawa opisujące zachowanie gazu doskonałego, zakładając, że składa się on z cząsteczek, sformułowano teorię kinetyczno-molekularną gazów.

Teoria kinetyczno molekularna gazów czyli model gazu doskonałego

Założenia :

• Wymiary cząsteczek są znikomo małe w porównaniu z odległościami pomiędzy nimi. Można traktować je jako punkty materialne.

• Cząsteczki są w ciągłym, chaotycznym ruchu.

• Cząsteczki nie oddziałują na siebie na odległość, jedynie dochodzi do doskonale elastycznych zderzeń.

W zderzeniach cząsteczki wymieniają między sobą energię kinetyczną i pęd, bez żadnych strat. Ponieważ nie ma oddziaływań pomiędzy cząsteczkami na odległość, to nie istnieją żadne siły przyciągające pomiędzy nimi, które mogłyby spowodować „sklejanie się” cząsteczek razem. Wobec tego z modelu wynika od razu, że gazu doskonałego nie można skroplić, gdyż w cieczy cząsteczki są utrzymane razem przez siły spójności działające na niewielką odległość pomiędzy nimi.

Załóżmy, że mamy 1 mol gazu zamknięty w sześciennym naczyniu o boku l. Zakładamy też, że cząsteczki o masie m poruszają się ruchem prostoliniowym ze średnią szybkością v. Prędkość cząsteczek, a więc i ich energia kinetyczna zależą od temperatury; rosną, gdy temperatura rośnie. Średnio pomiędzy równoległymi ściankami naczynia porusza się 1/3 wszystkich cząsteczek. Ciśnienie wywierane na ścianki naczynia powstaje dlatego, że cząsteczki gazu zderzając się ze ściankami oddając pęd. Zmiana pędu dla pojedynczej cząsteczki w zderzeniu ze ścianką naczynia wynosi 2mv. W czasie potrzebnym na przebycie przez cząsteczkę drogi l (od ścianki do ścianki naczynia) z jedną ścianką zderza się 1/6 wszystkich cząsteczek. Na podstawie tych założeń (wyprowadzenie pomijamy) można sformułować równanie wiążące ciśnie i objętość gazu z własnościami cząsteczek. Jest to prawo Boyle'a-Mariotte'a uzyskane na podstawie założeń teorii kinetyczno molekularnej gazu.

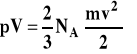
Energia kinetyczna pojedynczej cząsteczki wyraża się następująco :

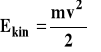
Wobec tego :

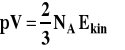
Dla 1 mola gazu można zapisać równanie Clapeyrona jako pV = RT. Wobec tego :

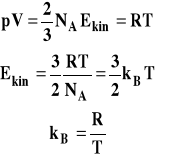
gdzie : k_B - stała Boltzmanna

Z otrzymanej zależności wynika, że energia kinetyczna cząsteczek gazu doskonałego zależy tylko od temperatury i jest do niej wprost proporcjonalna.

W przestrzeni trójwymiarowej prędkość cząsteczki, która jest wielkością wektorową, można rozłożyć na trzy składowe wzdłuż trzech kierunków przestrzeni (rysunek 4). Wobec tego całkowitą energię kinetyczną cząsteczki można rozłożyć też na trzy części odpowiadające udziałom dal ruchu wzdłuż kierunków x, y, z - E_kin,x, E_kin,y, E_kin,z.

Rysunek 4. Rozkład prędkości na składowe w przestrzeni trójwymiarowej.

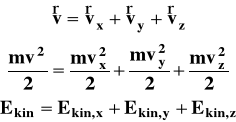
Średnio rozkład prędkości na trzy kierunki przestrzeni jest jednakowy, wobec tego średni udział energii kinetycznej przypadającej na dany kierunek to 1/3 całkowitej energii. Możliwości poruszania się cząsteczki w określonych kierunkach przestrzeni nazywamy stopniami swobody ruchu. Wynika stąd zasada ekwipartycji (równego podziału) energii.

Gazy rzeczywiste

Wszystkie gazy są gazami rzeczywistymi i nie spełniają równania stanu gazu doskonałego (Clapeyrona). Pierwsza podstawowa różnica pomiędzy gazami doskonałym a rzeczywistymi, to fakt, że wszystkie gazy rzeczywiste w odpowiednio niskiej temperaturze ulegają skropleniu, a gaz doskonały nie.

Aby opisać zachowanie gazu rzeczywistego wprowadzono do równania stanu gazu współczynnik korekcyjny, zwany współczynnikiem ściśliwości z. Nazwa tego współczynnika nie jest właściwie dobrana, gdyż nie ma on nic wspólnego ze ściśliwością gazu, ale przyjęła się w literaturze.

Wartość współczynnika z jest dobierana doświadczalnie i zależy od rodzaju gazu oraz temperatury i ciśnienia. Na rysunku 5 przedstawiono schematycznie typową zależność tego współczynnika od ciśnienia w kilku temperaturach.

Rysunek 5. Przykładowa zależność współczynnika ściśliwości od ciśnienia kilku temperaturach.

Jak widać, im wyższa temperatura tym mniejsze są odchylenia w zachowaniu gazu rzeczywistego od doskonałości. Dla gazu doskonałego współczynnik ściśliwości wynosi zawsze 1.Gdy ciśnienie gazu rzeczywistego dąży do zera, współczynnik ściśliwości dąży do 1 czyli własności gazu rzeczywistego dążą do własności gazu doskonałego.

Równanie opisujące zachowanie gazu rzeczywistego powstałe przez modyfikację równania Clapeyrona jest równaniem czysto empirycznym. Aby stworzyć równanie opisujące zachowanie gazu rzeczywistego na podstawie modelu, musimy zmodyfikować model gazu. Do gazu rzeczywistego nie można zastosować modelu opisującego gaz doskonały.

• Cząsteczki gazu rzeczywistego posiadają pewną objętość własną, której nie można zaniedbać.

• Cząsteczki gazu rzeczywistego oddziaływają ze sobą na odległość.

Oddziaływania międzycząsteczkowe mają charakter odpychający i przyciągający. Gdy odległość pomiędzy cząsteczkami jest niewielka i energia termiczna cząsteczek jest też stosunkowo mała, zderzenia pomiędzy nimi nie są elastyczne. Przeważają oddziaływania przyciągające i cząsteczki „sklejają się” z sobą, a gaz się skrapla.

Równanie opisujące gaz rzeczywisty musi uwzględniać objętość własną cząsteczek i oddziaływania międzycząsteczkowe (przyciąganie cząsteczek). Czyli w równaniu stanu gazu musimy od objętości gazu odjąć najmniejszą objętość, jaką mogą zająć cząsteczki gazu najgęściej upakowane, a do ciśnienia dodać wkład spowodowany przez siły przyciągające pomiędzy cząsteczkami. W ten sposób powstało półempiryczne równanie van der Waalsa.

Równanie van der Waalsa dla jednego mola gazu

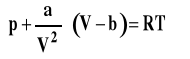
Równanie van der Waalsa dla n moli gazu

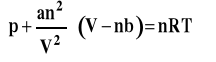
gdzie : a, b - stałe charakterystyczne dla danego gazu, niezależne od temperatury a - stała związana z oddziaływaniami międzycząsteczkowymi (przyciąganiem) b - stała związana z objętością własną cząsteczek

Określenie „półempiryczne” oznacza, że równanie to powstało na drodze pewnego modelu i rozumowania teoretycznego, ale współczynniki a i b w nim dobierane są w oparciu doświadczenie. Przyjrzyjmy się teraz nieco bliżej tym współczynnikom.

Współczynnik b oznacza objętość, jaką mogą zająć najgęściej upakowane cząsteczki gazu (rysunek 6).

Rysunek 6. Najgęstsze upakowanie cząsteczek gazu (pokazane na płaszczyźnie)

Cząsteczki gazu możemy potraktować jako sztywne kulki o promieniu r. Objętość pojedynczej cząsteczki wyrazi się jako :

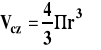
Można wykazać na drodze rozważań geometrycznych, że kule można ułożyć najgęściej w objętości cztery razy większej niż objętość własna tych kul. Wobec tego 1 mol cząsteczek gazu zajmie objętość :

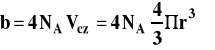
Znając stałą b w równaniu van der Waalsa można obliczyć promień cząsteczki gazu :

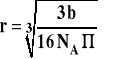
Stała a związana jest z oddziaływaniami pomiędzy cząsteczkami, które mogą mieć charakter przyciągający i odpychający. Energię oddziaływań pomiędzy dwiema cząsteczkami można opisać równaniem :

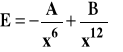
gdzie : A, B - pewne stałe (A - oddziaływania przyciągające, B - odpychające) x - odległość pomiędzy cząsteczkami

Oddziaływanie odpychające są istotne tylko przy bardzo małych odległościach pomiędzy cząsteczkami, gdy praktycznie one stykają się ze sobą (rysunek 7). Wobec tego można je zaniedbać i wyrazić energie oddziaływań międzycząsteczkowych jako :

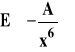
Rysunek 7. Zależność energii oddziaływań dwu cząsteczek w funkcji odległości pomiędzy nimi.

Można wykazać, że w efekcie oddziaływania przyciągające dają dodatkowy wkład do ciśnienia, którego wartość jest odwrotnie proporcjonalna do objętości podniesionej do kwadratu czyli do ciśnienia dodajemy a/V².

Jak wiadomo zasadniczą różnicą pomiędzy gazem doskonałym a rzeczywistym jest fakt, że ten ostatni ulega skropleniu. Temperatura, w której zachodzi skraplanie gazu, zależy od ciśnienia. Temperatura skraplanie rośnie wraz ze wzrostem ciśnienia. W danej stałej temperaturze, im jest ona wyższa, tym wyższego ciśnienia należy użyć, aby skroplić gaz. Ale gazy rzeczywiste ulegają skropleniu nie w każdej dowolnej temperaturze. Istnieje pewna graniczna temperatura, zwana temperaturą krytyczną, powyżej której gazu nigdy nie można skroplić. W temperaturze krytycznej zanika różnica pomiędzy gazem i cieczą. Natomiast poniżej tej temperatury gaz można skroplić.

Na rysunku 8 przedstawiono izotermy dla gazu rzeczywistego wynikające z równania van der Waalsa.

Rysumek 8. Izotermy dla gazu rzeczywistego.

W wysokich temperaturach przebieg izotermy jest bardzo podobny do izotermy gazu doskonałego (temperatura T₆ na rysunku 8). W miarę obniżania temperatury kształt izotermy zaczyna odbiegać od hiperboli (temperatura T₅). W temperaturze krytycznej T₄ (T_kr) w punkcie krytycznym na izotermie pojawia się poziomy punkt przegięcia. Ciśnienie można wyrazić w funkcji objętości z równania van der Waalsa następująco :

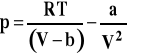
Z matematyki wiadomo, że jeśli na krzywej mamy poziomy punkt przegięcia, to wartość pierwszej i drugiej pochodnej w tym punkcie są równe zero, czyli :

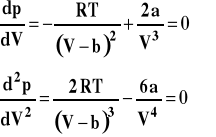
Z tych zależności można wyrazić parametry a i b w równaniu van der Waalsa przez wielkości opisujące punkt krytyczny czyli ciśnienie krytyczne p_kr, temperaturę w punkcie krytycznym T_kr i molową objętość gazu w punkcie krytycznym V_kr.

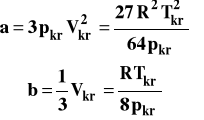
Parametry opisujące punkt krytyczny można wyznaczyć w sposób doświadczalny, a więc dalej w oparciu o podane zależności można wyznaczyć stałe a i b oraz promień cząsteczki gazowej.

Poniżej temperatury krytycznej gaz ulega skropleniu, gdy ciśnienie osiągnie odpowiednią wartość. Równanie van der Waalsa ze względu na objętość jest równaniem trzeciego stopnia. Wobec tego dla temperatur poniżej krytycznej na izotermie pojawia się lokalne minimum i lokalne maksimum. Taki przebieg izotermy jest w rzeczywistości niemożliwy, gdyż z przebiegu krzywej od minimum do maksimum wynika, że wraz ze wzrostem ciśnienia objętość też by rosła, a tak nigdy się nie dzieje. Zawsze dla każdej substancji w dowolnym stanie skupienia, gdy ciśnienie rośnie, objętość maleje. Co wobec tego się dzieje i jak w rzeczywistości zależy ciśnienie od objętości ? Prześledźmy to na izotermie T₁ (najniższa jasno niebieska linia na rysunku 8). W miarę sprężania gazu ciśnienie nieznacznie rośnie, aż w punkcie B rozpoczyna się skraplanie i pojawia się pierwsza kropla cieczy. Dalej w miarę zmniejszania objętości ilość cieczy zwiększa się, a maleje ilość gazu, aż w punkcie A znika ostatni pęcherzyk gazu czyli skraplanie gazu kończy się. W obszarze od A do B ciśnienie jest stałe, nie zależy od objętości układu. Mamy do czynienia z równowagą pomiędzy gazem i cieczą, zmieniają się tylko ilości poszczególnych faz. Gdy zniknie ostatni pęcherzyk gazu, to ciśnienie zaczyna gwałtownie rosnąć w miarę zmniejszania objętości. Jest to zrozumiałe, gdyż w cieczy mamy ciasno upakowane cząsteczki i sprężanie cieczy musi prowadzić do ściskania samych cząsteczek. Na rysunku 8 grubą przerywaną linią połączono punkty na izotermach, w których rozpoczyna się i kończy skraplanie. Poniżej tej linii mamy obszar współistnienia gazu i cieczy. Na rysunku 9 przedstawiono obszary występowania gazu i cieczy. Pokazuje on w jakich zakresach ciśnienia i objętości istnieje gaz lub ciecz, a gdzie jest obszar ich współistnienia.

Rysunek 9. Obszary współistnienia gazu i cieczy.

[Wpisz tekst]

[Wpisz tekst]

Dla pewnej stałej ilości gazu w stałej temperaturze ciśnienie jest odwrotnie proporcjonalne do objętości czyli iloczyn ciśnienia i objętości jest stały.

izoterma

Dla pewnej stałej ilości gazu pod stałym ciśnieniem objętość jest liniową funkcją temperatury.

Dla pewnej stałej ilości gazu pod stałym ciśnieniem objętość jest wprost proporcjonalna do temperatury w skali Kelvina.

Dla pewnej stałej ilości gazu w stałej objętości ciśnienie jest liniową funkcją temperatury.

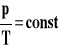
Dla pewnej stałej ilości gazu w stałej objętości ciśnienie jest wprost proporcjonalne do temperatury w skali Kelvina.

Jeśli mamy różne gazy w tej samej objętości i temperaturze i pod tym samym ciśnieniem, to zawierają one te same ilości cząsteczek.

Gaz, który spełnia równanie Clapeyrona nazywamy gazem doskonałym.

Ciśnienie całkowite mieszaniny gazów jest sumą ciśnień cząstkowych poszczególnych składników. Ciśnienie cząstkowe danego składnika gazowego, to ciśnienie jakie wywierałby, gdyby sam znajdował się w danych warunkach.

y, v_y

v

z, v_z

x, v_x

Na każdy stopień swobody ruchu cząsteczki przypada energia wynosząca ½ k_BT

p

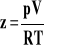
T₂

T₃

T₁ < T₂ < T₃

T₁

1

gaz doskonały

z = 1

odległość pomiędzy cząsteczkami

E

przewaga przyciągania

przewaga odpychania

0

A

B

---