Wykład 2. 6 X 2004

PRZYSPIESZENIE I JEGO SKŁADOWE W UKŁADZIE KARTEZJAŃSKIM

Wektor przyspieszenia w układzie kartezjańskim - zapis w formalizmie wersorowym.

Przyspieszenie można przedstawić w układzie kartezjańskim jako wektor o trzech współrzędnych:

a = a_x i + a_y j + a_z k

Składowe: a_xi, a_yj, a_zk są wektorami powstałymi przez prostokątne rzutowanie wektora a na osie OX, OY oraz OZ.

Zachodzą związki:

a_x =
, a_y =
, a_z =
, które wynikają z definicji wektora przyspieszenia jako pochodnej wektora prędkości oraz przedstawienia wektora prędkości w formie zapisu z użyciem wersorów: v = v_x i + v_y j + v_z k

PRZYSPIESZENIE STYCZNE I NORMALNE.

Układ współrzędnych naturalny - definicja.

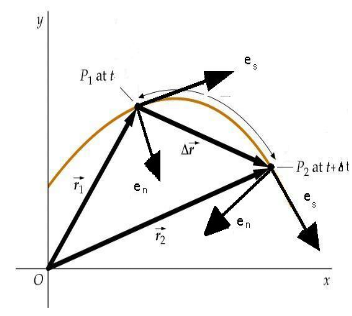
Załóżmy, że cząstka porusza się po torze krzywoliniowym. W chwili t znajduje się ona w punkcie toru P₁ a w chwili (t +t) w punkcie P₂.

Definiujemy w punkcie toru P₁ wersor styczny do toru e_s oraz w kierunku prostopadłym do toru wersor normalny e_n. Wersory te przemieszczają się wraz z cząstką wzdłuż toru ruchu i w przypadku toru krzywoliniowego będą zmieniały swój kierunek.

Porównaj kierunki wersorów na rysunku w chwili t w punkcie P₁ i w chwili (t +t) w punkcie P₂.

Prędkość w układzie naturalnym.

Prędkość w układzie naturalnym można zapisać bardzo prosto: v = v(t) e_s. Wyrażony jest w ten sposób fakt, że wektor prędkości jest styczny do toru.

Przyspieszenie w układzie naturalnym. Pokazanie, że: a=
e_s +
e_n

Zgodnie z definicją przyspieszenia: a=
=

=
e_s + v
. Przy wersorze stycznym mamy wielkość
, która informuje jak zmienia się wartość wektora prędkości. Dla uzyskania pełnej zależności dla przyspieszenia należy przeanalizować pochodną czasową wersora stycznego.

Obliczenie pochodnej wersora stycznego po czasie:
=
e_n

Na rysunku obok pokazane są sprowadzone do wspólnego punktu wersory styczne do toru w chwili t (w punkcie toru P₁) oraz t+dt . Kąt jaki one tworzą wynosi d, można więc znaleźć długość przyrostu wersora stycznego:

=
d d, bo długość wersora wynosi jeden. Pozostaje jeszcze znaleźć kierunek przyrostu wersora de_s.

Dowód, że
jest prostopadłe do e_s.

Biorąc iloczyn skalarny wersorów
=1. Obliczając pochodną po czasie obu stron otrzymamy dla strony lewej:

oraz dla prawej:

. Czyli łącząc te związki mamy:
. Ponieważ ani długość wersora ani jego pochodna nie są równe zeru, to musi zachodzić sytuacja, że wersor styczny jest prostopadły do swojej pochodej czasowej.

Mamy więc znaleziony kierunek przyrostu wersora stycznego. Jest on zgodny z kierunkiem wersora normalnego, czyli:

de_s=d e_n. Stąd mamy związek dla pochodnej wersora stycznego:
=
e_n.

Obliczenie a_s i a_n oraz ich interpretacja fizyczna.

Wracając do wzoru opisującego przyspieszenie w układzie naturalnym i wstawiając otrzymany wynik dla pochodnej wersora stycznego otrzymamy:

a=
=
e_s + v
e_n.

Kąt d jest również kątem jaki tworzą dwie proste prostopadłe do toru w kolejnych punktach toru (P₁ i P₂) odpowiadających położeniu cząstki w czasie t i czasie t+dt. Proste te przecinając się tworzą odcinki o długościach równych promieniowi krzywizny oznaczanemu przezρ. Ponieważ łuk P₁P₂ ma długość ds, to można zapisać związek ds = ρ d, czyli
.

Ponieważ wartość prędkości v =
, to
. Otrzymujemy więc wynik:

a=
=
e_s +
e_n.

UWAGA - Wnioski końcowe. To jest najważniejsze !!

Wartość przyspieszenia stycznego
określa nam jak zmienia się wartość prędkości w ruchu, natomiast wartość przyspieszenia normalnego
określa jaka jest krzywizna toru czyli zawiera informację o zmianie kierunku wektora prędkości.

• Problem: Kiedy v=const, a przyspieszenie całkowite a
  0? [odpowiedź na końcu tekstu]

Klasyfikacja ruchów ze względu na przyspieszenie.

Przyspieszenie: a=
=
e_s +
e_n = a _s e_s +a _n e_n

• kierunek prędkości stały, wartość stała - ruch prostoliniowy jednostajny.

a _s= 0, a _n=0, ρ

• kierunek prędkości stały, wartość zmienna - ruch prostoliniowy zmienny

a _s niezerowe, a _n= 0, ρ

• kierunek prędkości zmienny, wartość stała - ruch krzywoliniowy po okręgu

a _s = 0, a _n stałe i różne od zera, ρR i stałe równe promieniowi okręgu.

• kierunek prędkości zmienny, wartość zmienna - ruch krzywoliniowy zmienny

a _s zmienne, a _n zmienne, ρ zmienne.

Sprawdź czy to rozumiesz. Sam(a) spróbuj opisać w ten sposób różne znane Ci z życia codziennego lub z kursu fizyki szkolnej przykłady ruchów.

ŚREDNIA PRĘDKOŚĆ I ŚREDNIE RZYSPIESZENIE.

Definicja prędkości średniej i przyspieszenia średniego.

Prędkość średnia określona jest jako iloraz wektora przemieszczenia, które nastąpiło w skończonym czasie t do wartości tego przedziału czasu t:

.

Podobnie przyspieszenie średnie jest ilorazem zmiany wektora prędkości v, która nastąpiła w skończonym czasie t do wartości tego przedziału czasu t:

. Są to wielkości wektorowe.

TRANSFORMACJA GALILEUSZA.

Opis ruchu punktu P (DOWOLNY RUCH OBIEKTU - NA PRZYKŁAD MUCHY) w układach inercjalnych U oraz U^' - transformacja Galileusza.

Jeśli układ U^' zwany dalej primowanym porusza się ze stałą prędkością v_u tak, że osie OX oraz OX' są równoległe oraz w chwili t=0 punkty O i O' pokrywały się, wtedy:

OO' = v_u t

Oraz współrzędna muchy P:

x(t) = x'(t) + v_u t

Stąd składowe prędkości muchy na osie ox oraz ox^' spełniają relację:

v_x (t)= v_x' (t) + v_u

oraz podobnie:

a_x (t) = a_x' (t)

(pomyśl co stało się z pochodną po czasie v_u ?)

Mnożąc obie strony przez masę cząstki otrzymamy wniosek, że także siły działające na obiekt (muchę) są równe w obu układach odniesienia:

F_x(t) = F_x' (t)

UWAGA:

Zauważ, że nie ma tu nigdzie mowy o siłach działających na układ xOy czy x'O'y'. Pomyśl dlaczego tak jest. Pomocne będzie pytanie: "Jaką masę ma układ U oraz U'?"

UKŁADY INERCJALNE.

Analizując ruch cząstki w układzie poruszającym się ruchem jednostajnym i prostoliniowym względem obserwatora nieruchomego otrzymamy równanie opisujące siłę na nią działającą identyczne jak dla układu nieruchomego. Prawa dynamiki Newtona opisują więc poprawnie ruch w każdym układzie inercjalnym.

Można sformułować zasadę względności Galileusza.

Wszystkie prawa mechaniki wyglądają identycznie we wszystkich inercjalnych układach odniesienia.

Fizycy mówią: Prawa mechaniki są niezmiennicze ze względu na wybór inercjalnego układu odniesienia.

Uwaga na marginesie:

Okaże się, że transformacja Galileusza jest jednak tylko przybliżeniem. Dla dużych prędkości układu inercjalnego zaczynają się kłopoty podczas używania przepisu na dodawanie prędkości takiego jak powyżej używany i musimy go zmodyfikować. O tym jak to zrobić dowiecie się jeszcze w tym semestrze.

Pojęcie układu inercjalnego. Sens tego sformułowania. (patrz wykład)

Zasada bezwładności - pierwsza zasada dynamiki

Poniżej podane jest sformułowanie pierwszej zasady dynamiki często spotykane w podręcznikach do Fizyki do szkół średnich:

Jeśli na ciało nie działa żadna siła lub działają siły równoważące się to pozostaje ono w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

Nie jest ona błędna, ale nie wynika z niej jasno, co konkretnie dzieje się na przykład z obiektem, na który działają siły równoważące się. Według powyższego sformułowania jest nieruchomy albo porusza się ruchem jednostajnym, a to nie jest rzecz do wyboru.

Sformułowanie Newtona jest następujące:

Każde ciało pozostaje w spoczynku albo w stanie ruchu jednostajnego prostoliniowego, dopóki oddziaływanie ze strony innych ciał nie zmieni tego stanu.

Widać, że obiekt robi dalej to co robił dopóki nie będzie czegoś (oddziaływania ze strony innych ciał) co ten stan zmieni. Czyli jeśli pozostawał w spoczynku to nadal tak będzie, a gdy poruszał się ruchem jednostajnym prostoliniowym to nadal tak będzie robił aż do czasu gdy pojawi się działająca na niego niezrównoważona siła.

Matematyczny zapis dla obiektu o masie m: v=const, czyli a = 0 lub mv = const.

Masa zapewnia tu ruch ciała pomimo braku siły (jeśli przedtem się ono poruszało).

Pierwszą zasadę dynamiki wyróżniamy ponieważ dzięki niej możemy wyróżnić grupę inercjalnych układów odniesienia.

Można pierwszą zasadę dynamiki sformułować także następująco:

Obiekt obserwowany w inercjalnym układzie odniesienia nie zmieni swego stanu samoistnie. Zmieni go tylko wtedy, gdy będzie na niego działała jakaś różna od zera wypadkowa siła.

PRZEDMIOT DYNAMIKI

Dynamika opisuje ruch obiektów analizując jego przyczyny. Bada więc siły z jakimi oddziałują na siebie elementy danego układu oraz działające na elementy układu siły zewnętrzne i poprzez sformułowanie równań ruchu daje nam narzędzie do obliczenia toru ruchu, prędkości i przyspieszeń poszczególnych elementów składowych tego układu. Można historycznie podzielić dynamikę na nierelatywistyczną (v<<c) i relatywistyczną (prędkości bliskie prędkości światła c).

Zasady dynamiki. - zostały sformułowane przez Isaaca Newtona. Zostały sformułowane na podstawie obserwacji. Z ich przyjęcia wynika szereg wniosków: np. prawo zachowania pędu, energii mechanicznej, zasada względności Galileusza.

Pojęcie masy bezwładnej - Jest to wielkość skalarna charakteryzująca dane ciało niezależnie od położenia względem innych ciał. Jest ona miarą bezwładności ciała. Proszę sobie przypomnieć co dzieje się jeśli taka sama stała siła będzie działała na dwa ciała i wywoła różne skutki w postaci innych przyspieszeń. Ciało o mniejszym przyspieszeniu będzie miało większą masę.

Pojęcie siły - Jest to wielkość wektorowa. Jest ona przyczyną zmiany ruchu (v - prędkości ciała) lub odkształcenia (w przypadku obiektu rozciągłego-bryły).

(Są tu pewne powtórzenia dla zachowania kompletności zasad dynamiki 1,2 i 3)

Zasada bezwładności - pierwsza zasada dynamiki

Poniżej podane jest sformułowanie pierwszej zasady dynamiki często spotykane w podręcznikach do Fizyki do szkół średnich:

Jeśli na ciało nie działa żadna siła lub działają siły równoważące się to pozostaje ono w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

Nie jest ona błędna, ale nie wynika z niej jasno, co konkretnie dzieje się na przykład z obiektem, na który działają siły równoważące się. Według powyższego sformułowania jest nieruchomy albo porusza się ruchem jednostajnym, a to nie jest rzecz do wyboru.

Sformułowanie przypisywane Newtonowi jest następujące:

Każde ciało pozostaje w spoczynku albo w stanie ruchu jednostajnego prostoliniowego, dopóki oddziaływanie ze strony innych ciał nie zmieni tego stanu.

Widać, że obiekt robi dalej to co robił dopóki nie będzie czegoś (oddziaływania ze strony innych ciał) co ten stan zmieni. Czyli jeśli pozostawał w spoczynku to nadal tak będzie, a gdy poruszał się ruchem jednostajnym prostoliniowym to nadal tak będzie robił aż do czasu gdy pojawi się działająca na niego niezrównoważona siła.

Matematyczny zapis dla obiektu o masie m: v=const, czyli a = 0 lub mv = const.

Masa zapewnia tu ruch ciała pomimo braku siły (jeśli przedtem się ono poruszało).

Pierwszą zasadę dynamiki wyróżniamy ponieważ dzięki niej możemy wyróżnić grupę inercjalnych układów odniesienia.

Można pierwszą zasadę dynamiki sformułować także następująco:

Obiekt obserwowany w inercjalnym układzie odniesienia nie zmieni swego stanu samoistnie. Zmieni go tylko wtedy, gdy będzie na niego działała jakaś różna od zera wypadkowa siła.

Druga zasada dynamiki. Masa bezwładna.

Jeśli na ciało działa stała niezrównoważona siła to porusza się ono ruchem jednostajnie przyspieszonym, z przyspieszeniem wprost proporcjonalnym do wartości tej siły.

Działając taką samą siłą na różne obiekty możemy stwierdzić, że ich przyspieszenia się różnią. Wprowadzając wielkość skalarną m - masę można powiedzieć, że obiekt o większej masie trudniej przyspieszyć. Masa jest miarą bezwładności ciała.

Zasada zachowania pędu dla układu n ciał - wynika z drugiej zasady dynamiki Newtona. Jeśli wypadkowa siła zewnętrzna F = 0 = ma to przyspieszenie środka masy układu jest wektorem zerowym i stąd pęd całkowity (liczony jako suma wektorów) układu n ciał jest wektorem stałym.

Trzecia zasada dynamiki.

Konsekwencją jej stosowania jest założenie nieskończenie szybkiego rozchodzenia się impulsów. Zakładamy, że każdej akcji towarzyszy natychmiastowa reakcja. Równa co do wartości ale o przeciwnym zwrocie.

• Problem: “Paradoks” konia i wozu ciągnących się z takimi samymi siłami. Czemu to się porusza? Zawsze siły te są przyłożone do różnych ciał.

Patrz wykład: Siły zewnętrzne i wewnętrzne dla rozpatrywanego układu.

Równania ruchu - przykłady. (zagadnienie na ćwiczenia)

Odpowiedź : Kiedy v=const, a przyspieszenie całkowite a
0?

Jest to ruch po okręgu. Przyspieszenie styczne wynosi zero, bo prędkość ma stałą wartość, natomiast normalne jest różne od zera ponieważ tor jest krzywoliniowy i promień krzywizny jest tu stały i równy promieniowi okręgu.

---