SPRAWOZDANIE Z ĆWICZENIA LABORATORYJNEGO NR 9

Wykonał: Wojciech Węgrecki

Grupa: I9G2S1

Treść zadania:

Ćwiczenie obejmuje zadania:

1. Zaprojektowanie filtru FIR dolnoprzepustowego

2. Dokonanie filtracji sygnału dźwiękowego metodami:

• z definicji splotu;

• korzystając z DFT;

• wykorzystując funkcję conv;

1. Wyświetlenie charakterystyki amplitudowej filtru.

2. Zbadać wpływ rzędu filtru na jego jakość.

3. Zaprojektowanie filtru FIR pasmowo przepustowego

4. Dokonanie filtracji sygnału dźwiękowego metodami:

• z definicji splotu;

• korzystając z DFT;

• wykorzystując funkcję conv;

1. Wyświetlenie charakterystyki amplitudowej filtru.

2. Zbadać wpływ rzędu filtru na jego jakość.

Wykonanie zadania:

9.1

Zadanie polegało na zaprojektowaniu filtru FIR dolnoprzepustowego, który opisany jest wzorem.

Wykonałem to za pomocą kodu:

fc=2000;

s1=fft(s);

h_dft=fft(h);

for i=1:length(h_dft)

w(i)=h(i);

end

for i=(length(h_dft)+1):length(s1)

w(i)=0;

end;

h_dft=fft(w);

for i=1:length(s1)

l(i)=s1(i)*h_dft(i);

end;

9.2, 9.3

Należało dokonać filtracji sygnału dźwiękowego różnymi metodami oraz należało wyświetlić charakterystyki widmowe i częstotliwościowe dla każdej metody:

• z definicji splotu:

Dokonałem tego za pomocą:

%z definiciji splotu

dlugosc_s=length(s);

dlugosc_h=length(h);

for i=1:dlugosc_s

for j=1:dlugosc_h

t(i,j+i+1)=s(i)*h(j);

end;

end;

for i=1:dlugosc_s+dlugosc_h-1

y(i)=sum(t(:,i));

end;

figure(2);

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

stem(czestotliwosc,abs(fft(y)));

title('Widmo amplitudowe filtru dolnoprzepustowego (z definicji)');

figure(3);

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

plot(czestotliwosc,abs(fft(y)));

title('Charakterystyka amplitudowa filtru dolnoprzepustowego (z definicji)')

rys. 1 Widmo amplitudowe filtru dolnoprzepustowego (z definicji)

rys. 2 Charakterystyka amplitudowa filtru dolnoprzepustowego (z definicji)

• korzystając z DFT;

Do wykonania tego zadania wykorzystałem właśności:

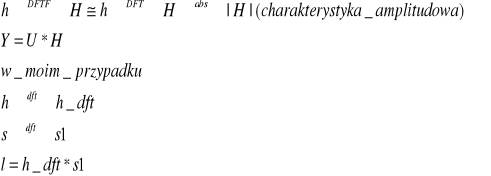
Powyższe własności realizuje kod:

s1=fft(s);

w=zeros(length(s1),1);

h_dft=fft(h);

l=zeros(length(s1),1);

for i=1:length(h_dft)

w(i)=h(i);

end

for i=(length(h_dft)+1):length(s1)

w(i)=0;

end;

h_dft=fft(w);

for i=1:length(s1)

l(i)=s1(i)*h_dft(i);

end;

[roz_h_dft,cos]=size(h_dft);%wyznaczanie rozmiaru sygnału h_dft

czestotliwosc=0:(fs/roz_h_dft):(fs*(roz_h_dft-1)/roz_h_dft);

figure(4)

stem(czestotliwosc,abs(l));

title('Widmo amplitudowe filtru dolnoprzepustowego (za pomoca dft)');

figure(5);

plot(czestotliwosc,abs(h_dft));

title('Charakterystyka amplitudowa filtru dolnoprzepustowego (za pomoca dft)')

rys. 3 Widmo amplitudowe filtru dolnoprzepustowego (z DFT)

rys. 4 Charakterystyka amplitudowa filtru dolnoprzepustowego (z DFT)

• wykorzystując funkcję conv;

W tym przypadku wystarczyło użyć wbudowanej funkcji środowiska MATLAB i wyświetlić odpowiednie wykresy, realizuje to skrypt:

y=conv(s,h);

[n,x]=size(y);

czestotliwosc=0:(fs/n):(fs*(n-1)/n);

figure(6)

A=fft(y);

stem(czestotliwosc,abs(A));

title('Widmo amplitudowe filtru dolnoprzepustowego (conv)');

figure(7);

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

plot(czestotliwosc,abs(fft(h)));

title('Charakterystyka amplitudowa filtru dolnoprzepustowego (conv)')

wavwrite(y,fs,'dzwiek_po_filtracji_dolno');

rys. 5 Widmo amplitudowe filtru dolnoprzepustowego (conv)

rys. 6 Charakterystyka amplitudowa filtru dolnoprzepustowego (conv)

9.4

Należało zbadać wpływ rzędu na jakoś filtru, aby to wykonać zamieniałem wartości N z zadania 9.2 i kolejno wyświetlałem wykresy dla różnych wartości.

rys. 7 N=101

rys. 8 N=301

rys. 9 N=501

Jakość tych wykresów określamy za pomocą stromizny jaka na nim występuje. Im ona jest większa, tym wykres jest lepszej jakości. Na pierwszy rzut oka od razu widać, że jakość tych wykresów się poprawia. Ze zwiększaniem rzędu N wykres był coraz bardziej stromy i występował coraz bliżej naszej wartości fc=2000Hz.PASMOPRZEPUSTOWY

9.5

Zadanie polegało na zaprojektowaniu filtru FIR pasmooprzepustowego, który opisany jest wzorem.

Wykonałem to za pomocą kodu:

fc1=1000;

fc2=2000;%czestotliwsc graniczna

N=301; %rzad filtru

%z definicji splotu

% projektowanie filtru

ni_c1=2*pi*fc1/fs;

ni_c2=2*pi*fc2/fs;

przedzial=ceil(N/2);

h1(przedzial)=ni_c1/pi;

for k=1:przedzial-1

h1(przedzial+k)=sin(k*ni_c1)/(pi*k);

h1(przedzial-k)=sin(k*ni_c1)/(pi*k);

end;

przedzial=ceil(N/2);

h2(przedzial)=ni_c2/pi;

for k=1:przedzial-1

h2(przedzial+k)=sin(k*ni_c2)/(pi*k);

h2(przedzial-k)=sin(k*ni_c2)/(pi*k);

end;

h=h2-h1;

9.6, 9.7

Należało dokonać filtracji sygnału dźwiękowego różnymi metodami oraz należało wyświetlić charakterystyki widmowe i częstotliwościowe dla każdej metody:

• z definicji splotu:

Dokonałem tego za pomocą:

%z definiciji splotu

for i=1:dlugosc_s

for j=1:dlugosc_h

t(i,j+i+1)=s(i)*h(j);

end;

end;

for i=1:dlugosc_s+dlugosc_h-1

y(i)=sum(t(:,i));

end;

figure(8)

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

stem(czestotliwosc,abs(fft(y)));

title('Widmo amplitudowe filtru pasmoprzepustowego (z definicji)')

figure(9)

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

plot(czestotliwosc,abs(fft(y)));

title('Charakterystyka amplitudowa filtru pasmoprzepustowego (definicja)')

rys. 10 Widmo amplitudowe filtru pasmo przepustowego (z definicji)

rys. 11 Charakterystyka amplitudowa filtru pasmo przepustowego (z definicji)

• korzystając z DFT;

Do wykonania tego zadania wykorzystałem własności:

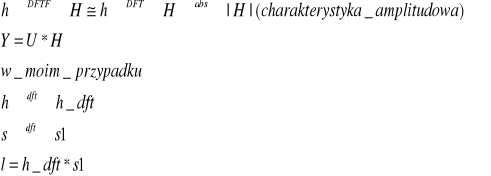
Powyższe własności realizuje kod:

s1=fft(s);

w=zeros(length(s1),1);

h_dft=fft(h);

l=zeros(length(s1),1);

for i=1:length(h_dft)

w(i)=h(i);

end

for i=(length(h_dft)+1):length(s1)

w(i)=0;

end;

h_dft=fft(w);

for i=1:length(s1)

l(i)=s1(i)*h_dft(i);

end;

[roz_h_dft,cos]=size(h_dft);%wyznaczanie rozmiaru sygnału h_dft

czestotliwosc=0:(fs/roz_h_dft):(fs*(roz_h_dft-1)/roz_h_dft);

figure(10)

stem(czestotliwosc,abs(l));

title('Widmo amplitudowe filtru pasmoprzepustowego (za pomoca dft)');

figure(11);

plot(czestotliwosc,abs(h_dft));

title('Charakterystyka amplitudowa filtru pasmoprzepustowego (za pomoca dft)')

rys. 12 Widmo amplitudowe filtru pasmo przepustowego (z DFT)

rys. 13 Charakterystyka amplitudowa filtru pasmo przepustowego (z DFT)

• wykorzystując funkcję conv;

W tym przypadku wystarczyło użyć wbudowanej funkcji środowiska MATLAB i wyświetlić odpowiednie wykresy, realizuje to skrypt:

y=conv(s,h);

[n,x]=size(y);

czestotliwosc=0:(fs/n):(fs*(n-1)/n);

figure(12)

A=fft(y);

stem(czestotliwosc,abs(A));

title('Widmo amplitudowe filtru pasmoprzepustowego (conv)');

figure(13);

czestotliwosc=0:(fs/N):(fs*(N-1)/N);

plot(czestotliwosc,abs(fft(h)));

title('Charakterystyka amplitudowa filtru pasmoprzepustowego (conv)')

wavwrite(y,fs,'dzwiek_po_filtracji_pasmo');

rys. 14 Widmo amplitudowe filtru pasmo przepustowego (conv)

rys. 15 Charakterystyka amplitudowa filtru pasmo przepustowego (conv)

9.8

Należało zbadać wpływ rzędu na jakoś filtru, aby to wykonać zamieniałem wartości N z zadania 9.6 i kolejno wyświetlałem wykresy dla różnych wartości.

rys. 16 N=101

rys. 17 N=301

rys. 18 N=501

Jakość tych wykresów także określamy za pomocą stromizny jaka na nim występuje. Im ona jest większa, tym wykres jest lepszej jakości. Od razu widać, że jakość tych wykresów się poprawia. Ze zwiększaniem rzędu N wykres był coraz bardziej stromy i występował coraz bliżej naszych kluczowych wartości fc1=1000Hz, fc2=2000Hz.

Wnioski

Filtr pasmo przepustowy jest różnicą dwóch filtrów dolnoprzepustowych. Widmo amplitudowe sygnału po filtracji funkcją conv posiada więcej składowych harmonicznych niż ten po filtracji za pomocą DFT. Widma amplitudowe dzięki wykorzystaniu DFT sygnału badanego i przefiltrowanego mają tę samą długość. Filtr dolnoprzepustowy zeruje wartości większe od częstotliwości granicznej a filtr pasmo przepustowy zeruje wszystkie nie należące do zadanego pasma. Odsłuchując dźwięk po filtracji dolnoprzepustowej można stwierdzić, że jest on niższy, przytłumiony i trochę cichszy, jednak jakoś nie odbiega dużo od oryginału. Z kolei po filtracji pasmo przepustowej dźwięk jest dużo gorszej jakości, ledwo słyszalny, jednak jesteśmy w stanie rozróżnić co jest wypowiadane.

---