Kinematyka punktu
Ruch - jest to zjawisko zmiany położenia ciała względem innego ciała uznanego umownie za nieruchome.
Nieruchome ciało nazywamy ciałem odniesienia.
Czas - jest w mechanice klasycznej (Newtona) pojęciem pierwotnym i absolutnym.
-Czas nie zależy od wyboru układu odniesienia i jest taki sam w każdym punkcie przestrzeni.
-Przyjmuje się, że czas jest stale nieujemny t Ⴓ 0
i występuje tylko wtedy gdy występuje ruch.
Układ odniesienia - jest to układ współrzędnych sztywno związany z ciałem odniesienia, który służy do opisu ruchu obiektu (-ów).
Tor ruchu punktu - równanie krzywej, po której następuje ruch tego punktu, np.:
y = y(x) y = 3x2 - 6x + 5
1) KINEMATYKA PUNKTU W UKL. Ozyz
Opis ruchu punktu
Matematycznie ruch punktu opisujemy w postaci wektorowej lub skalarnej. Opisy te są równoważne
Równanie wektorowe ruchu: r = r(t)
Równania skalarne w ukł. Oxyz: x=x(t), y=y(t), z=z(t)
Prędkość punktu w Oxyz
![]()
Wektor prędkości:
![]()
przy czym ![]()
Wartość prędkości (długość wektora):
![]()
Elementarna droga po torze:
![]()
Jeśli znamy s=s(t) to prędkość możemy obliczyć z zależności:
![]()
Przyspieszenie punktu w Oxyz
![]()
Wektor przyspieszenia punktu ma na ogół
inny kierunek niż wektor prędkości !
Wektor przyspieszenia i jego współrzędne:
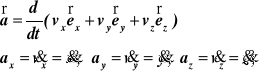
Moduł przyspieszenia (długość wektora przyspieszenia):
![]()
2) KINEMATYKA PUNKTU W UKŁ. NATURALNYM
Założenia:
- Ruch punktu jest dany w postaci:
![]()
Początek układu współrzędnych jest związany
z ruchomym punktem A na torze. Układ taki nazywamy naturalnym lub trójścianem Freneta (rys nizej)
A t n b - układ naturalny
t, n, b - zależą od czasu.
t - wersor ściśle styczny,
n - wersor normalny główny,
b - wersor binormalny b=tႴn
Wektory t i n wyznaczają płaszczyznę
ściśle styczną do toru -p.
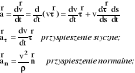
Przyspieszenie punktu w układzie naturalnym
ၲ - promień krzywizny toru w punkcie A
Kinematyka ciała sztywnego (CS)
1)RUCH CS SWOBODNEGO
Ciało sztywne - zbiór punktów, między którymi wzajemne odległości są stałe.
Ruch CS w przestrzeni E3 jest jednoznacznie opisany
za pomocą trzech punktów sztywno związanych z tym ciałem
i nie leżących na jednej prostej.
Dla trzech punktów: A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC)
mamy równania wektorowe ruchu:
![]()
Liczba stopni swobody c.s.
Zauważmy, że dla CS odległości między p-tami A, B, C są stałe:
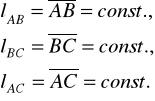
Liczba stopni swobody CS - liczba niezależnych współrzędnych określających położenie tego ciała.
W przestrzeni E3 CS w ruchu dowolnym posiada:
k=9-3=6 stopni swobody.
Po nałożeniu na ciało sztywne pewnych ograniczeń
ruchu (więzów), zmniejszamy liczbę stopni swobody;
np. w ruchu obrotowym wokół stałej osi CS ma 1 stopień swobody (kąt obrotu wokół tej osi).
Prędkości dwóch dowolnych p-tów CS
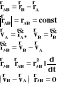
![]()
Twierdzenie o prędkościach dwóch dowolnych p-tów CS
Rzuty wektorów prędkości dwóch dowolnych p-tów CS na
prostą łączącą te punkty są sobie równe.
![]()
Klasyfikacja ruchów ciała sztywnego
Ogólnym przypadkiem ruchu CS jest ruch dowolny (swobodny) względem nieruchomego układu Oxyz
Ruch dowolny CS; k=6
Ruch postępowy CS; k=3
Ruch obrotowy CS wokół stałej osi; k=1
Ruch płaski CS; k=3
Ruch kulisty CS; k=3
2) RUCH DOWOLNY CS
Do opisu tego ruchu wprowadzimy dwa układy odniesienia:
Oxyz - układ stały (nieruchomy),
O1x1y1z1 - układ ruchomy względem Oxyz.
Interpretacja geometryczna ruchu dowolnego:
Ruch p-tu AC1 მ ruch bieguna 01 +
+ ruch wokół bieguna 01
Przyspieszenie dowolnego punktu A
![]()
![]()
- wektor wodzący punktu A w układzie Oxyz.
![]()
- wektor wodzący punktu A w układzie O1z1y1z1
![]()
- wektor wodzący bieguna O1 w układzie Oxyz.
Chwilowy ruch obrotowy ciała C1 (Ruch wokół bieguna 01)
Wektor chwilowej prędkości kątowej ciała C1
![]()
![]()
- jest wektorem zmieniającym swój
kierunek lecz zawsze leżącym na chwilowej osi obrotu.
Prędkość p-tu A ciała w jego chwilowym
ruchu obrotowym
Torem punktu A jest łuk okręgu o promieniu h.
h=rთsina
![]()
![]()
![]()
- wektor prędkości punktu A ciała sztywnego
w chwilowym ruchu obrotowym
Prędkość dowolnego punktu A
![]()
![]()
![]()
![]()
Przyspieszenie dowolnego punktu A
Przyspieszenie punktu A CS względem Oxyz: ![]()
![]()
Podstawiamy:
![]()
![]()
- wektor przyspieszenia kątowego, [rad/s2]
![]()
Gdzie:
![]()
- przysp. bieguna O1 (początku układu O1x1y1z1)
względem Oxyz,
![]()
- przyspieszenie obrotowe,
![]()
- przyspieszenie doosiowe (dośrodkowe)
3) RUCH POSTEPOWY CS
Występuje wtedy, kiedy prosta łącząca dwa dowolne p-ty tego ciała przemieszcza się równolegle względem swego położenia początkowego w czasie ruchu.
AB||A1B1 r=const
Po zróżniczkowaniu:
W ruchu postępowym wszystkie punkty ciała sztywnego mają takie same wektory prędkości i przyspieszenia i poruszają się po torach przystających.
Wnioski:
*Ruch postępowy CS jest określony jeżeli znamy ruch dowolnego punktu tego ciała.
Równania ruchu dowolnego punktu A ciała:
xA=xA(t), yA=yA(t), zA=zA(t)
*CS w ruchu postępowym ma 3 stopnie swobody.
4) RYCH OBROTOWY CS WZGL. STAŁEJ OSI
Występuje wtedy kiedy jedna prosta związana z tym ciałem jest nieruchoma.
![]()
Każdy punkt ciała sztywnego w ruchu obrotowym porusza się po okręgu, którego płaszczyzna jest prostopadła do osi obrotu
Predkość i przyspieszenie kątowe w ruchu obrotowym
Wektor prędkości kątowej:
![]()
Wektor przyspieszenia kątowego:
![]()
![]()
Wartości prędkości i przyspieszenia:
![]()
Prędkość i przyspieszenie dowolnego punktu A
Wektor prędkości dowolnego punktu A
![]()
Wartość (moduł) wektora prędkości dowolnego punktu A:
![]()
Wektor przyspieszenia dowolnego punktu A
![]()
Wprowadzamy oznaczenia:
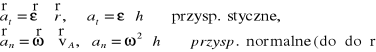
Wartość (moduł) wektora przyspieszenia punktu A:
![]()
Przyspieszenie styczne i dośrodkowe dowolnego punktu A
![]()
Wniosek:
a - nie zależy od wyboru punktu A
Ruch obrotowy jednostajny i jednostajnie zmienny CS
1. Ruch obrotowy jednostajny: w = const,
Równanie ruchu jednostajnego: ၪ(t) = w t + ၪ0
2. Ruch obrotowy jednostajnie zmienny: e = const,
Równania ruchu jednostajnie zmiennego:
ၷ(t) = ၥ t + ၷ0 , ၪ(t) = 0.5 e t2 + w0 t + ၪ0
5) RUCH PŁASKI CS
Ruch, w którym wszystkie punkty
tego ciała poruszają się w nieruchomych płaszczyznach
równoległych do pewnej płaszczyzny ၰo - zwanej
płaszczyzną kierującą .
W ruchu płaskim wszystkie punkty CS leżące na prostej l
mają jednakowe prędkości i przyspieszenia oraz poruszają
się po identycznych torach.
Wniosek:
Ruch płaski CS można zastąpić ruchem figury płaskiej F,
pozostającej w czasie ruchu na płaszczyźnie ၰ.
Do opisu położenia tej figury wystarczy wybrać dwa dowolne
punkty A(xA,yA) i B(xB,yB) a więc 4 współrzędne kartezjańskie.
Liczba stopni swobody CS w ruchu płaskim.
Odległość między p-tami A i B jest dla CS stała, czyli
równanie więzów (wzór na odległość między A i B) ma
postać:
d2 =(xA2 - xB2) + (yA2 - yB2) = const.
Liczba stopni swobody: k = 3;
k = 2n - a = 2 თ 2 - 1 = 3;
n =2 Ⴎ liczba punktów (A i B),
a =1 Ⴎ liczba równań więzów;
Równania ruchu płaskiego
Skoro ruch figury F jest opisany za pomocą dwóch dowolnych
punktów A i B sztywno z nią związanych, to ruch tej figury
zastąpimy odcinkiem AB.
Równania ruchu (k = 3):
xA = xA(t), yA = yA(t), ၪ = ၪ(t);
Prędkość i przyspieszenie kątowe w ruchu płaskim.
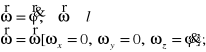
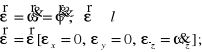
Prędkość dowolnego punktu A
Korzystamy ze wzoru wektorowego na prędkość dowolnego
p-tu CS w ruchu dowolnym
![]()

![]()
![]()
ၞ![]()
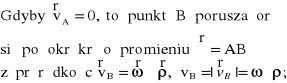
Chwilowy środek obrotu figury płaskiej
To taki punkt C sztywno związany z figurą płaską F, którego prędkość w danej chwili czasu jest równa zeru.
*Wokół chwil. środka obrotu C ruch trwa nieskończenie krótko.
*Wraz z ruchem CS (figury F ) zmienia się położenie p-tu C. *Jeśli chwilowy środek obrotu C istnieje, to jego prędkość
w danej chwili czasu jest równa zeru: vC = 0 !
chwilowy środek obrotu მ chwilowy środek prędkości
Wyznaczanie chwilowego środka obrotu![]()
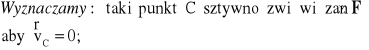
1) prowadzimy prostą p ၞ ![]()
![]()
2) obieramy Cp tak aby
![]()
![]()
Stąd otrzymujemy:![]()
Odległość chwilowego środka obrotu Cp od bieguna A:
![]()
Zastosowania
Przyspieszenie punktu CS w ruchu płaskim
Korzystamy ze wzoru na przysp. punktu CS w ruchu dowolnym![]()

Wzór na przyspieszenie dowolnego p-tu B figury F ma postać:
![]()
Oznaczenia wektorów składowych:

Wartości przyspieszeń składowych:
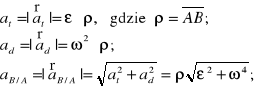
![]()
DYNAMIKA
RÓWNANIA RUCHU PUNKTU MATERIALNEGO
1)PRAWA DYNAMIKI NEWTONA
I prawo (bezwładności):
Istnieje układ odniesienia, w którym punkt materialny porusza się bez przyspieszenia (tzn. jednostajnie i prostoliniowo) gdy z zewnątrz nic na niego nie działa.
Wniosek: Siła jest jedyną przyczyną zmiany ruchu punktu materialnego.
Układ inercjalny - układ odniesienia, w którym można
stwierdzić I prawo dynamiki.
Jeżeli oraz są w czasie ruchu stale równe zeru to układ 0xiyizi jest układem inercjalnym.
II prawo (podstawowe):
W inercjalnym układzie współrzędnych wektor siły
działającej na punkt materialny jest proporcjonalny
do wektora przyspieszenia.
![]()
m-masa bezwładna (jest równoważna masie grawitacyjnej)
Bezwładność - właściwość obiektu polegająca na przeciwstawianiu się zmianom ruchu tego obiektu.
Dynamiczne równania ruchu w postaci skalarnej mają postać: *W układzie inercjalnym Oxyz:
![]()
W układzie naturalnym (Freneta):
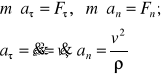
III prawo (akcji i reakcji):
Siły wzajemnego oddziaływania dwóch punktów
materialnych są równe co do wartości, mają przeciwne zwroty i wspólną linię działania.![]()
III prawo jest słuszne w układach inercjalnych i nieinercjal- nych ponieważ nie zawiera ono pojęć kinematycznych takich jak prędkość lub przyspieszenie.
Zgodnie z III prawem Newtona warunkiem powstania siły jest występowanie co najmniej dwóch ciał.
2) ZADANIE PROSTE I ODWROTNE DYNAMIKI
Zadanie proste:
Dane są równania ruchu np.: x=x(t), y=y(t), z=z(t)
(tzn. lewe strony dynamicznych równań ruchu)
Wyznaczamy współrzędne siły: Fx, Fy, Fz
(tzn. prawe strony dynamicznych równań ruchu)
Zadanie odwrotne:
Dane są siły (współrzędne siły): Fx, Fy, Fz
(tzn. prawe strony dynamicznych równań ruchu);
oraz warunki początkowe ruchu (dla t=0).
Wyznaczamy równania ruchu: x=x(t), y=y(t), z=z(t)
(tzn. lewe strony dynamicznych równań ruchu).
3)RÓWNANIA RUCHU PUNKTU MAT. W UKŁ. NIEINERCJALNYM
Wprowadzamy:
stały układ odniesienia Oxyz,
nieinercjalny układ odniesienia O1x1y1z1,
dla którego w Ⴙ 0 i a01 Ⴙ 0;
Na punkt A o masie m działa siła F.
Równanie ruchu p-tu A w układzie stałym (inercjalnym):
![]()
![]()
![]()
Wektorowe równanie ruchu p-tu A w układzie
nieinercjalnym 01x1y1z1:
![]()
lub![]()
Wprowadzono oznaczenia:
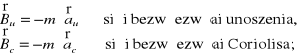
![]()
- nazywamy siłami fikcyjnymi (pozornymi),
ponieważ nie są one wynikiem oddziaływań
z innymi obiektami w takim znaczeniu jak siły F.
4)SIŁA BEZWŁADNOŚCI I ZASADA D'Alamberta
Siła bezwładności
Z II prawa dynamiki Newtona:![]()
Jeżeli wektor -m·a potraktujemy jako pomyślaną siłę, to równanie powyżej możemy rozpatrywać jako warunek równowagi siły F działającej na punkt materialny i siły -m·a
B = -m·a - siła bezwładności (tzw. siła fikcyjna);
II prawo dynamiki można przedstawić jako równanie
równowagi wypadkowej sił rzeczywistych F i siły
bezwładności B w czasie ruchu punktu. ![]()
F - wypadkowa sił rzeczywistych (akcji i reakcji),
B - siła bezwładności;
Zasada d'Alamberta
Jeżeli w inercjalnym układzie współrzędnych do wszystkich sił rzeczywistych F1, F2,..., Fn dołączymy
siły bezwładności B1, B2,..., Bn to otrzymany układ sił
spełnia formalnie statyczne warunki równowagi.
lub
Wypadkowa sił rzeczywistych działających na punkt materialny równoważy się w każdej chwili z siłą bezwładności tego punktu.
ZASADY ZMIENNOŚCI W DYNAMICE PUNKTU MATERIALNEGO
1)Pęd punktu materialnego(ilość ruchu PM)
![]()
![]()
Moduł wektora pędu: ![]()
Jednostka pędu:
![]()
Związek wektora pędu PM z siłą działającą
na ten punkt i z II prawem dynamiki Newtona
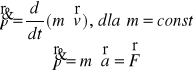
![]()
Różniczkowa zasada zmiany wektora pędu:
Pochodna po czasie wektora pędu PM jest równa wektorowi siły działającej na ten punkt.
Różniczkową zasadę zmiany pędu możemy również przedstawić:
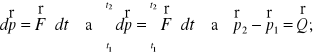
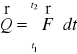
-impuls siły lub popęd (t1ြt2)
![]()
Całkowa zasada zmiany pędu:
Zmiana wektora pędu w skończonym przedziale czasu (t2-t1)
jest równa impulsowi wektora siły w tym przedziale.
W szczególności, jeśli F = 0:![]()
Zasada zachowania pędu punktu materialnego:
Jeżeli wypadkowy wektor sił działających na PM
jest równy zeru to wektor pędu jest stały.
Uwaga: w praktyce może mieć miejsce sytuacja, np.:
![]()
wówczas
![]()
2)PRACA I MOC SILY, ENERGIA KIN. PM
![]()
![]()
![]()
![]()
![]()
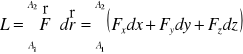
1[N]თ1[m]=1[J]
Moc siły
![]()
Pracę wykonaną przez siłę w ciągu jednostki
czasu nazywamy mocą tej siły.Moc oznaczamy przez N
![]()
Energia kinetyczna i zasada równoważności pracy
i energii kinetycznej
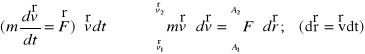
![]()
Energia kinetyczna p.m.: ![]()
Zasada równoważności:
Zmiana energii kinetycznej PM w skończonym przedziale czasu jest równa sumie prac, które wykonały w tym samym czasie wszystkie siły działające na ten punkt.
Zasada zachowania energii mechanicznej PM
Zasada zachowania jest szczególnym przypadkiem zasady
równoważności pracy i energii kinetycznej PM
*Załóżmy, że w pewnym obszarze przestrzeni ၗ działa pole sił: ![]()
*Jeśli w każdym punkcie przestrzeni ၗ to takie pole nazywamy jednorodnym. ![]()
*Jeśli: ![]()
to takie pole nazywamy potencjalnym.
V=V(x,y,z) - jest potencjałem pola sił lub energią potencjalną PM
*Wtedy pracę L w potencjalnym polu sił przedstawimy:
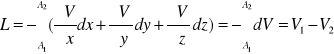
Wniosek:
Praca w potencjalnym polu sił nie zależy od drogi lecz tylko od położenia początkowego i końcowego.
Zasada zachowania energii mechanicznej PM:
Po podstawieniu powyższego wzoru na pracę L do prawej strony wzoru wyrażającego zasadę równoważności pracy i energii kinetycznej otrzymamy: ![]()
Em = E + V -nazywamy energią mechaniczną
3)KRĘT(MOMENT PĘDU) PM
![]()
; ![]()
Zasada zmiany krętu p.m.: ![]()
Zasada zachowania krętu p.m.: Jeśli M = 0 dla tႳ0 to mamy
![]()
4)PODSTAWY TEORII MOMENTÓWBEZWŁADNOŚCI
Środek masy i środek ciężkości UPM i CS
Założenia:
*Weźmy pod uwagę układ n punktów materialnych o
masach mi (i=1,...,n)
*Położenie tych punktów w stosunku do punktu
odniesienia O określone jest wektorami ri
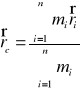
; ![]()
Punkt C nazywamy środkiem masy UPM.
Środek masy UPM w układzie Oxyz
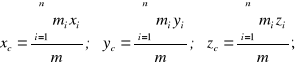
![]()
Pojęcie środka masy ma charakter ogólny i może być zastosowane do dowolnego UPM, niezależnie od tego czy układ jest sztywny czy nie, czy jest w ruchu czy w spoczynku oraz czy znajduje się w polu sił.
Środek masy ciała sztywnego ciągłego
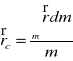
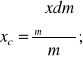
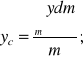
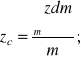
Gęstość CS ciągłego
Gęstość CS dowolnego: ![]()
Gęstość CS jednorodnego: ![]()
Gęstość CS dwuwymiarowego: ![]()
(powłoki, cienkie płyty)
Gęstość CS jednowymiarowego: ![]()
(pręty, liny, belki)
Środek ciężkości
Na obiekty znajdujące się w polu przyciągania Ziemi, działają siły ciążenia. Siły te zastępujemy wypadkową siłą ciężkości. Przy założeniu, że rozmiary obiektu są małe w porównaniu do rozmiarów Ziemi można siły ciężkości uznać za równoległe i wyznaczyć środek równoległych sił ciężkości. Punkt taki nazywamy środkiem ciężkości obiektu (UPM lub CS).
Środek ciężkości UPM:
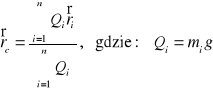
Ciężar właściwy CS: ![]()
Środek masy CS jednorodnego
Wzory na środek masy CS upraszczają się gdy mamy do czynienia z ciałem jednorodnym tzn. takim, w którym masa jest rozłożona równomiernie w całej jego objętości.
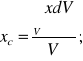
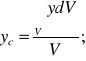
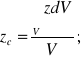
Podsumowanie
*Ze wzorów na środek masy wynika, że jego
położenie w jednorodnym CS zależy tylko od
jego geometrii.
Ogólne własności jednorodnego CS:
* Jeżeli ciało ma płaszczyznę symetrii to środek
masy leży na tej płaszczyźnie.
*Jeżeli ciało ma oś symetrii to środek masy leży na
tej osi.
*Jeżeli ciało ma środek symetrii to środek masy
leży w tym środku.
5)MOMENTY STATYCZNE
Momentem statycznym UPM względem płaszczyzny nazywamy sumę iloczynów mas każdego punktu przez ich odległości od tej płaszczyzny.
Np. względem płaszczyzny 0xy:
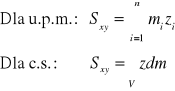
Momenty statyczne a środek masy
Współrzędne środka masy można określić za pomocą momentów statycznych względem płaszczyzn układu Oxyz:
![]()
![]()
![]()
6)MOMENTY BEZWŁADNOŚCI
Momenty bezwładności względem płaszczyzn Oxyz
Dla UPM:
![]()
Dla CS:
![]()
Momenty bezwładności względem osi 0xyz
Dla UPM: ![]()
Dla CS:
![]()
Moment bezwładności względem bieguna 0
Dla UPM: ![]()
Dla CS: ![]()
Ważne zależności
![]()
![]()
![]()
Momenty dewiacyjne (mieszane) w układzie Oxyz
Dla UPM: ![]()
Dla CS:![]()
![]()
;![]()
Macierz bezwładności (tensor bezwładności)
I = 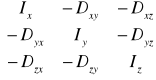
I - opisuje własności bezwładnościowe CS lub UPM
Moment bezwładności względem dowolnej osi l
l - dowolna prosta przechodząca przez początek układu 0
![]()
Po przekształceniach moment bezwładności względem osi l wynosi:
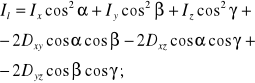
Osie główne centralne i momenty bezwładności
względem nich
Lokując początek układu współrzędnych w środku masy ciała mamy centralny układ osi Cxyz.
Jeżeli tak zorientujemy w przestrzeni osie układu Cxyz, że
Dxy=Dxz=Dyz=0, to takie osie nazywamy głównymi centralnymi.
Układ takich osi oznaczamy: C123.
Momenty bezwładności względem osi głównych centralnych
oznaczamy odpowiednio: I1, I2, I3 i nazywamy
głównymi centralnymi momentami bezwładności c.s.
Moment bezwładności względem dowolnej osi l, wyrażony
w układzie głównym centralnym C123 ma postać:
![]()
Momenty bezwładności względem osi równoległych
Twierdzenie Steinera
Moment bezwładności CS względem dowolnej osi l1 jest równy sumie momentu bezwładności względem osi do niej równoległej l przechodzącej przez środek masy tego ciała oraz iloczynu masy ciała i kwadratu odległości między tymi osiami.
![]()
ZASADY ZMIENNOŚCI W DYNAMICE UPM i CS
1)Pęd układu punktów materialnych(pęd główny)
![]()
To jest sumowanie wektorów a więc sumowanie geometryczne
Zasada zmiany pędu głównego:
![]()
Suma wektorów sił wewnętrznych:
![]()
Zgodnie z III prawem dynamiki Newtona:
![]()
![]()
Fz - wektor główny sił zewnętrznych (wektor wypadkowy)
Różniczkowa zasada zmiany pędu głównego:
Pochodna po czasie wektora pędu głównego jest równa wektorowi głównemu sił zewnętrznych działających na UPM.
Podobnie jak dla pojedynczego punktu, można wyprowadzić
całkową zasadę pędu głównego.
Zasada ruchu środka masy UPM
Z równości momentu statycznego środka masy UPM i sumy
momentów statycznych wszystkich punktów tego układu:
![]()
![]()
M - całkowita masa u.p.m.
![]()
- wektor przyspieszenia środka masy UPM
Środek masy u.p.m. porusza się tak jak punkt o masie M pod
wpływem wszystkich sił zewnętrznych działających na ten układ.
2) Praca i energia kinetyczna UPM
C - środek masy u.p.m
![]()
;
![]()
![]()
Po przekształceniach otrzymujemy (twierdzenie Königa):
![]()
![]()
- energia kinetyczna środka masy u.p.m
Ew - energia kinetyczna u.p.m. w jego ruchu względem środka masy C
Twierdzenie Königa:
Energia kinetyczna u.p.m. jest równa sumie energii kinetycznej
jaką miałby p.m. o masie całego układu, poruszający się z prędkością środka masy, oraz energii kinetycznej tegoż układu w jego ruchu względem środka masy.
3)Kręt główny (kręt UPM)
![]()
![]()
Zasada zmiany krętu głównego:
![]()
Z ostatniego równania wynikają następujące równania
na współrzędne wektora krętu w układzie Oxyz:
![]()
Mx, My, Mz - momenty sił zewnętrznych względem
odpowiednich osi współrzędnych
Jeśli na układ nie działają żadne siły zewnętrzne to
Mx =My= Mz =0. Wówczas ma miejsce zasada zachowania
krętu:![]()
4)Pęd ciała sztywnego
![]()
m - masa ciała sztywnego,
Vc - prędkość środka masy c.s.
Zasada zmiany pędu CS
![]()
![]()
![]()
- wektor wypadkowy sił zewnętrznych
działających na środek masy c.s.
Zasada zmiany pędu c.s.:
Pochodna względem czasu wektora pędu c.s. jest równa
wektorowi wypadkowemu sił zewnętrznych działającemu
na środek masy tego ciała.
5)Energia kinetyczna CS i praca
![]()
Energia kinetyczna CS w ruchu dowolnym
![]()

Il=const w ruchu obrotowym wokół stałej osi obrotu.
Energia kinetyczna CS w ruchu postępowym
![]()
Energia kinetyczna CS w ruchu obrotowym wokół stałej osi:
![]()
Energia kinetyczna CS w ruchu płaskim:
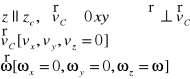
![]()
6)Kręt (moment pędu) ciała sztywnego
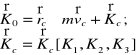
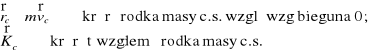
Współrzędne wektora krętu w układzie C123:
K1 =I1ၷ1 ; K2 =I2 ၷ2 ; K3 =I3 ၷ3
Zasada zmiany wektora krętu CS
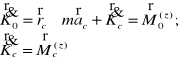
Kręt CS w ruchu obrotowym wokół stałej osi
Jeśli prosta z jest osią obrotu CS to jego kręt (współrzędna)
wynosi:
![]()
![]()
Zasada zmiany kretu
![]()
Jeśli Mz = 0 to otrzymujemy zasadę zachowania krętu CS:
![]()
6) Dynamiczne równania ruchu CS
Dynamiczne równania CS w ruchu dowolnym
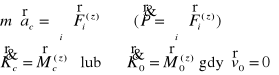
![]()
- suma sił czynnych i reakcji działających na CS.
Dynamiczne równania CS w ruchu postępowym
![]()
Wniosek
Ruch postępowy ciała sztywnego jest równoważny
ruchowi punktu.
Ciało sztywne swobodne w ruchu postępowym ma k=3 stopnie swobody (tak jak punkt).
Dynamiczne równania ruchu obrotowego wokół stałej osi.
l - dowolna stała oś obrotu c.s
C.s. w ruchu obrotowym wokół stałej osi ma k=1 st. swobody
Z zasady zmiany krętu CS dla ruchu obrotowego wokół stałej
osi otrzymamy:
![]()
![]()
Stąd dynamiczne równanie ruchu obrotowego wokół dowolnej
stałej osi l :
![]()
Powyższe równanie nie zależy od sił reakcji w łożyskach lecz tylko od sił czynnych zewnętrznych.
Dwa przypadki wyrównoważenia
1. Wyrównoważenie dynamiczne: RA=RB=0, czyli kiedy oś
obrotu jest jedną z głównych centralnych osi bezwładności,
nazywamy ją wówczas osią swobodną.
2. Wyrównoważenie statyczne: xc=yc=0 ale Dxz Ⴙ 0 i Dyz Ⴙ 0,
oś obrotu jest wtedy osią centralną lecz nie główną.
Reakcje dynamiczne natomiast tworzą parę sił :
![]()
Wzory pomocnicze przy obliczaniu reakcji dynamicznych
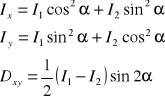
Wyszukiwarka