Wyższa Szkoła Technologii informatycznych

Elektronika dla informatyków - laboratorium

Ćwiczenie nr 1 - badanie obwodów prądu stałego

Data wykonania ćwiczenia: 27.02.07 r.

Wykonujący: Paulina Wojda - ID-2/II

Dawid Chojnowski - ID-2/II

1 Cel Ćwiczenia

Celem ćwiczenia jest doświadczalne sprawdzenie praw obowiązujących w obwodach prądu stałego, sprawdzenie zasadności stosowania niektórych twierdzeń i metod obliczeniowych oraz obserwacja wpływu rezystancji wewnętrznej mierników i konfiguracji układu pomiarowego na błędy pomiarów prądów i napięć. Ćwiczenie składało się z trzech niezależnych części.

2 Pomiary dużych i małych prądów

2.1 Procedura pomiarowa

Schematy układów badanych przedstawiaj¡ poniższe rysunki:

Po przyjściu wartości rezystancji R_o = 50
podano napięcie zasilające U_zas = 2,98V, a następnie odczytano wartości prądu i napięcia wskazywane przez mierniki - dla układu 1 oraz dla układu 2. Następnie zmieniono wartości rezystancji na R_o = 1M
, podano napięcie zasilające U_zas = 31,41V i ponownie zmierzono wartości prądu i napięcia wskazywane przez mierniki. Wyniki pomiarów przedstawia tabela:

	R0 = 50		R0 = 1M
Układ	1	2	3	4
U	2,980V	2,970V	31,41V	31,42V
I	59,8mA	62,1mA	031,7 A	034,8 A

2.2 Wnioski z pomiarów

Z przeprowadzonych pomiarów widać, że zmiana układu pomiarowego spowodowała zmianę wartości prądów i napięć odczytanych z amperomierza i woltomierza. Przyczyny tego zjawiska jest rezystancja wewnętrzna mierników. W przypadku włączanego w szereg amperomierza powinna być ona jak najmniejsza (w idealnym przypadku - zerowa), natomiast w przypadku włączanego równolegle woltomierza powinna być jak największa (w idealnym przypadku - nieskończenie duża). W rzeczywistości rezystancja wewnętrzna amperomierza R_weA wynosi kilka omów, zaś rezystancja wewnętrzna woltomierza R_weV jest rzędu megaomów.

W układzie 1 woltomierz mierzy sumę spadków napięć na rezystancji obciążenia R_o oraz na rezystancji R_weA . Jeżeli wartości rezystancji R_o jest zbliżona do wartości R_weA, to pomiar spadku napięcia na R_o jest obarczony dużym błędem. Z kolei w układzie 2 amperomierz mierzy sumę prądów przepływających przez R_o oraz przez rezystancji R_weV . Jeżeli wartość rezystancji R_o jest zbliżona do wartości R_weV , to pomiar prądu płynącego przez R_o jest obarczony dużym błędem.

Z przeprowadzonych pomiarów wynika, że opisane układy nie powinny być stosowane zamiennie - układ 1 powinien być stosowany do pomiaru dużych rezystancji, natomiast układ 2 powinien być stosowany do pomiaru małych rezystancji.

3 Sprawdzenie metod transfiguracji obwodu

3.1 Procedura pomiarowa

Schemat badanego układu przedstawia rysunek:

Na początku pomiarów przy pomocy omomierza zmierzono wartości rezystorów w układzie. Następnie, po załączeniu napięcia zasilającego wykonano pomiary napięć i prądów mierzonych przez mierniki. Wyniki wszystkich pomiarów zapisano w poniższej tabeli:

Pomiary									Obliczenia
U[V]	IA[mA]	IE,F[mA]	RA[ ]	RB[ ]	RC[ ]	RD[ ]	RE[ ]	RF[ ]	Robl[ ]	Rteor[ ]	IE,F[mA]
19,79	24,03	08,91	047,6	2,01 · 10^3	09,92	0,500	0,978	0,984	0,500	0,978	0,984

3.2 Opracowanie wyników

3.2.1 Wyznaczenie rezystancji zastępczej układu R_obl metodą techniczną

W metodzie technicznej wartość nieznanej rezystancji R_x wyznaczamy poprzez jednoczesny pomiar prądu I_x płynącego przez tą rezystancją i napięcia U_x panującego na tej rezystancji; nieznana rezystancja - na mocy prawa Ohma - jest więc równa

R_{x =}

W naszym przypadku R_obl wyliczamy jako

R_{obl =}

Po podstawieniu U = 19,79V, I_A = 24,03mA otrzymujemy R_obl = 0,824
.

2. Obliczenie teoretycznej rezystancji zastępczej Rteor metodą

transfiguracji układu

Metoda transfiguracji (przekształcania) obwodu polega na wykorzystaniu zależności dotyczących połączenia szeregowego i równoległego elementów oraz przekształceń połączenia elementów w gwiazdę na połączenie w trójkąt i odwrotnie. Dzięki tym przekształceniom układ stopniowo się upraszcza. Przekształceń dokonujemy dopóty, dopóki cały układ nie zostanie zastąpiony jednym elementem zastępczym.

Po zastąpieniu amperomierzy zwarciami a woltomierzy rozwarciami układ ma postać jak na rysunku:

Zaznaczone linią przerywaną połączenie rezystorów R_B, R_F, R_D jest połączeniem w trójkąt. Połączenie to zamieniamy na gwiazdą złożoną z rezystorów R_BD, R_BF, R_DF:

Wartości tych rezystorów są równe:

R_BD =
0,5

R_BF =
0,99

R_DF =
0,00024

Jak widać na ostatnim rysunku, mamy trzy układy połączeń szeregowych, które można uprościć:

- połączone szeregowo rezystory R_BF i R_C zastępujemy rezystancją RBFC równą

R_BFC = R_BF + R_C = 10,91

- połączone szeregowo rezystory R_DF i R_E zastępujemy rezystancją RDFE równą

R_DFE = R_DF + R_E = 0,98

- połączone szeregowo rezystory R_A i R_BD zastępujemy rezystancją RABD równą

R_ABD = R_A + R_BD = 48,1

Po tych zmianach układ redukuje się do postaci następującej:

Ostatecznie rezystancja zastępcza obwodu R_teor będzie równa sumie rezystancji R_ABD oraz rezystancji zastępczej połączenia równoległego R_BFC i R_DFE, co wyraża się wzorem

R_teor = R_ABD+
48,1 + 0,9 = 49

3.2.3 Obliczenie rozpływu prądu w obwodzie metodami analizy obwodów

Dla obliczenia rozpływu prądu w obwodzie przyjęto metodą prądów oczkowych. Metoda ta polega na wyznaczeniu wartości prądów oczkowych, tzn. umyślonego prądu płynącego przez wszystkie głazie danego oczka. Z prądów oczkowych wyznacza się wartości prądów gałęziowych, czyli prądów płynących przez poszczególne głazie obwodu.

W celu wyznaczenia wartości rozpływu prądów metod¡ prądów oczkowych wykonuje się następujące czynności:

1. dla danego obwodu wybieramy b - v + 1 oczek, gdzie b - liczba gałęzi, v - liczba węzłów

2. ustalamy zwroty obiegowe oczek oraz - zgodnie z nimi - ustalamy zwroty prądów oczkowych; zwroty obiegowe oczek muszą być takie same we wszystkich oczkach, np. zgodne z ruchem wskazówek zegara

3. w gałęziach ustalamy zwroty prądów gałęziowych

4. wyznaczamy rezystancje własne oczek (rezystancja własna oczka jest równa sumie rezystancji wszystkich gałęzi tworzących oczko)

5. wyznaczamy rezystancje wzajemne oczek (rezystancja wzajemna oczka 1 z oczkiem 2 jest równa rezystancji gałęzi wspólnej obu oczek; jeżeli zwroty obiegowe tych oczek są zgodne, to rezystancję wzajemną przyjmujemy jako dodatnią, jeżeli przeciwne - jako ujemną; jeżeli oczka się nie stykają, to rezystancja wzajemna jest równa zeru)

6. wyznaczamy napięcia źródłowe oczek (napięcie źródłowe oczkowe jest równe sumie napięć źródłowych wszystkich gałęzi oczka)

7. piszemy równania oczkowe zawierające związki między prądami oczkowymi a napięciami źródłowymi oczek

8. z powyższych równań obliczamy prądy oczkowe

9. z wyznaczonych prądów oczkowych wyznaczamy prądy gałęziowe przyjmując, że prąd w gałęzi wspólnej dla dwóch oczek jest równy sumie prądów oczkowych odpowiadający tym oczkom z uwzględnieniem zwrotu prądów oczkowych.

Czynności te wykonujemy dla naszego obwodu:

1. ponieważ» w obwodzie mamy 6 gałęzi i 4 węzły, więc wybieramy 3 oczka

2. ustalamy zwroty obiegowe oczek i zwroty prądów gałęziowych (zgodnie ruchem wskazówek zegara), prądy gałęziowe oznaczamy jako I₁ ; I₂ ; I₃

3. ustalamy zwroty prądów gałęziowych I_A , I_B , I_C , I_D , I_E , I_F

4. wyznaczamy rezystancje własne oczek:

R₁₁ = R_A + R_D + R_E = 49,1

R₂₂ = R_B + R_F + R_D = 2011,4

R₃₃ = R_C + R_E + R_F = 11,9

5. wyznaczamy rezystancje wzajemne oczek:

R₁₂ = R_A = -R_D = - 0,500

R₂₃ = R₃₂ = -R_F = - 0,984

R₃₃ = R₁₃ = -R_E = - 0,978

6. wyznaczamy napięcia źródłowe oczek:

E₁₁ = E = 19,79V

E₂₂ = 0

E₃₃ = 0

7. piszemy równania oczkowe:

E₁₁ = R₁₁I₁ + R₁₂I₂ + R₁₃I₃

E₂₂ = R₂₁I₁ + R₂₂I₂ + R₂₃I₃

E₃₃ = R₃₁I₁ + R₃₂I₂ + R₃₃I₃

8. w celu obliczenia niewiadomych wartości prądów I₁ , I₂ , I₃ powyższe równania

przepisujemy w postaci macierzowej:

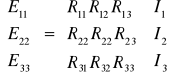
i rozwiązujemy metod¡ wyznaczników:

I₁

I₂

I₃

gdzie:

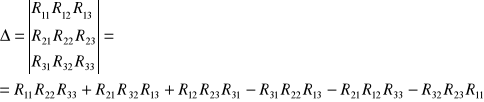
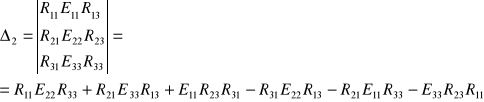
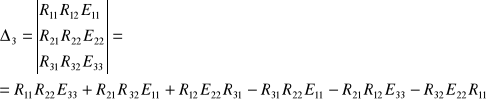
Po podstawie wartości

R₁₁ = 49,1
R₁₂ = R₂₁ = -500
E₁₁ = 19,79V

R₂₂ = 2011,4
R₂₃ = R₃₂ = -0,984
E₂₂ = 0

R₃₃ = 11,9
R₃₁ = R₁₃ = -0,978
E₃₃ = 0

otrzymujemy:

Prądy oczkowe są więc równe:

I₁
A

I₂
A

I₃
A

9. z prądów oczkowych wyznaczamy prądy gałęziowe:

I_A = I₁ = 0,00033mA

I_B = I₂ = 0,0010mA

I_C = I₃ = 0,3329mA

I_D = I₁ - I₂ = -0,00067mA

I_E = I₁ - I₃ = -0,33257mA

I_F = I₃ - I₂ = 0,3319mA

3.3 Porównanie wartości zmierzonych z wartościami uzyskami z

obliczeń

Rezystancja zastępcza obwodu Rzast
zmierzona metodą techniczną	Robl	0,824
obliczona metodą transfiguracji obwodu	Rteor	49

Wartość prądu IF płynącego przez rezystor RF
zmierzona amperomierzem	FF(A)	08,91
obliczona metodą analizy obwodów	FF(obl)	0,3319

3.4 Wnioski z pomiarów

Porównując wartości rezystancji zastępczej R_zast obwodu zmierzonej metodą techniczną i obliczonej przez przekształcenie obwodu widzimy, że obie te wartości są do siebie bardzo zbliżone. Wynika stąd wniosek, że nasze pomiary i obliczenia były prawidłowe. Została także potwierdzona prawidłowość przyjętej metody transfiguracji obwodu.

Z porównania wartości prądu I_F zmierzonego przez amperomierz i obliczonego metodą analizy obwodów również wynika, że obie te wartości są bardzo podobne. Oznacza to poprawność procedury obliczenia rozpływu prądów w obwodzie metodą prądów oczkowych.

Niewielkie różnice pomiędzy porównywanymi wartościami R_zast i I_F wynikają z błędów pomiarowych pomiaru napięć, prądów i rezystancji oraz z zaokrągleń liczb podczas wykonywania obliczeń.

• Sprawdzenie zasady superpozycji

1. Procedura pomiarowa

Schemat badanego układu przestawia rysunek:

Na początku pomiarów ustawiono wartości napięć źródłowych E₁ = 10V i E₂ = 10V,

a następnie zmierzono natężenia prądów I₁, I₂, I₃, tzn. prądów płynących przez rezystory R_A, R_B, R_E. Potem odłączono źródło napięcia E₂, zwarto po nim zaciski i zmierzono wartości prądów. Następnie ponownie podłączono źródło E₂, odłączono i zwarto zaciski po źródle E₁ oraz zmierzono wartości prądów. Wyniki pomiarów prądów przedstawia poniższa tabela:

	I1 = IA [mA]	I2 = IB [mA]	I3 = IE [mA]
Włączone źródło E1 i E2	18,30	7,46	1,18
Włączone tylko źródło E1 (IE1)	28,73	-10,43	12,61
Włączone tylko E2 (IE2)	-10,42	17,87	-11,42
Suma prądów I = EE1 + EE2	18,31	7,44	1,19

Dodatkowe zmierzono omomierzem wartości rezystancji w obwodzie:

R_A = 46,3
, R_B = 200
, R_C = 533
, R_D = 985
, R_E = 517

Wartości napięcia zasilającego obwód była równa:

E = E₁ = E₂ = 10,00V

2. Opracowanie wyników

W tym punkcie obliczymy teoretyczne wartości prądów I₁, I₂, I₃ płynących w gałęziach

R_A, R_B, R_E. Będziemy wykorzystywać zasadę superpozycji.

Przy zwartym źródle E₂ prądy płynące przez R_A, R_B, R_E wyliczamy następująco (Uwaga: G_X jest oznaczeniem przewodności rezystancji R_X):

R_DB =

R_EDB = R_E · R_DB = 683,24

R_CEDB =
299,42

R_zast = R_A · R_CEBD = 345,72

I_A(E1) =
28,92mA

I_E(E1) = I_{A(E1) ·}
12,67mA

I_B(E1) = I_E(E1)·
10,53mA

Natomiast przy zwartym źródle E₁ prądy płynące przez R_A, R_B, R_E wyliczamy następująco:

R_AC =
42,60

R_ACE = R_AC + R_E = 559,60

R_ACED =
356,86

R_zast = R_ACED · R_B = 556,86

I_B(E2) =
mA

I_E(E2) = I_{B(E1) ·}
11,44mA

I_A(E2) = I_E(E2)·
10,52mA

Prądy płynące przez R_A, R_B, R_E przy jednoczesnym działaniu źródeł E₁ i E₁ są równe - na mocy zasady superpozycji - sumie prądów płynących przez te elementy gdy działa tylko jedno źródło:

I_A = I_A(E1) + I_A(E2) = 18,4mA

I_B = I_B(E1) + I_B(E2) = 7,42mA

I_E = I_E(E1) + I_E(E2) = 1,23mA

3. Porównanie wartości zmierzonych z wartościami uzyskami z obliczeń

	I1 = IA [mA]	I2 = IB [mA]	I3 = IE [mA]
Włączone źródła E1 i E2
Z pomiarów:	18,30	7,46	1,18
Z obliczeń:	18,40	7,42	1,23
Włączone tylko źródło E1 (IE1)
Z pomiarów:	28,73	-10,43	12,61
Z obliczeń:	28,92	-10,53	12,67
Włączone tylko źródło E2 (IE2)
Z pomiarów:	-10,42	17,87	-11,42
Z obliczeń:	- 10,52	17,95	-11,44

4. Wnioski z pomiarów

Porównując wartości prądów I₁, I₂, I₃ zmierzonych przez mierniki z wartościami obliczonymi teoretycznie widzimy, ze ich wartości różnią się niewiele. Niewielkie różnice wynikają z błędów pomiaru wartości prądów, napięć i rezystancji oraz (w mniejszym stopniu) z zaokrągleń liczb podczas obliczania wyników. Nie zmienia to jednak faktu, że wyniki teoretyczne były zgodne z wartościami mierzonymi.

Porównanie wartości prądów dla przypadku działających obydwu źródeł do przypadków działających pojedynczych źródeł prowadzi do wnioski, że prądy płynące w obwodzie zasilanym dwoma źródłami są sumą prądów płynących w obwodzie zasilanym jednym źródłem przy wyeliminowaniu drugiego źródła. Oznacza to doświadczalne potwierdzenie zasady superpozycji, mówiącej że odpowiedź obwodu elektrycznego na jednoczesne działanie kilku wymuszeń jest równa sumie odpowiedzi na każde wymuszenie z osobna. Zasada ta obowiązuje tylko w obwodach liniowych. Badany obwód był obwodem liniowym.

1 Podsumowanie ćwiczenia

Podczas ćwiczenia doświadczalnie potwierdzono prawa obowiązujące w obwodach elektrycznych (prawo Ohma, prawa Kirchhoffa) oraz potwierdzono zasadność stosowania niektórych twierdzeń (zasada superpozycji) i metod obliczeniowych (metoda prądów oczkowych, transfiguracja obwodu). Zaobserwowano także wpływ rezystancji mierników na błędy pomiarów i napięć.

10

---