WYKŁAD 5. TECHNIKA INFORMACYJNO POMIAROWA

KLASYFIKACJA BŁĘDÓW

Charakter błędu:

• błąd systematyczny

• błąd przypadkowy

• błąd nadmierny (gruby)

Błędy systematyczne:

BŁĘDY SYSTEMATYCZNE to błędy, które przy wielu pomiarach tej samej wartości pewnej wielkości wykonywanych w tych samych warunkach pozostają stałe zarówno co do wartości bezwzględnej, jak i znaku lub zmieniają się wg określonego prawa wraz ze zmianą warunków otoczenia.

Błędy te modeluje się za pomocą zmiennej zdeterminowanej (przyczyna --> zdeterminowany skutek).

Błędy te można całkowicie lub częściowo wyeliminować z wyniku pomiaru za pomocą poprawek, które oblicza się teoretycznie lub wyznacza doświadczalnie.

Przyczyny występowania błędów systematycznych:

• błędy podstawowe narzędzi pomiarowych (podawane jako błędy graniczne), uproszczony model konstrukcji i niedoskonałość wykonania przyrządu, błędy wzorcowania;

• oddziaływanie przyrządu pomiarowego na wielkość mierzoną - błędy metody pomiarowej np. pobór energii ze źródła mierzonego przez przyrządy pomiarowe;

• wpływ warunków zewnętrznych (wielkości wpływających) błędy dodatkowe.

Ilustracja powstawania błędu metody:

I - wartość rzeczywista natężenia prądu stałego

I' - wartość natężenia prądu stałego wskazana przez miernik

I' < I gdy R_A > 0

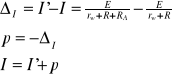
Określanie błędów systematycznych w pomiarach

a) bezpośrednich

b) pośrednich

Pomiary bezpośrednie:

- w warunkach normalnych:

X = X_m ± Δd

Δd - błąd dopuszczalny narzędzia pomiarowego

- w warunkach, które różnią się od normalnych:

X = (X_m + Σp) ± Δd

X_m + Σp - wynik pomiaru poprawiony przez usunięcie błędów dodatkowych

Gdy błędów dodatkowych nie można wyeliminować za pomocą poprawek

X = X_m ± Δx

Δx = ±[|Δd| + Σ| Δdd|]

Δd - błąd dopuszczalny narzędzia pomiarowego

Δdd - dopuszczalny błąd dodatkowy

Pomiary pośrednie:

Założenie: błędy przypadkowe są pomijalnie małe

Poszukiwana wielkość Y jest funkcją n wzajemnie niezależnych wielkości pomiarowych

X₁, X₂, …, X_n

Y = f(X₁, X₂, …, X_n)

Jeżeli X₁, X₂, …, X_n wyznaczono z błędami bezwzględnymi odpowiednio Δx₁, Δx₂, …, Δx_n i wartości tych błędów są małe to wypadkowy błąd Δy oraz błąd ςy można wyznaczyć:

- metodą przyrostów

- metodą różniczki zupełnej *

Metoda przyrostów

W praktyce metoda ta jest rzadko stosowana z uwagi na bardzo pracochłonne obliczenia

Metoda różniczki zupełnej

Załóżmy że jeżeli Y jest wyznaczane na podstawie N niezależnych wartości to wszystkie wielkości za wyjątkiem są bezbłędne

Wartość wielkości Y zamiast Y=f(X₁,X₂, …, X_n) wynosi Y+Δy = f(X₁ + Δx₁, X₂, …, X_n)

Jeżeli funkcja ta jest ciągła to można ją rozwinąć w szereg Taylora

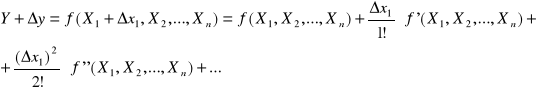
Błąd systematyczny pomiaru wielkości Y oblicza się na podstawie błędów systematycznych zgodnie z prawem liniowej propagacji błędu

- w przypadku, gdy błędy systematyczne są znane co do wartości i znaku

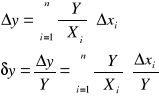
- w przypadku, gdy znane są tylko błędy graniczne pomiarów bezpośrednich (najgorszy przypadek)

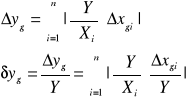
Wyznaczanie błędów granicznych dla wielkości Y prowadzi do wyników zawężonych, bowiem bardzo małe jest prawdopodobieństwo takiego zdarzenia, w którym błędy systematyczne wszystkich wielkości pomocniczych jednocześnie przyjmują wartości graniczne i niekorzystny układ znaków

Błąd średni kwadratowy

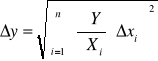
Przykład metody pośredniej

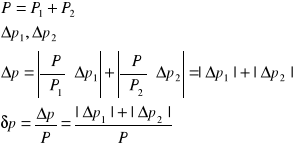
Pomiar rezystancji metodą techniczną, (za pomocą woltomierza i amperomierza).

Układ poprawnie mierzonego napięcia (U):

prąd płynący przez woltomierz Rv<<∞

Układ poprawnie mierzonego prądu (I):

Dla przyrządów analogowych:

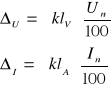
Dla przyrządów cyfrowych:

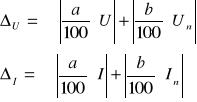
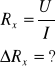
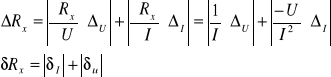
Np. Ex = ?

Δ_E = ?

p = -Δ_E

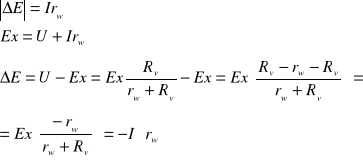
BŁĘDY PRZYPADKOWE (LOSOWE) to błędy zmieniające się w sposób nieprzewidziany zarówno co do wartości bezwzględnej, jak i znaku przy wykonywaniu dużej liczby pomiarów tej samej pewnej wielkości w warunkach pozornie niezmiennych.

Błędy te modeluje się za pomocą zmiennej losowej (jedna przyczyna --> różne skutki)

Wyeliminowanie błędu przypadkowego - stosujemy rachunek prawdopodobieństwa.

Zmienne losowe

(zmienna która przyjmuje wartości

z określonym prawdopodobieństwem)

dyskretna ciągła (dowolna wartość

(np. rzut monetą) z przedziału)

Rozkład zmiennej losowej X - prawdopodobieństwo przyjmowania przez zmienną losową wartości X.

Parametry charakteryzujące rozkład zmiennej losowej X:

- Dystrybuanta

- Funkcja gęstości prawdopodobieństwa

- Momenty centralne

Dystrybuanta

F(x)

F(x) = P(X ≤ x)

P - prawdopodobieństwo

Dystrybuantą nazywamy prawdopodobieństwo że zmienna X przyjmuje wartości równe lub mniejsze od X.

Na podstawie dystrybuanty można wyznaczyć prawdopodobieństwo, że a < x ≤ b, gdzie a < b i

a, b - dowolne liczby rzeczywiste

P(a < X ≤ b) = F(b)

zakres pomiarowy wybierany na przyrządzie

---