Nowoczesne Wysoko Pojemne Sieci Bezprzewodowe

z Dywersyfikacją Przestrzenną MIMO

J. PAWELEC

Abstract - The paper deals with new technique of signal transmission in wireless networks. It consists in forming many space channels between transmitter and receiver points, which facilitates a considerable growth of aggregate link capacity. The simple model of such transmission is given, which takes into account the essential environment factors, including non-selective fading. In a result the BER curves are produced for different normalized fading bandwidth BT, where B is Doppler shift and T - duration of signal symbol. In conclusion the high efficiency of new technology is emphasized, and some limitations specified such as high level of complexity and high cost. The obtained gain is also considerably lower than the prediction of a pure theory.

Streszczenie- Artykuł dotyczy nowej techniki transmisji informacji w sieciach bezprzewodowych. Polega ona na tworzeniu wielu kanałów przestrzennych między nadawcą i odbiorcą, co pozwala znacznie zwiększyć sumaryczną przepustowość łącza. Autor wprowadza prosty model takiej transmisji, w którym uwzględnia istotne czynniki środowiskowe, w tym nie-selektywne (płaskie) zaniki sygnału. W efekcie otrzymuje krzywe elementowej stopy błędów transmisji w funkcji stosunku mocy sygnał/szum dla parametrycznej zmiany znormalizowanego pasma zaników BT, gdzie B- pasmo koherencji (niestałości) zaników, 1/T -szybkość transmisji sygnału. We wnioskach autor potwierdza efektywność nowej technologii z jednoczesnym zastrzeżeniem, że faktyczne zaski są znacznie mniejsze od przewidywań teorii dla typowych warunków eksploatacji i że konieczne są duże nakłady środków w toku implementacji nowej technologii.

1. WPROWADZENIE

Komunikacja bezprzewodowa rozwija się z zawrotną szybkością. Mniej więcej co dwa lata podwaja się strumień informacji przesyłanej tą drogą. Powstają obawy, że za kilka lat może nastąpić regres wywołany zajęciem wszystkich możliwych fal i powstaniem dużych wzajemnych zakłóceń. Stan ten daje się już zauważyć w Stanach Zjednoczonych. Uczeni zaczęli w związku z tym szukać rozwiązań na polu nowych technologii. Potomek wielkiego Bella - Foschini wymyślił jeszcze w końcowych latach 90. technikę MIMO (multiple input- multiple output), która daje szansę zwiększenia przepustowości sieci proporcjonalną do liczby użytych anten, przy niezmienionej mocy i paśmie zajmowanych częstotliwości. Świat naukowy podchwycił ten pomysł z ogromnym zainteresowaniem. Na konferencjach telekomunikacyjnych nie mówi się prawie o niczym innym, tylko o MIMO (IEEE -VTC, IEEE-COM, MILCOM).

Niniejszy artykuł sprowadza problem nieco na ziemię. Wykazujemy w nim, w oparciu o obliczenia i symulacje, że znacząca poprawa jest możliwa, ale wymaga bardzo wielu dodatkowych zabiegów, które kosztują i dają w efekcie nie aż tak wielkie zyski, jakby to wynikało z czystej teorii. Koszty te należy jednak podjąć, bo nie ma innego lepszego wyjścia.

Prezentowany materiał nie był dotąd nigdzie publikowany, z wyjątkiem krótkiej zapowiedzi w IEEE Communications Letters [Paw10].

2. FOSCHINI I V-BLAST

Jeszcze na długo przed Foschinim uczeni przewidzieli możliwość zwiększenia przepustowości łączy na drodze dywersyfikacji przestrzennej, np. [Ost70]

(1)

gdzie ρ - średni stosunek sygnał/szum (SNR); I_M - macierz jednostkowa MxN; H - macierz prostokątna MxN; M - liczba anten odbiorczych; N - liczba anten nadawczych; H* - macierz transponowana hermitowska.

Elementami H są zmienne gaussowskie zespolone, kołowo symetryczne o wartości średniej 0 i wariancji 1 (z=x+jy, σ_X²/2+σ_Y²/2=1). Ponieważ składniki macierzy H są losowe, przeto także sama macierz i przepustowość stanowią zmienne losowe. Traktując zaniki sygnału na trasie propagacji jako funkcję odcinkowo-stałą (flat fading) i kodując kanał dla wielu takich odcinków, możemy c traktować jako wartość oczekiwaną przepustowości wg Shannona dla kanału ergodycznego. W praktyce posługujemy się dystrybuantą C.

Przykład

Rozważymy 3 układy MIMO zawierające kolejno po jednej, po dwie i po trzy anteny z każdej strony łącza. Niech zasięg łącza D=150m, odstępy między antenami d=1,5m, długość fali λ=15cm (2,4 GHz), stosunek mocy sygnału do szumu, SNR=10. Dla zachowania dokładnych relacji między trzema grupami wyników zastosujemy jednakowe ziarno generatora losowego seed 0 oraz jednakowe liczby losowań 10.000 wartości dla każdej ze zmiennych gaussowskich odpowiadających liczbie kanałów. Wynikiem próby będą odpowiednie dystrybuanty C - średnia, minimalna i maksymalna. Przy sumowaniu sygnałów w punktach odbiorczych uwzględniono różnice dróg i faz zgodnie z [Ges02]. Założono, że kanały są nie-skorelowane i nie podlegają jakimkolwiek szybkim zanikom.

Uzyskane rezultaty zamieszczono w tablicy I oraz na rys.1. Widać, zarówno z tablicy, jak i z rysunku, że średnia przepustowość C rośnie dość dokładnie liniowo wraz ze wzrostem liczby anten: 3, 6, 9 [b/sHz]. Co ważne, w miarę, jak rośnie liczba anten, kurczy się groźny obszar o bardzo małej przepustowości: 0.0004, 0,07, 1,06

Tablica I. Przepustowości C w funkcji liczby anten

Przepustowości [b/sHz]	M=N=1	M=N=2	M=N=3
Minimalna	0,0004	0,07	1,06
Średnia	2,91	5,45	8,54
Maksymalna	6,55	10,35	13,04

Wykresy rys.1 pokazują sumę przepustowości do określonej granicy, np.10 b/sHz (oś odciętych). Dla krzywej czerwonej M=N=3 uzyskujemy do tej granicy aż 90% ogólnej przepustowości. Na pozostałe 10% składają się 3 b/sHz (bo max=13 b/sHz). Są one przenoszone w seansach o bardzo dużej przepustowości, ale za to krótkotrwałych. Podobnie jest z początkiem krzywych. Ważny jest tzw. outage, czyli odcięcie (strata). Pokazuje ona z jaką najmniejszą przepustowością musimy się liczyć przez 1% czasu obserwacji. W danym przypadku jest to około 2 b/sHz.

Uzyskane wyniki odnoszą się do środowiska z zanikami powolnymi płaskimi Rayleigha oraz do stanu, kiedy odbiornik nie tylko rozróżnia poszczególne kanały transmisji, ale zna dokładnie ich chwilowe transmitancje h(t). Warto podkreślić, iż liczba indywidualnych kanałów rośnie z kwadratem liczby anten i że wszystkie one pracują na tej samej częstotliwości. Jest to więc zadanie niezwykle trudne. Okazuje się jednak, że można je rozwiązać i zapewnić przepustowość bliską (1).

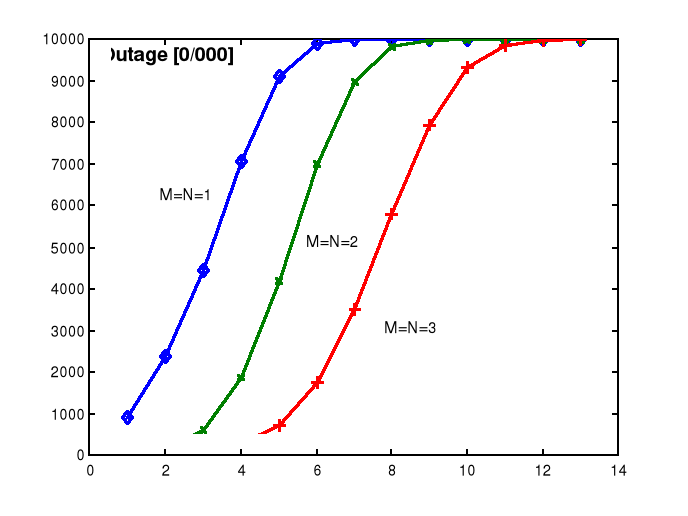
Rys.1. Przebiegi dystrybuant przepustowości C w zależności od liczby anten MIMO1,2,3

Należałoby obecnie opisać szczegółowo wynalazek Foschini'ego, tzw. V-BLAST (Vertical-Bell Laboratories Algorithm, Space-Time) [Fos96]. Objaśnienie pochłonęłoby jednak niemal cały artykuł i nie zadowoliło Czytelnika. Wobec takiej alternatywy ograniczymy się do przedstawienia innej prostszej wersji MIMO, danej niezależnie przez Alamouti'ego [Ala98].

3. MIMO ALAMOUTI'EGO

Schemat układu dano na rys.2. Mamy tu 2 anteny nadawcze (strzałki w górę) i 2 odbiorcze (strzałki w dół). W momencie t nadawane są sygnały, odpowiednio, s₀ i s_1,, a w następnym momencie t+T, gdzie T okres, te same sygnały, ale w odwrotnej kolejności i każdy w formie sprzężonej, przy czym s₁ dodatkowo ze zmianą fazy na przeciwną (-s^*₁). Taki układ umożliwia estymację i identyfikację obu sygnałów mimo ich emisji na tej samej częstotliwości w warunkach zaników i szumów.

Odpowiednie pary sygnałów r₀ i r₁ odbierane z kanałów h₀+h₁ w momentach t oi t+T oraz pary r₂ i r₃ odbierane z kanałów h₂+h₃ w tych samych momentach wynoszą

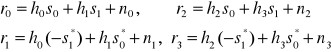
(2)

Na ich podstawie sumator buduje dwie estymaty sygnału i przekazuje je do detektora

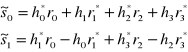
(3)

Detektor pracuje w oparciu o kryterium największej wiarygodności (ML)

(4)

gdzie {i,j} - alfabet sygnałów, i, j=1,2,...,M (dla BPSK i=1, j=2).

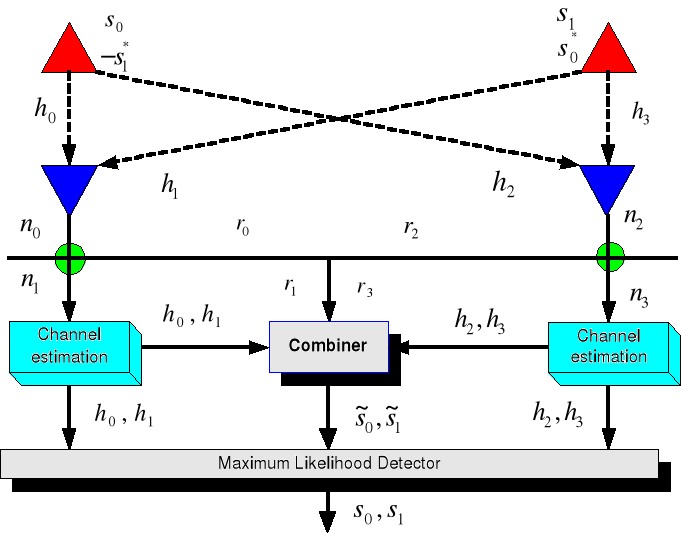
Rys.2. Ilustracja operacji sygnałowych w układzie MIMO2x2

Przedstawione rozwiązanie jest interesujące. Ma wszelako jedną słabą stronę: zakłada mianowicie jednakowe transmitancje w momentach t oraz t+T, h(t)=h(t+T), czyli przyjmuje, iż zaniki sygnałów na trasie propagacji są, po pierwsze płaskie (nie-selektywne) oraz, po drugie, są bardzo powolne względem szybkości transmisji 1/T.

Autor zadał sobie trud zbadania, co będzie, jeśli odstąpimy od tego założenia. Odpowiednie równania dla układu 2-antenowego (5-6) oraz 4-antenowego (7-8) dano poniżej. Indeks T przy transmitancjach oznacza stan dla momentów t+T

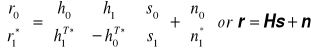
(5)

(6)

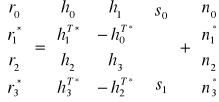
(7)

(8)

Dla obu przypadków obowiązuje to samo równanie kryterialne (9)

(9)

Jeśli jest spełnione, przyjmuje się, że odebrano sygnał s=s₀, w przeciwnym razie s=s₁.

W ostatnim równaniu przyjęto założenie, że aprioryczne prawdopodobieństwa stanów sygnału s₁ lub s₀ są jednakowe i równe 0.5. W związku z tym aposterioryczne prawdopodobieństwa błędów liczono tylko dla sygnału s₀.

Istotne jest równanie (6), które odbiega zasadniczo od (3a). Wartości h(t)=h oraz h(t+T)=h^T uzyskano w eksperymencie drogą dokładnego rozwinięcia efektu Dopplera, MEDS [Pat98]. Na ich podstawie wyliczana jest estymata (6), którą dalej porównuje się z sygnałem s₀ według kryterium największej wiarygodności (ML), równ. (9).

Wyniki modelowania procesów odbioru przedstawiono na rys. 3. Oryginalne krzywe Alamouti'ego dla h(t)=h(t+T) są przedstawione liniami pogrubionymi i oznaczone przez BT=0. Inne krzywe dotyczą stanu odejścia od tego założenia i przyjęcia wartości transmitancji h(t) zgodnie z MEDS. Stopień tego odejścia jest określony tzw. znormalizowanym pasmem zaników BT, gdzie B oznacza pasmo koherencji (odwrotność okresu względnej stałości). Na rys.3 pokazano dwie grupy krzywych, dla tzw. układu MISO (2 anteny nadawcze, jedna odbiorcza) oraz MIMO (po 2 anteny z każdej strony). Miarą jakości układu jest elementowa stopa błędów transmisji BER dla danego SNR.

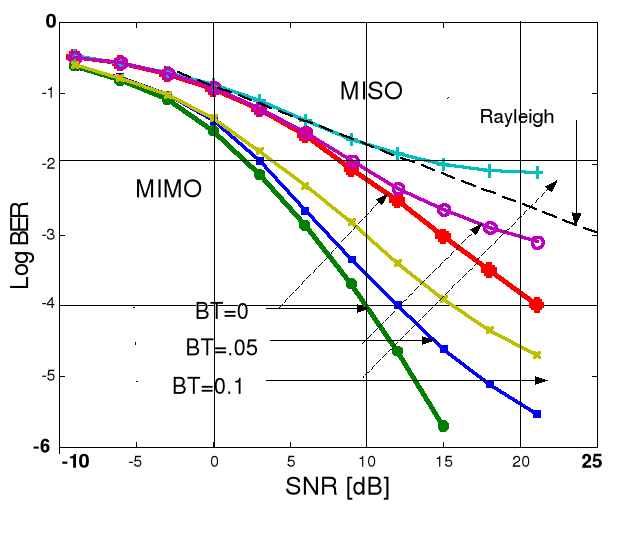
Rys.3. Przebieg stopy błędów dla MIMO/MISO w funkcji mocy w obecności zaników

Widzimy, że w miarę, jak wzrasta szybkość zaników BT, jakość pracy układu się pogarsza i przy pewnym stosunku SNR stopa przestaje reagować na podwyższenie mocy. Jest to wyraźnie widoczne dla układu MISO, gdzie powyżej SNR=10 dB stopa staje się gorsza, niż dla indywidualnego kanału Rayleigha. Dla MIMO2x2 możliwe jest jednak uzyskanie średniej stopy błędów 10^-4 za cenę niewielkiego zwiększenia mocy sygnału względem stanu bez zaników (ok. 6 dB). Zysk energetyczny wobec pojedynczego kanału Rayleigha na poziomie BER=10^-4 (niewidoczne na rysunku) wynosi wtedy około 20 dB, czyli 100 razy. Jest to wciąż duża wartość.

4. WNIOSKI

Systemy MIMO są opłacalne, bo zapewniają, albo znacznie większą średnią przepustowość łącza, proporcjonalnie do liczby użytych anten, albo odpowiednio mniejszą średnią stopę błędów w stosunku do indywidualnego kanału z zanikami Rayleigha. Zysk energetyczny dla 4-antenowego układu MIMO w warunkach umiarkowanie szybkich zaników płaskich (BT=0.1) wynosi blisko 100 razy względem indywidualnego kanału Rayleigha. Nowa technologia jest jednak złożona i kosztowna.

Badany model MIMO nie uwzględnia zaników selektywnych (nie płaskich), ale te można neutralizować drogą podziału pasma kanału technikami OFDM (orthogonal frequency division multiplexing). Model zakłada też, że transmitancje kanałów są znane i nie-skorelowane. Oba zagadnienia są rozwiązywalne znanymi technikami [Lam, Paw10]

LITERATURA

1962 P. Bello and B. Nelin, “ The Influence of Fading Spectrum on the Binary Error Probabilities of Incoherent and Differentially Coherent Matched Filter Receivers”, IRE Transactions on Communication Systems, June 1962

1964. Fisz Prawdopodobieństwo i statystyka matematyczna, PWN, Warszawa 1964

1970 D. Osteyee and I. Good, Information Weight of Evidence - the Singularity between Probability Measures and Signal Detection, Springer Verlag, New York 1970

1996 G. Foschini, “Layerd Space-Time Architecture for Wireless Communication in a Fading Environment when using Multi-element Antennas”, Bell Lab. Tech. J, 1996

1998. E. Biglieri, J. Proakis, S. Shamai, „Fading Channels: Information-Theoretic and Communications Aspects“, IEEE Tran. Information Theory, v.44, no. 6, October 1998

1998. J. Liu and R. Chen, “Sequential Monte Carlo Methods for Dynamic Systems”, Journal of the American Statistical Association, v. 93, no. 443, September 1998

1998. M. Patzold, U. Killat, F. Laune and Y. Li, “On the Statistical Properties of Deterministic Simulation Models for Mobile Fading Channels”, IEEE Transactions on. Vehicular Technology, v.47, no. 1, February 1998 (also IEEE-VTC, October 1999)

1998.S. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communicati-ons”, IEEE Journal on Selected Areas of Communications, October 1998

2002. D. Gesbert, “Outdoor MIMO Wireless Channels: Models and Performance”, IEEE-Transactions on Communications, December 2002

2002. J. Pawelec, Radio Communications - EMC problems, WPR 2002 (in Polish)

2002. Z. Yang and X. Wang, „A Sequential Monte Carlo Blind Receiver for OFDM Systems in Selective Fading Channels”, IEEE Trans. Signal Proc., February 2002

2004. A. Vielmon, Y. Li, and J. Barry, “Performance of Alamouti Transmitt Diversity over Time-Varying Rayleigh-Fading Channels”, IEEE Transactions on Wireless Communications, v.3, no.5, September 2004

2008. J. Pawelec, “Shannon Theory: Myths and Reality”, The Bulletin of the Polish Academy of Sciences, Techn. Sciences, no 4, 2008

2008. K. Kosmowski, „Symulacja korelacji wzajemnej zaników w systemach MIMO i jej wpływ na zysk odbioru”, Krajowe Sympozjum Telekomunikacji, Bydgoszcz, 2008

2010. J. Pawelec, “Performance of Alamouti's MISO and MIMO Systems over Flat Fading Channels with Crosscorrelation”, IEEE Comm. Letters, 2010 (in review)

2010. R. Lamare, and R. Sampaio-Neto, “Blind Adaptive MIMO Receivers for STBC DS-CDMA Systems in Multipath Channels using Constant Modulus Criterion”, IEEE Transactions on Communications, v. 58, no.1, January 2010

Zaniki dzielimy na selektywne i nie-selektywne, inaczej płaskie w zależności od stosunku pasma Dopplera do szybkości transmisji 1/T (nie-selektywne, to B_d<<1/T). W każdej grupie zaniki mogą być szybkie lub powolne, w zależności od stosunku pasma koherencji B_c do szybkości transmisji 1/T (powolne to B_c<<1/T)

Parametr BT=0,1 oznacza, że częstość zaników jest średnio 10 razy wolniejsza od szybkości transmisji sygnału 1/T.

---