I grupa
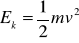
Energia kinetyczna w ruchu postępowym
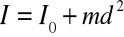
Twierdzenie Steinera
Io - moment bezwładności względem osi przechodzącej przez środek masy
I - moment bezwładności względem osi równoległej
d - odległość między osiami
m - masa bryły
Moment pędu
Prawo powszechnej grawitacji
Natężenie pola elektrycznego dla kuli
∫Eds=E(4πr2)=Qwew/ ε0, E=k·Q/R3·r
Kontrakcja długości
l0=l0'
, l0 długość poruszającego
się ciała, l0' długość ciała w spoczynku
β=v/c
Ruch harmoniczny prosty
równanie: m·d2x/dt2+kx=0,
rozwiązanie: x=Acos(ωt+δ)
Wahadło matematyczne - wyidealizowane ciało o masie punktowej m, zawieszone na cienkiej, nierozciągliwej nici. Wytrącone z równowagi waha się w płaszczyźnie pionowej pod wpływem siły ciężkości.
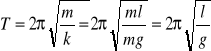
Prawo Gaussa dla pola elektrycznego
![]()
gdzie
E1 - jest wytwarzane przez Q1, a E2 przez Q2.
ၦcałk = (Q1/ၥ0) + (Q2/ၥ0) = (Q1 + Q2)/ၥ0
![]()
.
10.
gdzie
- SEM jest pracą na jednostkę ładunku wykonaną przy przeniesieniu ładunku wokół zamkniętej pętli (ၥ = W/q),
ၦ - strumień magnetyczny przechodzący przez tę pętlę.
11. Mmagnetycznym momentem
dipolowym nazywamy pole magnetyczne działające na ramkę
z prądem momentem skracającym obracając ją.
II grupa
Energia kinetyczna w ruchu obrotowym
E=½Iω2
Można to zapisać wzorem:
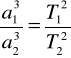
gdzie:
T1, T2 - okresy obiegu dwóch planet,
a1, a2 - wielkie półosie orbit tych planet
3 Moment siły
4.Prawo Coulomba
![]()
Siła oddziaływania dwóch ładunków q1 i q2 (naładowanych ciał)
5. Natężenie pola grawitacyjnego
![]()
- wewnątrz kuli
-zewnątrz kuli
![]()
6.Dylatacja czasu
Δt=Δt'
,
7. ruch harmoniczny tłumiony
m·d2x/dt2=-kx-k1·dx/dt,
k1 współczynnik oporu środka, czyli
d2x/dt2+k/m·x+k1/m·dx/dt=0 i k/m=ω0, k1/m=2β wtedy
d2x/dt2+ ω0x+2β·dx/dt=0,
x=x0e-βtcos(ω1t+α) gdzie β=k1/2m, ω1=√ω02-β2,
ω0=√k/m, (ω02> β2), tłumienie λ (T okres ruchu
harmonicznego tłumionego, δ dekrement tłumienia)
λ=x(t)/x(1+t)=eβT gdzie T=2π/ω i δ=lnλ=βT
8.Wahadło fizyczne
lr - długość zredukowana wahadła fizycznego, określa ona odległość takich dwóch osi (niesymetrycznie położonych względem środka ciężkości), wokół których wahadło waha się z jednakowym okresem.
9.Prawo Gaussa dla pola magnetycznego
wektor dS jest wektorem powierzchni,
współczynnikiem proporcjonalności jest przenikalność elektryczna próżni εo.
∇ · E - dywergencja natężenia pola elektrycznego,
ρ - gęstość ładunku.
10.Uogólnione prawo Ampera
∫Bdl= μ0(I+ ε0·∂ΦE/∂t)= μ0(I+IP), B indukcja magnetyczna,
dl element przewodnika, μ0 przenikalność magnetyczna,
I natężenie prądu, ε0 przenikalność dielektryczna,
ΦE strumień pola elektrycznego, IP prąd przesunięcia
Elektryczny moment dipolowy jest to wektorowa wielkość fizyczna charakteryzująca dipol elektryczny. Dipol jest układem dwóch ładunków o tych samych wartościach bezwzględnych, ale przeciwnych znakach
P=qd
![]()
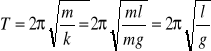
![]()
![]()
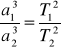
![]()
![]()
![]()
Wyszukiwarka