13. Testowanie hipotez dotyczących stałości wariancji składników zakłócających

Założenie o stałości wariancji jest jednym z założeń przyjmowanych w trakcie tworzenia modelu. Niespełnienie tego założenia powoduje, że oceny parametrów strukturalnych uzyskane MNK nie są już ocenami najlepszymi (o najmniejszych średnich błędach). W związku z tym oceny średnich błędów ocen uzyskane na podstawie macierzy
nie są poprawne, stąd wnioskowanie o istotności oddziaływania zmiennych na podstawie ocen MNK jest niewłaściwe.

Rozpatrzmy teraz możliwości weryfikacji hipotezy o stałości wariancji składników zakłócających modelu dla szeregów czasowych. Istnieje wiele testów, które mogą być wykorzystane do badania zmienności w czasie wariancji składników zakłócających. W trakcie wykładu omówione zostaną dwie z nich: test Goldfelda-Quandta oraz test mnożników Lagrange'a oraz jego wersja o rozkładzie Fishera-Snedecora.

We wszystkich testach hipoteza zerowa głosi, że wariancja składników zakłócających jest stała w czasie, co jest, jak pamiętamy, jednym z założeń liniowego modelu ekonometrycznego. Testy te różnią się natomiast hipotezami alternatywnymi. Zatem hipoteza o stałości wariancji będzie odrzucana na korzyść różnych możliwych procesów generujących składniki zakłócające o zmiennej wariancji.

13.1. Test Goldfelda-Quandta

Najpierw omówimy procedurę Goldfelda-Quandta, pozwalającą na weryfikację hipotezy o stałości wariacji, bez określania w hipotezie alternatywnej rodzaju heteroskedastyczności. Omawiać będziemy model dla szeregu czasowego zmiennej
:

. (13.1)

Rozważać będziemy układ hipotez:

. (13.2)

Intuicyjnym podejściem związanym z testowaniem stałości wariancji składników zakłócających modelu jest analiza reszt z oszacowania MNK parametrów modelu (13.1). Gdyby reszty z oszacowania MNK w miarę upływu czasu rosły, bądź malały, wtedy istniałyby przesłanki do odrzucenia hipotezy zerowej. Gdyby wartości reszt, co do modułu, były takiego samego rzędu, wtedy ich kwadraty byłyby również takiego samego rzędu, a zatem przemawiałoby za akceptacją hipotezy zerowej. W przypadku, gdy istniałoby przypuszczenie, że wariancja reszt zmienia się monotonicznie w ślad za wyróżnioną zmienną objaśniającą lub jej kwadratem, wtedy zaistniałaby konieczność uporządkowania reszt zgodnie z malejącymi, bądź rosnącymi wartościami tej zmiennej. Podobnie, gdyby rozpatrywać zależność wariancji reszt od oczekiwanego poziomu zmiennej endogenicznej, bądź kwadratu tej zmiennej, wtedy należałoby uporządkować reszty zgodnie z rosnącymi, bądź malejącymi wartościami teoretycznymi tej zmiennej.

Jeśli ciąg reszt, bądź uporządkowany ciąg reszt wykazywałby zmienną wariancję, wtedy naturalną koncepcją badania byłoby podzielenie szeregu czasowego zawierającego
elementów na dwie odrębne podpróby o równej liczebności i obliczenie dwóch wariancji reszt, na podstawie dwóch odrębnych oszacowań modelu. W przypadku, gdy
jest parzyste wtedy obie podpróby liczyłyby po
obserwacji. W przypadku, gdy
jest nieparzyste można pominąć środkową obserwację. Istotną wadą omawianej procedury jest jednak zmniejszenie liczby stopni swobody, wynikające z podzielenia próby na dwie części. W przypadku, gdy liczebność próby jest znaczna
, wyeliminowanie pewnej liczby środkowych obserwacji może zwiększyć moc testu Goldfelda_Quandta.

Jeśli założenie o stałości wariancji składników zakłócających jest prawdziwe, wtedy wariancje reszt obliczone dla dwóch podprób, nie powinny różnić się znacząco. Odwrotnie jest w przypadku, gdy wariancja składników zakłócających nie zmienia się w czasie. Wtedy wariancje reszt wyznaczone dla obu podprób powinny różnić się znacznie. Ponieważ oszacowania wariancji reszt otrzymuje się na podstawie dwóch niezależnych zbiorów reszt, zatem można w procedurze testującej wykorzystać statystykę Fishera-Snedecora, opartą na ilorazie wariancji reszt. Przykład modelu sprzedaży ilustruje zastosowanie tej procedury. Rozpatrzmy model liniowej tendencji rozwojowej, zapisany w postaci:

(13.3)

gdzie
oznacza wartość kwartalnej sprzedaży detalicznej w Polsce w mln złotych.

Rozpatrzymy obecnie podział szeregu czasowego liczącego 48 kwartałów z lat 1990-2001 na dwie równe podpróby, liczące po 24 obserwacje kwartalne oraz oszacowania parametrów modelu sprzedaży na ich podstawie. W konsekwencji zapiszemy:

, (13.4)

. (13.5)

W tablicy 13.1 zamieszczono wyniki oszacowań modelu tendencji rozwojowej sprzedaży. Widzimy, oszacowania parametrów strukturalnych, jak również oszacowania odchyleń standardowych reszt w obu podpróbach różnią się znacznie.

Tablica 13.1 Oszacowania parametrów modelu sprzedaży

Próba	Oszacowana postać modelu	Średni błąd reszt
1990Q1-2001Q4
1990Q1-1995Q4
1996Q1-2001Q4

Źródło: opracowanie własne

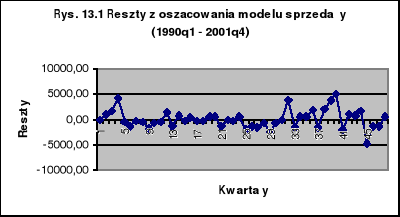
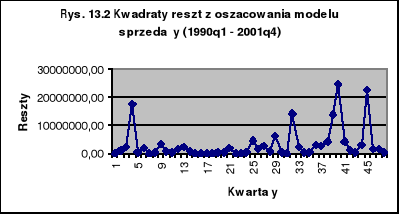
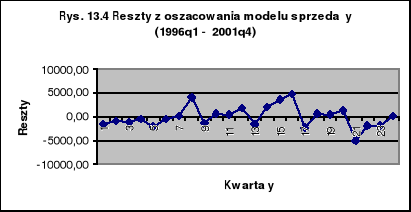
W tablicy 13.2 oraz na rysunkach 13.1 i 13.2 pokazano reszty z oszacowania MNK tego modelu. Widać wyraźnie, że od roku 1996 reszty są wyraźnie większe co do modułu, niż w latach 1990-1995. W szczególności pokazują to kwadraty reszt na rysunku 13.2.

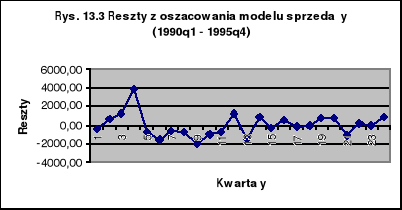
Na podstawie dwóch zbiorów reszt (zob. tablica 13.2 oraz rysunki 13.3, 13.4) wyznaczono wariancje reszt:

, (13.6)

. (13.7)

Jeżeli
, wtedy statystyka Fishera-Snedecora otrzymuje postać:

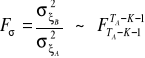
. (13.8)

Jeżeli natomiast
, wtedy wymieniona wyżej statystyka jest zapisana jako:

. (13.9)

W obu przypadkach duże wartości statystyki
świadczyć będą na korzyść hipotezy alternatywnej, małe jej wartości na korzyść hipotezy zerowej. W szczególności dla akceptowanego poziomu ryzyka
możemy podać następujące reguły podejmowania decyzji odnośnie do hipotezy zerowej:

- jeżeli zachodzi nierówność:

(13.10)

podejmujemy decyzję o odrzuceniu hipotezy zerowej na korzyść hipotezy alternatywnej,

- jeżeli zachodzi:

(13.11)

podejmujemy decyzję o braku podstaw do odrzucenia hipotezy zerowej.

Tablica 13.2 Reszty z oszacowania modelu sprzedaży

OBS.
1990Q1	1	-8,60	73,99	-439,88	193491,95	-	-
1990Q2	2	993,44	986923,43	597,92	357512,63	-	-
1990Q3	3	1549,30	2400330,49	1189,60	1415148,16	-	-
1990Q4	4	4219,30	17802492,49	3895,30	15173362,09	-	-
1991Q1	5	-495,70	245722,36	-783,94	614568,82	-	-
1991Q2	6	-1349,40	1820880,36	-1601,90	2566083,61	-	-
1991Q3	7	-403,29	162646,78	-620,02	384422,44	-	-
1991Q4	8	-554,70	307690,98	-735,66	541200,64	-	-
1992Q1	9	-1826,20	3335006,44	-1971,40	3886417,96	-	-
1992Q2	10	-845,45	714782,83	-954,90	911825,22	-	-
1992Q3	11	-631,53	398833,42	-705,22	497336,52	-	-
1992Q4	12	1312,30	1722131,29	1274,30	1623840,49	-	-
1993Q1	13	-1464,00	2143296,00	-1466,20	2149742,44	-	-
1993Q2	14	854,56	730274,16	888,15	788807,76	-	-
1993Q3	15	-356,19	126870,89	-286,84	82278,91	-	-
1993Q4	16	401,69	161357,11	506,80	256844,11	-	-
1994Q1	17	-261,35	68304,14	-120,49	14517,07	-	-
1994Q2	18	-218,44	47716,69	-41,82	1748,83	-	-
1994Q3	19	539,68	291255,80	752,06	565597,85	-	-
1994Q4	20	486,24	236427,39	734,38	539310,90	-	-
1995Q1	21	-1322,20	1748212,84	-1038,30	1078066,89	-	-
1995Q2	22	-175,40	30766,07	144,25	20809,42	-	-
1995Q3	23	-427,19	182495,48	-71,78	5152,21	-	-
1995Q4	24	464,44	215705,81	855,62	732078,91	-	-
1996Q1	25	-2132,30	4546703,29	-	-	-1585,60	2514127,36
1996Q2	26	-1309,50	1714790,25	-	-	-808,50	653664,81
1996Q3	27	-1622,00	2630884,00	-	-	-1166,80	1361422,24
1996Q4	28	-768,42	590472,98	-	-	-359,06	128924,87
1997Q1	29	-2480,40	6152384,16	-	-	-2116,80	4480842,24
1997Q2	30	-663,48	440204,91	-	-	-345,72	119522,73
1997Q3	31	-114,10	13017,97	-	-	157,86	24920,13
1997Q4	32	3753,40	14088011,56	-	-	3979,60	15837216,16
1998Q1	33	-1513,50	2290682,25	-	-	-1333,20	1777422,24
1998Q2	34	485,73	235931,88	-	-	620,28	384749,39
1998Q3	35	473,45	224159,54	-	-	562,21	316076,94
1998Q4	36	1739,80	3026904,04	-	-	1782,70	3178019,29
1999Q1	37	-1676,30	2809981,69	-	-	-1679,10	2819376,81
1999Q2	38	2041,90	4169355,61	-	-	1993,30	3973244,89
1999Q3	39	3722,10	13854028,41	-	-	3627,70	13160207,29
1999Q4	40	4954,20	24544097,64	-	-	4813,90	23173633,21
2000Q1	41	-2058,90	4239069,21	-	-	-2244,90	5039576,01
2000Q2	42	995,86	991743,31	-	-	764,01	583705,63
2000Q3	43	713,23	508697,75	-	-	435,57	189723,32
2000Q4	44	1700,80	2892720,64	-	-	1377,40	1897230,76
2001Q1	45	-4744,10	22506484,81	-	-	-5113,40	26146859,56
2001Q2	46	-1302,00	1695204,00	-	-	-1717,10	2948432,41
2001Q3	47	-1306,80	1707726,24	-	-	-1767,70	3124763,29
2001Q4	48	630,10	397026,64	-	-	123,44	15236,42
			3307619,13		1563643,90		5174949,91

Źródło: opracowanie własne

W rozpatrywanym przez nas obecnie przykładzie modelu sprzedaży, wariancja reszt wyznaczona na podstawie drugiej podpróby jest przeszło trzykrotnie większa niż wariancja reszt dla próby zawierającej pierwsze 24 kwartały. Łatwo sprawdzić, że wariancje reszt wynoszą:

;
.

W konsekwencji statystyka Fishera-Snedecora otrzymuje wartość:

.

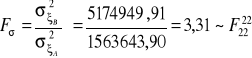
Wartość krytyczna, pochodząca z rozkładu Fishera-Snedecora dla poziomu istotności
, wynosi
. Ponieważ prawdziwa jest nierówność:

zatem podejmujemy decyzję o odrzuceniu hipotezy zerowej o stałości wariancji, na rzecz hipotezy alternatywnej, że wariancja w drugim podokresie jest większa niż w pierwszym.

13.2. Test mnożników Lagrange'a

Rozważmy obecnie zapisany niżej układ hipotez:

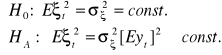
. (13.12)

W hipotezie zerowej zakładamy, że spełnione jest założenie klasycznego modelu liniowego. W hipotezie alternatywnej natomiast zakładamy, że wariancja składników zakłócających zmienia się w czasie w ślad za zmianami oczekiwanego poziomu zmiennej endogenicznej, konkretnie proporcjonalnie do kwadratu wartości oczekiwanej. Wariancja
jest traktowana w hipotezie alternatywnej jako ,,czynnik skalujący''. Zauważmy, że oczekiwana wartość zmiennej endogenicznej nie jest znana. Po oszacowaniu parametrów strukturalnych modelu ekonometrycznego możemy wyznaczyć wartość teoretyczną zmiennej endogenicznej, która jest oszacowaniem oczekiwanej wartości zmiennej endogenicznej. Dla zaobserwowanych w próbie wartości zmiennych objaśniających wartość ta jest obliczana, jak pamiętamy, za pomocą wzoru:

, (13.13)

przy czym, choć nie zaznaczono tego w zapisie, model może być zarówno statyczny jak i dynamiczny.

Test mnożników Lagrange'a w wersji o rozkładzie
oraz w wersji o rozkładzie Fishera-Snedecora oparty jest na analizie następującej relacji pomocniczej:

, (13.14)

gdzie:
jest resztą z oszacowania MNK liniowego modelu ekonometrycznego,
,
są nieznanymi parametrami,
jest natomiast składnikiem zakłócającym o stałej wariancji.

Testy mnożników Lagrange'a są testami istotności współczynnika
w relacji (13.14). Jeśli hipoteza zerowa, że
jest prawdziwa, to model pomocniczy redukuje się do
, co oznacza, że kwadraty reszt oscylują wokół stałej. Świadczy to na korzyść hipotezy zerowej o stałości wariancji składników zakłócających. Odrzucenie hipotezy zerowej, że
oznacza, że kwadraty reszt zmieniają się w ślad za zmianami poziomów zmiennej endogenicznej. Daje to podstawy do odrzucenia hipotezy o stałości wariancji składników zakłócających na korzyść hipotezy alternatywnej.

W teście mnożników Lagrange'a o rozkładzie
porównywać będziemy sumy kwadratów reszt MNK dla modelu (13.14) w warunkach prawdziwości hipotezy zerowej i w warunkach jej odrzucenia. Ponieważ w relacji (13.14) występuje tylko jedna zmienna objaśniająca, zatem porównywać będziemy sumę kwadratów reszt w warunkach prawdziwości hipotezy zerowej tj. dla modelu
, którą oznaczymy
z sumą kwadratów reszt dla modelu
, tj. gdy hipoteza zerowa jest odrzucona, którą oznaczymy
. Na podstawie rozważań zawartych w rozdziale szóstym, stwierdzamy, że:

.

Statystką o asymptotycznym rozkładzie
jest:

(13.15)

natomiast jej wersją o rozkładzie Fishera-Snedecora jest

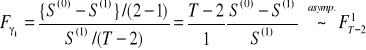
. (13.16)

Zauważmy, że z konstrukcji relacji pomocniczej wynika, że suma kwadratów
będzie miała postać
, gdzie
jest średnią arytmetyczną kwadratów reszt.

Licznik obu statystyk określa spadek sumy kwadratów reszt modelu pomocniczego (13.14) na skutek dołączenia do modelu
zmiennej
. Jeśli kwadraty reszt nie będą stałe, ale zmieniać się będą w ślad za zmianami poziomu zmiennej endogenicznej, wtedy zmienna
będzie w istotny sposób objaśniać ich zmienność, a zatem spadek sumy kwadratów reszt będzie znaczny. Jeśli kwadraty reszt będą względnie stałe, zmienna
będzie nieistotna i spadek sumy kwadratów reszt będzie niewielki. Małe wartości obu statystyk przemawiać będą na korzyść hipotezy zerowej. Duże ich wartości przemawiać będą za jej odrzuceniem, na korzyść hipotezy alternatywnej, że
.

Reguły podejmowania decyzji odnośnie do hipotezy zerowej w (13.12) są następujące:

• jeżeli
  (
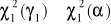
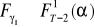
  ), to nie ma podstaw do odrzucenia hipotezy zerowej, że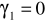
  , możemy powiedzieć, wariancja składników zakłócających jest stała w czasie,

• jeżeli
  , (
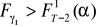
  ), hipoteza zerowa jest odrzucana na rzecz
  , zatem wariancja składników zakłócających zmienia się wraz ze zmianami poziomów zmiennej endogenicznej.

Symbolami
oraz
oznaczono wartości krytyczne pochodzące odpowiednio z rozkładów
oraz Fishera-Snedecora dla zaznaczonej liczby stopni swobody i akceptowanego poziomu ryzyka
.

W tablicy 13.3 podano wyniki testowania hipotezy zerowej o stałości wariancji składników zakłócających w jedno- i w dwuczynnikowym modelu kosztów całkowitych. Dla obu modeli zarówno statystyki
jaki i
są małe. Żeby odrzucić hipotezę zerową trzeba by przyjąć ryzyko rzędu 0,5- 0,6, co podano w nawiasach pod wartościami statystyki w tablicy 13.3. Zatem dla rozsądnych, bliskich zeru poziomów istotności podejmować będziemy decyzje o braku podstaw do odrzucenia hipotezy zerowej.

Tablica 13.3 Badanie stałości wariancji składników zakłócających w modelach kosztów

Model

Źródło: opracowanie własne

14. Test normalności składników zakłócających

Testowanie hipotezy zerowej dotyczącej normalności rozkładów składników zakłócających modelu należy do najważniejszych etapów weryfikacji statystycznej modelu. Statystyki wykorzystywane w procedurach testowania modelu ekonometrycznego, mają rozkłady należące do rodziny związanej z rozkładem normalnym (rozkład t-Studenta, rozkład
, rozkład Fishera-Snedecora), jeżeli składniki zakłócające
mają rozkłady normalne. Jeśli odrzucamy hipotezę o normalności składników zakłócających, poddajemy w wątpliwość wyniki testowania wszystkich hipotez. Podobnie jak to miało miejsce w poprzednich procedurach testujących, również obecnie będziemy weryfikować hipotezy dotyczące składników zakłócających na podstawie reszt z oszacowania MNK parametrów modelu. Rozważać będziemy zatem układ hipotez:

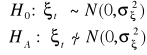
. (14.1)

Statystyką, którą wykorzystywać będziemy do sprawdzenia tej hipotezy nazywana jest statystyką Jarque-Bery (
). W przypadku, gdy w modelu występuje wyraz wolny, a zatem suma reszt i średnia reszt z oszacowania MNK są równe zero, statystyka ta definiowana jest następująco:

, (14.2)

gdzie:
- współczynnik skośności,
- współczynnik kurtozy,
,
- próbkowy moment centralny reszt z oszacowania MNK.

Dla rozkładu normalnego zachodzi równość:
. Jeżeli
- oznacza to skośność prawostronną rozkładu, gdy
- skośność lewostronną. Dla rozkładu normalnego zachodzi ponadto
. Jeżeli
oznacza to zwykle dla rozkładów jednomodalnych występowanie tzw. ,,pogrubionych ogonów''. Jeżeli natomiast
wtedy zwykle mówimy o występowaniu ,,zbyt cienkich ogonów'' rozkładu.

Jeśli rozkład reszt jest normalny, wtedy statystyka
przybiera wartości bliskie zeru. Jeśli rozkład reszt odbiega od normalnego, wskutek skośności albo spłaszczenia odbiegającego od normalnego, wtedy wartości tej statystyki przybierać będą duże wartości dodatnie.

Jeśli składniki losowe mają rozkłady normalne, wtedy statystyka
ma rozkład:

(14.3)

o dwóch stopniach swobody.

Reguła podejmowania decyzji jest następująca:

• jeżeli wartość statystyki
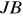
  jest ,,mała'', w szczególności nie większa od wartości krytycznej rozkładu dla założonego poziomu ryzyka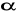
  , tj.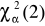
  

to nie ma podstaw do odrzucenia hipotezy zerowej, składniki zakłócające modelu mają

rozkłady normalne,

• jeżeli wartość statystyki
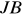
  jest ,,duża'', w szczególności większa od wartości krytycznej rozkładu dla założonego poziomu ryzyka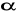
  , tj.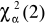
  

to hipotezę zerową odrzucamy na korzyść alternatywnej, że składniki zakłócające modelu nie mają

rozkładów normalnych.

W tablicy 14 podano wartości statystyki
dla dwóch modeli kosztów całkowitych. W obu przypadkach wartości statystyki
są tak małe, że pozwalają na odrzucenie hipotezy zerowej dopiero dla ryzyka rzędu 0,6. Zatem dla poziomów istotności bliskich zera podejmiemy decyzję o braku podstaw do odrzucenia hipotezy zerowej.

Tablica 14 Badanie normalności rozkładu składników zakłócających w modelach kosztów

Model

Źródło: opracowanie własne

Składniki zakłócające, które mają stałe w czasie wariancje nazywać będziemy homoskedastycznymi, natomiast te, których wariancje są zmienne w czasie heteroskedastycznymi.

Będziemy o tym mówić na wykładzie poświęconemu uogólnionej metodzie najmniejszych kwadratów.

Zob. G.S. Maddala, Introduction to Econometrics, str. 201-211.

Zob. S.M.Goldfelda, R.M. Quandt, Some Tests for Homoscedasticity, Journal of The American Statistical Association, 1965, vol. 60, str. 539-547.

Zob. M.H.Pesaran, B.Pesaran, Working with Microfit 4.0, Oxford University Press, Oxford 1997, str. 351.

Zob. H. Theil, Zasady ekonometrii, PWN, Warszawa 1979, str. 210.

W trakcie wykładu poświęconego testowaniu stabilności prognostycznej modelu powrócimy do tego przykładu.

Zobacz nierówność (6.52) w punkcie (6.3) wykład 6.

C.M.Jarque, A.K.Bera, Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals, Economic Letters, vol. 6, str. 255-259.

Tadeusz W.Bołt, Wykłady z ekonometrii

159

---