Strop gęstożebrowy

OBLICZENIE STROPU FERT 60

Zaprojektować strop typu FERT 60 nad piwnicą w budynku jednorodzinnym o rozpiętości
w świetle ścian: Belka nr 1: 3,05 m; Belka nr 2: 2,45 m.

Dane:

BELKA NR 1:

- rozpiętość stropu w świetle

- rozstaw żeber

- wysokość pustaka

- grubość płyty nadbetonu

- strop swobodnie podparty, współczynnik

- Beton klasy B20 o

- warunki środowiskowe suche, wnętrze budynku o niskiej wilgotności powietrza - klasa XC1,

- stal klasy A-III o znaku gatunku 34 GS i
oraz

BELKA NR 2:

- rozpiętość stropu w świetle

- rozstaw żeber

- wysokość pustaka

- grubość płyty nadbetonu

- strop swobodnie podparty, współczynnik

- Beton klasy B20 o

- warunki środowiskowe suche, wnętrze budynku o niskiej wilgotności powietrza - klasa XC1,

- stal klasy A-III o znaku gatunku 34 GS i
oraz

Układ warstw w stropie:

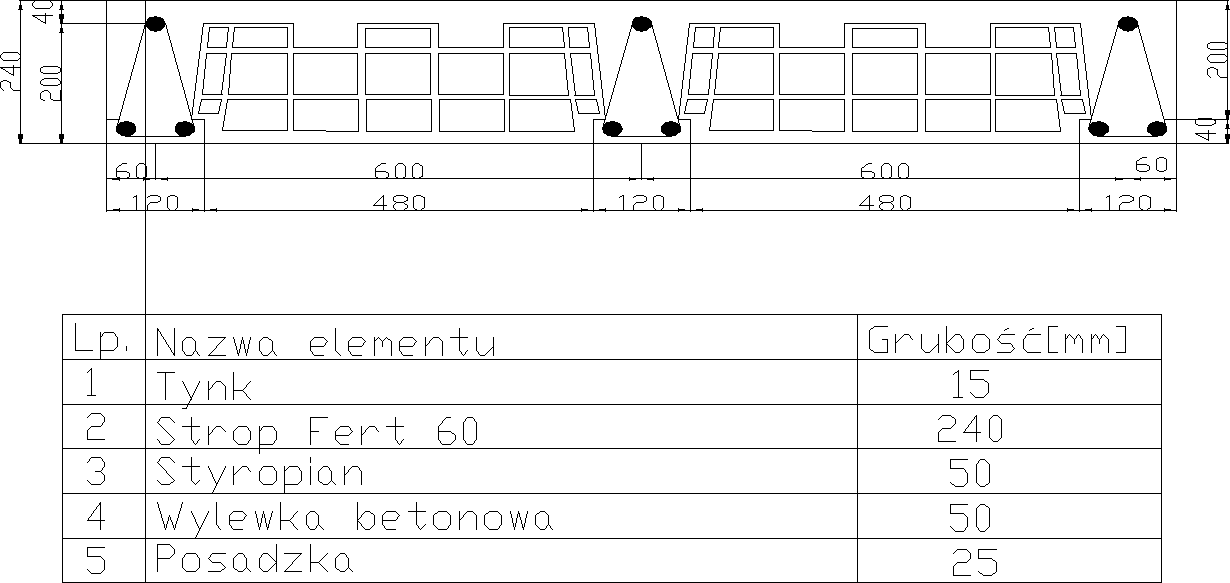
Zestawienie obciążeń na belkę nr 1:

Rodzaj obciążenia: stałe g:	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
Płytki ceramiczne o grubości 25mm
Gładź cementowa grubości 50mm
Styropian grubości 50mm
Strop FERT 60
Tynk cementowo -wapienny grubości 15mm
RAZEM
Rodzaj obciążenia: zmienne:	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
- zmienne technologiczne
- obciążenie od dwóch wymianów
RAZEM g+p+q

Zestawienie obciążeń na belkę nr 2:

Rodzaj obciążenia: stałe g:	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
Parkiet dębowy grubości 25mm
Gładź cementowa grubości 50mm
Styropian grubości 50mm
Strop FERT 60
Tynk cementowo -wapienny grubości 15mm
RAZEM
Rodzaj obciążenia: zmienne:	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
- zmienne technologiczne
- obciążenie od ścianki działowej grubości 120 mm
RAZEM g+p+q

Schemat statyczny belki nr1

Rodzaj obciążenia:	Wartości charakterystyczne	Współczynnik obciążenia	Wartości obliczeniowe
- obciążenie stałe
- zmienne technologiczne
RAZEM
Rodzaj obciążenia:	Wartości charakterystyczne		Wartości obliczeniowe
- obciążenie od dwóch wymianów

Schemat statyczny belki nr 2

Rodzaj obciążenia:	Wartości charakterystyczne	Współczynnik obciążenia	Wartości obliczeniowe
- obciążenie stałe
- zmienne technologiczne
- obciążenie od ścianki działowej
RAZEM

Schemat obciążeń belki nr 1 oraz wykresy sił wewnętrznych:

OBCIĄŻENIA:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])

------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------

Grupa: A "Stałe g" Stałe γf= 1,20

1 Liniowe 0,0 3,350 3,350 0,00 3,17

Grupa: B "Zmienne technologiczne p" Zmienne γf= 1,40

1 Liniowe 0,0 1,080 1,080 0,00 3,17

Grupa: C "Obciążenie od wymianów q" Stałe γf= 1,10

1 Skupione 0,0 0,347 0,37

1 Skupione 0,0 0,347 0,49

------------------------------------------------------------------

MOMENTY:

TNĄCE:

SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 9,441 0,000

0,50 1,582 7,136* -0,075 0,000

1,00 3,175 0,000 -8,886 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

Schemat obciążeń belki nr 2 oraz wykresy sił wewnętrznych:

OBCIĄŻENIA:

OBCIĄŻENIA: ([kN],[kNm],[kN/m])

------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------

Grupa: A "Stałe g" Stałe γf= 1,20

1 Liniowe 0,0 3,350 3,350 0,00 2,57

Grupa: B "Zmienne technologiczne p" Zmienne γf= 1,40

1 Liniowe 0,0 1,080 1,080 0,00 2,57

Grupa: C "Od ścianki działowej q" Zmienne γf= 1,20

1 Liniowe 0,0 5,400 5,400 0,00 2,57

------------------------------------------------------------------

MOMENTY:

TNĄCE:

SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -0,000 15,465 0,000

0,50 1,287 9,956* 0,000 0,000

1,00 2,575 -0,000 -15,465 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

Przekrój obliczeniowy żebra stropu FERT 60

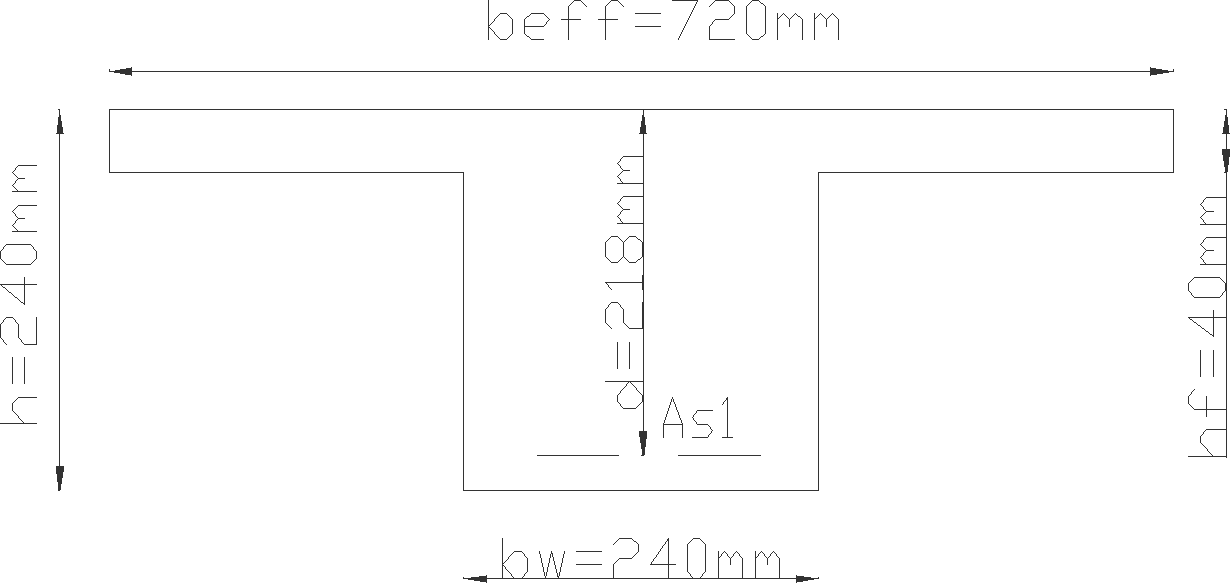
W obu belkach otulenie dla stali zbrojeniowej stanowi kształtka ceramiczna o grubości
, pręty zbrojenia belek o średnicy 8mm (w sumie 4 pręty, ponieważ jest to belka podwójna). Przy tych założeniach wysokość użyteczna przekroju wynosi:

Strefa ściskana:

A moment zginający przenoszony przez przekrój
wynosi:

- przekrój belki nr1 oraz belki nr 2 są przekrojami pozornie teowymi.

Wartości współczynnika
:

Dla belki nr 1 -

Dla belki nr 2 -

Dla obliczonego pola przekroju zastosowano 4 pręty o średnicy 8mm każdy:

Sprawdzenie warunku:

Warunek jest spełniony dla belki nr 1 oraz dla belki nr 2

Sprawdzanie konieczności obliczenia zbrojenia na ścinanie oraz szerokości rozwarcia rys ukośnych:

Wartość siły poprzecznej wynosi:

Dla belki nr 1:

- odczytano z wykresu

Ponieważ

zatem nie trzeba liczyć zbrojenia na ścinanie i szerokości rozwarcia rys ukośnych.

Dla belki nr 2:

- odczytano z wykresu

Ponieważ

zatem nie trzeba liczyć zbrojenia na ścinanie i szerokości rozwarcia rys ukośnych.

Sprawdzanie szerokości rys prostopadłych:

Dla środowiska klasy 1
. Ponieważ strop projektowany jest w budynku mieszkalnym, to

Belka nr 1:

Wartość charakterystyczna obciążenia belki nr 1 w kombinacji obciążeń długotrwałych wynosi:

MOMENTY OD OBCIĄŻEŃ DŁUGOTRWAŁYCH:

Naprężenia
w zbrojeniu rozciąganym wynoszą:

i spełniony jest warunek

Dla przyjętego zbrojenia
i
można stosować pręty do średnicy 32mm. Ponieważ przyjęto pręty średnicy 8mm, to bez szczegółowych obliczeń można stwierdzić, że dopuszczalna szerokość rozwarcia rys nie będzie przekroczona.

Belka nr 2:

Wartość charakterystyczna obciążenia belki nr 2 w kombinacji obciążeń długotrwałych wynosi:

MOMENTY OD OBCIĄŻEŃ DŁUGOTRWAŁYCH:

Naprężenia
w zbrojeniu rozciąganym wynoszą:

i spełniony jest warunek

Dla przyjętego zbrojenia
i
można stosować pręty do średnicy 12mm. Ponieważ przyjęto pręty średnicy 8mm, to bez szczegółowych obliczeń można stwierdzić, że dopuszczalna szerokość rozwarcia rys nie będzie przekroczona.

Sprawdzanie ugięcia:

Belka nr 1

Z normy PN-B-03264:2002 (tab.13) odczytano dla
, betonu klasy B15 i naprężeń

maksymalne
, które wynosi 24

Uwzględniając obliczoną wartość naprężeń
, obliczono wartość

Ponieważ wartość ta jest większa od wartości obliczonej dla belki nr 1, ugięcie stropu nie przekroczy wartości granicznej.

Belka nr 2

Z normy PN-B-03264:2002 (tab.13) odczytano dla
, betonu klasy B15 i naprężeń

maksymalne
, które wynosi 24

Uwzględniając obliczoną wartość naprężeń
, obliczono wartość

Ponieważ wartość ta jest większa od wartości obliczonej dla belki nr 2, ugięcie stropu nie przekroczy wartości granicznej.

Nadproże okienne

OBLICZENIE NADPROŻA OKIENNEGO Z BELEK PREFABYKOWANYCH ŻELBETOWYCH TYPU L

Nadproże znajduje się na ścianie zewnętrznej budynku. Otwór okienny ma szerokość
w świetle ściany 1,20 m, zatem
. Ściana wykonana jest w bloczków silikatowych BSD 250. Na ścianie na której znajduje się projektowane nadproże, opiera się strop
gęstożebrowy FERT 60 o rozpiętości modularnej 3,30 m. Obciążenie obliczeniowe dla stropu wynosi (tak jak w Belce nr 1 wyżej zwymiarowanej)
. Wstępnie przyjęto 3 belki nadprożowe typu L-19.

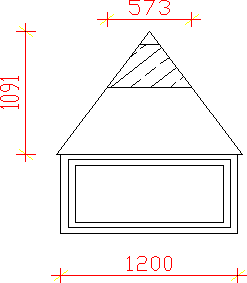
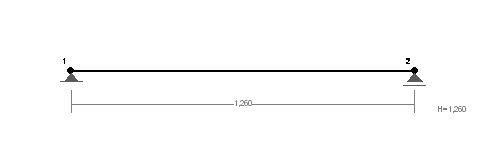
ZESTAWIENIE OBCIĄŻEŃ:

Rodzaj obciążenia: stałe g:	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
Mur z Silikatów BSD 250 grubości 250mm
Ściana osłonowa Silka 1NF grubości 120mm
Styropian grubości 160mm
Obciążenie od stropu
Tynk cementowo -wapienny grubości 15mm x2
RAZEM
Rodzaj obciążenia	Obciążenie charakterystyczne	Współczynnik obciążenia	Obciążenie obliczeniowe
Wieniec żelbetowy
Trzy belki nadprożowe typu L-19

Powierzchnia muru z Silikatów BSD 250, z której przypada obciążenie na nadproże wynosi:

- bez powierzchni wieńców. Powierzchnia ściany osłonowej z Silki 1NF, z której przypada obciążenie na nadproże wynosi:
.

Obciążenie przypadające od muru z Silikatów BSD 250:

Obciążenie przypadające od ściany osłonowej z Silki 1NF:

Obciążenie przypadające od stropów:

Obciążenie zastępcze od stropów i murów:

Obciążenie zastępcze całkowite przypadające na nadproże:

OBCIĄŻENIA:

MOMENTY:

Wstępnie przyjęto z tabeli 5.2 trzy belki N/180

Belka N/180 posiada zbrojenie w postaci 2 prętów o średnicy 6 mm, o polu przekroju

. Dla tak przyjętego nadproża sprawdzono jego nośność
zgodnie z normą
PN-B-03264:2002. Przyjęto
i klasę betonu B20, dla którego
. Grubość otulenia zbrojenia przyjęto c =15 mm, strzemiona o średnicy 4,5 mm, pręty zbrojenia żeber o średnicy 10 mm i dopuszczalną odchyłkę otuliny o Δh = 5mm. Przy tych założeniach wysokość użyteczna przekroju wynosi:

Stopień zbrojenia wynosi:

Na tej podstawie odczytano
dla stali 34GS

Nośność pojedynczej belki wynosi:

Ponieważ przyjęto trzy belki, zatem sumaryczna nośność wynosi:

Stan graniczny nośności dla przyjętego nadproża jest spełniony.

Przyjęto zatem 3 belki nadprożowe L-19 N/180

Ściany murowane

OBLICZENIE NOŚNOŚCI ŚCIANY MUROWANEJ ZEWNĘTRZNEJ I WEWNĘTRZNEJ

Ściana zewnętrzna i wewnętrzna wykonana jest z bloczków silikatowych BSD 250 klasy 20 na zaprawie zwykłej M10. Stropy w budynku są gestożebrowe FERT 60. Budynek zlokalizowany jest
w Krakowie, w I strefie wiatrowej. Przyjęto przegubowy model obliczeniowy.

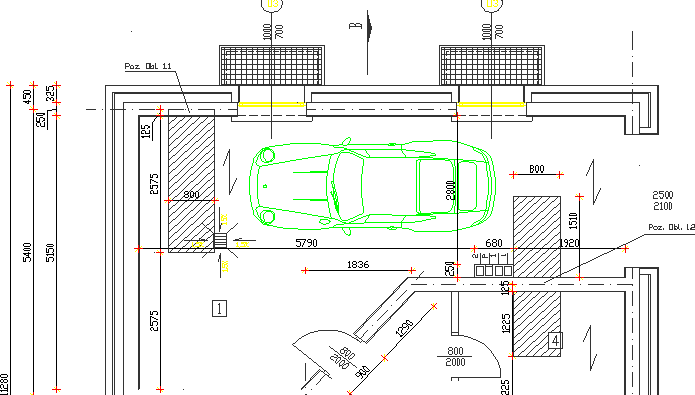
Rzut Piwnicy:

1. OBLICZENIE FILARA W ŚCIANIE ZEWNĘTRZNEJ

Przyjęto:

• Ciężar własny muru:
  ,

• Wytrzymałość charakterystyczna muru na ściskanie :
  ,

• Współczynnik bezpieczeństwa dla kategorii A wykonania robót na budowie
  ,

• Wymiary filara:
  ,

• Szerokość pasma, z którego przekazywane jest obciążenie na filar na wszystkich kondygnacjach:
  ,

• Grubość muru:
  ,

• Szerokość wieńca:
  ,

• Wysokość ściany w świetle stropów:
  ,

• Rozpiętość stropu w świetle ścian:
  .

Zestawienie obciążeń:

- obciążenie z dachu:
. Krokwie rozstawione są co 0,88m. Zatem siła przekazywana
z murłatu na ścianę wynosi:

- obciążenie od stropów:
. Powierzchnie obciążenia stropami nad piwnicą i parterem są sobie równe i wynoszą:

Do obliczeń przyjęto na poddaszu obciążenie użytkowe jak dla kondygnacji mieszkalnych.

- reakcje ze stropów wynoszą:

od stropu nad parterem:

od stropu nad piwnicą:

- ciężar ścian:

• ciężar własny muru wynosi :
  ,

• ciężar tynku cem. -wap. (jednostronnego) wynosi:
  

• ciężar własny ściany wynosi:
  

Powierzchnia obciążająca mur:

Siły skupione od ciężaru ścian:

- obciążenia budynku wiatrem:

Wymiary budynku:

Zatem:

Założono, ze budynek murowany jest niepodatny na dynamiczne działanie wiatru i przyjęto

Obciążenie obliczeniowe wywołane działaniem wiatru (kolejno parciem i ssaniem) wynosi:

Bardziej niekorzystne jest ssanie wiatru, zatem:

Moment obliczeniowy dla modelu przegubowego wynosi:

Łączne obciążenie przypadające na wieniec nad filarem w piwnicy, bez redukcji obciążenia użytkowego wynosi:

Obciążenie całkowite w piwnicy:

Określenie smukłości filara

Do określenia smukłości filara przyjęto:

stropy żelbetowe, konstrukcja usztywniona przestrzennie w sposób eliminujący przesuw poziom, rozstaw ścian usztywniających ścianę z filarem

Zatem z warunku
, wynika, że w ścianach występuje usztywnienie u góry i u dołu oraz usztywnienie wzdłuż jednej krawędzi pionowej.
Stąd:

Wysokość efektywna ściany wynosi:

Smukłość ściany spełnia zatem warunek:

Określenie wytrzymałości muru

Dla pustaka klasy 20 oraz zaprawy klasy M10 -

Pole przekroju elementu konstrukcji murowej wynosi:

Zatem

Wytrzymałość obliczeniowa muru wynosi:

Sprawdzanie stanu granicznego nośności filara

Do obliczeń przyjęto model przegubowy ze względu na brak odpowiedniego zbrojenia górnego
w węzłach-złączach służących do przeniesienia momentów podporowych. Miejsce przyłożenia sił
w modelu przegubowym pokazano na rysunku:

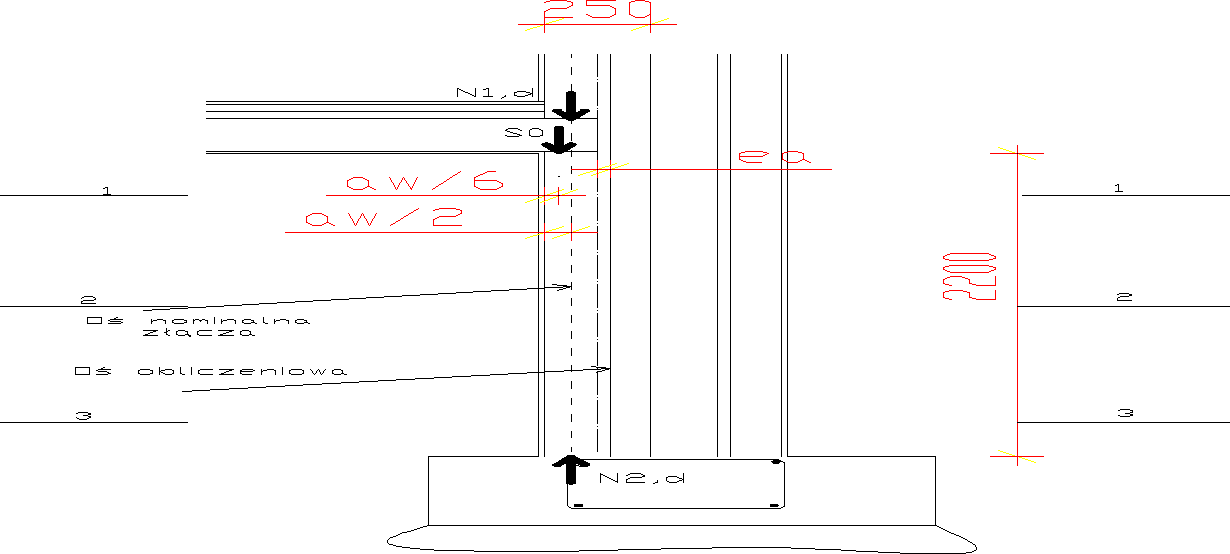
Mimośród przypadkowy:

W przekrojach 1-1 i 2-2 momenty wynoszą:

W przekrojach 1-1, 2-2 mimośrody wynoszą:

W przekrojach 1-1 i 2-2 współczynniki redukcyjne
wynoszą:

W przekrojach 1-1 i 2-2 nośności ściany wynoszą:

Stan graniczny nośności w przekrojach 1-1 i 2-2 nie jest przekroczony.

W przekroju 3-3 mimośród wynosi:

Cecha sprężystości muru wykonanego z bloków BSD 250 wynosi:
, a cecha sprężystości dla tego muru pod obciążeniem długotrwałym wynosi:
.

W przekroju 3-3 dla:

Zatem z tabeli:

W przekroju 3-3 nośność ściany wynosi:

Na podstawie przeprowadzonych obliczeń można stwierdzić, że filar w piwnicy ma odpowiednią nośność.

2. OBLICZENIE FILARA W ŚCIANIE WEWNĘTRZNEJ

Przyjęto:

• Ciężar własny muru:
  ,

• Wytrzymałość charakterystyczna muru na ściskanie :
  ,

• Współczynnik bezpieczeństwa dla kategorii A wykonania robót na budowie
  ,

• Wymiary filara:
  ,

• Szerokość pasma, z którego przekazywane jest obciążenie na filar na wszystkich kondygnacjach:
  ,

• Grubość muru:
  ,

• Szerokość wieńca:
  ,

• Wysokość ściany w świetle stropów:
  ,

• Rozpiętość stropu w świetle ścian:
  .

Zestawienie obciążeń:

- obciążenie od stropów:
. Powierzchnie obciążenia stropami nad piwnicą i parterem są sobie równe i wynoszą:
,

Do obliczeń przyjęto na poddaszu obciążenie użytkowe jak dla kondygnacji mieszkalnych.

- reakcje ze stropów wynoszą:

od stropu nad parterem:

,

od stropu nad piwnicą:

,

- ciężar ścian:

• ciężar własny muru wynosi :
  ,

• ciężar tynku cem. -wap. (dwustronnego) wynosi:
  

• ciężar własny ściany wynosi:
  

Powierzchnia obciążająca mur:

Siły skupione od ciężaru ścian:

Łączne obciążenie przypadające na wieniec nad filarem w piwnicy, bez redukcji obciążenia użytkowego wynosi:

Obciążenie całkowite w piwnicy:

Określenie smukłości filara

Do określenia smukłości filara przyjęto:

stropy żelbetowe, konstrukcja usztywniona przestrzennie w sposób eliminujący przesuw poziom, rozstaw ścian usztywniających ścianę z filarem

Zatem z warunku
, wynika, że w ścianach występuje usztywnienie u góry i u dołu oraz usztywnienie wzdłuż obu krawędzi pionowych.
Stąd:

Wysokość efektywna ściany wynosi:

Smukłość ściany spełnia zatem warunek:

Określenie wytrzymałości muru

Dla pustaka klasy 20 oraz zaprawy klasy M10 -

Pole przekroju elementu konstrukcji murowej wynosi:

Zatem

Wytrzymałość obliczeniowa muru wynosi:

Sprawdzanie stanu granicznego nośności filara

Do obliczeń przyjęto model przegubowy ze względu na brak odpowiedniego zbrojenia górnego
w węzłach-złączach służących do przeniesienia momentów podporowych. Miejsce przyłożenia sił
w modelu przegubowym pokazano na rysunku:

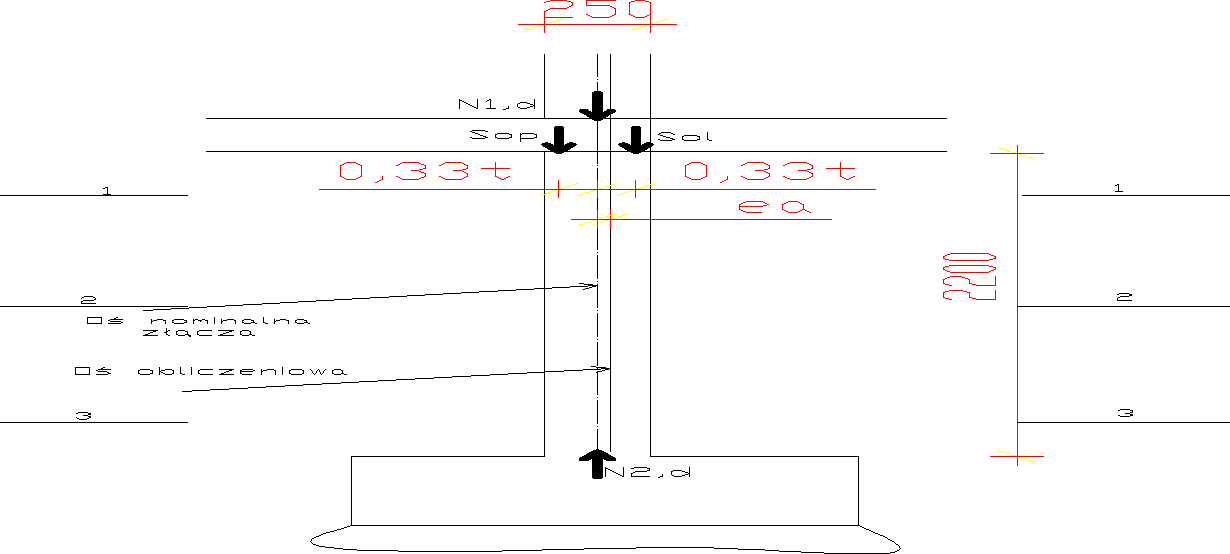
Mimośród przypadkowy:

W przekrojach 1-1 i 2-2 momenty wynoszą:

W przekrojach 1-1, 2-2 mimośrody wynoszą:

Przyjęto do dalszych obliczeń

W przekrojach 1-1 i 2-2 współczynniki redukcyjne
wynoszą:

W przekrojach 1-1 i 2-2 nośności ściany wynoszą:

Stan graniczny nośności w przekrojach 1-1 i 2-2 nie jest przekroczony.

W przekroju 3-3 mimośród wynosi:

Cecha sprężystości muru wykonanego z bloków BSD 250 wynosi:
, a cecha sprężystości dla tego muru pod obciążeniem długotrwałym wynosi:
.

W przekroju 3-3 dla:

Zatem z tabeli:

W przekroju 3-3 nośność ściany wynosi:

Na podstawie przeprowadzonych obliczeń można stwierdzić, że filar w piwnicy ma odpowiednią nośność.

Ławy fundamentowe

OBLICZENIE ŁAWY FUNDAMENTOWEJ POD ŚCIANĄ ZEWNĘTRZNĄ I WEWNĘTRZNĄ

Zaprojektować lawy fundamentowe betonowe pod ścianami konstrukcyjnymi - zewnętrznymi i wewnętrznymi. Przyjęto, że ławy zostaną wykonane z betonu klasy B20, o wytrzymałości

,
.

Ława fundamentowa pod ścianą zewnętrzną:

Zebranie obciążeń:

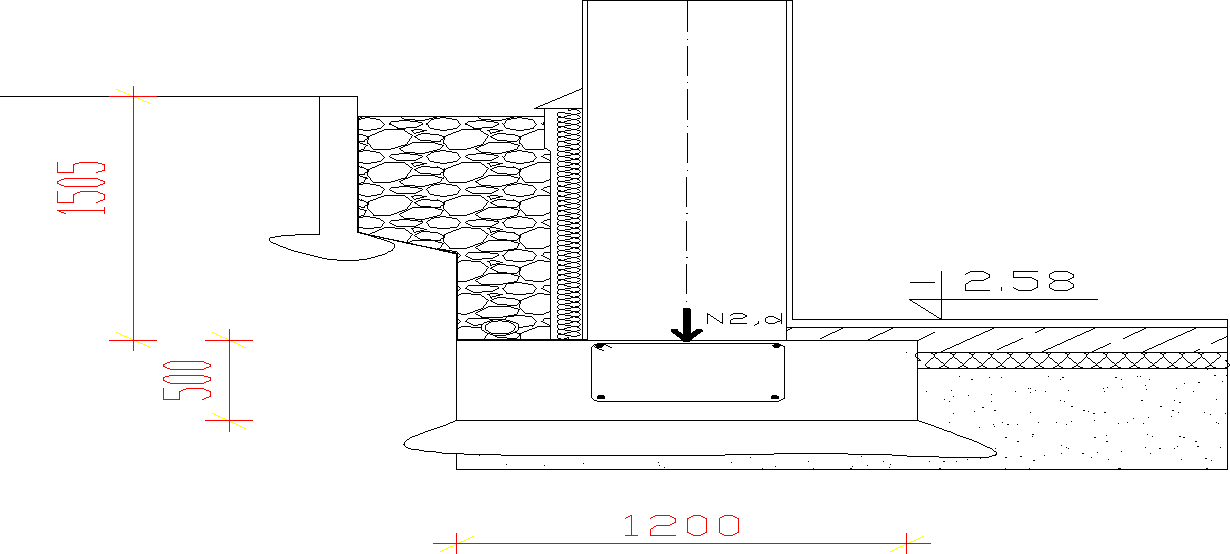
Obliczenie

OBCIĄŻENIA:

MOMENTY:

Minimalna grubość ławy fundamentowej wynosi 11,3 cm, przyjęta grubość ławy w projekcie wynosi 50 cm, zatem zaprojektowana ława ma wymiary wystarczające.

Ława fundamentowa pod ścianą wewnętrzną:

Zebranie obciążeń:

Obliczenie

OBCIĄŻENIA:

MOMENTY:

Minimalna grubość ławy fundamentowej wynosi 12,1 cm, przyjęta grubość ławy w projekcie wynosi 50 cm, zatem zaprojektowana ława ma wymiary wystarczające.

15

---