Oznaczenia

R(t) − funkcja niezawodności,

F(t) − funkcja zawodności,

ET − oczekiwany czas zdatności,

r(t) − pozostały oczekiwany czas zdatności,

f(t) − gęstość prawdopodobieństwa uszkodzenia,

λ(t) − intensywność uszkodzeń,

μ − intensywność odnowy.

Wzory ogólne

,
,

Rozkład wykładniczy czasu zdatności elementu

λ − intensywność uszkodzeń elementu

Dla elementu:
,
,
,

− dla rozkładu wykładniczego intensywność uszkodzeń elementu jest stała

− oczekiwany czas zdatności elementu,

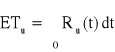
− oczekiwany czas zdatności urządzenia,

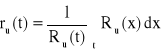
− pozostały oczekiwany czas zdatności urządzenia,

Rozkład jednostajny czasu zdatności elementu

k − kres górny czasu zdatności elementu

Dla elementu:
,

−

,

− oczekiwany czas zdatności elementu,

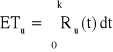
− oczekiwany czas zdatności urządzenia,

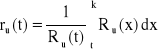
− pozostały oczekiwany czas zdatności urządzenia,

Struktury niezawodnościowe

− szeregowa

Funkcja niezawodności takiej struktury jest iloczynem funkcji niezawodności poszczególnych elementów:

Intensywność uszkodzeń takiej struktury jest równa sumie intensywności uszkodzeń poszczególnych elementów:

− równoległa

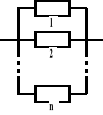
Funkcja zawodności takiej struktury jest iloczynem funkcji zawodności poszczególnych elementów:

Rezerwa nieobciążona

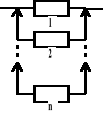
Oczekiwany czas zdatności takiego układu jest równy sumie oczekiwanych czasów zdatności poszczególnych elementów:

Rezerwa obciążona (zwykłe równoległe połączenie)

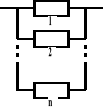
Tu oczekiwany czas zdatności urządzenia liczymy wg wzoru całkowego. Pozostałe parametry [f_u(t), λ_u(t)] liczymy z podstawowych wzorów.

Używane w zadaniach całki i pochodne

,
,
,

Zadanie 1

Urządzenia składa się z dwóch elementów. Uszkodzenie jednego z elementów powoduje uszkodzenie urządzenia. Intensywności uszkodzeń elementów nie zależą od czasu, a ich wartości nie są znane. Intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest znany, a jego wartość jest równa 66 [h] 40 [min]. Obliczyć oczekiwane czasy zdatności elementów.

λ_u = λ₁ + λ₂, λ₁ = 2λ₂ → λ_u = 3λ₂

→
→
→
,

λ₁ = 2λ₂ →
,

Odp. ET₁ = 100 [h], ET₂ = 200 [h].

Zadanie 2

Urządzenia składa się z trzech elementów. Uszkodzenie jednego z elementów powoduje uszkodzenie urządzenia. Intensywności uszkodzeń elementów nie zależą od czasu. Intensywność uszkodzeń drugiego elementu jest trzy razy większa od intensywności uszkodzeń elementu pierwszego, a intensywność uszkodzeń elementu trzeciego jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest równy 10 [h]. Obliczyć oczekiwane czasy zdatności elementów.

λ_u = λ₁ + λ₂ + λ₃, λ₂ = 3λ₁, λ₃ = 2λ₂ → λ₃ = 6λ₁ → λ_u = λ₁ + 3λ₁ + 6λ₁ = 10λ₁

→
→
→
,

λ₂ = 3λ₁ →
,

λ₃ = 6λ₁ →
,

Odp. ET₁ = 100 [h], ET₂ = 33 [h] 20 [min.], ET₃ = 16 [h] 40 [min.].

Zadanie 3

Urządzenie o strukturze szeregowej składa się z jednakowych elementów, których intensywności uszkodzeń nie zależą od czasu. Z ilu elementów składa się to urządzenie, jeżeli oczekiwany czas zdatności elementu jest równy 500 [h], a intensywność uszkodzeń urządzenia jest równa 0,02 [1/h].

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ_u = 0,02 [1/h], ET_e = 500 [h]

Szukane: n = ? (ilość elementów, z których składa się dana struktura niezawodnościowa)

λ_u = λ_e + λ_e + … + λ_e = n⋅λ_e

→
→
→ n = λ_u⋅ET_e = 10

Odp. Urządzenie składa się z 10 elementów.

Zadanie 6

O ile różnią się oczekiwane czasy zdatności dwóch urządzeń zbudowanych z dwóch jednakowych elementów. Pierwsze ma równoległą, a drugie szeregową strukturę. Czas zdatności elementu ma rozkład wykładniczy. Oczekiwany czas zdatności elementu jest równy 120 [h].

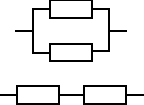
Dla struktury równoległej: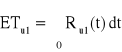
, R_u1(t) = ?

,
,

→

→
→
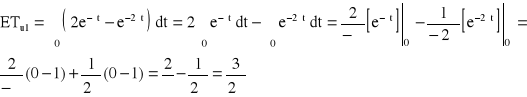
→ ET_u1 = 180 [h]

Dla struktury szeregowej:
, λ_u2 = λ + λ = 2λ →

→ ET_u2 = 60 [h], czyli ET_u1 = 3ET_u2

Odp. Oczekiwany czas zdatności dla struktury równoległej jest 3 razy większy.

Zadanie 7

O ile różnią się oczekiwane czasy zdatności dwóch urządzeń zbudowanych z dwóch jednakowych elementów. Pierwsze ma równoległą, a drugie szeregową strukturę. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 120 [h].

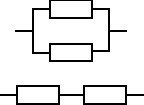
Dla struktury równoległej: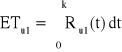
, R_u1(t) = ?

,
,
→
→

→
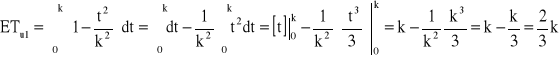
→ k = 240 [h] → ET_u1 = 160 [h]

Dla struktury szeregowej: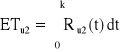
, R_u2(t) = ?

,
→

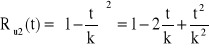
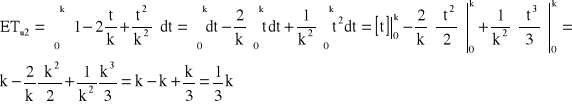
k = 240 [h] → ET_u2 = 80 [h], czyli ET_u1 = 2ET_u2

Odp. Oczekiwany czas zdatności dla struktury równoległej jest 2 razy większy.

Zadanie 8

Urządzenie o strukturze równoległej składa się z dwóch jednakowych elementów. Który rozkład czasu zdatności, jednostajny czy wykładniczy, będzie korzystniejszy z punktu widzenia niezawodności rozpatrywanego urządzenia. Oczekiwany czas zdatności elementu jest równy 60 [h].

Dla rozkładu jednostajnego: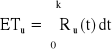
, R_u(t) = ?

,
,
→
→

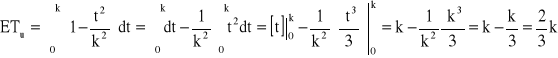
, k = ?

→
→ k = 120 [h] → ET_u = 80 [h]

Dla rozkładu wykładniczego: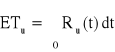
, R_u (t) = ?

,
,

→

,
→
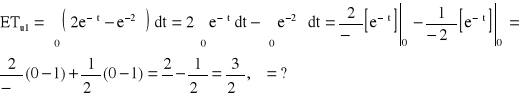
→ ET_u = 90 [h]

Jak powyżej wykazano oczekiwany czas zdatności dla rozkładu wykładniczego jest większy, wobec tego ten rozkład czasu zdatności jest korzystniejszy z punktu widzenia niezawodności urządzenia.

Zadanie 9

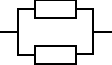
Urządzenia o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 100 [h]. Obliczyć intensywność uszkodzeń tego urządzenia.

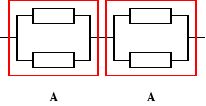
λ_u(t) = λ_A(t) + λ_A(t) = 2λ_A(t),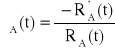
, R_A(t) = ?

,
,
→

,
,
→

→
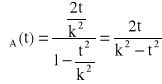
→ k = 200 [h] →

Odp.
.

Zadanie 10

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym zero. Obliczyć stosunek oczekiwanego czasu zdatności elementu do oczekiwanego czasu zdatności urządzenia.

,
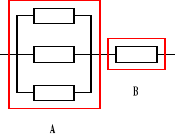
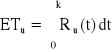
, R_u(t) = ?

,
,

,
,
→
→

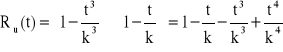
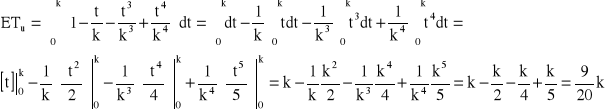
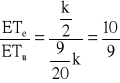
Odp.
.

Zadanie 11

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym zero. Oczekiwany czas zdatności urządzenia jest równy 700 [h]. Obliczyć oczekiwany czas zdatności elementu.

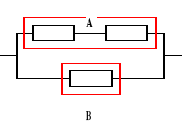
, k = ?

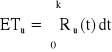
, R_u(t) = ?

,

,
,
,

,
→

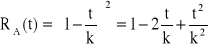
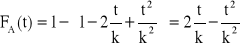
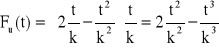
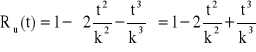
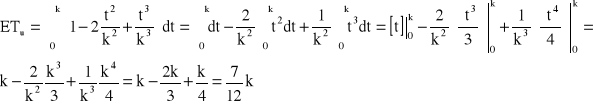
→ k = 1200 [h] → ET_e = 600 [h]

Odp. ET_e = 600 [h].

Zadanie 12

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z trzech elementów, których intensywności uszkodzeń nie zależą od czasu, a ich wartości nie są znane. Intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest równy 700 [h]. Obliczyć oczekiwane czasy zdatności elementów 1 i 2.

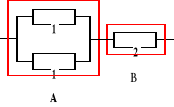
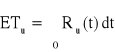
, R_u(t) = ?

,

,
,

→

, λ₁ = 2λ₂ →

→
,
,
,

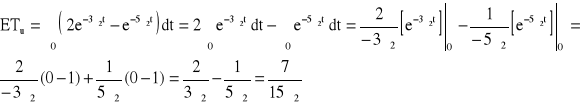
Odp. ET₁ = 750 [h], ET₂ = 1500 [h].

Zadanie 16

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 120 [h]. Obliczyć oczekiwany czas zdatności urządzenia.

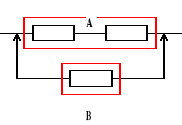
ET_u = ET_A + ET_B,
,
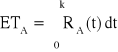
, R_A(t) = ?

,
,

→
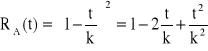
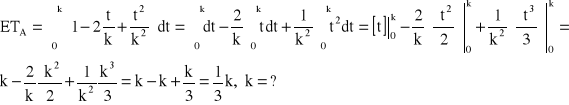
→ k = 240 [h] → ET_A = 80 [h] → ET_u = 200 [h]

Odp. ET_u = 200 [h].

Zadanie 17

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Oczekiwany czas zdatności elementu jest równy 120 [h]. Obliczyć oczekiwany czas zdatności urządzenia, jeżeli intensywność uszkodzeń elementu jest stała.

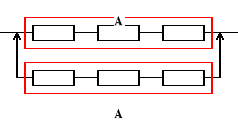
ET_u = ET_A + ET_A = 2ET_A, ET_A = ?

, λ_A = λ + λ + λ = 3λ →
, λ = ?

→
→ ET_A = 40 [h] → ET_u = 2ET_A = 80 [h]

Odp. ET_u = 80 [h].

Zadanie 21

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech elementów, których intensywności uszkodzeń nie zależą od czasu, a ich wartości nie są znane. Oczekiwany czas zdatności urządzenia jest równy 500 [h]. Obliczyć oczekiwane czasy zdatności elementów wiedząc, że intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego.

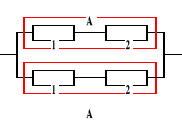
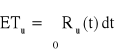
, R_u(t) = ?

,

,
,
,

λ₁ = 2λ₂ →
→

,

→
,
,
,

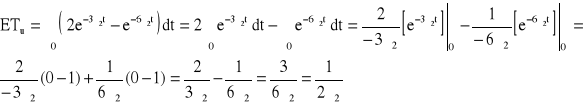
Odp. ET₁ = 500 [h], ET₂ = 1000 [h].

Zadanie 22

Czas zdatności pewnego obiektu ma rozkład jednostajny o kresie dolnym równym 0, a kres górny nie jest znany. Wiadomo, że oczekiwany czas zdatności obiektu jest równy 5 lat. Obliczyć prawdopodobieństwo tego, że rozpatrywany obiekt:

a) uszkodzi się w czwartym roku użytkowania,

b) bezawaryjnie przepracował trzy lata, uszkodzi się w czwartym roku pracy.

→
→ k = 10 lat − kres górny czasu zdatności obiektu

T − zmienna losowa czasu pracy obiektu do chwili powstania uszkodzenia

a)
,
,

,
→

b)
,

,
(policzone w punkcie a)

.

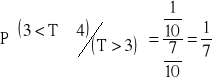
Odp.
,

Zadania z ćwiczeń

Zadanie 25

Czas zdatności obiektu ma rozkład jednostajny , którego kres dolny jest równy zero, kres górny jest równy 10 lat. Obliczyć prawdopodobieństwo tego, że rozpatrywany obiekt:

a) uszkodzi się w trzecim lub czwartym roku użytkowania,

b) uszkodzi się w dziesiątym roku użytkowania, jeśli wiadomo, że bezawaryjnie przepracował dziewięć lat.

= 10 lat − kres górny czasu zdatności obiektu

T − zmienna losowa czasu pracy obiektu do chwili powstania uszkodzenia

a)
,
,

,
→

b)
,

,
,
→

.

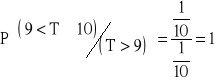
Zadanie 26

Czas zdatności obiektu ma rozkład wykładniczy z parametrem λ. Wiadomo, że obiekt przepracował bezawaryjnie s jednostek czasu. Obliczyć prawdopodobieństwo tego, że nie przepracuje następnych x jednostek czasu.

T − zmienna losowa czasu pracy obiektu do chwili powstania uszkodzenia

,
,
,

,
,

.

Zadanie 27

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czasy zdatności elementów mają rozkłady wykładnicze o znanym parametrze λ. Obliczyć oczekiwany czas zdatności rozpatrywanego urządzenia.

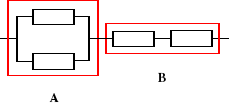
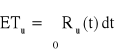
, R_u(t) = ?

, R_A(t) = ?, R_B(t) = ?

,
,

→

,
→

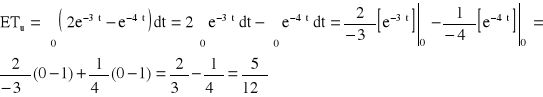
Odp.
.

Zadanie 28

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z elementów, których czasy zdatności mają rozkłady wykładnicze o znanych parametrach wynoszących odpowiednio λ₁, λ₂, λ₃. Obliczyć intensywność uszkodzeń rozpatrywanego urządzenia.

,
,
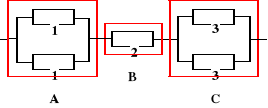
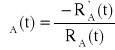
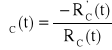
, R_A(t) = ?, R_C(t) = ?

,
,

→

,

→

Odp.
.

Zadanie 29

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z 4 jednakowych elementów. Czasy zdatności elementów mają rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności urządzenia jest równy 800 [h]. Obliczyć gęstość prawdopodobieństwa uszkodzenia elementu rozpatrywanego urządzenia.

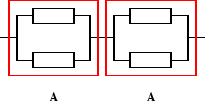
, k = ?

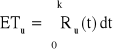
, R_u(t) = ?

, R_A(t) = ?

,
,
→

→

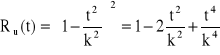
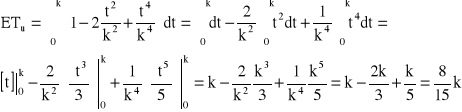
→ k = 1500 [h] →

Odp.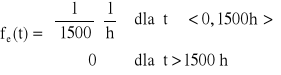
.

Zadanie 30

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z elementów, których czasy zdatności mają rozkłady wykładnicze o znanych parametrach odpowiednio równych λ₁ i λ₂. Obliczyć oczekiwany czas zdatności oraz intensywność uszkodzeń rozpatrywanego urządzenia.

,
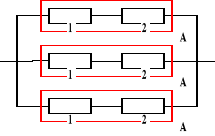
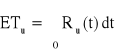
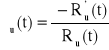
, R_u(t) = ?

,
,
,

,
,
,

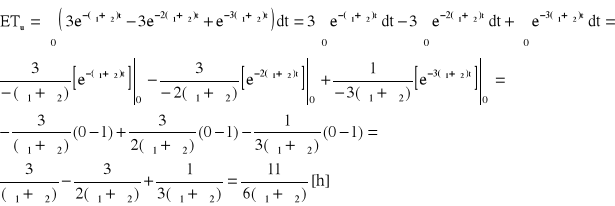
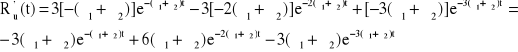
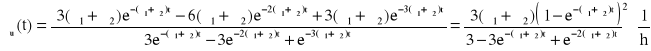
Odp.
,
.

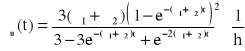
Zadanie 31

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z 4 jednakowych elementów. Czasy zdatności elementów mają rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest znany i równy 300 [h]. Obliczyć oczekiwany czas zdatności oraz intensywność uszkodzeń rozpatrywanego urządzenia dla czasu równego oczekiwanego czasowi zdatności elementu.

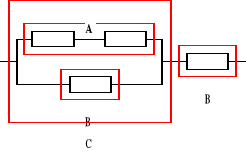
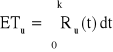
, R_u(t) = ?

,
,

,
,
,

,
,

,

→
→
→

,
→

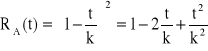
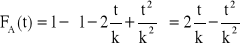
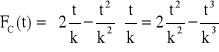
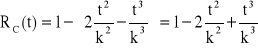
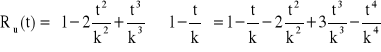
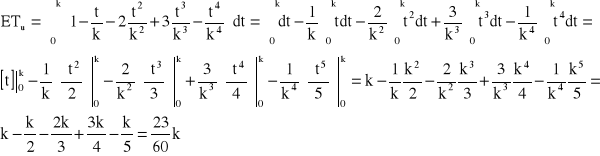
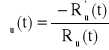
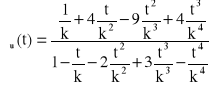
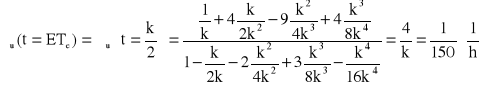
Odp.
,
.

Zadanie 33

Czas zdatności obiektu ma rozkład jednostajny, którego kres dolny jest równy 0. Obiekt bezawaryjnie przepracował 1200 [h]. Oczekiwany pozostały czas zdatności tego obiektu jest równy 400 [h]. Obliczyć gęstość prawdopodobieństwa uszkodzeń rozpatrywanego obiektu.

, k = ?

,
,

→
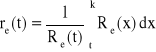
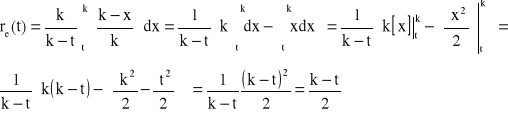
→ k = 2000 [h] →

Odp.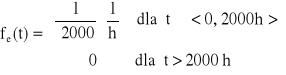
.

Zadanie 34

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z dwóch jednakowych elementów. Czas zdatności elementu ma rozkład wykładniczy o znanym parametrze λ. Wyznaczyć oczekiwany pozostały czas zdatności [r_u(t)] tego urządzenia oraz obliczyć granicę, do jakiej dąży jego wartość, gdy czas dąży do nieskończoności.

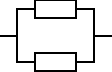
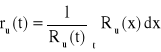
, R_u(t) = ?

,
,
→

,

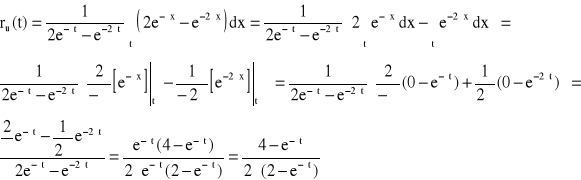
Odp.
,
.

Zadanie 35

Urządzenie o strukturze szeregowej składa się z dwóch jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0 i kresie górnym równym k. Obliczyć pozostały oczekiwany czas zdatności tego urządzenia.

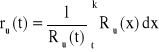
, R_u(t) = ?

,
→
,

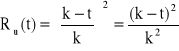
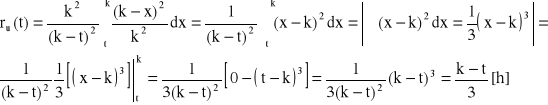
Odp.
dla t ∈ (0, k >.

dla rozkładu jednostajnego gęstość prawdopodobieństwa uszkodzenia elementu jest stała

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 66 [h] 40 [min.]

Szukane: ET₁ = ?, ET₂ = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₂ = 3λ₁, λ₃ = 2λ₂, ET_u = 10 [h]

Szukane: ET₁ = ?, ET₂ = ?, ET₃ = ?

Rozkład czasu zdatności elementu − wykładniczy z parametrem λ

Dane: ET_e = 120 [h]

Porównać oczekiwane czasy zdatności obu struktur

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Porównać oczekiwane czasy zdatności obu struktur

Dane: ET_e = 60 [h]

Porównać oczekiwane czasy zdatności urządzenia dla rozkładu jednostajnego i wykładniczego

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 100 [h]

Szukane: λ_u(t) = ?

Rozkład czasu zdatności elementu − jednostajny

Szukane:

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_u = 700 [h]

Szukane: ET_e = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 700 [h]

Szukane: ET₁ = ?, ET₂ = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu −

wykładniczy

Dane: ET_e = 120 [h]

Szukane: ET_u = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 500 [h]

Szukane: ET₁ = ?, ET₂ = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ

Szukane: ET_u = ?

Rozkład czasu zdatności elementu −

wykładniczy

Dane: λ₁, λ₂, λ₃

Szukane: λ_u(t) = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_u = 800 [h]

Szukane: f_e(t) = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁, λ₂

Szukane: ET_u = ?, λ_u(t) = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 300 h

Szukane: ET_u = ?, λ_u(t = ET_e) = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ

Szukane:
,

Rozkład czasu zdatności elementu − jednostajny

Szukane:

---