Zadanie 4

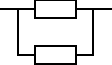
Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego będącego rezerwą obciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy
120 [h]. Wyznaczyć przedział czasu, w którym gęstość prawdopodobieństwa uszkodzeń urządzenia jest większa od gęstości prawdopodobieństwa uszkodzeń elementu.

,
, k = ?, R_u(t) = ?

→
→ k = 240 [h]

,
,
→

,
→

→
→

Odp. t ∈ (120h, 240h>

Zadanie 5

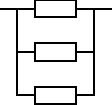
Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą obciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 100 [h]. Wyznaczyć gęstość prawdopodobieństwa uszkodzeń tego urządzenia.

, R_u(t) = ?

,
,
→

→
→

→
→ k = 200 [h] →

Odp.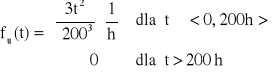

Zadanie 13

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Gęstość prawdopodobieństwa uszkodzeń elementu jest równa 0,001 [1/h]. Wyznaczyć oczekiwany czas zdatności urządzenia.

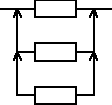
ET_u = ET_e + ET_e + ET_e = 3ET_e, ET_e = ?

→
, k = ?,
→
→ k = 1000 [h] →

Odp. ET_u = 1500 [h].

Zadanie 14

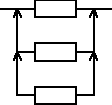
Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności urządzenia jest równy 1500 [h]. Wyznaczyć gęstość prawdopodobieństwa uszkodzeń elementu.

, k = ?

ET_u = ET_e + ET_e + ET_e = 3ET_e,
→

→ k = 1000 [h] →

Odp.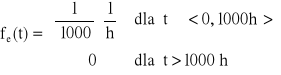
.

Zadanie 15

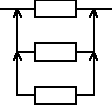
Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład wykładniczy z parametrem λ równym 0,005 [1/h]. Wyznaczyć oczekiwany czas zdatności urządzenia.

ET_u = ET_e + ET_e + ET_e = 3ET_e, ET_e = ?

→

Odp. ET_u = 600 [h].

Zadanie 16

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 120 [h]. Obliczyć oczekiwany czas zdatności urządzenia.

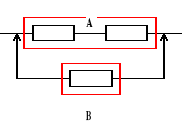
ET_u = ET_A + ET_B,
,
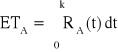
, R_A(t) = ?

,
,

→
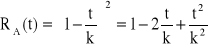
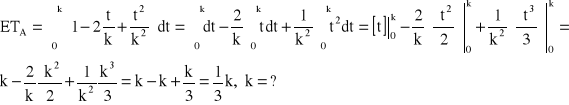
→ k = 240 [h] → ET_A = 80 [h] → ET_u = 200 [h]

Odp. ET_u = 200 [h].

Zadanie 17

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Oczekiwany czas zdatności elementu jest równy 120 [h]. Obliczyć oczekiwany czas zdatności urządzenia, jeżeli intensywność uszkodzeń elementu jest stała.

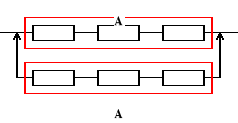
ET_u = ET_A + ET_A = 2ET_A, ET_A = ?

, λ_A = λ + λ + λ = 3λ →
, λ = ?

→
→ ET_A = 40 [h] → ET_u = 2ET_A = 80 [h]

Odp. ET_u = 80 [h].

Zadanie 18

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Gęstość prawdopodobieństwa uszkodzenia elementu jest równa 1/300 [1/h]. Obliczyć oczekiwany czas zdatności urządzenia.

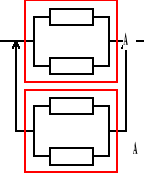
ET_u = ET_A + ET_A = 2ET_A, ET_A = ?,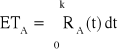
, R_A(t) = ?

,
,
→
→

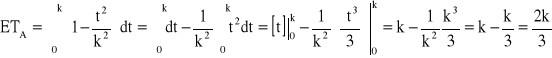
, k = ?,
→
→ k = 300 [h] →

Odp. ET_u = 400 [h].

Zadanie 19

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Oczekiwany czas zdatności urządzenia jest równy 450 [h]. Obliczyć oczekiwany czas zdatności elementu, jeżeli intensywność uszkodzeń elementu jest stała.

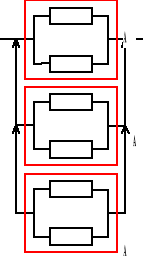
ET_u = ET_A + ET_A + ET_A = 3ET_A, ET_A = ?,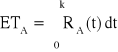
, R_A(t) = ?

,
,

→

,
→
→

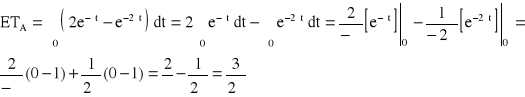
Odp.
.

Zadanie 20

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład wykładniczy o wartości oczekiwanej 1/λ. Wyznaczyć gęstość prawdopodobieństwa uszkodzenia rozpatrywanego urządzenia.

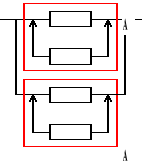
, R_u(t) = ?

,

Skorzystamy w tym momencie z wyniku zadania 36, w którym wyliczono funkcję zawodności [F_A(t)] struktury A (rezerwa nieobciążona):

→
→

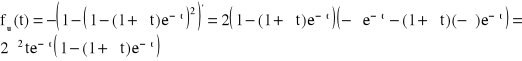
Odp.

Zadanie 23

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego będącego rezerwą obciążoną. Intensywności elementów są stałe i równe 0,01 [1/h]. Intensywności odnowy również są stałe i równe 0,1 [1/h]. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne. Pomijamy tzw. uszkodzenie o wspólnej przyczynie oraz zakładamy, że nie ma żadnych ograniczeń, co do liczby elementów, które mogą być odnawiane w tym samym czasie.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2, szukamy P₂

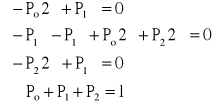
Z drugiego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

Z pierwszego równania:

Z trzeciego równania:
, czyli:
i podstawiamy do ostatniego równania

→
→

Podstawiając dane liczbowe:
,
otrzymujemy:

Odp. Stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadanie 24

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego. Element rezerwowy jest rezerwą obciążoną. Intensywność uszkodzeń elementu jest równa 0,001 [1/h]. Po wystąpieniu uszkodzenia dowolnego elementu urządzenie jest nadal zdatne, ale intensywność uszkodzeń działającego elementu wzrasta o 1,5. Do odnowy uszkodzonych elementów przystępuje się, gdy urządzenie jako całość przechodzi w stan niezdatności. Intensywność odnowy całego urządzenia jest równa 0,1 [1/h]. W trakcie odnowy usuwa się wszystkie uszkodzenia. Uszkodzenia o wspólnej przyczynie pomijamy. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2, szukamy P₂.

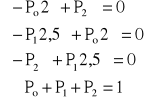
z jednego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

z pierwszego równania:
, z trzeciego równania:

i podstawiamy do ostatniego równania otrzymując:

po przekształceniach otrzymujemy:

podstawiając dane liczbowe:
,
otrzymujemy:
.

Odp. Stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadania z ćwiczeń

Zadanie 36

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład wykładniczy o znanym parametrze λ. Elementy rezerwowe stanowią rezerwę nieobciążoną. Wyznaczyć funkcję niezawodności oraz intensywność uszkodzeń rozpatrywanego urządzenia.

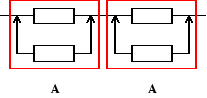
Funkcja zawodności struktury A (rezerwa nieobciążona) urządzenia może być potraktowana jako dystrybuanta sumy niezależnych zmiennych losowych i wyrażona wzorem (indeks „1” jest przypisany dla elementu podstawowego, zaś „2” dla elementu rezerwowego):

,
→
→

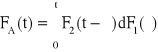
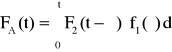
Wzór ten korzystając z oznaczeń na poniższym rysunku można interpretować jak niżej:

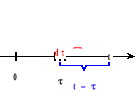
Iloczyn f₁(τ)dτ przedstawia prawdopodobieństwo tego, że element podstawowy uszkodził się w bezpośrednim sąsiedztwie „chwili” τ (w bardzo małym przedziale czasu, którego środkiem jest τ). F₂(t − τ) jest to prawdopodobieństwo tego, że element rezerwowy przepracował mniej niż (t − τ) jednostek czasu. Należy rozpatrzyć wszystkie możliwości tego, że element pierwszy uszkodził się w chwili τ, a element drugi nie przetrwał w stanie zdatności czasu (t − τ), co przedstawia powyższa całka oznaczona obliczana w granicach od 0 do t.

Elementy są jednakowe, zatem funkcja zawodności i gęstość prawdopodobieństwa uszkodzeń każdego z nich są odpowiednio równe:

Funkcja zawodności struktury A urządzenia zatem jest równa:

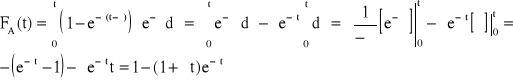
Funkcja niezawodności struktury A może być obliczona ze wzoru:

→

Intensywność uszkodzeń urządzenia obliczamy ze wzoru:

λ_u(t) = λ_A(t) + λ_A(t) = 2λ_A(t),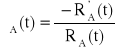

→
→

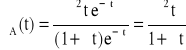
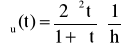
Odp.
,
.

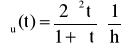
Zadanie 37

Urządzenie o szeregowej strukturze niezawodnościowej składa się z pięciu jednakowych elementów. Intensywność uszkodzeń elementu jest równa λ, a intensywność odnowy jest równa μ. Obliczyć stacjonarny współczynnik gotowości tego urządzenia, zakładając, że element może ulec zniszczeniu wtedy, gdy urządzenie działa oraz, że nie rozpatrujemy tzw. uszkodzenia o wspólnej przyczynie.

Rozpatrywane stany urządzenia:

0 - urządzenie zdatne,

1 - urządzenie niezdatne

P_o, P₁ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1

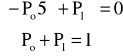
Współczynnik gotowości − k_g = P_o

,
→

Odp.
.

Zadanie 38

Urządzenie o szeregowej strukturze niezawodnościowej składa się z trzech jednakowych elementów. Intensywność uszkodzeń elementu jest równa λ, a intensywność odnowy jest równa μ. W przypadku wystąpienia uszkodzenia o wspólnej przyczynie uszkodzenie urządzenia następuje z intensywnością λ_w. Odnowienie tak uszkodzonego urządzenia następuje z intensywnością odnowy μ_w. Obliczyć stacjonarny współczynnik gotowości tego urządzenia.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne,

1 - jeden element niezdatny,

3 - trzy elementy niezdatne

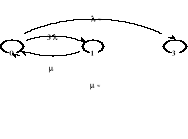
P_o, P₁, P₃ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 3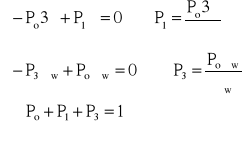

Współczynnik gotowości − k_g = P_o

→

Odp.

Zadanie 39

Urządzenie o równoległej strukturze niezawodnościowej składa się z dwóch jednakowych elementów. Intensywność uszkodzeń elementu jest równa λ. Intensywność odnowy elementu może przyjmować jedną z dwóch wartości. Jest ona równa μ₁, gdy odnawiany jest jeden element. Jeśli w tym samym czasie „równolegle” są poddawane odnowie obydwa elementy intensywność odnowy elementu spada, przyjmując wartość μ₂. W rozpatrywanym przypadku nie ma żadnych ograniczeń, co do liczby elementów, które mogą być odnawiane w tym samym czasie. Wyznaczyć stacjonarny współczynnik gotowości tego urządzenia, pomijając tzw. uszkodzenie o wspólnej przyczynie.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne,

1 - jeden element niezdatny,

2 - dwa elementy niezdatne

Ponieważ nie uwzględniamy uszkodzeń o wspólnej przyczynie, przejścia oznaczonego linią przerywaną nie bierzemy dalej pod uwagę.

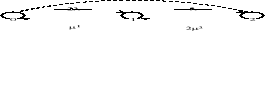
P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

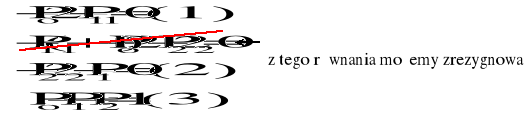
Ostatnie równanie tworzymy korzystając z warunku normującego.

Urządzenie ma strukturę równoległą, gdy co najmniej jeden element jest zdatny to urządzenie jest zdatne. Prawdopodobieństwo stacjonarne takiej sytuacji jest tzw. stacjonarnym współczynnikiem gotowości − k_g, co można zapisać jak niżej:

, czyli należy wyznaczyć P₂.

z równania (1) wyznaczamy P_o:

z równania (2) wyznaczamy P₁:
, i podstawiając do równania (1):

podstawiamy wyliczone wartości P_o i P₁ do równania (3):

→

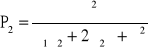
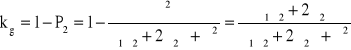
Odp.
.

Zadanie 40

Urządzenie składa się z elementu podstawowego i jednego elementu rezerwowego. Element rezerwowy jest rezerwą nieobciążoną. Intensywność uszkodzeń elementu jest równa λ, zaś intensywność odnowy jest równa μ. Jeżeli przed zakończeniem odnowy uszkodzeniu ulegnie również drugi element, to urządzenie ulegnie zniszczeniu − nie można go odnowić. Pomijając uszkodzenie o wspólnej przyczynie, obliczyć stacjonarny współczynnik gotowości tego urządzenia.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

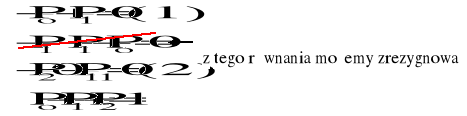
z równania (2) P₁ = 0, czyli z równania (1) P_o = 0, stąd P₂ = 1 i k_g = 0.

Zadanie 41 (zadanie ze skryptu mgra inż. T. Rutkowskiego)

Urządzenie składa się z elementu podstawowego i jednego elementu rezerwowego. Intensywność uszkodzeń elementu jest równa λ₁, w gdy element pracuje i λ₂ gdy jest w rezerwie. Uszkodzone elementy są odnawiane kolejno, a intensywność odnowy elementu jest równa μ. Pomijając uszkodzenie o wspólnej przyczynie obliczyć stacjonarny współczynnik gotowości tego urządzenia, gdy element rezerwowy będzie rezerwą:

a) częściowo obciążoną

b) obciążoną

c) nieobciążoną

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

a)

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

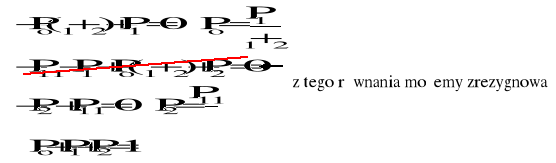
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

→

→

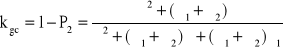
b) w tym przypadku λ₂ = λ₁

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

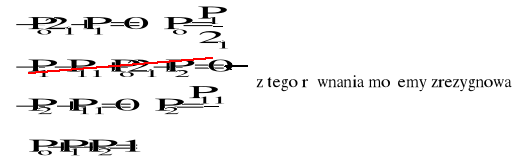
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

→
,

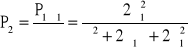
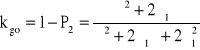
c) w tym przypadku λ₂ = 0

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

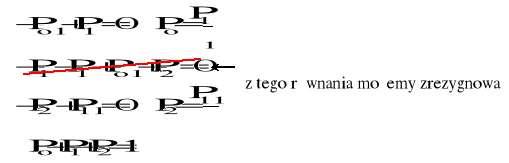
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

,
→
.

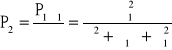
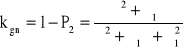
Rezerwa nieobciążona

Rozkład czasu zdatności elementu − wykładniczy z parametrem λ

Dane: λ = 0,005 [1/h]

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_u = 1500 [h]

Szukane: f_e(t) = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane:

Szukane: ET_u = ?

Rezerwa obciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 100 [h]

Szukane: f_u(t) = ?

Rezerwa obciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Szukane: przedział czasu, dla którego f_u(t) > f_e(t)

Rezerwa nieobciążona

Rozkład czasu zdatności − jednostajny

Dane:

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności − wykładniczy

Dane: ET_u = 450 [h]

Szukane: ET_e = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ

Szukane: R_u(t) = ?, λ_u(t) = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu −

wykładniczy

Dane: ET_e = 120 [h]

Szukane: ET_u = ?

Układ mieszany: rezerwa nieobciążona i obciążona

Rozkład czasu zdatności − wykładniczy

Dane:

Szukane: f_u(t) = ?

---