WIELKOŚCI FIZYCZNE

Wielkości mechaniczne (układ jednostek SI)

Jednostki podstawowe:

długość - metr [m], masa - kilogram [kg], czas - sekunda [s]

jednostki uzupełniające:

kąt płaski - radian [rad], kąt bryłowy - steradian [sr]

Działania na wielkościach; zgodność jednostek

Wielkości złożone:

wielkość W = funkcja (zbiór wielkości: w₁, w₂ ...)

Wielkości skalarne i wektorowe w fizyce

Skalar - wyznaczony przez liczbę (na ogół mianowaną )

Wektor - wyznaczony przez:

1) wartość liczbową (na ogół mianowaną)

2) kierunek (prosta)

3) zwrot (początek - koniec)

W pewnych przypadkach istotny jest punkt przyłożenia.

Graficzne przedstawienie wektora

Oznaczenie wektora -
lub w (w druku) albo
. A - początek, B - koniec wektora

Grot strzałki oznacza zwrot od A do B.

Wartość wektora
- długość odcinka AB (w odpow. skali), oznaczana najczęściej przez w (kursywa, bez strzałki nad literą), czasami przez |w| albo |
|.

Wektor przeciwny do wektora
: oznaczenie -
wartość i kierunek takie jak wektor
, ale zwrot przeciwny, tzn. zamiana miejsc początku i grota (odwrócenie strzałki o 180^o)

Działania na wektorach

1) Mnożenie wektora
przez liczbę a :
= a

wartość w_m = |a|w, kierunek
taki jak kierunek
, zwrot
zgodny ze zwrotem
dla a > 0,

zwrot
przeciwny do zwrotu
dla a < 0.

2) Dodawanie (składanie) wektorów
i

=
+

lub

reguła równoległoboku

jest przekątną równoległoboku

zbudowanego na wektorach
i

- suma wektorów
i
;
i
- składowe sumy

W fizyce i technice wektor
nazywany jest wektorem wypadkowym lub krótko wypadkową wektorów
i
.

3) Odejmowanie wektorów
i

=
-
=
+ (-
)

jest drugą przekątną równoległoboku

zbudowanego na wektorach
i

4) Iloczyn skalarny wektorów
i
:

•
= w₁·w₂·cos∡(
,
)

Podstawowe własności działań :

a (
+
) = a
+ a

+
=
+
(przemienność dodawania wektorów)

(
+
) +
=
+ (
+
) =
+
+
(łączność)

-
= - (
-
)

•
=
•
(przemienność mnożenia skalarnego)

• (
+
) =
•
+
•

Opis wektora w układzie współrzędnych

Rzut wektora
na wybrany kierunek (określony przez prostą p)

 - kąt wektora z prostą p

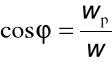
W układzie współrzędnych XYZ rzuty końców wektora
na osie OX, OY i OZ wyznaczają składowe
,
i
tak, że :
.

Wprowadzamy jednostkowe wektory :
,
,
(i, j, k) skierowane wzdłuż osi układu tzw. wersory osi.
=
=
=1.

Analityczna postać wektora :

w_x, w_y, w_z - składowe (współrzędne) algebraiczne wektora

mogą być ujemne, np. w_x < 0, gdy ∡(
,
) > 90°

Z twierdzenia Pitagorasa

,
,

zatem

w_x = w cosα , w_y = w cosβ , w_z = w cosγ

Cosinusy kierunkowe:

,
,
;

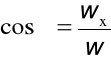
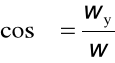
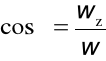
cos²α + cos²β + cos²γ = 1

Wektor
na płaszczyźnie XY

,

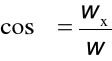
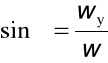
w_x = w cosα, w_y = w sinα,

,

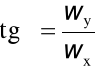
α + β = 90° ⇒ cos²α + cos²β = cos²α + sin²α = 1

Działania na wektorach wykonuje się na składowych np.:

,

Ponieważ
,

więc
,

KINEMATYKA

Opis ruchu punktu materialnego

Wektor wodzący punktu  początek w początku O układu współrzędnych XYZ, koniec (grot) w opisywanym punkcie P :
,
, ⇒ x = x(t), y = y(t), z = z(t)

t = t₂  t₁

Prędkość chwilowa: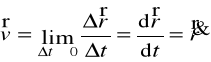

Składowe (współrzędne) prędkości:

,
,
.

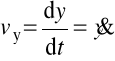
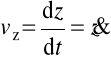
Prędkość chwilowa

jest styczna do kierunku ruchu.

Oznaczamy s  długość łuku drogi PP^' (s = s  s₀)

Wartość prędkości chwilowej (szybkość):

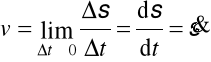
Szybkość średnia v_śr = s/t (zwykle zwana prędkością średnią)

Przyjmując t₁ = 0, t₂ = t i s₀ = 0 mamy v_śr = s / t.

Prędkość jest funkcją czasu, zmienia wartość i (lub) kierunek :

=
(t) ⇒ v_x = v_x(t), v_y = v_y(t), v_z = v_z(t)

Przyspieszenie :

,

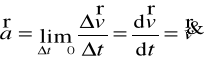
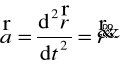
Składowe (współrzędne) przyspieszenia :

,
,

,
,

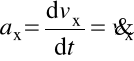
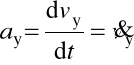
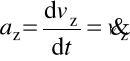
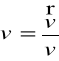
- wersor kierunku prędkości (styczny); |
| = 1

⇒

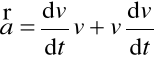
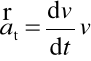
- przyspieszenie styczne
( ozn. też -
,
) wartość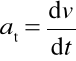
- określa zmianę wartości prędkości,

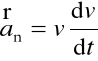
- przyspieszenie normalne (dośrodkowe -
) określa zmianę kierunku prędkości

Całkowite przyspieszenie:

Gdy t₂ → t₁ to φ → 90° .

∡
→ 90°, ∡
→ 90°

,

Składanie ruchów

Ruch skomplikowany może być w pewnych przypadkach traktowany jako złożenie ruchów prostych (składowych). Zasada niezależności ruchów :

na dany ruch prosty nie mają wpływu inne ruchy proste.

Jest to konsekwencja niezależności działania sił.

Rozkładamy ruch złożony tak, aby prosto opisać ruchy składowe.

Przykład : rozkład na dwa ruchy składowe

w tym samym czasie t

stąd prędkość wypadkowa :

- prędkości w ruchach 1. i 2.

wartość prędkości wypadkowej

z twierdzenia cosinusów:

v² = v₁² + v₂² - 2v₁ v₂ cos(180° - α) = = v₁² + v₂² + 2v₁ v₂ cosα

Względność ruchu

- wektor wodzący punktu A , ( względem punktu O )

- wektor wodzący punktu B - // -

- wektor wodzący

punktu B względem punktu A

po upływie czasu Δt następuje

zmiana
o
i zmiana
o

zatem :

stąd prędkość punktu B względem punktu A

v²_BwA = v_A² + v_B² - 2v_A·v_B·cosα

składowe prostopadłe - twierdzenie cosinusów

przechodzi w twierdzenie Pitagorasa

Przykład: przeprawa przez rzekę

szary akwen - woda nieruchoma (stojąca),

niebieski akwen - woda płynąca, przyjmujemy stałą prędkość wody względem brzegów na całej szerokości rzeki

a) z kadłubem „na wprost” (prostopadle do brzegu)

v_o - prędkość wody względem brzegów (v_A)

v_m - prędkość motorówki względem wody (v_AwB)

v_w - prędkość motorówki względem brzegów (wypadkowa v_B)

⇒

……………………………………………………………………………………………………………………………………………..……..

b) uwzględnienie znoszenia przez prąd rzeki

⇒

Ale

Ważne przykłady opisu ruchów

1. Ruch jednostajnie przyspieszony po prostej ; a = a_t = const.

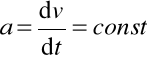
, stąd v = a t + C , gdzie C jest pewną stałą

Żądamy, aby dla pewnej chwili t = t₀ - prędkość v = v₀. Jest to tzw. pierwszy warunek początkowy .

Daje to stałą C = v₀ - at₀ , zatem v = v₀ + a (t - t₀) .

Ale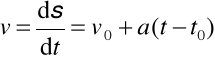
stąd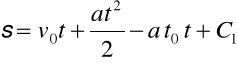
. Nakładamy drugi warunek początkowy: s = s₀ dla t = t₀ . Druga stała wynosi więc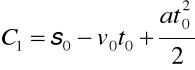
.

Dostajemy wzór na drogę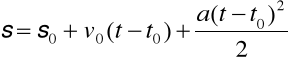
.

Zwykle przyjmujemy t₀ = 0 i s₀ = 0 otrzymując :

v = v₀ + at oraz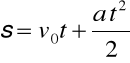

2. Ruch punktu materialnego po okręgu

promień okręgu

r = const

φ - kąt między

a

φ = φ(t)

x = r·cos φ

y = r·sin φ

wektor wodzący punktu P :
= (r·cos φ)
+ (r·sin φ)

współrzędne wektora prędkości :

,

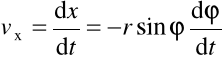
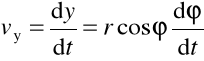
Określamy prędkość kątową: wartość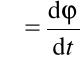

- wektor prostopadły do płaszczyzny okręgu,

Zwrot
wyznaczony jest przez regułę śruby prawoskrętnej.

Zatem składowe prędkości wynoszą:

v_x = - r ω sin φ, v_y = r ω cos φ,

a wartość prędkości: v = ω r , (v =
).

składowe przyspieszenia:

,

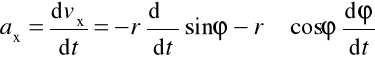
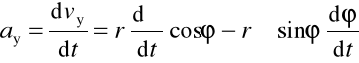
Określamy przyspieszenie kątowe: wartość

- wektor skierowany tak, jak wektor
, przy czym zwrot wektora
jest zgodny ze zwrotem
gdy ω wzrasta, a przeciwny do zwrotu
gdy ω maleje.

Składowe przyspieszenia można więc zapisać w postaci

a_x = - r ε sinφ - r ω² cosφ , a_y = r ε cosφ - r ω² sinφ

Wektor przyspieszenia można napisać następująco

= r ε (-sinφ·
+ cosφ·
) - ω² (r cosφ·
+ r sinφ·
).

Składowa r ε (-sinφ·
+ cosφ·
) ma kierunek i zwrot wektora prędkości
, jest to więc przyspieszenie styczne
.

Zatem przyspieszenie styczne wynosi

= r ε (-sinφ·
+ cosφ·
)

i ma wartość :

a_t = r ε . (a_t = dv/dt = r dω/dt = r ε)

Składowa - ω² (r cosφ·
+ r sinφ·
) ma kierunek promienia
, ale przeciwny do niego zwrot, czyli zwrot do środka okręgu.

Jest to zatem przyspieszenie normalne (dośrodkowe)

=
= - ω² (r cosφ·
+ r sinφ·
) = - ω²
,

a jego wartość wynosi

a_r = r ω² .

Całkowite przyspieszenie a = r

Gdy ε = const ⇒ ω = ω₀ + ε t,
;

kąt φ w radianach, ω w rad/s, ε w rad/s².

w_z

180°- α

α

α

φ

X

Z

β

α

w_x

w_y

Y

X

p

φ

w_y

w_x

w_xy

Y

α

β

γ

P

P'

O

s

P

P'

O

φ

φ

przemieszczenie wypadkowe

ruch 1.

przemieszczenie

ruch 2.

przemieszczenie

O

A

B

A

B

kierunek

zwrot

x

X

Y

P

y

v_m

v_o

d

A

α

v'_w

v_o

v'_m

B

punkt przyłożenia

„łańcuch”

O

v_m

v_o

d

A

B

O

z

φ

v_w

v_o

v_m

---