Do wykładu № 10

Pole magnetyczne. Indukcja magnetyczna. Siła Lorentza. Prawo Ampere'a. Prawo Biota - Savarta - Laplace'a. Diamagnetyki, paramagnetyki i ferromagnetyki. Podstawy teorii Maxwella. Prawo indukcji elektromagnetycznej. Układ równań Maxwella. Obwody prądu zmiennego - moc i rezonans.

1. Feynman R.P., Leighton R.B., Sands M. Feynmana wykłady z fizyki. - Warszawa: PWN, 1971. - W 5 t.

2. Resnik R., Holliday D. Fizyka. - Warszawa: WN PWN, 1998. W 2 t.

3. Bobrowski C. Fizyka - krótki kurs. - Warszawa: WNT, 2007.

Wykłady realizowany są w ramach projektu pt. „Mechatronika kierunkiem przyszłości - dostosowanie oferty edukacyjnej Uniwersytetu Kazimierza Wielkiego do potrzeb rynku pracy”, Działanie 4.1.1, Programu Operacyjnego Kapitał Ludzki, współfinansowanego ze środków Europejskiego Funduszu Społecznego”.

Zjawisko indukcji elektromagnetycznej

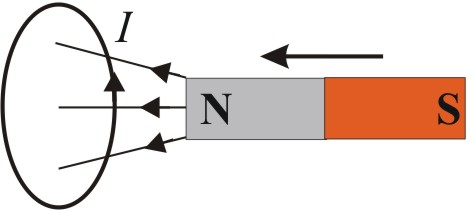
Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna

.

Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem N w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun N.

Reguła Lenza wynika również z bardzo ogólnej reguły przekory (Le Chatelier i Braun), która głosi, że układy fizyczne zachowują się przekornie. Układ fizyczny znajdujący się w stanie równowagi poddany działaniu czynnika zewnętrznego reaguje tak, żeby zmniejszyć wpływ tego czynnika i osiągnąć nowy stan równowagi możliwie niezbyt odległy od stanu równowagi wyjściowej. Zjawisko indukcji elektromagnetycznej jest jednym z wielu zjawisk fizycznych, których przebieg wynika z reguły przekory.

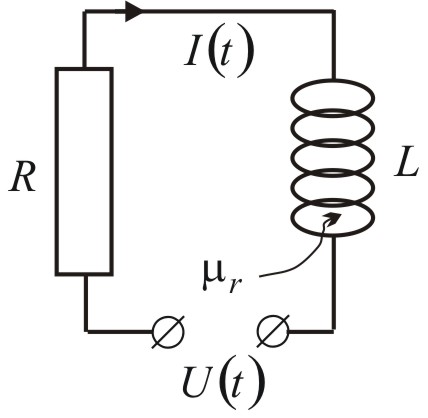
Zjawisko samoindukcji

Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie
, to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy
oraz wartość strumienia magnetycznego
przez powierzchnię
każdego zwoju, a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości

Zatem całkowita siła elektromotoryczna powstająca w zwojnicy jest równa

,

gdzie
jest ogólna liczbą zwojów w cewce.

Ponieważ

,

gdzie
— długość cewki (
— gęstość zwojów na jednostkę długości), to strumienia magnetycznego

.

Wówczas siły elektromotorycznej w każdym zwoju mamy

.

Dla cewki w całości

.

Otrzymany wynik przyjęto zapisywać w postaci

,

gdzie

nazywane jest indukcyjnością cewki.

Indukcyjności cewki
zależę od jej parametrów i określa zdolność do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość
można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość
).

Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność
obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego.

Energia pola magnetycznego

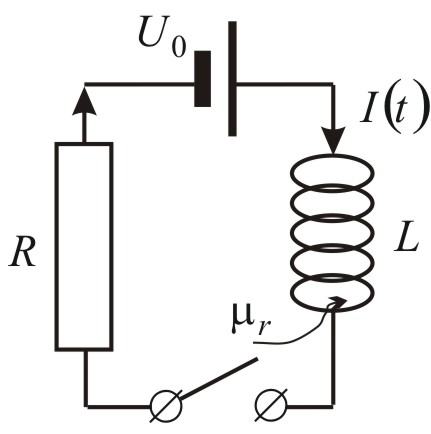
W chwili
zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie, wynikające z drugiego prawa Kirchhoffa

,

którego rozwiązaniem jest funkcja

,

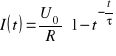
gdzie
jest stałą czasową procesu narastania natężenia prądu od zera do wartości wynikającej z prawa Ohma.

Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez

.

Iloczyn natężenia prądu i napięcia źródła
to moc źródła. Składnik
to moc w oporniku. Zatem wyrażenie

,

to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy.

Powyższe wyrażenie można zapisać w postaci (
)

.

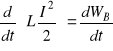
Skąd otrzymujemy wzór określający energię pola magnetycznego
wewnątrz zwojnicy

.

Jeśli wykorzystując wzory

i
,

to podstawiając otrzymamy

.

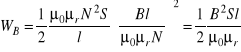
Ponieważ
jest objętością cewki, to dla gęstości energii pola magnetycznego znajdziemy

.

Zaznaczmy, że w przypadku ogólnym

.

Elektromagnetyczne drgania swobodne

Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne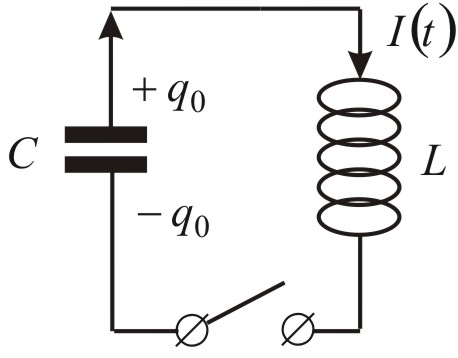
drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności
i kondensator o pojemności
.

W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem
. Gdy w chwili
zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji.

W takim obwodzie zachodzą procesy przekształcania energii pola elektrycznego kondensatora w energię pola magnetycznego cewki (i na odwrót).

Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa (prawo zachowania energii). Oznacza to, że spadek potencjału pola elektrycznego w obwodzie winien być równy zero, tzn.

,

gdzie
i
— napięcia na okładkach kondensatora i cewce indukcyjnej.

Napięcie na cewce indukcyjnej określa wzór

,

gdzie t — czas.

Po podstawieniu otrzymamy

.

Skorzystamy z definicji natężenie prądu w obwodzie

oraz definicji pojemności kondensatora C

,

z której

,

gdzie q ładunek kondensatora.

Ponieważ

,

to powyższe równanie
może być przepisane w postaci równania elektromagnetycznego oscylatora harmonicznego swobodnego

.

Rozwiązaniem tego równania, spełniającym warunki początkowe (fizyczne sformułowanie zagdnienia)

,
,

jest funkcja (sprawdzić podstawieniem)

,

gdzie

— częstotliwość kołowa lub częstość drgań swobodnych oraz wielkość
nazywamy amplitudą drgań, a argument funkcji kosinusa
— fazą drgań.

Wówczas okres

i częstotliwość drgań swobodnych (inaczej drgań własnych) obwodu LC

zależą od pojemności i indukcyjności obwodu.

Mając funkcję
można obliczyć napięcie na kondensatorze
, natężenie prądu
oraz napięcie na zwojnicy
.

Dla napięcia na kondensatorze mamy

.

Dla prądu

.

Dla napięcia na cewce

.

Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi
), zaś natężenie prądu jest przesunięte w fazie o
.

Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne — wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie
zaczepiony do sprężyny o współczynniku sprężystości
) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości.

Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy
, a zatem możemy obliczyć moc

,

gdzie
jest energia pola elektrycznego w kondensatorze.

Skąd

i

,

gdzie
jest stała całkowania.

Wówczas

.

Dla pola magnetycznego odpowiednio zapiszemy

,

gdzie
i
są mocą i energią pola magnetycznego w cewce.

Skąd

i

,

gdzie
jest stała całkowania.

Wówczas

.

Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o
.

Ponieważ, stałe całkowania według przyjętych warunków całkowania są równe zero
, to całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy

.

Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych, czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają.

Elektromagnetyczne drgania tłumione.

Obwód RLC drgań elektrycznych złożony jest z kondensatora o pojemności C, cewki o indukcyjności L i opornika o oporze R.

Rys. 1. Przełączenie kondensatora z obwodu ładowania do obwodu RLC

Rys. 2. Obwód RLC zaraz po dołączeniu naładowanego kondensatora

W takim obwodzie zachodzą procesy przekształcania energii pola elektrycznego kondensatora w energię pola magnetycznego cewki (i na odwrót), a także rozpraszania na oporach czynnych.

Załóżmy, że naładowany kondensator o pojemności
zaczyna się rozładowywać przez opór
i zwojnicę o indukcyjności
.

Zgodnie z drugim prawem Kirchoffa suma zmian potencjału na drodze zamkniętej jest równa zeru

, (1)

gdzie
,
i
— napięcia na okładkach kondensatora, cewce indukcyjnej i oporze.

Napięcie na cewce indukcyjnej określa się wzorem

, (2)

gdzie t — czas.

Natężenie prądu w obwodzie elektrycznym określa się przez prawo Ohma

, (3)

wówczas

. (4)

Po podstawieniu wyrazów (2) i (4) do równania (1) otrzymamy

. (5)

Skorzystamy z definicji natężenie prądu w obwodzie

oraz definicji pojemności kondensatora C

,

z której

,

gdzie q ładunek kondensatora.

Ponieważ

,

to równanie (5) może być przepisane w postaci

. (6)

Jeżeli do wzoru (6) podstawić zależność
, to otrzymamy równanie różniczkowe zmian wartości napięcia na kondensatorze

. (7)

Różniczkując równanie (6) względem czasu t i wykorzystując zależności

,
,
,

otrzymamy równanie różniczkowe dla natężenia prądu

. (8)

Poszukujemy rozwiązanie równania (6) w postaci

,

gdzie A i m - stałe.

Wstępnie obliczymy pochodne

,

i podstawimy do równania (6)

.

Współczynnik
nie może być równy zeru, ponieważ brak ładunku na kondensatorze oznaczałby, że nie zachodzą drgania w obwodzie. Także funkcja
nigdy nie równia się zero. Wobec tego przyrównujemy do zera sumę

.

Pierwiastki tego równania (według wiadomego wzoru dla pierwiastków równania algebraicznego
:
)

.

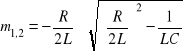
Należy przeanalizować trzy przypadki.

A. Jeżeli

,

to pierwiastki są rzeczywiste, ujemne i różne od siebie. Mówimy wtedy o obwodzie aperiodycznym.

B. Jeśli

,

to pierwiastki są rzeczywiste i równe sobie. Mówimy wtedy o obwodzie aperiodycznym krytycznym.

C. Jeżeli

,

to pierwiastki są zespolone o ujemnej części rzeczywistej. Mówimy wtedy o obwodzie drgającym (oscylacyjnym).

A. Obwód aperiodyczny. Wtedy każdemu pierwiastku rzeczy­wistemu
i
odpowiada swoje rozwiązanie równania (6):
i
.

Funkcję
i
są liniowo niezależne. Liniowa niezależność oznacza, że niema takiej liczby rzeczywistej
(
), żeby

Oprócz tego funkcję
i
, gdzie
i
są dowolne stałe, mówi się stałe całkowania, też będą rozwiązaniami równania (6).

Więc otrzymujemy następujące rozwiązanie ogólne (wzór określający zachowanie obwodu w przypadku aperiodycznym)

,

gdzie stałe
i
należę wyznaczyć z warunków początkowych.

Rys 3.  Przykładowe przebiegi napięcia na elementach R = 100 Ohm, L = 0,001 H  i C = 0,000001 F oraz prądu w obwodzie, gdy E = 10 V.

B. Obwód aperiodyczny krytyczny. W tym przypadku
i w jakości liniowo niezależnych rozwiązań przyjmujemy funkcję
i
(łatwo sprawdzić, że funkcja
jest rozwiązaniem równania). Wtedy otrzymujemy następujący wzór określający zachowanie obwodu

,

gdzie
i
są stałe całkowania, które wyznaczamy z warunków początkowych.

Rys 4. Przykładowe przebiegi napięcia na elementach R = 63,24555 Ohm, L = 0,001 H  i C = 0,000001 F oraz prądu w obwodzie, gdy E = 10 V.

C. Obwód drgający (oscylacyjny). Wprowadzając nowe ozna­czenia, a mianowicie

,

pierwiastki zapiszemy w postaci

,

gdzie
— jedynka urojona.

Oznaczając

,

otrzymujemy

,
.

Zatem ładunek kondensatora wyraża się wzorem

lub
.

Zgodnie ze wzorem Euler'a mamy

i
.

Wówczas

.

Oznaczając

,

otrzymujemy

. (9)

Stałe M i N wyznaczmy z warunków początkowych, a mianowicie

. (10)

Zatem w chwili początkowej na kondensatorze znajduje się maksymalny ładunek
. Z równania (9) dla
mamy
. Wobec tego
oraz

. (11)

Z definicji natężenie prądu mamy

. (12)

W chwili początkowej z tego równania dla
mamy
. Skąd

.

Podstawiając otrzymaną stałą N do równania (11) znajdziemy

, (13)

a z równania (12) odpowiednio

. (14)

Wyraz

przedstawia wartość maksymalną natężenia prądu (amplitudę) Zatem

. (15)

Biorąc pod uwagę, że
z równania (13) otrzymujemy przebieg napięcia na kondensatorze, a więc

, (16)

gdzie
— amplituda napięcia.

Rys 5. Przykładowe przebiegi napięcia na elementach R = 20 Ohm, L = 0,001 H  i C = 0,000001 F oraz prądu w obwodzie, gdy E = 10 V.

Elektromagnetyczne drgania wymuszone

Elektromagnetyczne drgania wymuszone można zaobserwować w obwodzie RLC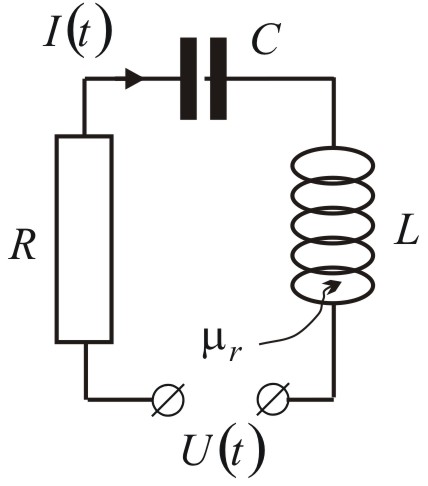
(zawierającym zwojnicę o indukcyjności
, kondensator o pojemności
oraz opornik o oporności
), do którego dołączone zostało zmienne źródło napięcia.

Jeśli ograniczymy się przypadkiem, że

,

to zgodnie z drugim prawem Kirchoffa mamy

,

gdzie
,
i
— napięcia na okładkach kondensatora, cewce indukcyjnej i oporze,
i
— amplituda i częstotliwość sinusoidalnego napięcia zewnętrznego.

Napięcie na cewce indukcyjnej określa się wzorem

,

gdzie t — czas.

Natężenie prądu w obwodzie elektrycznym określa się przez prawo Ohma

,

wówczas

.

Po podstawieniu tych wyrazów do wyjściowego równania otrzymamy

.

Skorzystamy z definicji natężenie prądu w obwodzie

oraz definicji pojemności kondensatora C

,

z której

,

gdzie q ładunek kondensatora.

Ponieważ

,

to równanie może być przepisane w postaci

.

Jeżeli do tego wzoru podstawić zależność
, to otrzymamy równanie różniczkowe zmian wartości napięcia na kondensatorze

.

Różniczkując poprzednie równanie względem czasu t i wykorzystując zależności

,
,
,

otrzymamy równanie różniczkowe dla natężenia prądu

.

W równaniu tym bezpośrednie parametry układu fizycznego, jakimi są w przypadku obwodu RLC: indukcyjność
, pojemność
i oporność
zostały zastąpione przez uniwersalne parametry występujące w opisie drgań harmonicznych dowolnego układu fizycznego (np. oscylator harmoniczny mechaniczny), a mianowicie przez częstość drgań własnych
i współczynnik tłumienia
.

Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji również sinusoidalnej, a zatem przewidujemy, że ładunek na kondensatorze będzie się zmieniać z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o
względem tego napięcia. Po podstawieniu przewidywanej funkcji
do równania i zażądaniu aby równanie to stało się tożsamością (funkcja
musi spełniać to równanie w każdej chwili czasu) otrzymamy wzory określające amplitudę ładunku
i przesunięcie fazowe
.

Przy ustalonych parametrach układu
,
,
(a więc również
i
) amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości
napięcia wymuszającego. Po przeprowadzeniu badania funkcji
można stwierdzić, że amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania
, gdy współczynnik tłumienia jest mniejszy od wartości granicznej (
).

Zjawisko wymuszania drgań z taką częstością, przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem. Rezonans w obwodzie RLC zachodzi przy częstości wymuszania
zwanej częstością rezonansową, gdy współczynnik tłumienia
jest mniejszy od wartości granicznej
. Gdy tłumienie jest większe (
) układu RLC nie udaje się wprowadzić w stan rezonansu.

Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami:

,
.

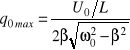
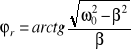
Szczególny przypadek rezonansu występuje w przypadku, gdy współczynnik tłumienia
. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych
i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym
. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną.

Graniczne wartości amplitudy drgań
i przesunięcia dla częstości wymuszania dążącej do zera wynoszą

,
.

Dla częstości znacznie przekraczających częstość własną, wartości graniczne amplitudy drgań i przesunięcia fazowego wynoszą

,
.

Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. parametry zredukowane:

— zredukowany współczynnik tłumienia;

— zredukowana częstość drgań;

— zredukowana amplituda drgań wymuszonych.

Po zastosowaniu powyższych podstawień wzory określające: amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmą postać

,
,
.

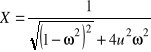
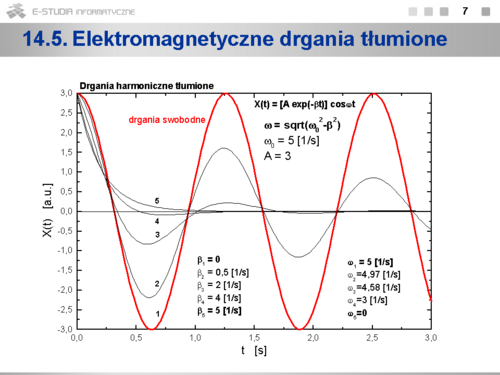
Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań
od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia
. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa
nie posiada maksimum).

Znając funkcję
można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego: napięcie na kondensatorze, natężenie prądu, napięcie na oporniku oraz napięcie na zwojnicy.

Niezależność amplitud ładunku i natężenia prądu oraz przesunięć fazowych względem napięcia wymuszającego oznacza, że zachodzą tzw. drgania ustalone. Układ fizyczny dopasowuje się do czynnika wymuszającego. Można łatwo wykazać, że podczas drgań ustalonych szybkość dostarczania energii przez źródło napięcia wymuszającego zrównuje się z szybkością strat energii na pracę prądu w oporniku i suma średniej energii pola elektrycznego w kondensatorze i średniej energii pola magnetycznego w zwojnicy jest stała (dla danej częstości wymuszania).

Drgania mechaniczne	Drgania elektromagnetyczne
siła harmoniczna	napięcie na kondensatorze
oscylator swobodny	oscylator swobodny
prędkość liniowa	natężenie prądu
rozwiązanie	rozwiązanie
położenie względem stanu równowagi	ładunek zgromadzony w kondensatorze
współczynnik sprężystości sprężyny	odwrotność pojemności kondensatora
masa ciała	indukcyjność zwojnicy
częstość drgań swobodnych	częstość drgań swobodnych
energia potencjalna	energia pola elektrycznego
energia kinetyczna	energia pola magnetycznego
drgania tłumione	drgania tłumione
współczynnik siły oporu	opór elektryczny
współczynnik tłumienia	współczynnik tłumienia
drgania wymuszone i tłumione	drgania wymuszone i tłumione

---