ANALIZA PRACY JEDNOWYMIAROWEGO UKŁADU REGULACJI AUTOMATYCZNEJ

Układem regulacji automatycznej nazywamy układ sterowania ze sprzężeniem zwrotnym, który (bez ingerencji człowieka — w przeciwnym razie byłby to układ regulacji ręcznej) ma za zadanie realizacje. odpowiednich przebiegów jednej lub kilku wielkości charakteryzujących proces, zwanych wielkościami regulowanymi.

Schemat blokowy układu regulacji automatycznej składa się z członu o transmitancji
reprezentującego obiekt regulacji i członu o transmitancji
reprezentującego regulator.

Rys. Różne postacie schematu blokowego jednowymiarowego układu regulacji
automatycznej: a) postać ogólna; b) uwzględnienie transmitancji od zakłóceń

Obiektem regulacji (krótko obiektem) nazywamy proces technologiczny lub urządzenie, w którym zachodzi proces podlegający regulacji, a regulatorem - urządzenie, które poprzez odpowiednią zmianę wielkości sterującej (sterowania) x(t) dąży do utrzymania wymaganej zmienności wielkości regulowanej y(t). Porównanie wielkości regulowanej y(t) z jej wartością zadaną y₀(t) (wielkością zadającą lub wielkością odniesienia) dokonuje się w węźle sumacyjnym. Różnicę
nazywamy uchybem regulacji. Układ regulacji pracuje dobrze, jeżeli mimo działających na obiekt zakłóceń
,
, ...,
uchyb regulacji e(t) jest możliwie mały (teoretycznie równy zeru). Wprowadzając transmitancje operatorowe
,
, ...,
dla poszczególnych zakłóceń
,
, ...,
możemy schemat blokowy tego układu przedstawić w postaci podanej na rys. b.

Ze schematu tego wynika następująca zależność między transformatami uchybu regulacji E(s), wartości zadanej wielkości regulowanej
i zakłóceń
,
, ...,

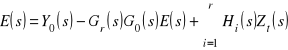
Skąd mamy

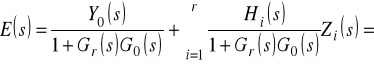
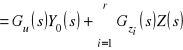
przy czym

jest transmitancją układu otwartego (układu z przerwaną pętlą sprzężenia zwrotnego), zaś

- transmitancją uchybową, określaną jako stosunek transformaty E(s) do
przy braku zakłóceń i zerowych warunkach początkowych i wreszcie

- transmitancją zakłóceniową (w układzie zamkniętym) określoną jako stosunek transformaty E(s) do
dla
i zerowych warunków początkowych.

Ze wzoru

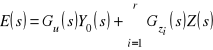
wynika, że dla dowolnej wartości
i dowolnych zakłóceń
,
, ...,
uchyb regulacji
jest równy zeru, jeżeli
. Wymaga to nieskończenie wielkiego współczynnika wzmocnienia układu otwartego. Przy wzroście tego współczynnika zwykle układy przechodzą ze stanu stabilnego do stanu niestabilnego. Projektant układu regulacji automatycznej musi zatem znaleźć rozwiązanie kompromisowe miedzy wymaganiami dokładności i stabilności regulacji.

Miarą dokładności statycznej (dokładności w stanie ustalonym) układu są wartości uchybu regulacji w stanie ustalonym.

Uchyb regulacji e(t) wywołany przez
można przedstawić w otoczeniu punktu
jako sumę szeregu nieskończonego o postaci

przy czym

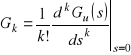
nazywamy współczynnikami uchybowymi.

Rozwijając w szereg Maclaurina transmitancję uchybową

i podstawiając do zależności:

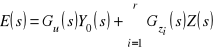
dla
otrzymamy:

Wzór:

jest oryginałem zależności:

,

słusznej w otoczeniu punktu
.

Wartości ustalone uchybu regulacji można również wyznaczyć na podstawie E(s) korzystając ze wzoru

wynikającego z twierdzenia o wartości końcowej obowiązującego w rachunku operatorowym.

Układami statycznymi nazywamy układy, których transmitancja układu otwartego
nie ma biegunów zerowych, a układami astatycznymi - układy, których transmitancja ta ma przynajmniej jednokrotny biegun zerowy. Rozróżnia się pojęcie statyzmu (lub astatyzmu) względem wartości zadanej i względem zakłóceń. Różnica w sformułowaniach wynika z różnych postaci transmitancji uchybowej

względem wartości zadanej i transmitancji zakłóceniowej

względem zakłóceń. Stopniem astatyzmu układu nazywamy krotność bieguna zerowego. Układ zamknięty jest układem astatycznym l-tego stopnia, jeżeli układ otwarty zawiera l połączonych łańcuchowo członów całkujących, a jego transmitancja ma postać

W tym przypadku współczynniki uchybowe
,
, ...,
są równe zeru, a
, i następne są różne od zera. Oznacza to, że układ astatyczny l-tego rzędu odtwarza z uchybem ustalonym równym zeru tylko te sygnały
, dla których
, dla

Na przykład układ statyczny (astatyczny zerowego stopnia
) dla
ma niezerowy uchyb w stanie ustalonym, zwany uchybem statycznym, określony wzorem

przy czym
jest współczynnikiem wzmocnienia układu otwartego.

Układ astatyczny pierwszego stopnia
dla
ma uchyb w stanie ustalonym równy zeru, a dla
uchyb niezerowy, zwany uchybem prędkościowym, określony wzorem

Uchyb regulacji
w stanie nieustalonym jest sumą składowej ustalonej e_u i składowej przejściowej

Podstawową miarą jakości układu regulacji jest czas regulacji t_r, określany jako czas od chwili pobudzenia (pojawienia się
) do chwili, gdy składowa przejściowa uchybu
zmaleje trwale poniżej założonej wartości
, przyjmowanej zwykle od 2 do 5% wartości początkowej lub maksymalnej (rys.).

Przykładowe przebiegi uchybu regulacji e(t) przy wymuszeniu skokowym:

a) przy skoku wartości zadanej; b) przy skoku zakłócenia

Inną miarą jakości odpowiedzi układu regulacji na wymuszenie jest przeregulowanie
określane wzorem (rys.)

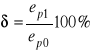
przy czym
jest wartością początkową lub maksymalną składowej przejściowej uchybu
, a
- najmniejszą wartością uchybu o znaku przeciwnym niż
.

Powyższe określenia mają sens dla wymuszeń będących, co najwyżej wielomianami (stopnia 0, l, 2,...) zmiennej t. W przypadku wymuszeń sinusoidalnych uchyb
ma przebieg również sinusoidalny.

KOREKCJA LINIOWYCH UKŁADÓW STACJONARNYCH

ISTOTA KOREKCJI ORAZ PODSTAWOWE RODZAJE REGULATORÓW I CZŁONÓW KOREKCYJNYCH

Przy projektowaniu układów regulacji automatycznej zagadnienie syntezy często sprowadza się do następującego zadania: Jest dany obiekt regulacji o znanej transmitancji operatorowej
. Należy zaprojektować układ regulacji tak, aby spełniał on warunek żądanej dokładności, dostatecznego zapasu stabilności i szybkości działania.

W najprostszym przypadku układu liniowego ciągłego jednej wielkości regulowanej, zadanie syntezy polega często na wyborze regulatora z danej klasy oraz doborze jego parametrów tak, aby jakość regulacji była zadowalająca w sensie określonego, najczęściej uproszczonego, wskaźnika jakości. Jako uproszczone wskaźniki jakości przyjmuje się dokładność statyczną oraz pewne wybrane parametry charakterystyki skokowej lub charakterystyk częstotliwościowych.

Podstawowymi parametrami charakterystyk częstotliwościowych układu otwartego
są: pulsacja (częstotliwość) graniczna modułu
określana równością:

lub

oraz pulsacja (częstotliwość) graniczna fazy (argumentu)
określana równością

Odchylenie logarytmicznej charakterystyki amplitudowej układu otwartego od wartości 0 dB dla pulsacji granicznej fazy
nazywamy zapasem modułu, a odchylenie logarytmicznej charakterystyki fazowej od wartości -180° dla pulsacji granicznej modułu
- zapasem fazy

Zapasy modułu i fazy określają zapas stabilności układu zamkniętego.

Ważnym parametrem charakterystyk częstotliwościowych układu zamkniętego jest pulsacja (częstotliwość) rezonansowa
określana jako pulsacja, dla której moduł transmitancji widmowej układu zamkniętego
osiąga wartość maksymalną. Wartość maksymalna modułu tej transmitancji, zwana modułem rezonansowym (współczynnikiem oscylacji)

jest miarą zapasu stabilności układu.

Regulator proporcjonalny (typu P) wytwarza sygnał sterujący
liniowo zależny od uchybu regulacji
. Zapewnia on dość szybką regulację przy niezbyt dużej dokładności statycznej.

Regulator całkowy (typu I) wytwarza sygnał sterujący proporcjonalny do całki uchybu regulacji
. Zaletą tego regulatora jest astatyzm układu, a wadą wydłużenie czasu regulacji. Dla osiągnięcia stosunkowo szybkiej regulacji przy zachowaniu astatyzmu stosuje się regulatory proporcjonalno-calkotoe (typu PI). Jeżeli szybkość regulatora PI jest niewystarczająca, można ją zwiększyć przez dodanie składowej proporcjonalnej do pochodnej uchybu regulacji czyli przez zastosowanie regulatora proporcjonalno-całkowo-różniczkowego (typu PID). Działanie różniczkowe regulatorów wpływa również zwykle korzystnie na stabilność układu.

W tablicy podano transmitancje operatorowe, równania, charakterystyki skokowe, charakterystyki amplitudowo-fazowe oraz charakterystyki logarytmiczne amplitudowe i fazowe regulatorów liniowych ciągłych typu P, I, PI, PD i PID.

Typ regulatora	Transmitancja operatorowa i równanie regulatora	Charakterystyka skokowa	Charakterystyka amplitudowo-fazowa	Charakterystyka logarytmiczna
								amplitudowa	fazowa
Proporcjonalny P
Całkowy I
Proporcjonalno - całkowy PI
Proporcjonalno - różniczkowy PD
Proporcjonalno - całkowo - różniczkowy PID

Łatwo wykazać, że transmitancja operatorowa układu z ujemnym sprzężeniem zwrotnym, zawierającego w torze głównym człon bezinercyjny o bardzo dużym współczynniku wzmocnienia k (teoretycznie
), a w pętli sprzężenia zwrotnego człon o transmitancji
jest równa w przybliżeniu G_r(s).

Układy równoważne dla

Zasada ta jest wykorzystywana przy budowie regulatorów. Aby zbudować np. regulator PI, należy w pętli sprzężenia zwrotnego układu zawierającego w torze głównym człon bezinercyjny o bardzo dużym współczynniku wzmocnienia k umieścić człon różniczkujący rzeczywisty o transmitancji operatorowej
.

Właściwości rzeczywistych regulatorów różnią się od idealnych przede wszystkim występowaniem dodatkowych inercji i ograniczeń modułu w zakresie małych i dużych częstotliwości.

Jeżeli użycie jednego z podstawowych regulatorów nie zapewnia wystarczającej jakości regulacji, to dla poprawy do układu wprowadzamy dodatkowe człony dynamiczne zwane członami korekcyjnymi. Korekcją natomiast nazywamy postępowanie polegające na wprowadzaniu do układu dodatkowych członów o strukturze i parametrach tak dobranych, aby nowo powstały układ miał pożądane właściwości.

WYBÓR RODZAJU I NASTAW REGULATORA

Podstawowym warunkiem trafnego wyboru rodzaju regulatora jest znajomość, choćby przybliżona, własności obiektu regulacji. Zgodnie z ogólną klasyfikacją, wyróżnimy obiekty statyczne i astatyczne, których charakterystyki skokowe pokazano na rysunku

Charakterystyki skokowe obiektów: a) statycznych, b) astatycznych

Przybliżone transmitancje opisujące te grupy obiektów przedstawia się najczęściej w postaci

gdzie:

- zastępcze opóźnienie obiektu,

T - zastępcza stała czasowa obiektu,

k' - jednostkowy współczynnik proporcjonalności obiektu.

Przykładowo, przeciętne wartości
i T dla kilku typowych procesów są następujące:

1) procesy zmian temperatury (obiekty statyczne)

• w małych piecach laboratoryjnych
  ,
  ,

• w większych piecach żarowych
  ,
  ,

• w kolumnach destylacyjnych
  ,
  ,

• w pomieszczeniach ogrzewanych
  ,
  ;

2) procesy zmian poziomu wody (obiekty astatyczne)

• w walczaku kotła parowego
  ,
  ,
  .

W ramach naszych wykładów omówione będą tylko zasady wyboru rodzaju i nastaw regulatorów ciągłych PDI, które z dość dobrym przybliżeniem można traktować jako elementy liniowe. Zakres zastosowań tych regulatorów łatwo ocenić na podstawie podawanych zwykle zaleceń:

a) dla
można zastosować regulator dwupołożeniowy,

b) dla
należy zastosować regulator o działaniu ciągłym,

c) dla
należy zastosować regulator impulsowy.

Najczęściej spotykane wartości
mieszczą się w przedziale 0,2-0,7 i dlatego regulatory o działaniu ciągłym (PID) są najbardziej rozpowszechnione w przemyśle.

Potrzebne własności dynamiczne regulatora można najlepiej określić znając charakterystykę częstotliwościową obiektu. Na rysunku przedstawiono przykładowo charakterystyki amplitudowo-fazowe dwóch obiektów (we współrzędnych Blacka), do których zastosować należy w przypadku
a) regulator PI, a w przypadku b) regulator PD.

Logarytmiczne charakterystyki amplitudowo-fazowe obiektów:

a) przypadek, gdy skuteczny będzie regulator PI,

b) przypadek, gdy skuteczny będzie regulator PD

Uzasadnienie takiego wyboru wynika z warunków stabilności i jakości dynamicznej układu. Wypadkowa charakterystyka amplitudowo-fazowa układu otwartego musi pozostawiać po prawej stronie początek układu współrzędnych, idąc w stronę rosnących
. Jeżeli pamiętamy, że regulator PI wprowadza ujemne przesunięcie fazowe, a jego moduł maleje ze wzrostem częstotliwości, natomiast regulator PD wprowadza dodatnie przesunięcie fazowe, a jego moduł rośnie ze wzrostem częstotliwości, to zasada wyboru regulatora staje się oczywista.

Dokładniejsza analiza współpracy regulatora z obiektem prowadzi ponadto do następujących wniosków:

• regulator PI zapewnia dobrą jakość regulacji tylko przy zakłóceniach o małych częstotliwościach;

• regulator PD zapewnia szersze pasmo regulacji niż regulator PI, ale z gorszą jakością regulacji przy małych częstotliwościach;

• regulator PID łączy zalety obu poprzednich regulatorów.

Należy także brać pod uwagę, że stosowanie akcji różniczkującej wzmacnia wszelkie szumy przetwornika pomiarowego, a ponadto przynosi niewielkie korzyści dla
.

Na podstawie rozważań teoretycznych, badań modelowych i doświadczeń eksploatacyjnych opracowano wiele reguł nastawiania regulatorów według żądanych cech przebiegu przejściowego. Wyróżnia się przy tym najczęściej następujące cechy:

a) przebieg aperiodyczny, minimum
,

b) przebieg oscylacyjny z przeregulowaniem około 20%, minimum
,

c) przebieg z minimum całki kwadratu odchylenia regulacji.

Obecnie przedstawię niektóre, prostsze zasady doboru nastaw regulatorów przemysłowych. Wśród praktyków najbardziej są rozpowszechnione reguły doświadczalnego nastawiania regulatorów opracowane przez Zieglera i Nicholsa, które prowadzą do uzyskania przebiegów przejściowych z przeregulowaniem około 20% i minimum czasu regulacji
(przypadek b). Nastawianie przeprowadza się już po zainstalowaniu regulatora w układzie. Kolejność postępowania przy stosowaniu tych reguł jest następująca:

1. Należy nastawić regulator na działanie tylko proporcjonalne (P). Działania całkujące i różniczkujące powinny być wyłączone przez nastawienie
oraz
.

2. Należy zwiększać wzmocnienie proporcjonalne
regulatora, aż do wystąpienia oscylacji niegasnących w układzie (granica stabilności).

3. Następnie należy zmierzyć okres tych oscylacji
, a na skali regulatora należy odczytać krytyczne wzmocnienie proporcjonalne
, przy którym one wystąpiły.

4. Zależnie od typu regulatora, należy przyjąć nastawy

dla regulatora P:
;

dla regulatora PI:
,
;

dla regulatora PID:
,
,
.

Warto zwrócić uwagę na zbieżność reguł Zieglera—Nicholsa z powszechnym wymaganiem zapasu modułu równego 6dB. Zmniejszenie wzmocnienia układu do połowy wzmocnienia krytycznego, przy którym układ znajduje się na granicy stabilności, odpowiada właśnie wprowadzeniu zapasu modułu 6 dB.

Orientacyjne zestawienie obiektów, dla których można dobrać optymalne w podanym wyżej sensie (tzn.
) nastawy przeciętnego regulatora PID, na rysunku - obszar objęty linią kreskowana.

Zestawienie obiektów, dla których można dobrać optymalne
(w sensie
minimum
) nastawy regulatora PID

Uwzględniono jedynie wartość zastępczej stałej czasowej T oraz stosunek
. Wartości wzmocnień (lub ogólniej współczynników proporcjonalności) poszczególnych obiektów nie brano pod uwagę, gdyż prawie zawsze można je we właściwy sposób modyfikować, np. przez zmianę zakresu pomiarowego. Obszar ten jest nieco większy dla nowoczesnych regulatorów pneumatycznych i elektronicznych, które mają szerszy zakres nastaw. Odpowiednie obszary obiektów można zaznaczyć dla nastaw optymalnych w sensie
,
lub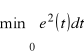
. Łącznie regulatory PID obejmą znaczną większość obiektów, dla których
.

W przypadku gdy wartości
,
i
obiektu są znane, bardzo wygodne jest korzystanie z tablic określających zarówno optymalne nastawy regulatora, jak i odpowiadające im podstawowe wskaźniki przebiegu przejściowego w układzie. W tablicy zestawiono dane dotyczące układów z obiektami statycznymi i astatycznymi, przy czym k_r oznacza wypadkowe wzmocnienie całego zespołu regulującego, a więc regulatora łącznie z przetwornikiem pomiarowym i ewentualnie innymi elementami występującymi w torze sprzężenia zwrotnego (np. blokiem przeliczającym lub siłownikiem, chociaż ten ostatni częściej włączany jest do obiektu regulacji). Jeżeli chcemy zatem określić wzmocnienie
regulatora, to wzmocnienia pozostałych elementów zespołu regulującego musza być znane.

Rodzaj przebiegu przejściowego	Rodzaj regulatora	Obiekt statyczny					Obiekt astatyczny
				Optymalne nastawy regulatora			Wskaźnik przebiegu przejściowego		Optymalne nastawy regulatora			Wskaźnik przebiegu przejściowego
		P	0,3	-	-	4,5		0,37	-	-	5,5	2,7
		PI	0,6	0,8+0,5	-	8		0,46	5,75	-	13,2	1,9
		PID	0,95	2,4	0,4	5,5		0,65	5,0	0,23	9,8	1,38
		P	0,7	-	-	6,5		0,7	-	-	7,5	1,43
		PI	0,7	1+0,3	-	12		0,7	3,0	-	15	1,62
		PID	1,2	2,0	0,4	7		1,1	2,0	0,37	12	1,12
		PI	1,0	1+0,35	-	16		1,05	4,3	-	18	1,44
		PID	1,4	1,3	0,5	10		1,37	1,6	0,51	15	1,03

Przedstawione zasady określania rodzaju i nastaw regulatora w układach jednoobwodowych znajdują również zastosowanie w kaskadowych układach regulacji, jedynie z tą różnicą, że są tam realizowane dwustopniowo.

W pierwszej kolejności wybiera się regulator pomocniczy, najczęściej w postaci regulatora P, gdyż działanie proporcjonalne jest konieczne dla linearyzacji charakterystyki statycznej części
obiektu (często główny powód wprowadzania regulacji kaskadowej!) i częściowej neutralizacji własności dynamicznych
. Odchylenia statyczne wielkości pomocniczej
nie są zwykle istotne, a więc dodawanie działania I nie jest potrzebne, mogłoby nawet być szkodliwe dla stabilności układu, jeżeli regulator główny też ma działanie całkujące. Dodanie działania D może być celowe tylko w tych przypadkach, kiedy część
obiektu nie stanowi wystarczającego filtru dla zakłóceń o dużych częstotliwościach. Wzmocnienie regulatora P wybiera się według, reguł Zieglera-Nicholsa lub kryterium
.

W drugiej kolejności dobiera się regulator główny, zwykle PI lub PID, gdyż istotne jest zmniejszenie do minimum odchylenia statycznego głównej wielkości regulowanej, y. Układ należy wówczas traktować jako jednoobwodowy, z obiektem regulacji zmodyfikowanym i dobór nastaw jest zgodny z podanymi wcześniej regułami.

	96
		Wykład Podstawy Automatyki prof. dr hab. inż. Stanisław Płaska