Istnieje ścisłe powiązanie pomiędzy wskaźnikami i tablicami.
Jeszcze raz: Wskaźniki
Istnieje ścisłe powiązanie pomiędzy wskaźnikami i tablicami.
Przykład:
double *ws, Tt[4]={3.15, 5.64, 7.67, 9.11} ;
ws=Tt
.........................
W przykładzie wskaźnik ws otrzymuje adres pierwszego elementu tablicy Tt.
Aby przykładowo odwołać się do 3 elementu tablicy Tt, można albo napisać:
Tt[2]
albo
*(ws+2) - obie instrukcje zwracają 3 element.
tzn. Tt[2]=7.67, ale również *(ws+1)= 7.67
Natomiast nie używając nawiasów w powyższym zapisie otrzymamy:
*ws+1= 4.15 /* bo jest to 3.15 +1*/
Wykorzystanie wskaźników przy odwoływaniu się do elementów tablicy daje szybszy kod!
#include <stdio.h>
void main()
{
char *te, tab[14]="Programowanie";
te=tab;
for (int i=0;i<14;i++)
printf ("%c",tab[i]); // wydruk tablicy znakowej tab
printf ("\n\n");
while (*te) printf("%c",*te++); // wydruk tablicy znakowej tab przy
// wykorzystaniu wskaźnika te
printf ("\n\n");
}
Przykład błędnej i
int main()
{
int x,*p;
x=10;
*p=x
}
poprawnej inicjalizacji wskaźnika:
int main()
{
int x,*p;
x=10;
p=&x
}
Dynamiczne alokowanie tablic - dc. Przykład
#include <stdio.h>
#include <stdlib.h>
int potega(int,int);
void main()
{
int (*p)[10];
int i,j;
p=(int(*)[10]) malloc(40*sizeof(int));
if (!p)
{
printf("Pobranie pamieci nie udalo sie\n");
exit(1);
}
for(j=1;j<11;j++)
for(i=1;i<5;i++)
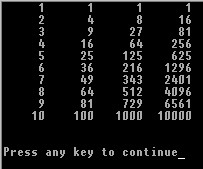
p[i-1][j-1]=potega(j,i);
for(j=1;j<11;j++)
{
for(i=1;i<5;i++)
printf("%10d ",p[i-1][j-1]);
printf("\n");
}
printf ("\n\n");
}
potega(int a, int b)
{
int k=1;
for ( ; b ; b-- ) k=k*a;
return k;
}
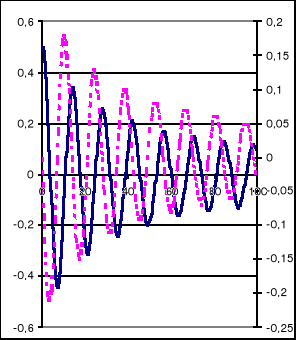
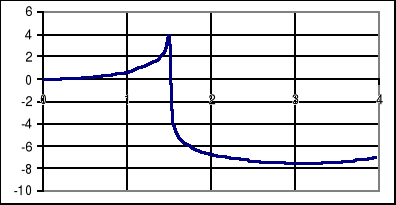
Napisać program wyznaczający krzywą rozpoczynająca się w początku układu współrzędnych dla której kąt pomiędzy styczną do krzywej a osią x równy jest:
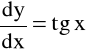
wartości współrzędnej x
#include<stdio.h>
#include<math.h>
double Runge_Kutta(double,double,double);
double f(double,double);
void main()
{
double x,y,h;
FILE *f;
int n,i;
f=fopen("rkx.dat","w");
h=0.05;
x=0;y=0;n=80;
fprintf(f,"%6.2f %8.2f\n",x,y);
for (x=h,i=1;i<n;x+=h,i++)
{
y=Runge_Kutta(x,y,h);
fprintf(f,"%6.2f %8.2f\n",x,y);
printf("%6.2f %8.2f\n",x,y);
}
}
double Runge_Kutta(double x,double y,double h)
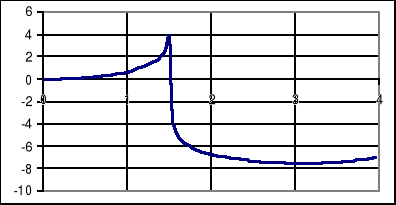
{
double k0,k1,k2,k3;
k0=h*f(x,y);
k1=h*f(x+0.5*h,y+0.5*k0);
k2=h*f(x+0.5*h,y+0.5*k1);
k3=h*f(x+h,y+k2);
return y+(k0+2*k1+2*k2+k3)/6;
}
double f(double x,double y)
{
return tan(x);
}
Procedura Newtona - rozwiązywanie równań różniczkowych 1 rzędu
y'=f(x,y)
czyli (numerycznie ): 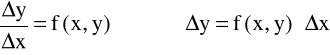
ponieważ : ![]()
więc: ![]()
Napisać program obliczający zachowanie się masy połączonej sprężyną z podłożem i równolegle tłumikiem hydraulicznym. Należy w kolejnych chwilach czasu określić położenie i prędkość masy.
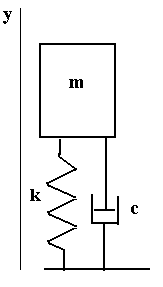
Równanie opisujące ruch masy:
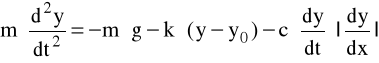
w stanie równowagi:
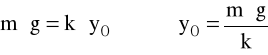
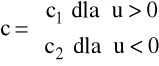
podstawiając: 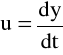
Otrzymuje się układ równań: 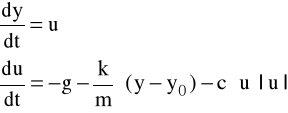
Wczytywane dane:
m, g, k, c1, c2, ypocz, Δt i tkoń
#include <stdio.h>
#include <math.h>
double f1(double);
double f2(double,double, double);
double g=9.81,m=2,k=0.4;
double c1=0.5, c2=0.2;
double ypocz=0.5;
double dt=0.5,tk=100;
void main()
{
FILE *f;
f=fopen("masa.dat","w");
double yr,y,u=0,t=0;
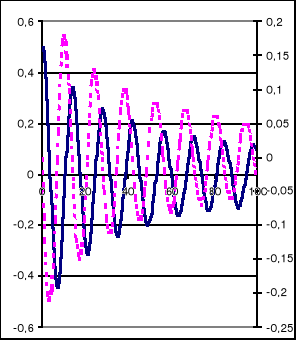
yr=m*g/k;
y=ypocz;
while (t<tk)
{
fprintf(f,"%4.1f %6.2f %6.2f\n",t,y,u);
printf("%4.1f %6.2f %6.2f\n",t,y,u);
y=y+f1(u)*dt;
u=u+f2(y,yr,u)*dt;
t=t+dt;
}
}
double f1(double u)
{
return u;
}
double f2(double y,double yr, double u)
{
double c;
if (u>0) c=c1; else c=c2;
return -g-k/m*(y-yr)-c*u*fabs(u);
}
Wykorzystać metodę Newtona do obliczenia wartości funkcji uwikłanej: F(x,y)=0. Tzn. napisać program, który umożliwia dla każdego x z dziedziny funkcji obliczenie wartości y.. Obliczenia prowadzić następująco:
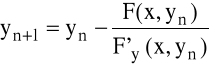
![]()
gdzie F'y(x,y) jest cząstkową pochodną funkcji po y.
Program wykorzystać do obliczenia wartości funkcji:
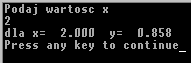
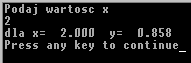
x*exp(y)-x*y-3=0 dla x=2
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
double pochodna(double,double,double);
double fun(double,double);
void main()
{
double h,p=1,x,y=1,eps=1e-8;
printf("Podaj wartosc x\n");
scanf("%lg",&x);
h=1e-6*x;
while (fabs(p)>eps)
{
p=fun(x,y)/pochodna(h,x,y);
y=y-p;
}
printf("dla x=%7.3f y=%7.3f\n",x,y);
return;
}
double pochodna(double h,double x, double y)
{
return (fun(x,y+h)-fun(x,y))/h;
}
double fun(double x, double y)
{
return x*exp(y)-x*y-3;
}
INFORMATYKA WYKŁAD 8 Temat: Język C 6
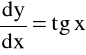
Przypomnienie: wskaźnik musi
przed jego użyciem zostać
zainicjowany tzn. musi zacząć
wskazywać na jakiś adres w
pamięci
To jest Tt[0] - pierwszy element
Trzeci element
tablicy czyli Tt[2]