Operat hydrologiczny dla potrzeb projektowania obiektów hydrometrycznych
WYKONALI:
**
**
CZĘŚĆ I
OPRACOWANIE I WYZNACZANIE CHARAKTERYSTYKI KRZYWEJ PRZEPŁYWU
1.1 Wstęp
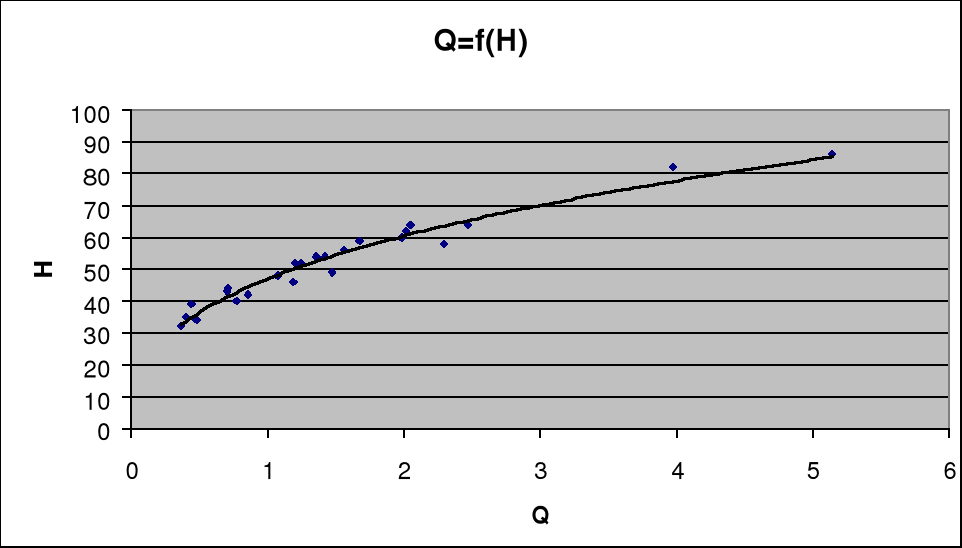
Krzywa przepływu przedstawia związek regresyjny pomiędzy zmierzonymi wartościami natężenia przepływu i stanu wody Q=f(H). Krzywą przepływu wyznacza się na podstawie wyników jednoczesnych pomiarów natężenia przepływu i stanów wody. Punkty te tworzą tzw. chmury punktów układających się z pewnym rozrzutem wynikającym z błędów przypadkowych, jakimi są obarczone wyniki pomiarów przepływów i stanów wody.
W celu wyznaczenia krzywej przepływu zastosowaliśmy analityczną i graficzną metodę aproksymacji.
Naszą krzywą przepływu wyznaczymy dla danych pomiarów z lat 1962-1980 w przekroju hydrometrycznym Mościsko na rzece Piława.
1.2 Wybranie punktów jednorodnych
Z 60 punktów niejednorodnych wybraliśmy 25 jednorodnych. W doborze tych punktów sugerowaliśmy się wartością β (tj. różnica pomiędzy H , a Tmax ), tak aby była dodatnia.
W tabeli 1. zestawione jest 25 jednorodnych punktów pomiarowych.
Tab.1.
Lp. |
Przekrój |
Data |
Stan wody |
Objętość przepływu |
Głębokość max |
|
|
hydrometryczny |
pomiaru |
H |
Q |
Tmax |
β |
- |
- |
- |
[cm] |
[m3/s] |
[cm] |
[cm] |
1 |
Mościsko |
24.01.1964 |
36 |
0,365 |
27 |
9 |
2 |
|
30.11.1962 |
37 |
0,481 |
26 |
11 |
3 |
|
23.09.1971 |
35 |
0,401 |
28 |
7 |
4 |
|
25.06.1965 |
39 |
0,437 |
26 |
13 |
5 |
|
26.01.1966 |
40 |
0,768 |
30 |
10 |
6 |
|
18.08.1966 |
42 |
0,855 |
40 |
2 |
7 |
|
13.10.1975 |
43 |
0,700 |
32 |
11 |
8 |
|
5.09.1975 |
44 |
0,708 |
40 |
4 |
9 |
|
19.09.1966 |
46 |
1,19 |
46 |
0 |
10 |
|
21.01.1980 |
48 |
1,07 |
34 |
14 |
11 |
|
16.03.1972 |
49 |
1,47 |
44 |
5 |
12 |
|
7.08.1979 |
52 |
1,24 |
48 |
4 |
13 |
|
13.11.1979 |
52 |
1,20 |
48 |
4 |
14 |
|
9.06.1978 |
54 |
1,42 |
54 |
0 |
15 |
|
9.10.1979 |
54 |
1,36 |
42 |
12 |
16 |
|
29.06.1977 |
56 |
1,56 |
38 |
18 |
17 |
|
8.05.1969 |
58 |
2,29 |
52 |
6 |
18 |
|
21.03.1980 |
59 |
1,67 |
48 |
11 |
19 |
|
20.01.1965 |
60 |
1,98 |
54 |
6 |
20 |
|
5.02.1980 |
62 |
2,01 |
50 |
12 |
21 |
|
6.11.1964 |
64 |
2,05 |
56 |
8 |
22 |
|
15.04.1965 |
64 |
2,04 |
58 |
6 |
23 |
|
6.09.1966 |
64 |
2,47 |
64 |
0 |
24 |
|
3.06.1968 |
82 |
3,97 |
74 |
8 |
25 |
|
18.06.1972 |
86 |
5,14 |
84 |
2 |
Analityczna metoda aproksymacji krzywej przepływu
Najczęściej krzywą przepływu opisuje się jako funkcję potęgową
Q = α(H - β)n,
gdzie:
α, n - są to parametry funkcji o dodatnich wartościach rzeczywistych
β - jest to parametr, który odpowiada stanowi Hd na wodowskazie, przy którym Q = 0 (punkt denny krzywej przepływu).
Wartość β obliczamy jako średnią arytmetyczną z różnic stanu wody Hi, zmierzonego podczas i-tego pomiaru natężenia przepływu, oraz głębokości maksymalnej Tmax,i obliczonych na podstawie k wyników pomiarów stanu wody ze strefy niskich i średnich:
β = ![]()
.
Dla 10 najniższych stanów wody policzyliśmy wartość średnią β. W naszym przypadku wyniosła: βśr = 12.
Wartości parametrów α i n równania krzywej przepływu wyznaczamy metodą najmniejszych kwadratów. W tym celu logarytmujemy obustronnie równanie i po zastosowaniu metody najmniejszych kwadratów uzyskujemy układ dwóch równań, który przekształcamy do postaci wzorów na poszukiwane wartości parametrów.
Otrzymujemy:
n = 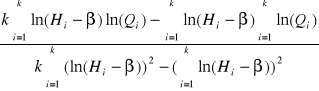
α = exp(![]()
Wartości α zawierają się w przedziale ![]()
, natomiast n w przedziale ![]()
W naszym przypadku α = 2,36*10-4, a n = 2,27.
Ekstrapolacja krzywej przepływu
Do tej pory w celu wyznaczenia krzywej przepływu stosowaliśmy metodę aproksymacji punktów pomiarowych w zakresie objętym pomiarami. W zależności od strefy stanu często brak jest pomiarów lub liczba jest ich bardzo mała (dotyczy to zwłaszcza stanów wysokich i dolną strefę stanów niskich).Ekstrapolacja krzywej przepływu ma ograniczony zakres, stąd przeprowadzamy ją w niewielkim zakresie (nie przekraczającym łącznie w dół i w górę 20% zakresu pomiarowego.
![]()
W naszym przypadku:
![]()
![]()
![]()
![]()
Ta zależność nie jest spełniona, stąd należałoby wyznaczyć przepływ Q dla Hmax lub Hmin.
W tym celu mierzymy spadek zwierciadła wody I, określając promień hydrauliczny Rh (w korytach szerokich i płytkich może być zastąpiony głębokością średnią) .
Przepływ Q obliczamy ze wzoru Chezy'ego:
Q = VF = c![]()
,
gdzie:
c - współczynnik, który określa się według zależności Manninga:
c = ![]()
,
gdzie:
n - współczynnik szorstkości określany na podstawie tabeli.
Włączamy ten punkt (jako jednorodny) do punktów pomiarowych i na nowo ustalamy krzywą i powtórnie ekstrapolujemy ją.
Możemy ekstrapolować o 0,1 w górę i 0,1 w dół krzywą przepływu. W naszym przypadku różnica pomiędzy Hpom.,min , a Hobs.,min jest niewielka stąd najlepiej jest dokonać ekstrapolację o 20% w górę. Natomiast wartość β przyjąć jako minimalny stan wody, a aproksymowaną krzywą przepływu poprowadzić do punktu β (przepływ równy 0). Zobrazowane jest to dokładnie na wykresie krzywej przepływu.
Część II
Rzeka: Wisła
Wodowskaz: Szczucin
1. Wyznaczenie przepływów głównych I i II rzędu
a) Przepływy główne I rzędu.
Wyznaczenie przepływów głównych I rzędu jest to wyznaczenie wielkości: maksymalnej, średniej, minimalnej i środkowej na podstawie ciągu codziennych przepływów, w określonym przekroju i z pewnego okresu czasu.
Przepływem maksymalnym nazywa się ten, o największej, w danym okresie, wielkości w [m3/s]. Wartość średnia jest to średnia arytmetyczna obliczana z całego zbioru pomiarów. Przepływem minimalnym nazywany jest najmniejszy spośród wszystkich niżówek z danego okresu. Środkowy wyraz ciągu przepływów uporządkowany rosnąco (lub malejąco) jest to wartość środkowa (zwyczajna).
W naszej pracy skupiliśmy się na wyznaczeniu następujących wielkości przepływów głównych I rzędu:
największej (WQ)
najmniejszą (NQ)
średnią (SQ)
Określiliśmy te wartości na podstawie danych dotyczących roku 1961, w przekroju Szczucin na rzece Wiśle. W tym celu sporządziliśmy wykres graficzny (Rys.1.1.) ilustrujący skalę zjawiska w odniesieniu do całego, wybranego przez nas, roku hydrologicznego (tj. od Listopada do Października).
Ponieważ zamieszczenie w tym miejscu wyżej wymienionych danych liczbowych nie wydaje się nam celowe, znajdują się one w załączniku nr 1a, na końcu tego opracowania.
Na podstawie wykresu, porównując z danymi liczbowymi (zał.1a.), wyznaczyliśmy następujące wartości przepływów głównych I rzędu:
WQ1961 = 455 [m3/s]
NQ1961 = 57 [m3/s]
SQ1961 = 170,4 [m3/s]
W 1961 roku maksymalny przepływ rzeką Wisłą, na przekroju Szczucin, wystąpił 2.04 w wielkości 455 [m3/s]. Minimalny przepływ - 57 [m3/s] - odnotowano dwa razy: 10 dnia i 27 dnia Października. Wartość średnia znalazła się w wielkości 170,4 [m3/s].
b) Przepływy główne II rzędu.
Zadaniem w tej części było wyznaczenie dwunastu następujących przepływów głównych drugiego rzędu:
WWQ WSQ WNQ
SWQ SSQ SNQ
NWQ NSQ NNQ
Na podstawie danych (zał.1b.) opisujących przepływy główne pierwszego rzędu wyznaczyliśmy wartości przepływów głównych II rzędu. Okres dla którego określiliśmy te wartości to wielolecie 1961-1990.
W tym celu sporządziliśmy 3 wykresy, które przedstawiają:
przepływy główne drugiego rzędu dla przepływów maksymalnych rocznych (Rys.1.2.)
przepływy główne drugiego rzędu dla przepływów średnich rocznych (Rys.1.3.)
przepływy główne drugiego rzędu dla przepływów minimalnych rocznych (Rys.1.4.).
Na podstawie sporządzonych wykresów, porównując także z danymi liczbowymi (zał.1b.), wyznaczyliśmy wartości przepływów głównych drugiego rzędu, które umieszczone są w tablicy 1.1.
Tablica 1.1. Przepływy główne II rzędu z wielolecia 1961-90
WWQ |
4150,0 |
WSQ |
343,9 |
WNQ |
124,0 |
|
|
|
|
|
|
SWQ |
1584,1 |
SSQ |
238,2 |
SNQ |
84,8 |
|
|
|
|
|
|
NWQ |
455,0 |
NSQ |
145,1 |
NNQ |
57,0 |
|
|
|
|
|
|
* * *
2. Przepływy o oznaczonym czasie trwania.
W celu znalezienia, jak również zobrazowania na wykresach, wielkości przepływów o oznaczonym czasie trwania wykonaliśmy następujące „kroki”:
ustaliliśmy okres podstawowy T równy 1 rok.
dla N lat, gdzie N = 3
wyznaczyliśmy 3 lata, porównując SSQ z SQ w danym roku; rok, w którym ta różnica była najmniejsza przyjęliśmy za środkowy.
SSQ = 238,2 [m3/s]
SQ1971 = 238,0 [m3/s]
To trzylecie to lata: 1970, 1971 i 1972.
określiliśmy:
Qmin, 1970-72 = 75,8 [m3/s]
Qmax, 1970-72 = 4150,0 [m3/s]
następnie wyznaczyliśmy liczbę przedziałów r:
an = Qmax/Qmin = 54,749
5,5 * ln an < r < 10,5 * ln an
22 < r < 42
przyjęliśmy liczbę przedziałów r = 32
wykorzystując poniższe wzory określiliśmy dolne granice poszczególnych przedziałów:
Qi = Qmin * an (i-1/r), i=1,2,...,r
sprawdziliśmy, że zachodzi:
0,1*Qi < Qi < 0,2*Qi , i=1,2,...,r
policzyliśmy liczbę wystąpień w przedziale, dla wszystkich 3 lat; przedstawia to tablica 2.1. rok 1970, 2.2. - 1971 i 2.3. rok 1972.
Tablica 2.1.Liczba wystąpień w i-tym przedziale przepływów dobowych w roku 1970.
i |
∆ Qi |
wl |
wi |
|||||||||||
|
|
XI |
XII |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
1 |
75,8 - 85,9 |
10 |
2 |
|
|
|
|
|
|
|
|
|
|
12 |
2 |
85,9 - 97,3 |
7 |
4 |
|
|
|
|
|
|
|
|
|
|
11 |
3 |
97,3 - 110,3 |
12 |
15 |
2 |
|
|
|
|
|
|
|
|
1 |
30 |
4 |
110,3 - 125,0 |
|
4 |
4 |
8 |
2 |
|
|
|
|
|
2 |
|
20 |
5 |
125,0 - 141,7 |
1 |
2 |
11 |
8 |
4 |
|
|
|
1 |
|
3 |
3 |
33 |
6 |
141,7 - 160,6 |
|
2 |
8 |
7 |
3 |
|
|
2 |
3 |
|
2 |
6 |
33 |
7 |
160,6 - 181,9 |
|
1 |
2 |
5 |
2 |
|
|
4 |
3 |
|
8 |
6 |
31 |
8 |
181,9 - 206,2 |
|
1 |
3 |
|
3 |
|
7 |
3 |
2 |
|
7 |
9 |
35 |
9 |
206,2 - 233,7 |
|
|
|
|
3 |
|
8 |
2 |
2 |
|
3 |
1 |
19 |
10 |
233,7 - 264,8 |
|
|
1 |
|
1 |
|
3 |
2 |
3 |
|
2 |
4 |
16 |
11 |
264,8 - 300,1 |
|
|
|
|
1 |
|
9 |
3 |
3 |
2 |
3 |
|
21 |
12 |
300,1 - 340,1 |
|
|
|
|
|
9 |
1 |
3 |
1 |
5 |
|
1 |
20 |
13 |
340,1 - 385,4 |
|
|
|
|
|
5 |
1 |
1 |
|
6 |
|
|
13 |
14 |
385,4 - 436,7 |
|
|
|
|
|
4 |
1 |
3 |
|
5 |
|
|
13 |
15 |
436,7 - 494,9 |
|
|
|
|
1 |
4 |
1 |
1 |
1 |
4 |
|
|
12 |
16 |
494,9 - 560,9 |
|
|
|
|
3 |
7 |
|
1 |
|
3 |
|
|
14 |
17 |
560,9 - 635,6 |
|
|
|
|
1 |
1 |
|
|
1 |
1 |
|
|
4 |
18 |
635,6 - 720,3 |
|
|
|
|
3 |
|
|
2 |
|
4 |
|
|
9 |
19 |
720,3 - 816,3 |
|
|
|
|
1 |
|
|
3 |
|
1 |
|
|
5 |
20 |
816,3 - 925,0 |
|
|
|
|
3 |
|
|
|
3 |
|
|
|
6 |
21 |
925,0 - 1048,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
22 |
1048,3 - 1188,0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
23 |
1188,0 - 1346,3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
24 |
1346,3 - 1525,6 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
25 |
1525,6 - 1728,9 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
26 |
1728,9 - 1959,3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
27 |
1959,3 - 2220,4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
28 |
2220,4 - 2516,2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
29 |
2516,2 - 2851,5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
30 |
2851,5 - 3231,5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
31 |
3231,5 - 3662,0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
32 |
3662,0 - 4150,0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
nT=∑ wi |
30 |
31 |
31 |
28 |
31 |
30 |
31 |
30 |
31 |
31 |
30 |
31 |
365 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tablica 2.2.Liczba wystąpień w i-tym przedziale przepływów dobowych w roku 1971.
i |
∆ Qi |
wl |
wi |
|||||||||||
|
|
XI |
XII |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
1 |
75,8 - 85,9 |
|
|
|
|
|
|
|
|
|
8 |
3 |
1 |
12 |
2 |
85,9 - 97,3 |
|
|
|
|
|
|
|
|
|
5 |
11 |
8 |
24 |
3 |
97,3 - 110,3 |
|
|
|
|
|
|
|
|
|
9 |
5 |
8 |
22 |
4 |
110,3 - 125,0 |
|
|
|
|
|
|
|
|
|
4 |
3 |
5 |
12 |
5 |
125,0 - 141,7 |
|
|
4 |
|
|
|
|
|
2 |
1 |
3 |
3 |
13 |
6 |
141,7 - 160,6 |
|
|
3 |
|
|
|
|
|
1 |
1 |
3 |
3 |
11 |
7 |
160,6 - 181,9 |
|
|
8 |
|
1 |
4 |
1 |
2 |
6 |
2 |
1 |
3 |
28 |
8 |
181,9 - 206,2 |
|
5 |
2 |
|
6 |
3 |
5 |
5 |
3 |
1 |
1 |
|
31 |
9 |
206,2 - 233,7 |
2 |
10 |
3 |
5 |
7 |
4 |
6 |
7 |
8 |
|
|
|
52 |
10 |
233,7 - 264,8 |
6 |
3 |
1 |
6 |
1 |
6 |
9 |
6 |
2 |
|
|
|
40 |
11 |
264,8 - 300,1 |
9 |
9 |
3 |
6 |
1 |
4 |
2 |
3 |
2 |
|
|
|
39 |
12 |
300,1 - 340,1 |
5 |
1 |
|
6 |
|
4 |
3 |
4 |
1 |
|
|
|
24 |
13 |
340,1 - 385,4 |
6 |
3 |
4 |
5 |
|
3 |
5 |
2 |
1 |
|
|
|
29 |
14 |
385,4 - 436,7 |
2 |
|
3 |
|
1 |
2 |
|
1 |
1 |
|
|
|
10 |
15 |
436,7 - 494,9 |
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
16 |
494,9 - 560,9 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
17 |
560,9 - 635,6 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
18 |
635,6 - 720,3 |
|
|
|
|
4 |
|
|
|
1 |
|
|
|
5 |
19 |
720,3 - 816,3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
20 |
816,3 - 925,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
21 |
925,0 - 1048,3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
22 |
1048,3 - 1188,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
23 |
1188,0 - 1346,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
24 |
1346,3 - 1525,6 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
25 |
1525,6 - 1728,9 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
26 |
1728,9 - 1959,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
27 |
1959,3 - 2220,4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
28 |
2220,4 - 2516,2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
29 |
2516,2 - 2851,5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
30 |
2851,5 - 3231,5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
31 |
3231,5 - 3662,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
32 |
3662,0 - 4150,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
nT=∑ wi |
30 |
31 |
31 |
28 |
31 |
30 |
31 |
30 |
31 |
31 |
30 |
31 |
365 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tablica 2.3.Liczba wystąpień w i-tym przedziale przepływów dobowych w roku 1972.
i |
∆ Qi |
wl |
wi |
|||||||||||
|
|
XI |
XII |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
1 |
75,8 - 85,9 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
85,9 - 97,3 |
12 |
|
|
|
|
|
|
|
|
|
|
|
12 |
3 |
97,3 - 110,3 |
10 |
|
|
4 |
7 |
1 |
|
3 |
|
|
|
|
25 |
4 |
110,3 - 125,0 |
3 |
1 |
5 |
6 |
5 |
2 |
|
1 |
|
|
|
|
23 |
5 |
125,0 - 141,7 |
1 |
1 |
5 |
3 |
7 |
9 |
|
2 |
|
|
|
|
28 |
6 |
141,7 - 160,6 |
1 |
4 |
7 |
|
5 |
1 |
|
|
2 |
1 |
|
6 |
27 |
7 |
160,6 - 181,9 |
1 |
|
9 |
3 |
3 |
1 |
|
4 |
2 |
5 |
|
7 |
35 |
8 |
181,9 - 206,2 |
2 |
1 |
4 |
9 |
2 |
2 |
2 |
9 |
5 |
2 |
|
8 |
46 |
9 |
206,2 - 233,7 |
|
2 |
|
2 |
1 |
|
5 |
5 |
9 |
2 |
4 |
8 |
38 |
10 |
233,7 - 264,8 |
|
4 |
1 |
2 |
1 |
1 |
4 |
1 |
3 |
1 |
8 |
1 |
27 |
11 |
264,8 - 300,1 |
|
6 |
|
|
|
1 |
4 |
1 |
1 |
2 |
6 |
1 |
22 |
12 |
300,1 - 340,1 |
|
5 |
|
|
|
1 |
3 |
|
|
4 |
6 |
|
19 |
13 |
340,1 - 385,4 |
|
3 |
|
|
|
5 |
3 |
|
3 |
|
3 |
|
17 |
14 |
385,4 - 436,7 |
|
1 |
|
|
|
2 |
4 |
1 |
2 |
2 |
1 |
|
13 |
15 |
436,7 - 494,9 |
|
3 |
|
|
|
4 |
2 |
1 |
4 |
1 |
2 |
|
17 |
16 |
494,9 - 560,9 |
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
6 |
17 |
560,9 - 635,6 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
18 |
635,6 - 720,3 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
19 |
720,3 - 816,3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
20 |
816,3 - 925,0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
21 |
925,0 - 1048,3 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
2 |
22 |
1048,3 - 1188,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
23 |
1188,0 - 1346,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
24 |
1346,3 - 1525,6 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
25 |
1525,6 - 1728,9 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
26 |
1728,9 - 1959,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
27 |
1959,3 - 2220,4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
28 |
2220,4 - 2516,2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
29 |
2516,2 - 2851,5 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
30 |
2851,5 - 3231,5 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
31 |
3231,5 - 3662,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
32 |
3662,0 - 4150,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
nT=∑ wi |
30 |
31 |
31 |
29 |
31 |
30 |
31 |
30 |
31 |
31 |
30 |
31 |
366 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sporządziliśmy następnie tablicę zbiorczą dla wszystkich N lat.
Tablica 2.4.Częstości sumy czasów trwania i gęstości częstości przepływów dobowych w okresie 1970-72
i |
∆ Qi |
wi |
wj |
wj |
ti |
gi |
||
|
|
1970 |
1971 |
1972 |
|
|
|
|
1 |
75,8 - 85,9 |
12 |
12 |
0 |
24 |
8,00 |
365,33 |
0,79208 |
2 |
85,9 - 97,3 |
11 |
24 |
12 |
47 |
15,67 |
357,33 |
1,37427 |
3 |
97,3 - 110,3 |
30 |
22 |
25 |
77 |
25,67 |
341,67 |
1,97436 |
4 |
110,3 - 125,0 |
20 |
12 |
23 |
55 |
18,33 |
316,00 |
1,24717 |
5 |
125,0 - 141,7 |
33 |
13 |
28 |
74 |
24,67 |
297,67 |
1,47705 |
6 |
141,7 - 160,6 |
33 |
11 |
27 |
71 |
23,67 |
273,00 |
1,25220 |
7 |
160,6 - 181,9 |
31 |
28 |
35 |
94 |
31,33 |
249,33 |
1,46417 |
8 |
181,9 - 206,2 |
35 |
31 |
46 |
112 |
37,33 |
218,00 |
1,54270 |
9 |
206,2 - 233,7 |
19 |
52 |
38 |
109 |
36,33 |
180,67 |
1,32121 |
10 |
233,7 - 264,8 |
16 |
40 |
27 |
83 |
27,67 |
144,33 |
0,88960 |
11 |
264,8 - 300,1 |
21 |
39 |
22 |
82 |
27,33 |
116,67 |
0,77432 |
12 |
300,1 - 340,1 |
20 |
24 |
19 |
63 |
21,00 |
89,33 |
0,52500 |
13 |
340,1 - 385,4 |
13 |
29 |
17 |
59 |
19,67 |
68,33 |
0,43414 |
14 |
385,4 - 436,7 |
13 |
10 |
13 |
36 |
12,00 |
48,67 |
0,23346 |
15 |
436,7 - 494,9 |
12 |
4 |
17 |
33 |
11,00 |
36,67 |
0,18900 |
16 |
494,9 - 560,9 |
14 |
3 |
6 |
23 |
7,67 |
25,67 |
0,11634 |
17 |
560,9 - 635,6 |
4 |
3 |
0 |
7 |
2,33 |
18,00 |
0,03124 |
18 |
635,6 - 720,3 |
9 |
5 |
3 |
17 |
5,67 |
15,67 |
0,06690 |
19 |
720,3 - 816,3 |
5 |
1 |
1 |
7 |
2,33 |
10,00 |
0,02431 |
20 |
816,3 - 925,0 |
6 |
0 |
1 |
7 |
2,33 |
7,67 |
0,02145 |
21 |
925,0 - 1048,3 |
0 |
2 |
2 |
4 |
1,33 |
5,33 |
0,01081 |
22 |
1048,3 - 1188,0 |
1 |
0 |
0 |
1 |
0,33 |
4,00 |
0,00239 |
23 |
1188,0 - 1346,3 |
2 |
0 |
0 |
2 |
0,67 |
3,67 |
0,00421 |
24 |
1346,3 - 1525,6 |
0 |
0 |
0 |
0 |
0,00 |
3,00 |
0,00000 |
25 |
1525,6 - 1728,9 |
0 |
0 |
1 |
1 |
0,33 |
3,00 |
0,00164 |
26 |
1728,9 - 1959,3 |
1 |
0 |
0 |
1 |
0,33 |
2,67 |
0,00145 |
27 |
1959,3 - 2220,4 |
0 |
0 |
0 |
0 |
0,00 |
2,33 |
0,00000 |
28 |
2220,4 - 2516,2 |
1 |
0 |
1 |
2 |
0,67 |
2,33 |
0,00225 |
29 |
2516,2 - 2851,5 |
0 |
0 |
1 |
1 |
0,33 |
1,67 |
0,00099 |
30 |
2851,5 - 3231,5 |
0 |
0 |
1 |
1 |
0,33 |
1,33 |
0,00088 |
31 |
3231,5 - 3662,0 |
1 |
0 |
0 |
1 |
0,33 |
1,00 |
0,00077 |
32 |
3662,0 - 4150,0 |
2 |
0 |
0 |
2 |
0,67 |
0,67 |
0,00137 |
Suma |
365 |
365 |
366 |
1096 |
365,33 |
|
|
|
|
|
|
|
|
|
|
|
|
* * *
3. Analiza niejednorodności ciągów pomiarowych.
Jednorodność cięgów pomiarowych jest podstawą do tego, aby wyniki uzyskane z obliczeń były poprawne.
Przez pojęcie jednorodności rozumie się to że, zbiór czynników wywołujących dane zjawisko jest taki sam ze względu na takie czynniki jak: zastosowane przyrządy, czas pomiaru itp.
Niejednorodność ciągów pomiarowych dzieli się na niejednorodność genetyczną, która jest możliwa do zidentyfikowania, oraz na niejednorodność statystyczną, wywołaną przez czynniki których nie można określić i wyodrębnić, a które wpływają na zmianę własności statystycznych ciągów pomiarowych.
Naszą analizę niejednorodności przeprowadzamy na ciągu pomiarowym stanowiącym wartości maksymalne przepływów z obu półroczy lat 1961-1990.
Omawiane niżej wykresy znajdują się na końcu tego rozdziału.
Na początku badań należy wykryć niejednorodność genetyczną, przy czym wyróżnia się trzy rodzaje tej niejednorodności:
niejednorodność aprioryczną wykrywamy poprzez analizę genezy badanego zjawiska, (przepływów maksymalnych).
Przepływy maksymalne mogą być generowane przez dwa mechanizmy: roztopy i deszcze ,a zbiór czynników wywołujących powstawanie tych zjawisk jest inny. Określając genezę wezbrań dzielimy Qmax na Qmax,roztopowe i Qmax,deszczowe tworząc w ten sposób dwa ciągi jednorodne apriorycznie (Qmax,r z lat 1961-1990 przedstawia wykres 3.1 , a Qmax,d z lat 1961-1990 wykres 3.2);
jednorodność czasowa uwarunkowana jest niezmiennością w czasie zbioru czynników wywołujących badane zjawisko - jest to najczęściej występujący rodzaj niejednorodności;
niejednorodność pomiarowa wynika z niejednorodności warunków przeprowadzania pomiarów.
W naszym projekcie niejednorodność pomiarową i czasową traktujemy jako czynniki niezidentyfikowane.
Po analizie niejednorodności genetycznej badania niejednorodności przeprowadzamy metodami statystycznymi stosując odpowiednie testy weryfikujące.
Analiza niejednorodności statystycznej:
Wykrywanie elementów odstających badanej zmiennej losowej
Wystąpienie elementów odstających może być spowodowane przyczynami naturalnymi (wtedy nie odrzucamy takich elementów), bądź błędem w obliczeniach - wtedy wykonujemy korektę błędów. Wykrywanie elementów odstających przeprowadzamy testem Grubbsa-Becka (dla Qmax,r wykres 3.3 , dla Qmax,d wykres 3.4).
Sprawdzenie niezależności badanej zmiennej losowej
Zmienne losowe niezależne tworzą próbę prostą. Badanie niezależności wykonujemy testem serii. Sprawdzamy wewnętrzną korelację zmiennej losowej testem współczynnika autokorelacji (dla Qmax,r wykres 3.5, dla Qmax,d wykres 3.6). W przypadku, gdy badana zmienna nie jest niezależna, należy przeprowadzić analizę czynników wpływających na przebieg realizacji badanej zmiennej oraz sprawdzenie danych pod kątem wystąpienia błędów na drodze od pomiaru do bazy danych.
Sprawdzenie stacjonarności badanej zmiennej
Do badania stacjonarności wykonujemy trzy testy:
test sumy rang - wykrywa skokową zmianę przepływów w ciągu pomiarowym,
test na trend wartości średniej,
test na trend wariancji.
W przypadku gdy zmienna losowa nie jest stacjonarna należy przeprowadzić podobną analizę jak przy badaniu niezależności.
Gdy badana zmienna jest niezależna i stacjonarna to badany ciąg pomiarowy jest jednorodny.
Analizę w niejednorodności wykonujemy za pomocą programu ANJ na poziomie istotności , a wyniki naszej analizy przedstawia raport, który jest w załączniku na końcu projektu.
Z raportu, na podstawie wyżej wymienionych założeń, wynika ,że badany przez nas ciąg pomiarowy jest ciągiem jednorodnym - dla całego roku hydrologicznego ciąg pomiarowy jest niezależny i stacjonarny.
* * *
4. Rozkład prawdopodobieństwa przewyższenia przepływów maksymalnych rocznych.
Aby można było przystąpić do ustalenia rozkładu prawdopodobieństw przewyższenia przepływów maksymalnych badana próba musi być jednorodna. Założenie to jest w przypadku naszych danych spełnione (rozdz. 3).
Najpierw ustalamy dwa rozkłady dla ciągu Qmax , r i Qmax,d :
na podstawie obserwacji próby losowej oraz ograniczeń fizycznych badanego zjawiska, czyli przepływów maksymalnych, można wyróżnić cztery rozkłady, które najlepiej opisują przepływy maksymalne:
rozkład gamma (Pearsona III typ );
rozkład log-normalny;
rozkład Weibulla;
rozkład log-gamma ( log - Pearsona III typ).
Metodą największej wiarygodności przeprowadzamy estymację parametrów
tych rozkładów.
Sprawdzamy następnie zgodność rozkładu teoretycznego z empirycznym, wykonując
test ![]()
na poziomie istotności , Weryfikujemy hipotezę o zgodności rozkładu teoretycznego z empirycznym.
Gdy po wykonaniu testu hipotezy nie odrzucamy, to oznacza , że badany rozkład jest niesprzeczny na danym poziomie istotności.
Wybór dla poszczególnych typów rozkładów funkcji, która najlepiej dopasuje się do rozkładu empirycznego, wykonuje się za pomocą kryterium odległości Kołmogorowa D![]()
:
D![]()
=![]()
Spośród funkcji w obrębie jednego rozkładu wybieramy tą, która ma najmniejszą wartość D![]()
. Uzyskujemy w ten sposób po jednej funkcji dla każdego z czterech rozkładów, które najlepiej opisują rozkład empiryczny.
Wybór jednej najbardziej wiarygodnej funkcji rozkładu przepływów maksymalnych spośród czterech wykonuje się za pomocą kryterium Akaike:
AIC=K![]()
=2L-2![]()
Po wykonaniu tej procedury otrzymujemy dwie krzywe. Jedna najlepiej opisuje przepływy maksymalne roztopowe, a druga przepływy maksymalne deszczowe.
Następnie konstruujemy krzywą funkcji prawdopodobieństwa przewyższenia przepływów maksymalnych rocznych jako prawdopodobieństwo alternatywy nie wykluczających się zdarzeń niezależnych:
P(Qmax)r = P(Qmax,roz.) + P(Qmax, d) -P(qmax,roz.)*P(Qmax,d)
Błędy liczymy ustalając górną granicę przedziału ufności na poziomie P![]()
=84% :
Z![]()
Sprawdzenie warunku dostatecznej liczebności próby losowej wykonuje się za pomocą:
S(Z![]()
/Z![]()
![]()
0,2
Gdy ten błąd będzie mniejszy lub równy 20% to oznacza, że kwantyle są obliczone bezbłędnie, gdy błąd będzie większy niż 20% to powstaje niepewność związana z długością próby.
Ustalanie rozkładu prawdopodobieństwa przewyższenia przepływów maksymalnych rocznych wykonujemy za pomocą programu QMAX, a uzyskane wyniki przedstawia załączony raport na końcu projektu.
Z raportu wynika, że rozkładem który najlepiej opisuje przepływy maksymalne roczne roztopowe jest rozkład Weibulla, z następującymi wartościami parametrów:
d = 340,000
,
= 1,474
Najbardziej wiarygodnym rozkładem dla przepływów maksymalnych rocznych deszczowych jest także rozkład Weibulla, o następujących wartościach parametrów:
d = 249,000
,
= 1,197
* * *
5. Przepływy minimalne o określonym prawdopodobieństwie przekroczenia.
Próbę losową do wyznaczenia przepływów minimalnych o określonym prawdopodobieństwie przekroczenia stanowią minimalne przepływy z półrocza letniego Qmin,l.
Na podstawie obserwacji próby losowej i zakresu ograniczeń badanego zjawiska, można wnioskować iż rozkładem teoretycznym, który najlepiej opisuje przepływy minimalne, jest rozkład Fishera-Tippeta typu III.
Konstruujemy rosnący ciąg przepływów minimalnych z półrocza letniego i dla każdego elementu tego ciągu określamy prawdopodobieństwo empiryczne i teoretyczne wystąpienia Qmin,l.
Pm,N - prawdopodobieństwo empiryczne obliczamy ze wzoru:
Pm,N = (m / N+1) *100%
Pm - prawdopodobieństwo teoretyczne odczytujemy z wykresu 1.
Wyniki przedstawia tab.1
2) Metodą momentów statystycznych estymujemy parametry rozkładu Fishera-Tippetta typu III, którymi są: ![]()
, k ≥0 .
Musimy estymować trzy parametry więc tworzymy trzy równania. W pierwszym porównujemy średnie arytmetyczne obliczone z próby losowej i z rozkładu teoretycznego, w drugim równaniu porównujemy odchylenia standardowe.
Zamiast liczyć trzeci moment wyznaczamy parametr pomocniczy:
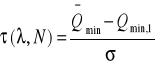
gdzie:
![]()
- średnia wartość z Qmin,l
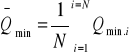
= 93,53
Qmin,1 - pierwszy element z próby (najmniejsza wartość przepływu)
Qmin,1= 57,00
W przypadku kilku takich samych Qmin trzeba zmienić liczebność próby :
N'= N/n.
W naszym projekcie n=1 , więc N'=N.
![]()
- odchylenie standardowe
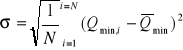
= 19,955
Mając obliczony τ =1,833 i N=30 odczytujemy z tablicy I λ=0,35.
3) Wyznaczamy poszukiwane parametry.
k = 1/λ = 2,857
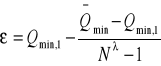
= 45,9
ε > 0 , więc:
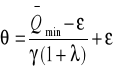
= 99,35
gdzie: ![]()
= 0,89115
Wyznaczamy Qmin,p:
Qmin,p=![]()
gdzie: Yp=ln[ -ln(1-p)]
Tablica 5.1.
p |
yp |
Qmin,p |
0,99 |
1,52718 |
137,1187 |
0,95 |
1,097189 |
124,3736 |
0,9 |
0,834032 |
117,4687 |
0,8 |
0,475885 |
109,037 |
0,7 |
0,185627 |
102,9379 |
0,6 |
-0,08742 |
97,73933 |
0,5 |
-0,36651 |
92,91502 |
0,4 |
-0,67173 |
88,1516 |
0,3 |
-1,03093 |
83,16002 |
0,2 |
-1,49994 |
77,5193 |
0,1 |
-2,25037 |
70,2156 |
0,05 |
-2,9702 |
64,80031 |
0,01 |
-4,60015 |
56,58343 |
Załączony jest na końcu projektu wykres (wykres 5.1.) przedstawiający prawdopodobieństwo teoretyczne Pm.
Tablica 5.2. Prawdopodobieństwo empiryczne i teoretyczne.
Lp |
Qmin,l |
Pm,n |
Pm |
1 |
57 |
3,225806 |
1,05 |
2 |
63,6 |
6,451613 |
4 |
3 |
68,2 |
9,677419 |
7,6 |
4 |
70,5 |
12,90323 |
9,8 |
5 |
73,6 |
16,12903 |
13 |
6 |
77,4 |
19,35484 |
19 |
7 |
78 |
22,58065 |
21 |
8 |
78,4 |
25,80645 |
21,5 |
9 |
79,6 |
29,03226 |
23,8 |
10 |
79,6 |
32,25806 |
23,8 |
11 |
83 |
35,48387 |
30 |
12 |
83,6 |
38,70968 |
31 |
13 |
83,6 |
41,93548 |
31 |
14 |
86,4 |
45,16129 |
36 |
15 |
89,4 |
48,3871 |
42 |
16 |
92,4 |
51,6129 |
49 |
17 |
97,8 |
54,83871 |
60 |
18 |
97,8 |
58,06452 |
60 |
19 |
102 |
61,29032 |
68 |
20 |
102 |
64,51613 |
68 |
21 |
104 |
67,74194 |
72 |
22 |
106 |
70,96774 |
75 |
23 |
107 |
74,19355 |
77 |
24 |
110 |
77,41935 |
82 |
25 |
112 |
80,64516 |
84 |
26 |
113 |
83,87097 |
85 |
27 |
120 |
87,09677 |
91,5 |
28 |
121 |
90,32258 |
93 |
29 |
124 |
93,54839 |
95 |
30 |
145 |
96,77419 |
99,5 |
Sprawdzenie zgodności rozkładu teoretycznego z rozkładem empirycznym za pomocą testu ![]()
Pearsona.
Założenia:
parametry rozkładu estymowane są metodą największej wiarygodności (co w naszym przypadku nie jest spełnione), długi ciąg pomiarowy - co najmniej 5 obserwacji w każdym przedziale (ponieważ N=30 to stworzyliśmy sześć przedziałów po pięć elementów).
W teście tym weryfikujemy hipotezę Ho:
rozkład teoretyczny jest zgodny z rozkładem empirycznym,
za pomocą statystyki:
![]()
,
gdzie:
r - liczba przedziałów
ni - liczebność empiryczna przedziałów i=1,......r
πi- prawdopodobieństwo wpadnięcia zmiennej losowej ( Qmin,j) do j-tego przedziału j=1,....N
Nπi - liczebność teoretyczna przedziałów
Wartość krytyczną statystyki ![]()
określa się z tablic w zależności od przyjętego poziomu istotności α=0,05 i liczby stopni swobody ss = r-k-1=6-3-1=2
![]()
= 5,991
- jeśli ![]()
<![]()
to nie ma podstaw do odrzucenia hipotezy H0
- jeśli ![]()
![]()
![]()
to hipotezę Ho odrzucamy
Tablica 5.3. Obliczenia ![]()
.
i |
Qmin |
ni |
gamma |
P(gamma) |
Pii |
N*Pii |
ni-N*Pii |
(ni-Npii)^2 |
całe |
|
57 |
|
|
|
|
|
|
|
|
|
63,6 |
|
|
|
|
|
|
|
|
1 |
68,2 |
5 |
75,5 |
0,17 |
0,17 |
5,1 |
-0,1 |
0,01 |
0,0019608 |
|
70,5 |
|
|
|
|
|
|
|
|
|
73,6 |
|
|
|
|
|
|
|
|
|
77,4 |
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
2 |
78,4 |
5 |
81,3 |
0,27 |
0,1 |
3 |
2 |
4 |
1,3333333 |
|
79,6 |
|
|
|
|
|
|
|
|
|
79,6 |
|
|
|
|
|
|
|
|
|
83 |
|
|
|
|
|
|
|
|
|
83,6 |
|
|
|
|
|
|
|
|
3 |
83,6 |
5 |
90,9 |
0,46 |
0,19 |
5,7 |
-0,7 |
0,49 |
0,0859649 |
|
86,4 |
|
|
|
|
|
|
|
|
|
89,4 |
|
|
|
|
|
|
|
|
|
92,4 |
|
|
|
|
|
|
|
|
|
97,8 |
|
|
|
|
|
|
|
|
4 |
97,8 |
5 |
103 |
0,7 |
0,24 |
7,2 |
-2,2 |
4,84 |
0,6722222 |
|
102 |
|
|
|
|
|
|
|
|
|
102 |
|
|
|
|
|
|
|
|
|
104 |
|
|
|
|
|
|
|
|
|
106 |
|
|
|
|
|
|
|
|
5 |
107 |
5 |
112,5 |
0,85 |
0,15 |
4,5 |
0,5 |
0,25 |
0,0555556 |
|
110 |
|
|
|
|
|
|
|
|
|
112 |
|
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
6 |
121 |
5 |
_ |
_ |
0,15 |
4,5 |
0,5 |
0,25 |
0,0555556 |
|
124 |
|
|
|
|
|
|
|
|
|
145 |
|
|
|
|
|
|
|
|
SUMA: |
30 |
|
|
1 |
|
|
|
2,147076 |
|
![]()
=2,14 < ![]()
więc na danym poziomie istotności ( = 0,05) nie ma podstaw do odrzucenia hipotezy H0 , co oznacza że rozkład teoretyczny Fishera-Tippetta jest rozkładem zgodnym z rozkładem empirycznym.
* * *
6. Przepływy konwencjonalne
Są to przepływy ustalane według potrzeb związanych z wykorzystaniem i ochroną zasobów wodnych, a także zapobiegania przed negatywnym działaniem wód. Do najbardziej powszechnych rodzajów przepływów tego rodzaju należą:
Przepływ żeglugowy
Przepływ dozwolony
Przepływ nienaruszalny
Przepływ brzegotwórczy
a) Przepływ żeglugowy
W tym przypadku mamy do czynienia z najwyższym przepływem żeglugowym Qmax,ż oraz z najniższym przepływem żeglugowym Qmin,ż.
Najwyższy przepływ żeglugowy nazywa się przepływ odpowiadający takiemu stanowi wody, powyżej którego żegluga nie powinna się odbywać.
Przepływ ten obecnie przyjmowany jest jako przepływ maksymalny roczny o określonym prawdopodobieństwie występowania. Wg Orlewicza powinien odpowiadać Qmax,60%.
Stan wody odpowiadający Qmax,ż określa się jako stan wynikający z różnicy między rzędną spodu konstrukcji a gabarytem wysokościowym największych statków eksploatowanych na drodze wodnej.
Najniższy przepływ żeglowny nazywamy przepływ poniżej którego nie powinna odbywać się żegluga. Przepływ ten ustalany jest według wymaganych głębokości i szerokości na drodze wodnej.
Qmax,60%. = 1169 [m3/s]
b) Przepływ dozwolony i dopuszczalny
Przepływ dozwolony Qdoz. jest to największy przepływ podczas którego nie obserwujemy szkód powodziowych. W przypadku braku danych dotyczących powodzi lub zagrożenia powodziowego przyjmujemy Qdoz. jako średnią arytmetyczną z przepływów maksymalnych rocznych SWQ.
Przepływem dopuszczalnym Qdop. jest przepływ przy którym dopuszcza się wystąpienia niewielkich szkód powodziowych. Sytuacja taka ma miejsce w przypadku zagrożenia wysokim wezbraniem, stąd konieczność opróżnienia zbiornika na przyjęcie fali powodziowej.
Wielkość Qdop. przyjmowana jest w zależności od poziomu zagrożenia i innych czynników. Jeżeli nie mamy takich danych przyjmujemy w przybliżeniu za Qdop. poziom przepływu maksymalnego o prawdopodobieństwie przewyższenia 40% lub 30%.
dozwolony Qmax,50%. = 1336,2 [m3/s]
dopuszczalny Qmax,40%. = 1535,4 [m3/s]
Przepływ nienaruszalny
Przepływ nienaruszalny Qn jest graniczną wartością przepływu rzecznego, poniżej której przepływy wody w rzekach nie powinny być zmniejszane na skutek działalności gospodarczej. Przepływy te ustalane są w poszczególnych przekrojach rzeki z różnych względów tj. ochrony środowiska, wymagania społeczne na cele rekreacyjne. Do określenia wielkości przepływu nienaruszalnego (wody odpowiadające jakościowo pierwszej i drugiej klasy) potrzebne są kryteria:
wymagania rybacko-wędkarskie (Qnr)
ochrona obiektów przyrodniczych (parki narodowe i rezerwaty) (Qnop) przesłanki hydrobiologiczne warunkujące zachowanie form flory i fauny (Qnh) wymagania rzecznej turystyki wodnej (Qnt).
Do określenia parametru Qn wymagane jest indywidualne rozpoznanie danego cieku i jego odcinków w celu określenia, które z podanych wyżej kryteriów należy brać pod uwagę w celu wyznaczenia Qn. Musimy brać pod uwagę sezonową zmienność kryteriów. Jeżeli w danym przekroju rzeki do wyznaczenia Qn posługujemy się więcej niż jednym kryterium, wartość miarodajną przepływu nienaruszalnego określa kryterium, dla którego przepływ ten jest największy, czyli Qn = max(Qnh, Qnr, Qnop, Qnt)
Określenie przepływu nienaruszalnego Qnh (patrząc na prawidłowy rozwój gatunków fauny i flory) jest trudne. Dla rzek, na których prowadzone są pomiary hydrometryczne przepływ ten ustala się tak aby dno koryta będące naturalnym siedliskiem życia biologicznego w rzece nie ulegało zmianie. Wartość prędkości nie dopuszczającej do zmian morfologicznych koryta powinna zawierać się pomiędzy górną granicą (nie rozmywającą koryta), a dolną granicą (nie zamulającą). W przypadku braku pomiarów wielkość przepływu Qnh = kSNQ , jednak Qnh > NNQ
Wartość współczynnika k dla dużych rodzajów rzek o wielkości zlewni powyżej 2500 km2 wynosi 0,5, dla małych rzek nizinnych wartość 1,0, dla przejściowych i podgórskich 1,27, a dla górskich 1,52.
Kryterium rybacko-wędkarskie uwzględnia podział rzek na :rzeki ryb łososiowatych i rzek ryb nizinnych, oraz na trzy fazy rozwoju ryb: faza wędrówek tarłowych i rozrodu (marzec-kwiecień, wrzesień-listopad dla ryb łososiowatych; marzec-czerwiec dla ryb nizinnych), faza wzrostu (maj-sierpień dla ryb łososiowatych; lipiec-listopad dla ryb nizinnych) oraz fazę przezimowania (grudzień-luty). Jako przepływ Qnr przyjmuje się, dla poszczególnych faz, wartości odpowiadające SNQ, które są określane oddzielnie dla poszczególnych okresów.
Przepływy nienaruszalne dotyczące ochrony przyrody Qnop są zazwyczaj wyższe od Qnh. Przy ustaleniu tego przepływu uwzględnia się ochronę przed przesuszaniem terenów powstałym w skutek długotrwałego wyczerpania zasobów wodnych rzek
Przepływ nienaruszalny ze względu na wymogi turystyki Qnt określany jest ze względu na wymagane głębokości na szlakach turystki kajakowej (30-25 cm) i szlakach żeglarskich (125-105cm lub 65-50 cm). Wartości Qnt odpowiadają mniej więcej wartości Qnh, a dla żeglarstwa są dużo większe.
Qn = 84,8 [m3/s]
Przepływ brzegotwórczy
Przepływ brzegotwórczy Qbt (przepływ korytotwórczy) jest przepływem najsilniej wpływającym na formowanie się koryta rzecznego.
Procesy brzegotwórcze zależą od siły transportu rumowiska rzecznego i od czasu działania tej siły. W celu określenia Qbt musimy potrzebna jest znajomość zależności pomiędzy wielkością przepływu a wielkością transportu rumowiska rzecznego G = f(Q) oraz zależności określającej czas trwania poszczególnych wartości przepływów (krzywa gęstości częstości przepływów g = f(Q). Krzywa gG dla poszczególnych wartości Q pozwala określić Qbt jako przepływ odpowiadający maksymalnemu iloczynowi gG. Krzywa iloczynów gG może być zastąpiona przez krzywą iloczynów gQ. Wartość maksymalna gQ określa przepływ brzegotwórczy .
Qbt = 299,36
Wykres 6.1. Uproszczony sposób wyznaczania przepływu brzegotwórczego.
* * *
Załącznik do pkt.1
a)
Dane opisujące natężenie przepływów [m3/s] w 1961 roku
Dzień |
Miesiące |
|||||||||||
|
XI |
XII |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
136,0 |
163,0 |
185,0 |
161,0 |
187,0 |
305,0 |
115,0 |
226,0 |
279,0 |
396,0 |
82,1 |
85,0 |
2 |
138,0 |
151,0 |
144,0 |
185,0 |
200,0 |
455,0 |
97,8 |
153,0 |
208,0 |
384,0 |
85,0 |
73,4 |
3 |
124,0 |
147,0 |
142,0 |
192,0 |
226,0 |
435,0 |
118,0 |
148,0 |
142,0 |
350,0 |
82,1 |
69,3 |
4 |
126,0 |
140,0 |
148,0 |
240,0 |
263,0 |
382,0 |
113,0 |
142,0 |
125,0 |
292,0 |
80,6 |
60,1 |
5 |
126,0 |
134,0 |
157,0 |
191,0 |
263,0 |
425,0 |
115,0 |
135,0 |
146,0 |
290,0 |
76,3 |
59,0 |
6 |
126,0 |
134,0 |
181,0 |
149,0 |
226,0 |
370,0 |
144,0 |
149,0 |
155,0 |
254,0 |
77,7 |
65,9 |
7 |
126,0 |
151,0 |
242,0 |
139,0 |
236,0 |
377,0 |
125,0 |
189,0 |
139,0 |
191,0 |
79,2 |
63,6 |
8 |
133,0 |
159,0 |
220,0 |
132,0 |
214,0 |
345,0 |
140,0 |
258,0 |
123,0 |
161,0 |
76,3 |
59,0 |
9 |
133,0 |
144,0 |
183,0 |
126,0 |
222,0 |
286,0 |
146,0 |
279,0 |
109,0 |
146,0 |
93,0 |
62,4 |
10 |
151,0 |
144,0 |
180,0 |
132,0 |
230,0 |
260,0 |
162,0 |
279,0 |
104,0 |
133,0 |
93,0 |
57,0 |
11 |
111,0 |
170,0 |
187,0 |
176,0 |
248,0 |
234,0 |
206,0 |
271,0 |
99,4 |
128,0 |
101,0 |
63,6 |
12 |
161,0 |
174,0 |
218,0 |
292,0 |
228,0 |
208,0 |
202,0 |
230,0 |
97,8 |
176,0 |
82,1 |
61,3 |
13 |
119,0 |
290,0 |
200,0 |
284,0 |
226,0 |
202,0 |
185,0 |
299,0 |
103,0 |
146,0 |
85,0 |
64,7 |
14 |
124,0 |
288,0 |
210,0 |
281,0 |
218,0 |
214,0 |
229,0 |
345,0 |
103,0 |
146,0 |
82,1 |
64,7 |
15 |
127,0 |
283,0 |
180,0 |
267,0 |
222,0 |
197,0 |
187,0 |
392,0 |
91,4 |
392,0 |
83,5 |
69,3 |
16 |
244,0 |
375,0 |
168,0 |
260,0 |
310,0 |
172,0 |
168,0 |
354,0 |
101,0 |
327,0 |
83,5 |
73,4 |
17 |
189,0 |
337,0 |
142,0 |
254,0 |
345,0 |
158,0 |
161,0 |
347,0 |
89,0 |
256,0 |
77,7 |
69,3 |
18 |
206,0 |
335,0 |
106,0 |
252,0 |
336,0 |
149,0 |
189,0 |
286,0 |
79,2 |
230,0 |
74,8 |
62,4 |
19 |
227,0 |
299,0 |
90,0 |
256,0 |
294,0 |
142,0 |
178,0 |
181,0 |
111,0 |
183,0 |
76,3 |
67,1 |
20 |
199,0 |
290,0 |
111,0 |
265,0 |
279,0 |
140,0 |
181,0 |
155,0 |
91,4 |
155,0 |
70,5 |
76,3 |
21 |
180,0 |
343,0 |
126,0 |
279,0 |
271,0 |
130,0 |
168,0 |
187,0 |
82,1 |
146,0 |
76,3 |
71,9 |
22 |
182,0 |
301,0 |
112,0 |
332,0 |
226,0 |
135,0 |
168,0 |
142,0 |
125,0 |
142,0 |
68,2 |
67,1 |
23 |
203,0 |
292,0 |
104,0 |
296,0 |
256,0 |
125,0 |
172,0 |
132,0 |
116,0 |
125,0 |
67,1 |
63,6 |
24 |
189,0 |
297,0 |
106,0 |
284,0 |
214,0 |
120,0 |
157,0 |
125,0 |
106,0 |
121,0 |
71,9 |
62,4 |
25 |
193,0 |
244,0 |
109,0 |
263,0 |
265,0 |
123,0 |
168,0 |
118,0 |
118,0 |
115,0 |
67,1 |
58,0 |
26 |
203,0 |
193,0 |
81,0 |
242,0 |
248,0 |
116,0 |
200,0 |
115,0 |
96,2 |
113,0 |
64,7 |
65,9 |
27 |
182,0 |
185,0 |
125,0 |
218,0 |
216,0 |
115,0 |
151,0 |
108,0 |
96,2 |
125,0 |
69,3 |
57,0 |
28 |
174,0 |
164,0 |
127,0 |
195,0 |
208,0 |
113,0 |
139,0 |
108,0 |
82,1 |
113,0 |
68,2 |
64,7 |
29 |
155,0 |
147,0 |
135,0 |
- |
267,0 |
118,0 |
139,0 |
118,0 |
88,2 |
101,0 |
68,2 |
73,4 |
30 |
144,0 |
183,0 |
140,0 |
- |
286,0 |
118,0 |
146,0 |
189,0 |
85,0 |
97,8 |
64,7 |
63,6 |
31 |
- |
178,0 |
150,0 |
- |
281,0 |
- |
172,0 |
- |
101,0 |
111,0 |
- |
59,0 |
b)
Dane opisujące przepływy główne I rzędu z lat 1961-90
Rok |
WQ |
SQ |
NQ |
|
|
|
|
1961 |
455,0 |
170,4 |
57,0 |
1962 |
3000,0 |
323,5 |
68,2 |
1963 |
1140,0 |
195,4 |
68,2 |
1964 |
1310,0 |
164,4 |
58,0 |
1965 |
2140,0 |
295,6 |
77,7 |
1966 |
2000,0 |
289,1 |
88,2 |
1967 |
1070,0 |
280,9 |
83,6 |
1968 |
1710,0 |
263,6 |
90,6 |
1969 |
763,0 |
184,3 |
73,6 |
1970 |
4150,0 |
298,1 |
75,8 |
1971 |
996,0 |
238,0 |
78,0 |
1972 |
3200,0 |
257,9 |
89,2 |
1973 |
2270,0 |
215,9 |
78,4 |
1974 |
1990,0 |
280,6 |
88,6 |
1975 |
1660,0 |
343,9 |
124,0 |
1976 |
844,0 |
252,0 |
102,0 |
1977 |
1230,0 |
272,0 |
102,0 |
1978 |
875,0 |
239,9 |
87,2 |
1979 |
895,0 |
252,1 |
104,0 |
1980 |
2430,0 |
290,1 |
101,0 |
1981 |
1300,0 |
244,1 |
121,0 |
1982 |
916,0 |
217,3 |
86,4 |
1983 |
1810,0 |
219,2 |
77,4 |
1984 |
649,0 |
145,0 |
83,0 |
1985 |
2170,0 |
250,4 |
78,0 |
1986 |
795,0 |
194,4 |
79,6 |
1987 |
2790,0 |
200,5 |
72,1 |
1988 |
821,0 |
192,2 |
81,8 |
1989 |
1590,0 |
214,8 |
87,0 |
1990 |
554,0 |
161,4 |
83,6 |
Załącznik do pkt. 3
raport z programu ANJ
Załącznik do pkt. 4
raport z programu QMAX
Załącznik do pkt. 5
wykres prawdopodobieństwa Pm
Wyszukiwarka