LITERATURA:

1. H.R. VARIAN "Mikroekonomia" podtytuł: "Kurs średniej…" PWN

2. A.C. CHIANG "Podstawy ekonomii matematycznej"

3. E. PANEK "Ekonomia matematyczna" AE Poznań

4. A. MALAWSKI "Wprowadzenie do Ekonomii matematycznej" AE Kraków

WYKŁAD I 20.09.2003 r.

Temat: Funkcje wiążące zmienne ekonomiczne

PODSTAWOWE POJĘCIA W EKONOMII

EKONOMIA- gospodarka, tzn. Sposób w jaki społeczeństwo gospodarujące (uczestnicy ekonomii) "gospodaruje", tzn.: wytwarza, dzieli i spożywa towary.

EKONOMIA (Economics) - nauka o gospodarce, czyli o ekonomii.

Podstawowe zjawiska badane w Ekonomii:

• produkcja (wytwarzanie)

• dystrybucja (podział)

• konsumpcja (spożycie)

UCZESTNICY EKONOMII- [AGENCI]- konsumenci i producenci

TOWARY- dobra i usługi

CEL EKONOMII - wyjaśnić funkcjonowanie gospodarki. WIELKI CEL: odkrycie
i uzasadnienie praw ekonomicznych, czyli stwierdzeń dotyczących tendencji ekonomicznych

EKONOMIA:

1. TWORZY TEORIE, które mają wyjaśnić funkcjonowanie gospodarki a następnie stara się je

2. ZWERYFIKOWAĆ poprzez odniesienia ich do wydarzeń i danych realnego świata

EKONOMIA jest więc dyscypliną empiryczną, bo choć wyklucza przeprowadzanie eksperymentów, to pragnie wiązać teorię z realnym światem.

AD. 1:

TEORIA EKONOMICZNA- inaczej model ekonomiczny, formalny schemat przedstawiający w pewien sposób podstawowe cechy rozpatrywanego fragmentu rzeczywistości (tu: ekonomicznej)

MODELE EKONOMICZNE- mają wyjaśniać dlaczego jest tak jak jest oraz ewentualnie umożliwić analizę skutków podejmowanych decyzji gospodarczych.

EMPIRYZM ZDROWEGO ROZSĄDKU- (Empiryzm fotelowy) teoria bez pomiaru- nie interesuje nas zależność ilościowa (liczbowa) jedynie sam fakt
(np: coś rośnie → coś spada).

AD. 2

WERYFIKACJA MODELU- empiryzm zdrowego rozsądku, analiza danych statystycznych, metody ekonometryczne, itp.

DANE- statystyka ekonomiczna-źródła, wiarygodność, obróbka i prezentacja, wskaźniki (indicators)

EKONOMETRIA- gałąź ekonomii stosująca metody statystyczne do mierzenia i szacowania zależności ekonomicznych. EKONOMETRIA rozwijała się w oparciu o BIOMETRIĘ. Wykrywa ona zależności między zmiennymi ekonomicznymi; nie rozstrzyga dlaczego one są akurat takie a nie inne.

Ekonometria musi najczęściej stosować założenie ceteris paribus [inne rzeczy bez zmian]

Forma prowadzenia analizy ekonomicznej prowadzi do następującego podziału EKONOMII:

E. LITERACKA: forma słowna, opisowa, analiza kontekstowa.

E. SFORMALIZOWANA- forma matematyczna (zróżnicowany stopień założeń) analiza bezkontekstowa.

E. MATEMATYCZNA- skrajnie sformalizowana forma prowadzenia analizy ekonomicznej; tworzenie oraz badanie modeli matematycznych zjawisk ekonomicznych. W ekonomii matematycznej - obserwowany fragment - jest zapisywany w formie zależności matematycznych. Matematyka - jest tym językiem, który uściśla pojęcie ekonomiczne.

Język: równania, nierówności, relacje, zależności funkcjonalne...

Modele Matematyczne zjawisk ekonomicznych ≈ Teoria Ekonomiczna w formie matematycznej

WYKŁAD II 27.09.2003 r.

W. Petty autor książki pt.: „Arytmetyka polityczna” ok. 1676, postulował stosowanie wielkości ekonomicznych; przed nim w ekonomii nie było żadnych liczb.

F. Quesnay 1759 -„Tablice ekonomiczne” fizjokrata, praca ta ma charakter ilościowy, zajmuje się przepływami makroekonomicznymi.

Fizjokrata - kieruje się zasadami: trzeba badać gospodarkę, wykrywać prawa, tworzyć teorię, prekursorzy ekonomii sformalizowanej.

A.A. Cournot- prekursor ekonomi matematycznej -1838 „Badania nad zasadami matematycznymi teorii bogactwa”;

A. Smith -1776 „Badania nad naturą i przyczynami bogactwa narodów”

Ekonomia powinna formułować prawa ilościowe, które powinny opisywać związki między wielkościami ekonomicznymi.

Cournot zajmował się analizą monopolu i oligopolu.

Zmienność wielkości ekonomicznych.

Zmienność wielkości ekonomicznych

x - przedział C ⊂ R

np.: [a, b], [a, b), (a, b), R ₊:= (0,∞) -liczby nie ujemne, R ₊₊ := (O, ∞)- liczby dodatnie

f : X→ R y = f{x}

Mf{x) := f '{x) wartość krańcowa f (w punkcie x) (pochodna)

Af{x) := f{x}/ x wartość średnia f (w p. x) (x≠0 np. do kosztów produkcji)

Ff{x} := f{0) część stała f (np.: koszty stałe)

Vf{x) := f{x) - f{0) część zmienna f

E^f(x) :=
elastyczność f względem x

Łączenia A(Vf)(x) = [f(x)-f(0)] / x

f'(x) ≈ [f(x+Δx)-f(x)] / Δx (ale tylko dla małych Δx)

f'(x) = Mf(x)

Mf(x) ≈ [f(x+Δx)-f(x)]/Δx

∆x - mała zmiana x

∆f{x) := f(x +∆x) - f(x) - odpowiada zmianie x o ∆ x. zmiana wartości funkcji f

∆f(x) ≈ Mf(x) . ∆x (równość przybliżona)

"mała" i ,,≈" - w sensie rachunku różniczkowego

Przykład: C : R ₊→ R ₊₊ funkcja kosztu,

tzn. "ilość produkowana" → "koszt wytworzenia tej ilości"

q → C(q) [tak jak by tu było napisane f(x)]

MC(q) - koszt krańcowy przy poziomie produkcji q

Gdy ∆q = 1 jest małą zmianą q: ∆C(q) ≈ MC(q) =1

koszt krańcowy ≈ koszt wyprodukowania dodatkowej jed­nostki (przy poziomie produkcji q) .

Elastyczność popytu

Przykład: D : R ₊ → R ₊₊ funkcja popytu

"cena" → "ilość, którą konsumenci przy tej cenie kupią"

E^D(p) - elastyczność cenowa popytu przy cenie p

E^D(p) ≈

Zakładamy prawo popytu w wersji różniczkowej:

popyt jest nie tylko malejącą funkcją ceny, ale też D'(p) < 0.

Stąd: elastyczność cenowa popytu < 0.

Znak elastyczności określa - cena, popyt i pochodna (cena + popyt+ pochodna).

Popyt przy danej cenie p popyt D jest:

Elastyczny ≡ |E^D(p)| > 1

Jednostkowo elastyczny ≡ |E^D(p)| = 1

Nieelastyczny ≡ |E^D(p)| < 1

­­Elastyczność funkcji potęgowej:

f(x) = c x^α elastyczność nie zależy od x

gdzie x ∈ R ₊₊; α ≠ 0 oraz c - ustalone liczby

E^f(x) = α (stała, niezależna od x)

i odwrotnie

E^f(x) = α (stała) ⇒funkcja f jest funkcją potęgową

Wartość krańcowa i elastyczność

∆x := mała zmiana x; ∆f(x) := f(x + ∆.x) - f(x)

Mf(x) := f'(x), E^f(x) :=

Ponieważ ∆f(x) ≈ Mf(x) *∆.x, to dla. ∆x≠ 0

Mf(x) ≈

Mf(x) ≈

Analogicznie, gdy ∆.x ≠0, x ≠0, f(x) ≠0:

E^f(x) ≈

E^f(x) ≈

% ≡ *
(mnożenie przez
)

Gdy x zmieniło się o ξ %, to y = f(x) zmieniło się o η%.

(Gdy cena rośnie o 5% to popyt spada o 7,5%)

X_nowe = x+ξ % x, (nowa cena = stara + 5%tarej)

Y_nowe = y + η% y = f(x) + η% f(x) (nowy popyt = stary - 7,5% starego)

∆x = ξ % x, (wzrost ceny = 5% starej)

∆f(x) = η% f(x)

E^f(x) ≈ czyli E^f(x) ≈

Mf(x) ≈
= η%f(x) / ξ%x,

czyli Mf(x) ≈
* Af(x) Mf(x) = E^f(x)*Af(x)

[(Popyt) 5/-5 (cena) = -1]

WYKŁAD III 04.10.2003 r.

Teoria Firmy

PODSTAWOWE INSTYTUCJE MIKROKONOMICZNE

1. Gospodarstwa domowe

2. Firmy (przedsiębiorstwa)

GOSPODARSTWA DOMOWE nabywają i konsumują towary głównie za środki uzyskane ze sprzedaży swojej pracy.

FIRMA produkuje (wytwarza) towary za pomocą towarów nabywanych od innych firm, towaru "PRACA" (in. siła robocza) nabywanego od gospodarstw domowych a także z innych nakładów.

NEOKLASYCZNA TEORIA EKONOMII zakłada, że celem firmy jest MAXYMALIZACJA zysku z produkcji (funkcja jednej zmiennej)

WYKRES 1.

Maksimum lokalne- największe z danego zakresu

Maksimum globalne- największe z całości

f:(a,b) → R ma x₀∈(a,b) max lokalne ∃ δ>0 takie, że f(x₀) ≥ f(x) dla x∈(x₀-δ; x₀+δ)

OZNACZENIA:
∃- istnieje
∃!- istnieje dokładnie jedno
∀- dla każdego
&- i, oraz

WARUNEK KONIECZNY I RZĘDU (pierwsza pochodna):

Jeśli f(a,b) → R jest różniczkowalna i ma w x₀∈(a,b) max lokalne, to f'(x₀)=0

WARUNEK II RZĘDU (pochodna druga)

WARUNEK DOSTATECZNY II RZĘDU

Jeśli dodatkowo założymy, że f jest dwukrotnie różniczkowalna, to f''(x₀)≤0

Niech f dwukrotnie różniczkowalna- f'' ciągła, wówczas

[f'(x₀)=0 & f''(x₀)<0 ⇒ f ma max lokalne w x₀]

PUNKTY KRYTYCZNE FUNKCJI

ZERA pochodnej, czyli takie, że f'(z)=0- punkty krytyczne f

NEOKLASYCZNA TEORIA FIRMY

Upraszczające założenia ogólne:

• Firma produkuje jeden towar, przy czym może wytwarzać dowolną jego ilość q, gdzie q∈R₊ (nieujemna); q- poziom produkcji firmy

• Firma działa w jednym okresie czasu, w którym nic się nie zmienia- firma nie myśli o przyszłości

• Firma zna swoją funkcję kosztu C, a więc koszt całkowity C(q) produkcji q jednostek wytwarzanego przez siebie towaru

• Firma zna swoje "otoczenie rynkowe" (warunki działania); w szczególności firma zna cenę zbytu P(q), jaką uzyska sprzedając (w rozpatrywanym okresie) q>0 jednostek wytwarzanego towaru.

• Zakładamy, że firma wszystko co wytworzy, może sprzedać po takiej cenie

NEOKLASYCZNY CEL FIRMY-MAKSYMALIZACJA ZYSKU

ZYSK = PRZYCHÓD - KOSZT

Zysk zależy od q- Π (q)- zysk osiągany przy poziomie produkcji q

Przychód (utarg) R przy poziomie produkcji q:

Jeśli q=0 to R(q) = 0 R(q) = q * P(q) gdy q > 0

C(q) =koszt wytworzenia q jednostek towaru

Π (q) = R(q) - C(q)

CEL FIRMY- dobrać taki poziom produkcji
> 0 by Π(
) były największe

Decyzje firmy dotyczące wyceny poziomu produkcji q:

CEL: produkcja na poziomie
> 0 dla którego Π (
) jest największe (max zysku)

- optymalny poziom produkcji

Firma produkując
jednostek jest w stanie równowagi. Zmiana in będzie zmniejszać zysk.

Warunek konieczny I rzędu:

Π'(
) = 0 czyli R'(
) = C'(
) tzn. MR(
) = MC(
)

MR(
)- wartość krańcowa przychodu (przychód krańcowy)

MC(
)- wartość krańcowa kosztu (koszt krańcowy)

(Słownie:) Jeśli
jest maksymalizującym zysk poziomem produkcji, to przychód uzyskany ze sprzedaży dodatkowej jednostki jest równy kosztowi jej wytworzenia.

Warunek konieczny II rzędu:

Π''(
) ≤ 0 czyli R''(
) ≤ C''(
)

Warunek dostateczny II rzędu:

Π''(
) < 0 czyli R''(
) <C''(
) ORAZ Π'(
) = 0 czyli R'(
) = C'(
)

ANALIZA RENTOWNOŚCI

Szukamy I poziomu produkcji przy którym zysk jest równy 0

Firma (P, C) gdzie P= Cena zbytu, C= funkcja kosztu

P: R₊₊ → R₊₊ funkcja nierosnąca, inaczej malejąca w szerszym sensie

C: R₊ → R₊ rosnąca (ściśle)

Dla q > 0, Π (q) = q*P(q) - C(q) a Π(0) = -C(0) - (q*P(q) = R(q)

PRÓG RENTOWNOŚCI - q_b

q_b > 0 taki, że Π (q) = 0

Dla q > 0, Π(q) = q*P(q) - C(q) = q [ P(q) - AC(q) ]

A- wielkość średnia, przeciętna

AC(q) =

Π (q) < 0 gdy P(q) < AC(q) - STRATA

Π (q) < 0 gdy P(q) > AC(q) - ZYSK

Π (q_b) = 0 gdy P(q_b) = AC(q_b) - PRÓG RENTOWNOŚCI

Szukamy II poziomu produkcji, przy którym zysk jest równy 0.

(zakładam, że zysk ujemny jest taki jak w przypadku nie prowadzenia żadnej produkcji)

PRÓG PODJĘCIA DZIAŁALNOŚCI - q_s

q_s > 0, taki, że Π(q_s) = Π(0)

C(q) = VC(q) + FC gdzie FC = C(0)

VC - część zmienna funkcji kosztu (koszt zmienny)

FC - część stała funkcji kosztu (koszt stały)

[koszt całkowity C = koszt zmienny VC + koszt stały FC

Π (q) = q*P(q) - VC(q) - FC = q [P(q) - AVC(q) ] - FC -średni koszt zmienny

C.D.N.

WYKŁAD IV 11.10.2003 r.

PODSTAWOWE STRUKTURY RYNKOWE

STRUKTURA RYNKOWA - forma organizacji produkcyjnej, określająca zachowanie się uczestników na rynku

Można wyróżnić dwie podstawowe struktury:

1. Konkurencja doskonała

2. Konkurencja niedoskonała

• monopol

• oligopol

• konkurencja monopolistyczna

Kryteriów podziału może być wiele, jednym z nich może być „ilość sprzedających”
(firm produkcyjnych)

MONOPOL - jeśli jedna firma ma ¾ udziału na rynku

OLIGOPOL - kilka firm, które wzajemnie ustalają reguły lub rywalizują

KONKURENCJA MONOPOLISTYCZNA - gdy jeden produkt sztucznie odbierany jest przez konsumentów jak kilka towarów -substytuty

J. Robinson-w 1933 r. wydała książkę „O ekonomice konkurencji monopolistycznej”, twórczyni terminu MONOPSON (struktura w której jest tylko 1 nabywca towaru) oraz DYSKRYMINACJA CENOWA (firma tworzy sztucznie z jednego towaru kilka innych, np.: bilety normalne i ulgowe).

E. Chamderlin- 1933 r. „Teoria konkurencji monopolistycznej”, podkreślał rolę REKLAMY oraz odkrył rolę MARKI

Stackerberg- 1934 r. „Formy rynku i równowaga”, sklasyfikował formy rynku przez pryzmat ilości nabywców i producentów

WIELKOŚCI

D: R₊₊ R₊₊ funkcja popytu [rynkowego]

„cena p” → „ilość q towarów, którą konsumenci kupią” po cenie p [prawo popytu - popyt funkcja malejąca; pochodna funkcji popytu jest ujemna, czyli ujemna w każdym punkcie]

Zakładamy prawo popytu w wersji różniczkowej D'(p) < 0

FUNKCJA ODWROTNA DO F. POPYTU

stąd ∀q > 0 ∃! p > 0 t. że q =D(p)

a więc ∃ funkcja odwrotna D^-1 do f. popytu D i q =D(p) ⇔ p =D^-1(q);

fD^-1 ma pochodną (D^-1)'(q) < 0 [wykres tej funkcji powstaje przez obrót osi]

D^-1: R₊₊ R₊₊ odwrotna f. popytu

„ilość q” → „cena p, którą konsumenci płacą gdy na rynku jest q jednostek towaru”

MONOPOL

Cena towarów uzależniona jest od ilości wyprodukowanych towarów. Monopolista podejmuje decyzje o ilości produkcji a na podstawie prawa popytu ustala cenę.

Gdy produkcja
> 0 max zysk to MC(
) = MR(
)

p = D^-1(q) = P(q) Przychód = ilość * cena R(q) = qP(q)

MR(q) = (R(q))' =(qP(q))' =(q'*D^-1(q))' = q*(D^-1(q))' + 1*D^-1(q)

Poziom produkcji monopolistycznej q wyznacza całkowitą ilość dostępną na rynku a to wyznacza cenę p: D^-1(q) Monopolista jest cenotwórcą (price maker). Monopolista zakłada, że jego cena zbytu P jest wyznaczona przez odwrotną funkcję popytu D^-1 tzn. ∀q > 0: P(q)= D^-1(q)

Dla monopolu: MC(
) =
(D^-1)' |
| + D^-1(
) < D^-1(
)

Czyli MC(
) < ceny [warunek konieczny….???]

KONKURENCJA DOSKONAŁA

Producent jest biorcą ceny i jego działanie nie zmienia ceny.

Cena zbytu =stała cena rynkowa
(„going price”-cena idzie) czyli P(q)-
niezależnie od q. Mała firma w warunkach doskonałej konkurencji jest CENOBIORCĄ („price taker”)

(R(q))' = (
*q) =

MC(
) =
-koszt krańcowy jest równy cenie sprzedaży.

KONSUMENCI

TEORIA WYBORU KONSUMENTA

ZAŁOŻENIA:

• jeden racjonalny konsument o sprecyzowanych upodobaniach

• towary: datowane i zlokalizowane

• towary (doskonałe) podzielne (liczba rzeczywiste nieujemne)

n - ustalona liczba naturalna (reprezentująca liczbę towarów na świecie)

Rⁿ- przestrzeń n -wymiarowa

Elementy Rⁿ wektory n- wymiarowe

wektor n- wymiarowy- uporządkowany układ n liczb rzeczywistych: x= (x₁, x₂,...,x_j,...,x_n)

x_j = jota współrzędna wektora x(j= 1,2,...,j,...,n)

x = y ∀_j = 1,2,...,j,...,n; x_j = y_j (x,y ∈ Rⁿ)

x ≥ y ∀_j = 1,2,...,j,...,n; x ≥ y_j (x,y ∈ Rⁿ )

x > y ∀_j =1,2,...,j,...,n; x > y_j (x,y ∈ Rⁿ )

np. wektor z elementami: (1:4) ≥ (1,2) bo 1 ≥ 1 i 4 ≥ 2

wektory mogą być nieporównywalne: (1:2) ??? (2:1)

(0,0,...,0) ∈ Rⁿ 0 -będzie oznaczony

x ≥ 0 -wektory nieujemne- takie, które mają wszystkie wektory nieujemne

x > 0 - wektory dodatnie- wszystkie współrzędne są większe od zera

Rⁿ₊ :={x ∈ Rⁿ | x ≥ 0 } -zbiór elementów

PREFERENCJE KONSUMENTA

Poniżej x, y, z ∈ Rⁿ₊ są dowolnymi wiązkami towarów.

RELACJA PREFERENCJI: „w.t. x” preferowana nie mniej niż „w.t. y”

- preferencja

[x y- w.t. x preferowane nie mniej niż w.t. y]

założenia:

• jeżeli konsument ma 2 w.t., pierwszą preferuje nie mniej niż drugą

• jeżeli konsument ma 2 w.t. drugą preferuje nie mniej niż pierwszą

• jeżeli konsument ma 3 w.t.

CECHY:

• x y lub y x [spójność]

• x x [zwrotność- jeden towar]

• x y & y z x z [przechodniość]

RELACJE OBOJĘTNOŚCI (indyferencji)

x P y - Konsument nie odróżnia w.t. x od w.t. y, przy relacji preferencji określane:

x P y ⇔ x y & y x konsekwentnie:

x P y y P x

x P x

x P y & y P z x P z

WYKŁAD IV 25.10.2003 r.

RELACJE SILNEJ PREFERENCJI

x ≻ y x y & y x x ≻ y - w.t. x preferowana bardziej niż w.t. y

x ≻ y x y & x P y - P -nie jest prawdą, że x odróżnialne od y

[Albo x ≻ y, albo x P y albo y ≻ x, albo y x]-sprawdzić

Dla żadnego x nie jest prawdą, że x ≻ x

[(x y & y ≻ z) lub ( x ≻ y & y z)] x ≻ z

Jeżeli pierwszy towar jest preferowany nie mniej niż drugi a drugi bardziej niż trzeci to pierwszy jest preferowany bardziej niż trzeci.

POWIERZCHNIE (KRZYWE) OBOJĘTNOŚCI

x- ustalone w.t. (koszyk towarów- zbiór)

Konsument nie odróżnia towarów.

[x: = {y∈ Rⁿ₊ | y P x} - powierzchnia obojętności wyznaczone przez x to zbiór towarów y nieodróżnialnych przez konsumenta od x

{ I x} x∈ Rⁿ₊ - mapa obojętności x₂

n = 2 (n- ilość towarów) z

z P y x

x P y

x P z x₁

1. {y∈ Rⁿ₊ | y ≻ x} -zbiór w.t. preferowany bardziej niż x

2. {y∈ Rⁿ₊ | y x} -zbiór w.t. preferowany nie mniej niż x

3. {y∈ Rⁿ₊ | x ≻ y} - zbiór w.t. preferowany mniej niż x

SUBSTYTUTY DOSKONAŁE

Konsument jest gotów zastąpić pierwszy towar drugim wg stałej stopy np.: 1:1, 1:2.
(zapalniczki czerwone i zielone)

TOWARY DOSKONALE KOMPLEMENTARNE

Konsumowane zawsze w stałym stosunku np.: 1:1. 1:2.
(buty lewe i prawe)

x =(x₁, x₂) ∈ Rⁿ₊ y =(y₁, y₂) ∈ Rⁿ₊ -dowolne

Kiedy konsument preferuje pierwszy zestaw towarów nie mniej niż drugi:

x y min(x₁, x₂) ≥ min (y₁, y₂)

TOWARY NIECHCIANE („bads”)

Konsument jest gotów zwiększyć spożycie niechcianego towaru o ile zostanie mu to zrekompensowane zwiększeniem ilości towaru, który lubi.
(czekoladki i tran)

x₁ -czekolada x₂- tran

TOWARY NEUTRALNE

Towary, na których konsumentowi nie zależy

x₂ -obojętny towar

NASYCENIE (błogostan)

Istnieje najbardziej preferowany zestaw towarów

(lody czekoladowe i krem czekoladowy)

x∈ Rⁿ₊
(x₁, x₂)

PUNKT NASYCENIA- taki zestaw towarów
preferowany nie mniej niż jakikolwiek inny zestaw z całej przestrzeni towarów.

GRZECZNIE ZACHOWUJĄCE SIĘ PREFERENCJE

1. MONOTONICZNOŚĆ

1. Monotoniczność preferencji
   Jeden zestaw towarów zawiera co najmniej tyle każdego towaru co koszyk drugi zawierający jeden towar
   -monotoniczna ≡ x, y∈ Rⁿ₊ ; y ≥ x y x
   nie przeszkadza zwiększona ilość towaru- „od przybytku głowa nie boli”

2. Ścisła monotoniczność preferencji (zachłanność konsumenta)
   - ściśle monotoniczna ≡ x, y∈ Rⁿ₊ ; y ≠ x & y ≥ x y ≻ x
   ścisła monotoniczność = Monotoniczność

PRZESTRZEŃ TOWARÓW

2. WYPUKŁOŚĆ PREFERENCJI

x, y∈ Rⁿ₊ -dowolne wektory; x∈ R -dowolna liczba

x =(x₁, x₂,…x_j,…,x_n), y =(y₁, y₂,…,y_j,…,y_n)

x + y: =(x₁ + y₁, x₂ + y₂,…,x_j + y_j,…,x_n + y_n)

xx: =( xx₁, xx₂,…xx_j,…,xx_n )

(x, y∈ Rⁿ₊ & x∈ Rⁿ₊ ) xx∈ Rⁿ₊

Rozpatrzymy p x: =xx + (1-x)y

Gdy x∈ R - p x to p. prostej przechodzącej przez x i x

Gdy x∈[0, 1] -p x to p.odcinka x- y

Gdy x∈(0, 1) -p x to p. wewnętrzny odcinka x- y

WYKŁAD IV 08.11.2003 r.

WYPUKŁOŚĆ PREFERENCJI

-wypukła ≡ x, y, z ∈ Rⁿ₊

x ∈ [0, 1]: (y x & z x) xy +(1- x) z x

relacja jest wypukła wtedy i tylko wtedy () gdy dla każdego x należącego do przestrzeni towarów ( x∈ Rⁿ₊ ), które są preferowane nie mniej niż x {y |y x}jest wypukła

wypukła () ( x∈ Rⁿ₊ ): {y |y x}

ŚCISŁA WYPUKŁOŚĆ PREFERENCJI

ściśle wypukła ≡ x, y, z∈ Rⁿ₊ x∈ (0, 1):

(y ≠ z, y x, z x) x+(1-x) ≻ x

Ścisła wypukłość pociąga za sobą wypukłość ś. wypukłość = wypukłość

Relacja preferencji wypukła jest ściśle wypukła wtedy i tylko wtedy gdy żadna krzywa obojętności tej relacji nie zawiera odcinka prostej:

Dla dowolnej funkcji u: Rⁿ₊-R zdefiniowany u x ny u(x) ≥ u(y) (x, y ∈ Rⁿ₊ - dowolne)

jest relacją preferencji. Funkcja u definiuje (generuje) relację preferencji u

x P u y: u(x) = u(y); x ≻ u y: u(x) > u(y)

FUNKCJA UŻYTECZNOŚCI

-dana relacja preferencji

Funkcja u: Rⁿ₊ -R jest funkcją użyteczności, przedstawiająca (reprezentująca)
≡ x, y ∈ Rⁿ₊ x y u(x) ≥ u(y) (czyli = u)

Liczba(x)- użyteczność w.t. x

Przykłady:

• Substytuty doskonałe- stopa wymiany: a:b u(x₁, x₂): = bx₁ + ax₂ przedstawia odpowiadającą substytutom doskonałym relację preferencji

• 
  Towary komplementarne- proporcje konsumpcji a:b u(x₁, x₂): =min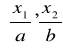
  przedstawia odpowiadającą towarom komplementarnym relację preferencji
  u(x)
  w(x) = a+ b u(x) >0

ISTNIENIE FUNKCJI UŻYTECZNOŚCI

n=2 , x=(x₁, x₂), y= (y₁, y₂); zdefiniowano tak:

• y x y₁ >x₁ lub (y₁= x₁ & y₂ ≥ x₂)

porządek leksykograficzny- „słownikowy”

Tak zdefiniowany związek towarów jest relacją preferencji na R²₊!

Ix = {x} krzywa obojętności jest punktem x dla relacji preferencji zdefiniowanej przez porządek leksykograficzny.

Nie istnieje funkcja użyteczności przedstawiająca tą relację.

DLA JAKIEJ RELACJI PREFERENCJI ISTNIEJE FUNKCJA UŻYTECZNOŚCI I CO JEST POWODEM?

CIĄGŁOŚĆ PREFERENCJI FUNKCJI

Odległość x od z

x= (x₁, x₂,…,x_j,…x_n) ∈ Rⁿ

z= (z₁, z₂,…, z_j,…z_n) ∈ Rⁿ

|x-z|: = max {|x_j -z_j|: j = 1,2,…,n bezwzględnej różnic

x = (0, 1, 2) z = (-1, 3, 1)

0-(-1) = | 1 | 1-3= | 2 | 2-1= | 1 | WYNIK: |x-z| 2

|x-z|: = max {|x₁ - z₁|, |x₂ - z₂|,…|x_j - z_j|,…|x_n - z_n|}

x,y,z :1: |x-z| ≥ 0;

2 |x - z| =0 x=z;

3 |x - z| = |z - x|

4 |x - z| ≤ |x - y| + |y - z|

WYKŁAD IV 15.11.2003 r.

C.D.

Dlaczego dla pewnych relacji preferencji nie można przedstawić użyteczności?

Przypomnienie: ciągłość preferencji występuje gdy relacja trójkąta odległości wektora x od y jest

mniejsza od sumy odległości x, y, z.

Różnice między zestawami towarów są traktowane jak odległość między wektorami

- ciągła ≡ x, y ∈ Rⁿ₊ takiego, że x ≻ y potrafimy znaleźć

∃ ε > 0 takie, że x' ∈ Rⁿ₊ & y' ∈ Rⁿ₊

|x' - x| ≤ ε & |y' -y| ≤ ε x' ≻ y'

Małe zmiany w ilościach towarów nie zmieniają relacji.

x- piwo, y- bułki zestaw ze zmniejszoną ilością x- piwa nie będzie preferowany bardziej niż zestaw z większa ilością piwa.

Preferencje opisane porządkiem leksykograficznym nie są ciągłe

CIĄGŁOŚĆ FUNKCJI

f: x R^k - dane gdzie x ⊂ Rⁿ, k- liczba naturalna (lub używany częściej n),
x- przestrzeń towarów Rⁿ₊

f ciągła ≡ x ∈ X ε > 0 ∃ б > 0 takie, że z ∈ x

|x - z| ≤ б f(x) - f(x) ≤ ε

DOMKNIĘTOŚĆ ZBIORÓW

z ∈ Rⁿ , x ∈ Rⁿ -dowolne

z leży dowolnie blisko zbioru X

z leży dowolnie blisko zbioru X ≡ ∈ > 0 ∃ x ∈ X takie, że |x - z| ≤ ε

odległość nie przekracza ε

UWAGA: Jeżeli z jest elementem zbioru X- leży dowolnie blisko zbioru X

Zbiór X ⊂ Rⁿ - domknięty ≡ każdy z ∈ Rⁿ który leży dowolnie blisko X musi należeć do X

Przykład zbioru domkniętego: Ø, Rⁿ₊ , Rⁿ , zbiory skończone są domknięte

TWIERDZENIE:

jest ciągła ≡ x ∈ Rⁿ₊ zbiór w.t. preferowanej nie mniej niż x|
tzn.: zbiór {y∈ Rⁿ₊ (y x)} oraz zbiór w.t. preferowanej nie bardziej niż
tzn..: zbiór {y∈ Rⁿ₊ (x y)} SĄ DOMKNIĘTE
[ciągłość relacji preferencji to DOMKNIĘTOŚĆ pewnych zbiorów związanych z tą relacją]

u : Rⁿ₊ R -daną funkcją u jest ciągła u jest ciągła [x uy u(x) u(y)]

ISTNIENIE FUNKCJI UŻYTECZNOŚCI

TWIERDZENIE (Gerard DEBREU, 1954 r.)
-dana relacja preferencji || jest ciągła ∃ funkcja użyteczności u: Rⁿ₊ R reprezentująca . Funkcja u musi być ciągła

FUNKCJA POPYTU

KONSUMENT: opisuje GO relacja preferencji oraz posiadany zasób pieniężny M 0

Zasób jest tu pewnym atrybutem liczbowym towaru

Niech p_i oznacza cenę j-tego towaru

p= (p₁, p₂,…p_j, …p_n) ∈ Rⁿ₊ -wektor cen towarów (w.c.) należy do przestrzeni cen

Zbiór X ⊂ Rⁿ -ograniczony ≡ ∃ β>0 x∈ X i=1,2,…n:

-β ≤ x_i ≤ β x= (x₁, x₂, ..., x_n)

TWIERDZENIE (K. Weierstraβ)

X- zbiór domknięty i ograniczony ⊂ Rⁿ & u: x R- dana funkcja ciągła

Funkcja taka osiąga max na X tzn:

∃
∈ X : u (
) ≥ u (x), x ∈ X

u (y) ≥ u (x) y x

twierdzenie: X- zbiór domknięty i ograniczony ⊂ Rⁿ & dana ciągła relacja preferencji. Wówczas

∃
∈ X :
x, x ∈ X

ILOCZYN SKALARNY

x = x= (x₁, x₂,…,x_j,…x_n) -zestaw towarów (w.t.)

p= (p₁, p₂,…p_j, …p_n) - wektor cen („ceny”)

p·x : = p₁ x₁ + p₂ x₂ +…+ p_j x_j +…+ p_n x_n
p·x- iloczyn skalarny p oraz x (wartość w.t. x przy cenie p)

p ∈ Rⁿ₊ -w.c. & x ∈ Rⁿ₊ -w.t.

wówczas: p·x ≥ 0
p > 0 & x > 0 p·x > 0

ROLA PIENIĄDZA

Jeśli konsument posiada zasób pieniężny M ≥ 0 to przy cenach towarów p może nabyć dowolną
w.t. x, której wartość p·x nie przekracza M.

p ∈ Rⁿ₊ -dany wektor cen towarów („ceny”) M ≥ 0 -dany zasób pieniężny konsumenta

B (p;M) : ={x ∈ Rⁿ₊ | p·x ≤ M} B (p;M) -zbiór ograniczeń budżetowych konsumenta.

WŁAŚCIWOŚCI TEGO ZBIORU:

1. B (p;M) - domknięty

2. B (p;M) ≠ 0 -nie pusty

3. B (p;M) - ograniczony p > 0 (ceny dodatnie)

Twierdzenie (WAŻNE) : Niech p > 0, M ≥ 0 i - dana ciągła relacja preferencji (wtedy B(p,M) jest domknięty i ograniczony) wówczas:
∃
∈ B( p;M) :
x₁ x ∈ B( p;M)

Słownie: Gdy ceny towarów są dodatnie a relacja preferencji konsumenta ciągła, to istnieje w.t. x, której wartość przy tych cenach nie przekracza zasobu pieniężnego konsumenta i która jest przez niego preferowana nie mniej niż każda inna w.t. x, której wartość przy tych cenach nie przekracza jego zasobu pieniężnego.

WYKŁAD IV 29.11.2003 r.

OPTYMALNY WYBÓR KONSUMENTA

w.t.
-optymalny wybór konsumenta przy cenach p zasobie M (OWK przy (p,M))

Jeśli OWK
>0 , to mówimy o optimum wewnętrznym

Jeśli OWK
0 , to mówimy o optimum brzegowym

W dalszym ciągu zawsze zakładamy spełnienie założeń Twierdzenia o istnieniu OWK a więc p>0 , M 0 oraz ciągłości

TW [Warunek konieczny]

Niech
- OWK przy (p,M) , [a więc
∈ B (p,M)]

Wówczas , y∈ Rⁿ₊ : y ≻
py > M

to
jest OWK przy (p,M)

TWIERDZENIE [Warunek dostateczny OWK]

Niech
∈ B (p,M) Jeśli y∈ Rⁿ₊ : y ≻
p*y > M

to
jest OWK przy (p,M)

Jednoznaczność OWK

Następujące warunki są równoważne:

a) ∃
∈ B(p,M) :
≻ x , x∈ B(p,M), x ≠

b) ∃ !
∈ B(p,M) :
≻ x, x ∈ B(p,M)

Linia ograniczeń budżetowych konsumenta

L(p,M) := {x∈ Rⁿ₊ | p*x = M

Składa się z tych w.t. x, których wartości p*x przy cenach p jest równa zasobowi pieniężnemu konsumenta M

TWIERDZENIE Istnienia i jednoznaczności OWK

Niech będzie daną ciągłą relacją preferencji. Załóżmy też, że jest monotoniczna i ściśle wypukła wówczas p >0, M ≥ 0

a)
x, x ∈ B(p,M)

b)
∈ L(p,M)

c) odwzorowanie (p,M)
jest ciągłe

Odwzorowanie (p,M)
czyli:

(dodatnie ceny, zasób pieniężny) OWK przy (p,M) - funkcja popytu konsumenta

dziedzina: zbiór par (p,M) z p>0 , M ≥ 0

wartości: w przestrzeni towarów

Wartość funkcji popytu - popyt

Oznaczenia: d - funkcja popytu: d(p,M) - popyt.

Popyt
przy (p,M) należy do L(p:M) czyli:

p*d(p,M)=M („konsument wydaje wszystko”)

-„dodatnia jednoznaczność stopnia 0”

Mówiąc o popycie lub funkcji popytu zawsze zakładamy spełnienie założeń Twierdzenia o istnieniu i jednoznaczności OWK.

I p = (p₁, p₂)

x = (x₁, x₂)

p₁ x₁ + p₂ x₂ ≤ M

p₁ x₁ + p₂ x₂ = M

Zbiór ograniczeń budżetowych konsumenta

x₂

przestrzeń towarów

zbiór ograniczeń budżetowych

p₂

p₁ x₁

ilość pierwszego towaru

Optymalny wybór konsumenta

x₂

B(p,M)

x₁

Zmiana zasobu pieniężnego konsumenta

Jak zmienia się wielkość konsumpcji (popyt konsumenta) przy stałych cenach
i zmiennym

zasobie pieniężnym M konsumenta?

Popyt

Ścieżka wzrostu dochodu (wszystkie towary)

Jest to funkcja
R₊ Rⁿ₊

(lub jej obraz w przestrzeni towarów)

Krzywa Engla (ustalony towar)

Dla j-tego towaru (j-ustalone)

x₂

ścieżka wzrostu dochodu

przestrzeń towarów

M₁ M₂ M₃ M₄ x₁

WYKŁAD IV 13.12.2003 r.

Teoria Równowagi Ogólnej TRO

„Równowaga to stan gospodarki, w którym nie zachodzą zmiany w układzie jej elementów i nie działają siły mogące ten stan zmienić”

W praktyce układ cen przy, którym popyt nie przekracza podaży bądź się z nią zrównuje.

Ogólna TR - jednocześnie analizujemy rynki wszystkich towarów (rynek jako całość)

Szczególna TR - analizujemy rynek ustalonego towaru w oderwaniu od reszty gospodarki (czyli stosując zasadę ceteris paribus)

TRO przedstawia ogólny obraz konsumpcji produkcji i wymiany w całej gospodarce jest to teoria mikroekonomiczna. Bada powstanie i trwanie RO

A. Smith (1776) - „przeczuwał” istnienie RO

L. Warlas (1874) - sformułował podstawy TRO wraz z V. Pareto (1896-97, 1911) Szkoła Lozańska - „ojcowie” Ekonomii Matematycznej

F. Edgeworth(1881)

K. Arow(LNN172; G Debren(LNN1983)(1954) oraz L.McKanzie1954 - poprawne uzasadnienie istnienia równowagi ogólnej

Modle wymiany teorii rónowagi ogólnej

(Arrow - Hurwicz 1958)

• n i m - ustalone liczby naturalne

• n - liczba towarów ;
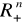
  - przestrzeń towarów

• m - liczna konsumentów („uczestników ekonomii”)

i-tego konsumenta charakteryzuje:

1. relacja preferencji i-tego konsumenta oraz

2. wⁱ ∈ Rⁿ₊ - zasób początkowy i-tego konsumenta

Ceny towarów mogą być zerowe ale nie wszystkie naraz!

- przestrzeń cen niezerowych

Stosunki wymienne: jednostkę i-tego towaru można wymienić na
jednostek k-tego towaru

- podaż całkowita

- zbiór budżetowy i-tego konsumenta

- zawiera dokładnie te zestawy towarów, które konsument może nabywać w rozpatrywanej gospodarce.

x₂

w₂ w

w

px=pw

w₁

Założenie o istnieniu popytu dla każdego konsumenta

∃ !
takie że

x

Ww (określony jednoznacznie dla danych cen p) zestaw towarów
to popyt i-tego konsumenta oznaczonego dⁱ (p)

dⁱ - funkcja popytu („indywidualnego”) i-tego konsumenta.

Założenie: Funkcje dⁱ : Rⁿ₊ \ (0) Rⁿ₊ są ciągłe

- popyt całkowity przy cena p

- funkcja popytu całkowitego popyt całkowity d jest więc ciągłą funkcją cen p

- nadwyżka popytu całkowitego

(nadwyżka popytu := popyt całkowity - podaż całkowita)

- czyli j-te współrzędne wektora g(p), to nadwyżka popytu na j-ty towar

gdzie
to j-ta współrzędna d(p) (czyli popyt całkowity na j-ty towar) a w_j to j-ta współrzędna w *czyli podaż całkowita j-tego towaru)

Nadwyżka popytu g jest ciągłą funkcją cen p.

Mówimy, że popyt jest zaspokojony przy cenach ceny p^*

gdy

(Popyt na żaden towar nie przekracza podaży tego towaru)

Modle Wymiany jest w równowadze gdy ceny p^* są takie, że popyt jest

zaspokojony czyli

Takie ceny p^* to ceny równowagi.

Założenie: Prawo Warlasa

Dla dowolnych cen niezerowych

Wartość nadwyżki popytu p*g(p) jest zerowe nie tylko w równowadze.

Gdy
to prawo Warlasa jest spełnione

Spostrzeżenie g(p)=g(αp) α > 0

Uzasadnienie:

więc dⁱ(p) =dⁱ(α p) i d(p) =d(α p)

Jeżeli
jest cena równowagi to dla k α > 0

α p jest też ceną równowagi.

WYKŁAD IV 20.12.2003 r.

PRAWO WARLASA

Przeliczenie wszystkiego na jeden towar (jednostką jest towar za towar).

Gdy mamy ceny
trzech towarów jeżeli pomnożymy przez to α p jednostki

Pozostaną te same to nowe ceny powstaną z podziału przez np.: pierwszy towar.

np.: gdy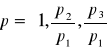

(jednostka rozliczeniowa jeden towar np.: p₁

Ujednoznacznienie cen:

Warlas: Jeden z towarów pełni rolę jednostki rozliczeniowej („numeraive”) jego cena jest zawsze =1.

Np.: Gdy nie doszło do wymiany towaru bo wszyscy maja ten sam towar to cena 1-wszego towaru jest nieokreślona wówczas

Gdy np.: jest to pierwszy towar to zamiast cen p rozpatrujemy „nowe” ceny

Ale p₁ może być =0!

Lepiej ograniczyć inaczej przestrzeń cen np. wybierając za jednostkę rozliczeniową zamiast ustalonego towaru zestaw towarów zawierający po jednostce każdego towaru prowadzi to do opisanej dalej normalizacji cen

p = (p₁, p₂, p₃)

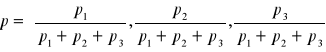
zawartość całego koszyka

Wyróżniamy wszystko w jednostce rozliczeniowej (koszyk cały) czyli:

p = |p₁, p₂,…, p_n|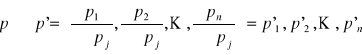

gdzie

Zbiór wszystkich cen niezerowych, które spełniają warunek w sumie dają liczbę 1 (ceny znormalizowane)

p≥ 0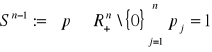
- przestrzeń cen znormalizowanych

przestrzeń cen znormalizowanych synteks

ilość towarów (koszyka) w stosunku wymiernym

cena cena znormalizowana

p = (p₁, p₂₎

p₂

p n=2

S¹

p'

1

1 p₁

p₁ S²

1

p

p'

1 p₂

1

Istnienie (cen równowagi)

Podsumowanie zagadnienia:

a)
- ciągła

b) g s-nia prawo Warlasa p ∈ S^n-1 pg (p)0

c) szukany

(nie prawda g(p) ≤ 0 ∃! : g_j(p) < 0)

_ +

pg (p) = 0 ∃_{k j} g_k (p) < 0

• popyt na j-ty towar nie jest zaspokojony

• na k-ty towar występuje nadwyżka podaży

modyfikacja ceny: p_j - zwiększa, p_k - zmniejsza

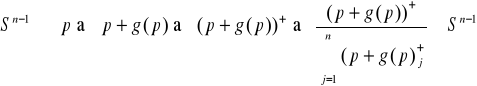
np.

g(p) = (1,-2,0)

p = 1/10(6,3,1)

(16/10, -17/10, 1/10)

nie powinno być ujemnej wartości zamieniamy ją na 0

(16/10, 0, 1/10)

10/17*(16/10, 0, 1/10) = (16/17, 0, 1/17)∈ S^n-1

wektor cen znormalizowanych

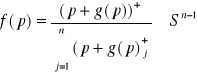
p=f(p) ?

p∈ S^n-1 X

x f(x)

f : X X

x ∈ X

f(x) = x

TWIERDZENIE Funkcja f jest dobrze zdefiniowana odtworzeniem S^n-1 S^n-1 jest ciągła,

Której punkt stały tej funkcji to cena równowagi.

TWIERDZENIE (Brouwer1910) Każda funkcja ciągła S^n-1 S^n-1 ma punkty stałe.

Warunek. Dla modelu wymiany spełniającego postanowienia założenia, istnieją ceny równowagi.

K. Przyłuski -EKONOMIA MATEMATYCZNA

- 1 -

względna zmiana popytu

względna zmiana ceny

[bezwzględna] zmiana f(x)

[bezwzględna] zmiana x

względna zmiana f(x)

względna zmiana x

η%f(x) ξ%x

f(x) x

f(x)

max globalne

x (argumenty)

Poziom produkcji gdy zysk=0

q_b

Π(q)

q

Π(q)

q

-

+

q_b

Π(q)

q

-

+

q_s

D(p)

2

2=D(p)

Dla tej ilości ∃! (istnieje dokładnie jedna) cena p taka, że q=D(p)- wartość popytu jednej ceny

(pole prostokąta)

q

p

x

I x

X₂

X₁

Rⁿ₊

y ≻ x

1.

I x

X₂

X₁

Rⁿ₊

y x

2.

(łącznie z krzywą)

I x

X₂

X₁

Rⁿ₊

y x

3.

X₁

0 1 2 3 4

X₂

4

3

2

1

Wzrost preferencji konsumenta

X₁

0 1 2 3

X₂

4

3

2

1

Wzrost preferencji konsumenta

1:1

X₁

0 1 2 3

X₂

4

3

2

1

Wzrost preferencji konsumenta

1:2

X₂

X₁

0 1 2 3

3

2

1

Wzrost preferencji konsumenta

1:1

1:2

X₂

X₁

0 1 2 3

4

3

2

1

Wzrost preferencji konsumenta

1:1

X₂

X₁

Punkt nasycenia

0

X₂

X₁

y ≥ x

Rⁿ₊

Monotoniczność

X₂

X₁

0

y ≠ x & y ≥ x

Ścisła monotoniczność

x

X₂

X₁

0

Monotoniczność

y ≥ x

x

X₂

X₁

0

Ścisła monotoniczność

y ≠ x & y ≥ x

y

xx +(1-x)

y

x

x∈ [0, 1]

Jeśli x =1 p =x

Jeśli x =0 p =y

x

x∈ (0, 1)

Ix

xy +(1-x) z

z

y

x

Rⁿ₊

Nie jest ściśle wypukła

x

2

0 1 2

y

x

2

1

2

1

y

x

0 1 2

Preferowane bardziej

X

z

x

x y

Ix

y x

-β

-β

β

β

ilość drugiego towaru

---