Wyrównanie poziome ciągu tachimetrycznego

A, B - punkty osnowy geodezyjnej,

,
- 'zmierzone' odległości poziome;
,
- błędy średnie pomiarów odległości

,
- 'zmierzone' kierunki;
,
- błędy średnie pomiarów kierunków

Przyrosty współrzędnych:
;
;
;

Przybliżone wartości odległości:
;

Przybliżone wartości azymutów:
;

Przybliżona wartość
azymutu zera koła poziomego
- stała orientacyjna tachimetru

jest obliczana na podstawie pierwszego zmierzonego kierunku
.

Przybliżone wartości kierunków:
;
.

Linearyzacja równań

Wyprowadzenie równania poprawki azymutu

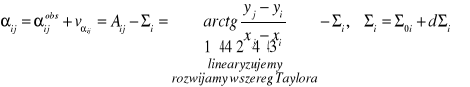
Linearyzacja

.

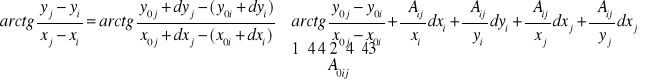
Stąd

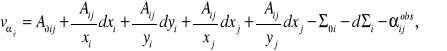
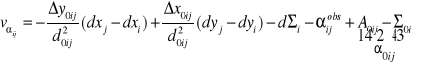
- przybliżona wartość mierzonego kierunku.

Stąd

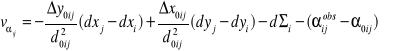
Pochodne cząstkowe

otrzymujemy różniczkując funkcje azymutu. Przykładowo

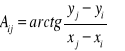
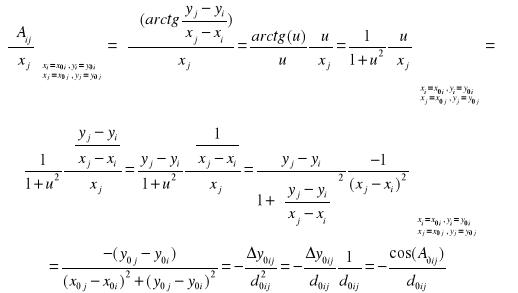
Wyprowadzenie równania poprawki odległości

Linearyzacja

,

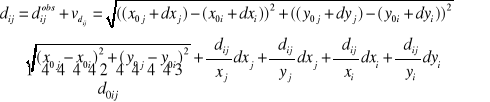
Stad

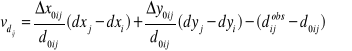
Pochodne
itp. obliczane są w punkcie
:

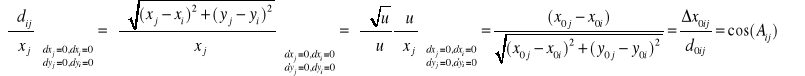
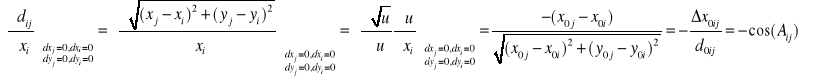
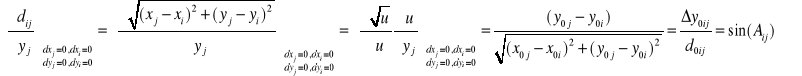
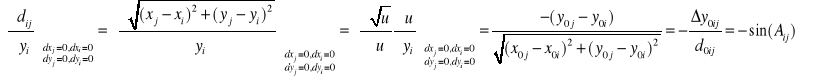
Wzorce równań poprawek odległości i azymutu

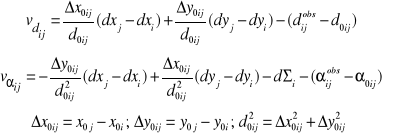
Korzystając z wzorców układamy (odpowiadający oznaczeniom rysunku) układ równań poprawek

Ponieważ punkty A i B są stałe (dokładne), to
, to

Wynikiem rozwiązania tego układu powinny być wielkości wyrównane

Układ ten (w celu uproszczenia oznaczeń) można przepisać następująco

,
.

Postać macierzowa

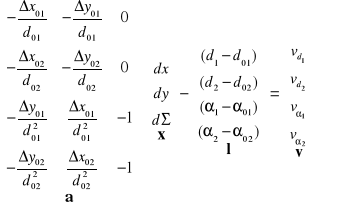
x - wektor niewiadomych, a - macierz układu równań poprawek, l - wektor wyrazów wolnych.

Macierz błędu obserwacji C, macierz wag p

,

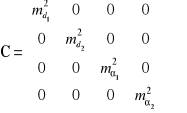
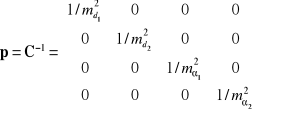
Układ obserwacyjny

.

Rozwiązanie układu - metoda najmniejszych kwadratów

Układ równań poprawek rozwiązywany jest metodą najmniejszych kwadratów

Macierz
jest symetryczną macierzą współczynników układu równań normalnych:

Formalne rozwiązanie (metoda Gaussa, Banachiewicza itp.) tego układu można zapisać w postaci:

Rozwiązanie
określają współrzędne stanowiska x, y i stałą orientacyjną
:

,
,

Błędy współrzędnych i stałej orientacyjnej

,

,
,
.

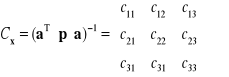
Poprawki

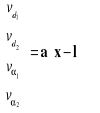
Obserwacje wyrównane

,
,

Błędy obserwacji wyrównanych

,
,
,

- kolejne wiersze macierzy układu równań poprawek
, odpowiadające kolejnym obserwacjom. Są to wektory gradientów odległości i azymutów wyznaczonych na podstawie wyznaczonych współrzędnych przybliżonych.

Błędy poprawek obserwacji

,
,

,
,

Warunki poprawności wyrównania

Wyrównane współrzędne punktów, odległości i kierunki są poprawne jeśli

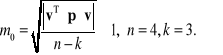
Równanie poprawki kątowej

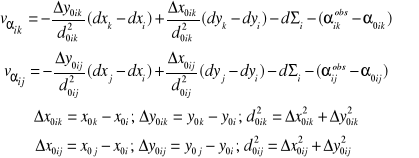
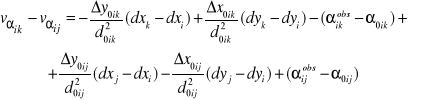
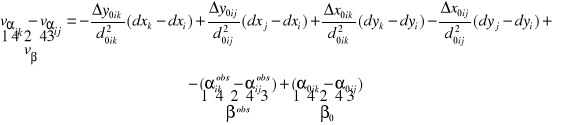
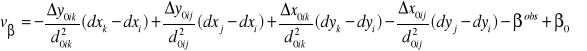
Układ równań poprawek - równań obserwacyjnych w ujęciu macierzowym

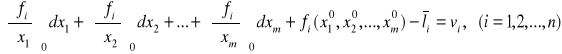
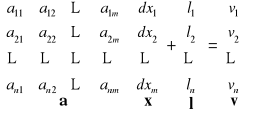
Układ równań normalnych

Układ ten wynika z warunku:

,

mówiącego, że suma kwadratów poprawek pomnożona przez współczynniki wag jest minimalna. Zauważmy, że
jest funkcją skalarną, której argumentami są składowe wektora

Minimum tej sumy wyznacza się wykorzystując zależności:

W zapisie wykorzystano (skrótową) notację różniczkowania wektorowego. Symbol
oznacza, że należy wyznaczyć pochodne cząstkowe wyrażenia
kolejno względem wszystkich argumentów
tj. składowych wektora x. Takie zależności znacznie upraszczają prowadzenie przekształceń.

Transponując
otrzymuje się zależność
. Ponieważ z układu poprawek:
to:

Otrzymane wyrażenie nazywa się układem równań normalnych. Rozwiązanie tego układu
dane jest zależnością:

Z postaci tego rozwiązania wynika, że jest ono wektorem, którego składowe są liniowymi funkcjami składowych wektora pomiarów L.

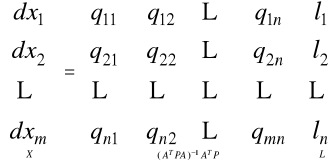
Analogicznie dla wektora poprawek:

Wykazano, że wektor rozwiązań X i poprawek V są funkcjami składowych wektora pomiarów L. Można, więc wyznaczyć ich macierze kowariancyjne.

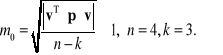
Transponowanie iloczynu macierzy

8

Cel - B

0

(x₀, y₀)

Cel - A

0

Azymut kierunku zera koła poziomego

Azymuty mierzonych

kierunków

Układ równań poprawek

Cel - A

(x, y)

wyrównane współrzędne stanowiska tachimetru S

y

Cel - B

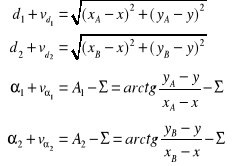
S

d₂

d₁

k

A

S

- przybliżone współrzędne stanowiska tachimetru

d

y

B

i

0

Współrzędne przybliżone

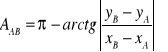
d₂

Wyznaczenie współrzędnych przybliżonych

d₁

j

Zero koła poziomego

Wyrównane współrzędne (x, y) stanowiska tachimetru S można wyznaczyć rozwiązując powyższy nieliniowy układ równań poprawek odległości d₁, d₂ i kierunków α₁, α₂

Celem wyrównania obserwacji jest wyznaczenie poprawek
,
do obserwowanych odległości
i kierunków
. Wskaźniki i oznaczają stanowiska tachimetru, j - widoczne ze stanowisk cele.

wyrównane współrzędne i -tego stanowiska tachimetru,
współrzędne przybliżone, poszukiwane przyrosty

y

0

Azymut kierunku zera koła poziomego - stała orientacyjna tachimetru

Azymut

mierzonego

kierunku

(x_A, y_A)

S

d₂

d₁

(x_B, y_B)

j - Cel

i

Stanowisko tachimetru

- wyrównane współrzędne i -tego stanowiska tachimetru

1

Równania poprawek linearyzujemy rozwijając je w ucięty szereg Taylora względem przyrostów
.

;

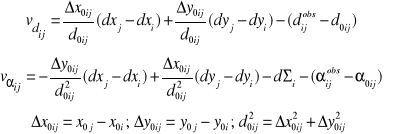
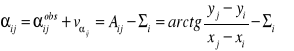
Wzory równań poprawek odległości i azymutu

Równania poprawek

---