5EKRAN_185

Lekcja 8

Pole magnetyczne

Poniżej przedstawione zostaną podstawowe własności pola magnetycznego prowadzące do praw w obwodach magnetycznych. Zaprezentowano zostaną przykłady obliczeniowe charakteryzujące się symetrią pozwalającą na zastosowanie prawa Ampera.. Przedstawiono również analizę magnetowodu na przykładzie tzw. zagadnienia prostego.

.

5EKRAN_186

W wielu urządzeniach przemysłowych występujące pole magnetyczne ma charakter wolnozmienny. Zmianie pola magnetycznego towarzyszy indukowanie się pola elektrycznego, co w pełnej formie opisują równania Maxwella. Jednak z punktu widzenia inżynierskiego wyniki otrzymane dla pola magnetycznego stałego w czasie znajdują zastosowanie w przypadku pól wolnozmiennych.

5EKRAN_187

Źródła pola magnetycznego: magnesy trwałe, przewody z prądem.

Komentarz-EKRAN_187

Pole magnetyczne stacjonarne inaczej pole magnetostatyczne to pole stałe w czasie często nazywane wprost polem magnetycznym.

5EKRAN_188

Podstawowa wielkość charakteryzująca pole magnetyczne to natężenie pola magnetycznego
. H - wielkość wektorowa, wyznacza się na podstawie reguły śruby prawoskrętnej, reguły prawej dłoni.

Strumień magnetyczny w rdzeniu

Komentarz-EKRAN_188

Linie pola magnetycznego przenikające pewną powierzchnię nazywamy strumieniem magnetycznym.

5EKRAN_189

Indukcja magnetyczna -wielkość określająca pole magnetyczne w danym środowisku:

gdzie: 1H(henr)=1Ω 1s

μ_r - przenikalność względna(wielkość bezwymiarowa) magnetyczna ośrodka (środowiska)

μ_rμ₀=μ - przenikalność magnetyczna środowiska

1T(tesla) - jednostka indukcji magnetycznej

gdzie:

Komentarz-EKRAN_189

Inną wielkością charakteryzującą środowisko ze względu na właściwości magnetyczne jest wektor polaryzacji magnetycznej :

Wektor ten określa zdolność materiału do magnesowania pod wpływem zewnętrznego pola magnetycznego o natężeniu H

χ - podatność magnetyczna

5EKRAN_190

φ - strumień indukcji magnetycznej :φ[Wb]

W ogólnym przypadku strumień magnetyczny określany jest przez wzór:

Strumień magnetyczny przez powierzchnię

Komentarz-EKRAN_190

Wyrażenie pod całką jest iloczynem skalarnym wektora indukcji oraz wektora prostopadłego do rozpatrywanej powierzchi. W przypadku, gdy rozpatrujemy strumień pola jednorodnego

czyli
to

5EKRAN_191

Prawo Gaussa

Całkowity strumień wektora indukcji wypływający na zewnątrz dowolnej powierzchni zamkniętej S równy jest zero - bezźródłowość pola magnetycznego.

Prawo Gaussa - I prawo Kirchoffa dla obwodów magnetycznych:

Komentarz-EKRAN_191

Analogicznie jak w teorii obwodów na podstawie prawa Gaussa wyprowadza się I prawo Kirchhoffa dla strumieni magnetycznych.

Pierwsze prawo Kirhhoffa dla obwodu magnetycznego

5EKRAN_192

Prawo Biota - Savarta

Prawo Biota-Savarta określa wartość i zwrot natężenia dH pola pochodzącego od elementarnego fragmentu przewodu dl, przez który płynie prąd:

Rys.10.5. Prawo Biota-Savarta

Komentarz-EKRAN_192

Z iloczynu dl
r wynika, że wektor dH jest w płaszczyźnie prostopadłej do przewodnika. Wartosć skalarna wektora dH wynosi:

gdzie:

5EKRAN_193

Prawo Biota - Savarta - zastosowanie.

Przykład

Oblicz wartość natężenia pola w środku okręgu wiodącego prąd.

Pole magnetyczne wokół przewodnika kołowego

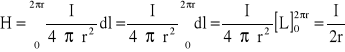
Komentarz-EKRAN_193

Pole magnetyczna od każdego elementarnego odcinka dl zwoju kolowego jest prostopadłe do jego powierzchni. Stąd dodawanie elementarnych indukcji dB można przeprowadzić z zastosowaniem całki (skalarnie).

5EKRAN_194

Prawo przepływu.

Całka liniowa natężenia pola magnetycznego H po dowolnym konturze zamkniętym L jest równa sumie strug prądowych przenikających przez dowolną powierzchnię S rozpiętą na tym konturze.

- przepływ (wirowość pola magnetycznego)

Strugi prądowe przenikające powierzchnię rozpiętą na konturze s

Komentarz-EKRAN_194

Przepływ Θ często nazywany jest także amperozwojami lub siłą magnetomotoryczną. Przy wyznaczaniu przepływu istotny jest zwrot prądu. Jeżeli jest on zgodny ze zwrotem wynikającym z reguły śruby prawoskrętnej dla zastrzałkowanego wektora natężenia pola to w równaniu piszemy go z plusem w przeciwnym przypadku z minusem

Θ= I₁+I₂+I₃+I₄

5EKRAN_195

Przepływ w przypadku strug wiodących jednakowy prąd (amperozwoje)

Komentarz-EKRAN_195

W przypadku gdy daną powierzchnię przebija przewód wiodący ten sam prąd na przykład z razy to przepływ określa iloczyn liczby zwojów i prądu. Sytuacja ta miejsce w przypadku wyznaczania przepływu cewki.

5EKRAN_196

Zastosowanie prawa przepływu:

Przykład

Obliczyć natężenie pola magnetycznego w funkcji r wokół nieskończenie długiego przewodnika wiodącego prąd:

Pole magnetyczne wokół nieskończenie długiego przewodnika

Komentarz-EKRAN_196

Prawo Ampera najczęściej stosujemy w przypadku gdy widoczna jest symetria pola. W rozpatrywanym przypadku zakładamy, że natężenie pola w danej odległosci r musi być jednakowe. Zatem wybierając drogę po okręgu będziemy przyjmować, że wzdłuż niej natężenie pola jest stałe.

5EKRAN_197

Rozwiązanie

ponieważ H=const (dla r = r_x) oraz wektory H i dl są w każdym punkcie konturu L równoległe stąd:

czyli:

Komentarz-EKRAN_197

Ze względu na to, że wybraną powierzchnię o promieniu r przebija jeden zwój to prąd, który on przewodzi stanowi amperozwoje w prawie Ampera.

5EKRAN_198

Przykład

Określić rozkład pola magnetycznego w przewodniku przy założeniu stałej gęstości prądu w przewodzie.

- gestość średnia prądu

Prąd zawarty w powierzchni
(r < r₀) będzie miał zatem wartość:

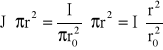
Przekrój przewodnika kołowego

Komentarz-EKRAN_198

Dzieląc prąc całkowity przez przekrój przewodu wyznaczamy gęstośc prądu stałego lub średnią gęstość w przypadku prądu zmiennego.

5EKRAN_199

Ze względu na to, że wzdłuż konturu kołowego o promieniu r H=const. z prawa przepływu mamy:

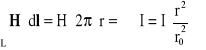
1⁰


(funkcja liniowa)

2⁰ r > r₀
(hiperbola)

Rozkład pola w przewodniku przy stałej gęstości prądu

Komentarz-EKRAN_199

Podobnie jak w poprzednim przypadku wykorzystujemy symetrię pola magnetycznego zarówno na zewnątrz przewodnika jak i wewnątrz. Do określenia przepływu wewnątrz przewodnika posługujemy się gęstością prądu. Jak widać z wykresu natężenia pola magnetycznego w funkcji odległości od jego środka wartość maksymalną natężenie przyjmuje na powierzchni przewodnika.

Należy podkreślić, że rozwiązanie otrzymano przy założeniu stałej gęstości prądu. Założenie to jest uprawnione dla prądów stałych i wolnozmiennych. Należy przy tym pamiętać, że w przypadku prądów o znacznej częstotliwości ujawnia się zjawisko wypierania prądu na zewnątrz przewodnika.

5EKRAN_200

Działania dynamiczne w polu magnetycznym.

Siłę działającą na przewodnik z prądem znajdujący się w polu magnetycznym określa
prawo Laplace'a:

dF= I∙(dl×B)

Wartość elementarnej siły

Prawo Laplace'a

Komentarz-EKRAN_199

Jeżeli przewodnik z prądem znajdzie się w polu magnetycznym to na każdy element tego przewodnika działa siła. Zwrot siły można wyznaczyć stosując regułę lewej dłoni. Lewą dłoń ustawiamy tak aby pole wbijało się w nią prostopadle, jednocześnie palce wskazują kierunek prądu, wówczas wyprostowany kciuk wskaże nam zwrot siły. W ogólnym przypadku kierunek i zwrot siły wyznacza iloczyn wektorowy dlxdB.

5EKRAN_201

Przykład

Wyznaczyć siłę oddziaływania pomiędzy dwoma równoległymi przewodnikami o nieskończonej długości wiodącymi prąd.

Siła oddziaływania przewodów pomiędzy nieskończenie długimi przewodnikami z prądem

Komentarz-EKRAN_201

Wykorzystując wzór na pole wokół nieskończenie długiego przewodnika wiodącego prąd można wyznaczyć siłę oddziaływania pomiędzy dwoma równoległymi przewodnikami. Jeżeli prądy płyną w tym samym kierunku to przewodniki przyciągają się.

5EKRAN_202

Wychodząc z prawa Laplace'a można określić siłę działającą na cząstkę o ładunku q:

ponieważ

stąd:

gdzie:
- prędkość ładunków

Ostatecznie siła działająca na poruszający się w polu magnetycznym ładunek q wynosi:

Komentarz-EKRAN_202

Jeżeli uwzględnimy siłę działającą na ładunek q w polu elektrycznym o natężeniu E wynoszącą:
to otrzymamy:

Poruszający się ładunek pod wpływem B wywołuje E.

5EKRAN_203

Podział ciał ze względu na właściwości magnetyczne:

1. Diamagnetyki
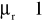
   (μ_r<1 nieznacznie) miedź, cynk, srebro, złoto

2. Paramagnetyki μ_r>1 aluminium, cyna, platyna

3. Ferromagnetyki μ_r>>1

Charakterystyki B=f(H) ciał 1) i 2) są liniowe.

Charakterystyka magnesowania ferromagnetyka

Komentarz-EKRAN_203

B_r - indukcja szczątkowa

H_k - natężenie koercji

Ferromagnetyki miękkie charakteryzują się wąską pętlą histerezy

Ferromagnetyki twarde - szeroką pętlą histerezy

5EKRAN_204

Charakterystyka średnia

Wyznaczenie charakterystyki średniej

Komentarz-EKRAN_204

Do obliczeń z materiałami miękkimi i w magnetowodach, gdzie prąd do określonej wartości zmierzał jednokierunkowo wykorzystuje się charakterystykę pierwotną lub średnią. Określenie charakterystyki średniej polega na wyznaczeniu rodziny histerez, dla których tworzy się linię łączącą ich wierzchołki.

5EKRAN_205

Średnia (pierwotna) charakterystyka magnesowania

Komentarz-EKRAN_205

Fragment charakterystyki od początku układu do punktu A - nazywamy zakresem liniowości.

Dalszy fragment nie można byłoby nazwać liniowym, wreszcie od punktu B mówimy, że charakterystyka przechodzi w stan nasycenia.

5EKRAN_206

Przenikalność magnetyczna statyczna i dynamiczna:

Przenikalność magnetyczna statyczna i dynamiczna

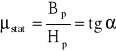
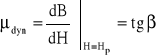
Komentarz-EKRAN_206

Podobnie jak w przypadku rezystancji w obwodach nieliniowych, określana jest magnetyczna przenikalność statyczna w danym punkcie charakterystyki (tangens kąta nachylenia siecznej) oraz dynamiczna (tangens kąta stycznej) w danym punkcie pracy.

5EKRAN_207

Pole magnetyczne w toroidzie

Toroid

Komentarz-EKRAN_207

Zwróćmy uwagę, że na drodze L₁ H=const. Natomiast powierzchnię określoną przez koło L₁ uzwojenie wiodące prąd I przebija z-krotnie.

5EKRAN_208

z - liczba zwojów czyli w toroidzie :

Rozkład ntężenia pola w toroidzie

Jeżeli μ=const to

Komentarz-EKRAN_208

Z rozkładu natężenia pola w toroidzie wynika, że pole w całym przekroju magnetowodu nie jest stałe. Z drugiej strony wygodnie jest przyjąć wartość średnią natężenia pola określoną dla tzw. średniej drogi geometrycznej w magnetowodzie. Wówczas przy analizie magnetowodów dzieląc strumień przez przekrój otrzymamy indukcję, która będzie odpowiadała wartości średniej.

5EKRAN_209

Napięcie magnetyczne

Definicja napięcia magnetycznego:

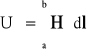
Jeżeli na drodze l H=const
to U_m=Hl=H_śrl_śr

Komentarz-EKRAN_209

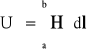
nazywamy napięciem magnetycznym pomimo wymiaru ampera poprzez porównanie z definicją napięcia w polu elektrycznym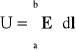

5EKRAN_210

Komentarz-EKRAN_210

Wielkości i prawa obwodów magnetycznych można przez analogie porównać do obwodów prądu stałego, stąd obwód magnetyczny często rysujemy w postaci zastępczego schematu elektrycznego.

5EKRAN_211

Obwodowy schemat zastępczy magnetowodu

Schemat zastępczy obwodu magnetycznego

Komentarz-EKRAN_211

Uwzględniając analogie pomiędzy obwodem magnetycznym a elektrycznym, w dalszym ciągu będziemy zakładali, że strumień pola magnetycznego w danej gałęzi obwodu magnetycznego jest stały. Z kolei fragment magnetowodu może być reprezentowany przez jeden dwójnik o pewnej reluktancji lub napięciu magnetycznym H_kl_i jeżeli stanowi jednorodny materiał o stałym przekroju. W innym przypadku gałąź będzie zawierała odpowiednią liczbę szeregowo połączonych elementów.

5EKRAN_212

Prawa obwodów magnetycznych

II prawo Kirchhoffa dla obwodów magnetycznych-

I prawo Kirchhoffa dla obwodów magnetycznych-

Prawo Ohma

przyjmujemy że H=const

- reluktancja drogi magnetycznej

- permeancja

Komentarz-EKRAN_212

Porównując wzór na rezystancję przewodu o pewnej długości, przekroju i przewodności właściwej, który ma postać:
stwierdzamy analogię z reluktancją magnetyczną. Z kolei odwrotność reluktancji zwana permeancją jest wielkością analogiczną do konduktancji.

9EKRAN_223

Lekcja 9- Prawo Faradaya

Lekcja 9 jest kontynuacją zagadnień związanych z prawami i własnościami pola magnetycznego. W lekcji tej czytelnik pozna jedno z ważniejszych praw magnetyzmu - prawo Faradaya. Z prawem tym związana jest tzw. reguła Lenza pozwalająca na określanie zwrotów wyznaczanych wielkości. Zdefiniowano następny element obwodu jakim jest cewka oraz jej charakterystyczną wielkość- indukcyjność własną.

9EKRAN_224

Indukcja elektromagnetyczna.

Zjawisko indukcji elektromagnetycznej polega na indukowaniu siły elektromotorycznej przy zmianach strumienia magnetycznego.

Prawo Faradaya

-strumień sprzężony

Komentarz-EKRAN_224

Podana tu definicja strumienia sprzężonego jest prawdziwa jeżeli strumień wytwarzany przez każdy zwój przenika wszystkie pozostałe ( nie ulega rozproszeniu).

9EKRAN_225

Reguła Lenza

Każda zmiana strumienia powoduje wyindukowanie siły elektromotorycznej o takim kierunku by prąd płynący pod jej wpływem wywołał strumień przeciwdziałający pierwotnej zmianie strumienia.

a)

Komentarz-EKRAN_225

W zależności od sposobu zastrzałkowania można przyjąć we wzorze Faradaya znak plus lub minus. W przypadku a) jeżeli magnes porusza się w lewo czyli strumień  narasta to pochodna ma znak dodatni i siła elektromotoryczna generuje strumień o przeciwnym zwrocie (przeciwdziałanie zgodnie z regułą Lenza). Z kolei jeżeli magnes zacznie poruszać się w prawo strumień zacznie maleć (pochodna ujemna) co oznacza, że zmieni się zwrot SEM a stąd zwrot _d ) przeciwdziałanie zostanie zachowane).

9EKRAN_226

b)

Komentarz-EKRAN_226

Ponieważ w każdym z przypadków a i b przy poruszaniu się magnesu zgodnie z zastrzałkowaną prędkością v strumień narastał (czyli jego pochodna była dodatnia) stąd strumień _d przeciwdziałający musi mieć rzeczywisty zwrot przeciwny do , a taki wywoła zwrot prądu wymuszony zwrotem SEM jak na rys. a. Zastrzałkowanie prawoskrętne (rys.b) musi oznaczać że wartości e,i,_d<0

W dalszym ciągu będziemy przyjmowali lewoskrętne strzałkowanie SEM względem strumienia wzbudzającego tą SEM.

9EKRAN_227

Rozważmy z kolei dwie cewki nawinięte różnie na rdzeń, oraz rozpatrzmy zjawisko zachodzące w czasie I ćwiartki prądu sinusoidalnego. (przebieg sinusoidalny prądu poniżej)

a) prawoskrętnie nawinięta cewka

b) lewoskrętnie nawinięta

Komentarz-EKRAN_227

Z rysunków a) i b) wynika, że bez względu na sposób nawinięcia cewek można przyjąć (przy lewostronnym strzałkowaniu SEM względem strumienia _d) odbiornikowy sposób strzałkowania prądu i napięcia.

Łatwo wykazać, że wzór
jest poprawny dla odbiornikowego strzałkowania cewki dla pozostałych ćwiartek.

.

I

S

N

N

S

N

S



B

dS

.

α

α

S₁

S₂

S₃

dS

B₁

dS

dS

B₂

B₃

i

V

N

S

e

_d

r

dH

I

I

I

I

i(t)

I

r

r₀

H_max

H

r

r₀

i

e

e

e

i(t)



_d

e

H_k

B_r

B

H

-B_r

-H_k

charakterystyka pierwotna

H

B

B

A

B

H

B

H

H_p

B_p

α

β

D

C

B

A

φ₂

φ₁

φ₃

φ₄

φ₅

φ₆

φ₇

φ₈

I₁

Z₁

I₂ Z₂

I₂Z₂

φ₁

I₁Z₁

H₄l₄

φ₂

H₂l₂

H₃l₃

H₁l₁

φ₅

φ₈

φ₃

φ₄

φ₆

φ₇

t



i

V

N

S

strzałkowanie

lewoskrętne względem strumienia wzbudzającego

IV

B

III

dl

I

II

e

_d

i

i(t)

e

t



Θ = Iz





e

_d

strzałkowanie

prawoskrętne

---