Sprawozdanie nr 5 z laboratoriów systemów przetwarzania sygnałów
Temat: Funkcja splotu i jej własności. Obcinanie funkcji sinc jako wstęp do filtrów. Zastosowanie okien do utworzenia filtru dolno przepustowego. Podstawowe rodzaje filtrów
Grupa : IZ38-I	Data: 02.06.08
Wykonał: Jerzy Myc	Ocena:

Zadania:

1. Laboratorium 1 - Zbadać własności splotu

1. Przemienność
   

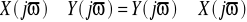
2. Łączność
   

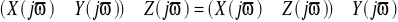
3. Rozdzielność
   

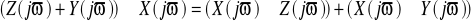
2. Laboratorium 2 - Obcinanie funkcji sinc i badanie jej za pomocą FFT :

1. Wycinając symetryczny odcinek ze środka funkcji sinc

2. Wycinając niesymetryczny odcinek ze środka funkcji sin

3. Laboratorium 3 - Filtry:

1. Zbadać właściwości różnych okien dla symetrycznego kawałka funkcji sinc

2. Przefiltrować przy pomocy powstałego filtru szum biały

Laboratorium 1 - Splot :

a). Przemienność

Do tego zadania wykorzystałem funkcję sinusoidalna złożoną z 3 sinusów (out 2) oraz szum biały (out 1).

Wniosek :

Patrząc na końcowe wykresy widać iż przemienność splotu jest spełniona, gdyż wykresy są identyczne.

b). Łączność

Do tego zadania wykorzystałem funkcję sinusoidalna złożoną z 3 sinusów(out 3) , szum biały(out 1) i funkcje kwadratową (out 2)

Wniosek :

Patrząc na końcowe wykresy widać iż łączność splotu jest spełniona, gdyż wykresy są identyczne.

c). Rozdzielność:

Do tego zadania wykorzystałem funkcję sinusoidalna złożoną z 3 sinusów(out 3) , szum biały(out 1) i funkcje kwadratową (out 2)

Wniosek:

Patrząc na końcowe wykresy widać iż rozdzielność splotu jest spełniona, gdyż wykresy są identyczne.

Laboratorium 2 - Obcinanie funkcji sinc :

a). Układ do badania

Function SINC:

Ustawiłem funkcje sinc tak aby znajdowała ona się dokładnie po środku czasu symulacji. Następnie zauważyłem że w 1000 próbek wartość równą 1 przyjmuje w elemencie 501 . Postanowiłem więc zbadać funkcję dla robiąc symetryczną próbkę względem środka i niesymetryczna (od punktu gdzie wartość równa jeden do konkretnej wartości).

b). Obcinanie równomierne:

3 symetryczne próbki:

23 symetryczne próbki:

203 symetryczne próbki:

Wnioski:

Zwiększenie ilości próbek powoduje wyostrzenie charakterystyki częstotliwościowej . Przy trzech próbkach jest to łagodny spadek. Zwiększając liczbę próbek , zwiększamy liczbe zafalowań oraz zaostrzamy spad. Widać to także na wykresie fazowym gdzie faza zmienia się coraz szybciej wraz ze wzrostem liczby próbek symetrycznych.

c). Obcinanie nierównomierne:

3 niesymetryczne próbki:

11 niesymetrycznych próbek:

101 niesymetrycznych próbek:

Wnioski:

Zwiększenie ilości próbek powoduje wyostrzenie charakterystyki częstotliwościowej . Lecz nie w taki sposób jak przy próbce symetrycznej. Spadek wyostrza się ale nie w takim stopniu jak przy symetrycznej próbce. Natomiast charakterystyka fazowa jest łagodniejsza niż w poprzednim podpunkcie. Oraz różnica pomiędzy poziomem niskim jest mniejsza niż w przypadku próbki symetrycznej.

Laboratorium 3 - Tworzenie filtra :

Do badania okien i splotu z szumem użyłem następującego układu:

OKNA:

1. Bartleta

2. Blackman

3. Boxcar

4. Chebyshev

5. Hamming

6. Hann

7. Hanning

8. Kreiser

9. Triag

Wnioski

Filtr	Pasmo przepustowe	Pasmo Zaporowe	Przejście
Bartleta	0-0.27 kHz	Od 0.5 kHz	0.28-0.49 kHz
Blackman	0-0.27 kHz	Od 0.48 kHz	0.28-0.47 kHz
Boxcar	0-0.27 kHz	Od 0.46 kHz	0.28-0.45 kHz
Chebyshev	0-0.27 kHz	Od 0.5 kHz	0.28-0.49 kHz
Hamming	0-0.28 kHz	Od 0.48 kHz	0.29-0.47 kHz
Hann	0-0.27 kHz	Od 0.48 kHz	0.28-0.47 kHz
Kreiser	0-0.25 kHz	Od 0.46 kHz	0.26-0.45 kHz
Triag	0-0.3 kHz	Od 0.5 kHz	0.3-0.49 kHz

SPLOT Z WHITE BANDWITH NOISE:

1. Triag

2. Bartleta

3. Kreiser

Wniosek

Splot filtru z szumem białym powoduje iż częstotliwości wyższe są obcinane. W zależności od typu okna, zmniejszanie amplitud jest mniej lub bardziej gwałtowne.

---