zad.1

Obliczyć wartość wyznacznika macierzy współczynników podanego równania, podać wartość elementu
macierzy odwrotnej do macierzy współczynników, rozwiązać podany układ równań:

>> a=[7.9 5.6 5.7 -7.2;8.5 4.8 .8 3.5;4.3 4.2 -3.2 9.3;3.2 -1.4 -8.9 3.3]

a =

Columns 1 through 3

7.9000 5.6000 5.7000

8.5000 4.8000 0.8000

4.3000 4.2000 -3.2000

3.2000 -1.4000 -8.9000

Column 4

-7.2000

3.5000

9.3000

3.3000

>> b=[6.68 9.95 8.6 1]'

b =

6.6800

9.9500

8.6000

1.0000

wyz=det(a)

wyz = -1.911769600000000e+003

>> x=a^(-1)*b

x =

0.6208

0.6644

0.1508

0.3895

>> odw=inv(a);

>> el=odw(3,4)

el =

-0.1205

zad. 2

Znaleźć miejsca zerowe wielomianu:

>> clear x

>> x=roots([1 0 0 -1 -1])

x =

1.2207

-0.2481 + 1.0340i

-0.2481 - 1.0340i

-0.7245

zad. 3

Znaleźć pierwiastek równania:

x=subs(solve('x^4-10*x^3+1','x'))

x =

9.9990

0.4717

-0.2353 + 0.3958i

-0.2353 - 0.3958i

ezplot('x^2+1/x^2-10*x',[.2 12]);grid;

>> x1=fzero('x^2+1/x^2-10*x',.4)

x1 =

0.4717

>> x1=fzero('x^2+1/x^2-10*x',9)

x1 =

9.9990

zad.4

Utworzyć tabelę wartości funkcji:

i narysować jej wykres w przedziale [,2] (dla 51 wartości zmiennej niezależnej ).

>> x=linspace(pi,2*pi,51);

>> y=x.^2.*exp(-2*x)./(2*x.^3+3);

>> tabl=[x' y'];

>> plot(x,y)

>>

zad.5

Znaleźć całkę:

>> syms x

> v=int(x*exp(x^(1/3)),x)

v =

3*x^(5/3)*exp(x^(1/3))-15*x^(4/3)*exp(x^(1/3))+60*x*exp(x^(1/3))-180*x^(2/3)*exp(x^(1/3))+360*x^(1/3)*exp(x^(1/3))-360*exp(x^(1/3))

pretty(v)

5/3 1/3 4/3 1/3 1/3 2/3 1/3

3 x exp(x ) - 15 x exp(x ) + 60 x exp(x ) - 180 x exp(x )

1/3 1/3 1/3

+ 360 x exp(x ) - 360 exp(x )

zad. 6

Obliczyć wartość całki oznaczonej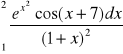

>> clear

>> v=quadl('exp(x.^2).*cos(x+7)./(1+x).^2',1,2)

v =

-1.4715

zad. 7

Znaleźć:
jeżeli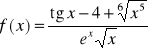
, podać wartość pochodnej w punkcie x=0.75

clear

syms x

poch=diff((tan(x)-4+x^(5/6))/(exp(x)*sqrt(x)),x,3)

poch =

(2*(1+tan(x)^2)^2+4*tan(x)^2*(1+tan(x)^2)+35/216/x^(13/6))/exp(x)/x^(1/2)-3*(2*tan(x)*(1+tan(x)^2)-5/36/x^(7/6))/exp(x)/x^(1/2)-3/2*(2*tan(x)*(1+tan(x)^2)-5/36/x^(7/6))/exp(x)/x^(3/2)+3*(1+tan(x)^2+5/6/x^(1/6))/exp(x)/x^(1/2)+3*(1+tan(x)^2+5/6/x^(1/6))/exp(x)/x^(3/2)+9/4*(1+tan(x)^2+5/6/x^(1/6))/exp(x)/x^(5/2)-(tan(x)-4+x^(5/6))/exp(x)/x^(1/2)-3/2*(tan(x)-4+x^(5/6))/exp(x)/x^(3/2)-9/4*(tan(x)-4+x^(5/6))/exp(x)/x^(5/2)-15/8*(tan(x)-4+x^(5/6))/exp(x)/x^(7/2)

2 2 2 2 35 1

2 (1 + tan(x) ) + 4 tan(x) (1 + tan(x) ) + --- -----

216 13/6

x

------------------------------------------------------

1/2

exp(x) x

2 1

2 tan(x) (1 + tan(x) ) - 5/36 ----

7/6

x

- 3 ----------------------------------

1/2

exp(x) x

2 1 2 1

2 tan(x) (1 + tan(x) ) - 5/36 ---- 1 + tan(x) + 5/6 ----

7/6 1/6

x x

- 3/2 ---------------------------------- + 3 ----------------------

3/2 1/2

exp(x) x exp(x) x

2 1 2 1

1 + tan(x) + 5/6 ---- 1 + tan(x) + 5/6 ----

1/6 1/6

x x

+ 3 ---------------------- + 9/4 ----------------------

3/2 5/2

exp(x) x exp(x) x

5/6 5/6 5/6

tan(x) - 4 + x tan(x) - 4 + x tan(x) - 4 + x

- ----------------- - 3/2 ----------------- - 9/4 -----------------

1/2 3/2 5/2

exp(x) x exp(x) x exp(x) x

5/6

tan(x) - 4 + x

- 15/8 -----------------

7/2

exp(x) x

>>

wartość pochodnej dla x=0.75

val=subs(poch,x,.75)

val =

29.2409

Obliczyć wartość drugiej pochodnej funkcji
w punkcie x=1.25.

Stosując wzór na zamianę podstawy logarytmów mamy:

syms x

v=diff(log(sin(x))/log(x),x,2)

v =

-1/log(x)-cos(x)^2/sin(x)^2/log(x)-2*cos(x)/sin(x)/log(x)^2/x+2*log(sin(x))/log(x)^3/x^2+log(sin(x))/log(x)^2/x^2

pretty(v)

2

1 cos(x) cos(x) log(sin(x)) log(sin(x))

- ------ - -------------- - 2 ---------------- + 2 ----------- + -----------

log(x) 2 2 3 2 2 2

sin(x) log(x) sin(x) log(x) x log(x) x log(x) x

subs(v,x,.5)

ans =

2.5768

zad. 8

Na podstawie podanych pomiarów zmiennych losowych x i y wyznaczyć współczynnik korelacji liniowej r oraz współczynniki a i b równania regresji :

1. liniowej y=ax+b

2. wykładniczej y=ax^b

3. potęgowej y=ae^bx

d) potęgowej y=ab^x

Proszę wskazać funkcję najlepiej aproksymującą i uzasadnić wybór.

x y

1.2 1.05

2 1.24

3.4 1.48

4.7 1.65

5.1 1.7

6.2 1.81

6.4 1.83

7.8 1.96

8.9 2.04

11 2.19

12.5 2.29

>> clear

>> x=[1.2 2 3.4 4.7 5.1 6.2 6.4 7.8 8.9 11 12.5];

>> y=[1.05 1.24 1.48 1.65 1.7 1.81 1.83 1.96 2.04 2.19 2.29];

liniowa y=ax+b

corr2(x,y)

ans =

0.9757

a=polyfit(x,y,1)

a =

1. 1.0899

yw=a(1)*x+a(2);

plot(x,y,'*',x,yw)

potęgowa y=ax^b

>> x1=log(x);

>> y1=log(y);

>> corr2(x1,y1)

ans =

1.0000

>> a=polyfit(x1,y1,1)

a =

0.3331 -0.0139

>> w=exp(a(2))

w =

0.9862

>> yw=w*x.^a(1);

>> plot(x,y,'*',x,yw);

>>

wykładnicza y=ae^bx

>> corr2(x,y1)

ans =

0.9433

>> z=polyfit(x,y1,1)

z =

0.0632 0.1374

>> a=exp(z(2))

a =

1.1473

>> yw=a.*exp(z(1).*x);

>> plot(x,y,'*',x,yw);

>>

potęgowa y=ab^x

corr2(x,y1)

ans =

0.9433

>> z=polyfit(x,y1,1)

z =

0.0632 0.1374

>> a=exp(z(2))

a =

1.1473

>> b=exp(z(1))

b =

1.0652

>> yw=a*b.^x;

>> plot(x,y,'*',x,yw);

>>

zad. 9

Wyznaczyć punkty przecięcia się krzywych:

>> [x y]=solve('(x-3.1)^2+(y-1.2)^2=2.56^2','(x-5.4)^2+(y-2.3)^2=1.21^2','x','y')

x =

[ 5.6586855985700393201512903663581]

[ 4.6422144014299606798487096336419]

y =

[ 1.1179755666262814215018474157967]

[ 3.2433244333737185784981525842033]

>>

>> ezplot('(x-3.1)^2+(y-1.2)^2=2.56^2',[-3 7]);axis equal;hold on;

>> ezplot('(x-5.4)^2+(y-2.3)^2=1.21^2',[-3 7]);axis equal;

zad.10

Znaleźć maksimum wyrażenia

przy ograniczeniach:

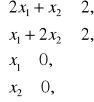
f =[1 3]

a =[2 1; -1 -2]

b =[2 -2]'

Narysujmy obszar wyznaczony przez ograniczenia:

ezplot('2*x1+x2-2',[0 2]);hold on; axis equal;

ezplot('x1+2*x2-2',[0 2]);axis equal

[x fval]=linprog(f,a,b)

Optimization terminated successfully.

x =

0.6667

0.6667

fval =

2.6667

Obliczyć długość krzywej płaskiej:

syms x

l=subs(int(sqrt(diff(log(x),x)^2+1),x,3^(1/2),8^(1/2)))

l =

1.2027

Znaleźć długość łuku krzywej danej równaniem parametrycznym:

ezplot('(t^2-2)*sin(t)+2*t*cos(t)','(2-t^2)*cos(t)+2*t*sin(t)',[0 pi])

syms t

l=int(sqrt(diff((t^2-2)*sin(t)+2*t*cos(t),t)^2+diff((2-t^2)*cos(t)+2*t*sin(t),t)^2),t,0,pi)

l =

1/3*pi^3

Obliczyć długość krzywej płaskiej

clear

syms x

l=int(sqrt(diff((x-3*a)*sqrt(x/a)/3,x)^2+1),x,0,x0)

l =1/6*((x0^2+a^2+2*x0*a)/x0/a)^(1/2)/(a+x0)*x0*(x0+3*a)*4^(1/2)

simple(l)

ans =1/3*x0^(1/2)*(x0+3*a)/a^(1/2)

pretty(ans)

1/2

x0 (x0 + 3 a)

1/3 ----------------

1/2

a

Odp.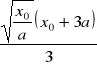
Stwierdzono, że pewna sprężyna nie podlega prawu Hooke'a. Jeżeli jest ona rozciągnięta na odległość x (w metrach), to siła (w Niutonach), którą wywiera w kierunku przeciwnym do rozciągnięcia wyraża się wzorem:

a)

clear

syms x

P=subs(int(52.8*exp((x-0.3)^2)+38.4*x^2,x,.5,1))

P = 44.49594820775996

b)

Obliczyć całkowita pracę potrzebną do rozciągnięcia sprężyny od położenia
m do
m.

Obliczyć pracę jaką trzeba wykonać, aby wyczerpać wodę napełniającą zbiornik w kształcie walca o wysokości h=5 m i promieniu podstawy r=3 m.

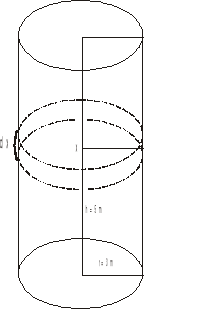
>> syms x

>> v=subs(pi*9*1000*int(5-x,x,0,5))

v = 3.5343e+005 [kGm]

Naczynie ma kształt paraboloidy obrotowej o promieniu podstawy R=2 m i głębokości H=4 m. Ciężar płynu napełniającego naczynie wynosi 0.8 G/cm³ . Znaleźć pracę jaką trzeba wykonać, aby wyczerpać płyn z naczynia.

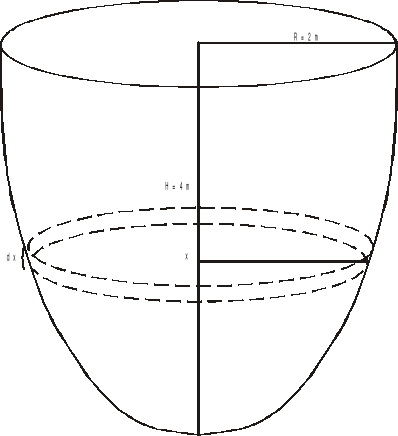
syms x

v=subs(pi*800*int((4-x)*x,x,0,4))

v = 2.6808e+004 [kGm]

Zbiornik ma kształt stożka ściętego o długościach promieni podstaw : dolnej r, górnej R i wysokości h. Obliczyć pracę potrzebną na wypompowanie cieczy z pełnego zbiornika. Ciężar cieczy wynosi γ.

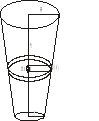
Rozwiązanie:

równanie położenia punktu p w zależności od położenia punktu x na wysokości zbiornika wyraża się wzorem:

objętość dv odpowiadająca przyrostowi dx dla położenia x wynosi:

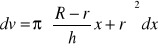
praca potrzebna na wylanie objętości dv ze zbiornika polegająca na podniesieniu objętości dv o ciężarze γ z wysokości x do wysokości h wyraża się wzorem:

By wylać całą zawartą w zbiorniku ciecz, trzeba wykonać pracę

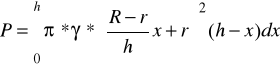
Obliczmy powyższą całkę za pomocą Matlaba

syms x r R h

P=int(((R-r)/h*x+r)^2*(h-x),x,0,h)

P =

-1/4*(R-r)^2*h^2+1/3*(-2*r*(R-r)/h+(R-r)^2/h)*h^3+1/2*(-r^2+2*r*(R-r))*h^2+r^2*h^2

uprośćmy otrzymane wyrażenie

P=simple(P)

P =

1/12*h^2*(R^2+2*R*r+3*r^2)

mnożąc otrzymany wynik przez γ i π otrzymamy

Dla jakich wartości parametru a układ równań (jednorodny) jest nieoznaczony?

(wskazówka: wyznacznik macierzy współczynników jest równy zero)

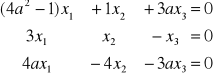
clear

syms a

A=[4*a^2-1 1 3*a;3 1 -1;4*a -4 -3*a]

A =

[ 4*a^2-1, 1, 3*a]

[ 3, 1, -1]

[ 4*a, -4, -3*a]

subs(solve(det(A),a))

ans =

0.12609731741906

-1.22971532537620 + 1.06360761529162i

-1.22971532537620 - 1.06360761529162i

Zadania Matlab

1

---