Sekcja: I środa 16⁰⁰

Grupa: 5

Kierunek: MiBM

Wydział: Mechaniczny-Technologiczny

rok ak. 2001/02

sem. letni

Katedra Wytrzymałości Materiałów

i Metod Komputerowych Mechaniki

LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW

Temat: STATYCZNA PRÓBA SKRĘCANIA METALI

WYZNACZANIE MODUŁU SPRĘŻYSTOŚCI POPRZECZNEJ G

1. Cel próby

Przeprowadzenie statycznej próby skręcania ma na celu:

- pokazanie zachowania się materiału podczas próby;

- wyznaczenie pewnych wielkości charakteryzujących własności materiału (w naszym przypadku w

zakresie odkształceń sprężystych):

- sprawdzenie liniowej zależności kąta skręcenia Φ od momentu skręcającego M_S

- wyznaczenie modułu sprężystości poprzecznej G;

• statystyczne opracowanie wyników.

2. Wstęp

Próbę skręcania przeprowadza się zwykle na prętach o stałym przekroju kołowym, dla których proste jest określenie stanu naprężenia. Próbki o innym niż kołowy przekroju stosowane są w szczególnych wypadkach. Wymiary próbek zwykle wynoszą : d - 10- 30 mm L_o = (5 :-: 20)d, lecz najczęściej L_o=10d.

W przypadku prętów cienkich i drutów można je mocować bezpośrednio w odpowiednich uchwytach. Typowe próbki maja, głowy o przekroju kołowym, kwadratowym, n-kątnym i innych, mogą również posiadać nacięcia. Jednakże bez wzglądu na kształt muszą one spełniać wymóg osiowego ustawienia próbki i uniemożliwić obrót głowy wewnątrz uchwytów. Najczęściej w związku z tym stosuje się próbki z głowami o przekroju kwadratowym.

Jeżeli pręt jest obciążony w płaszczyźnie prostopadłej do jego osi parą sił o momencie K , to siły wewnętrzne zredukują się do momentu M_s, którego kierunek jest zgodny z osią pręta. Moment M_s nazywamy momentem skręcającym.

Odkształcenie (γ) Kąt skręcenia (ϕ) i rozkład naprężeń (τ_max) w pręcie skręcanym

Moment ten powoduje w poszczególnych przekrojach poprzecznych próbki płaski stan naprężenia i odpowiadający mu stan odkształcenia, który dla prętów o przekrojach kołowych w zakresie odkształceń sprężystych określany jest wzorami :

_max =(Ms / Wo )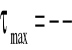

gdzie:

τ_max- największe naprężenia styczne

W_o - wskaźnik wytrzymałości na skręcanie

I_o - biegunowy moment bezwładności przekroju próbki

r - promień przekroju poprzecznego próbki

d_o - początkowa wartość próbki

gdzie:

ϕ - kąt skręcenia

l_o - długość pomiarowa próbki

GI_o - sztywność na skręcanie

G - moduł sprężystości poprzecznej

gdzie:

γ - kąt odkształcenia postaciowego (posunięcie)

3. Stanowisko próby skręcania

Skręcarka firmy Amsler.

Wartości momentów M_prs, M_sps, M_es i M_ms zaznaczone na wykresie mogą posłużyć do wyznaczenia wartości granicznych naprężeń tj. odpowiednio: granicy proporcjonalności, sprężystości, plastyczności oraz wytrzymałości przy skręcaniu.

Wykres skręcania materiału sprężysto - plastycznego

Zaznaczyć tu należy, że próba skręcania lepiej obrazuje własności plastyczne materiału niż próba rozciągania. Wynika to z niezmienności wymiarów przekroju i długości próbki podczas skręcania aż do jej zniszczenia, co pozwala na określenie naprężeń w prze­kroju poprzecznym próbki nawet przy znacznych odkształceniach. W próbie rozciągania było to niemożliwe ze względu na tworzenie się tzw. szyjki.

Ujemną stroną próby skręcania jest nierównomierność rozkładu naprężeń w przekroju poprzecznym próbki, co znacznie komplikuje ujecie zjawiska powyżej granicy sprężystości w formę matematyczną - by uniknąć tego zjawiska stosuje się pręty cienkościenne.

4. Moduł sprężystości poprzecznej G wyznaczamy z równania :

W celu dokładniejszego określenia wartości G zastosujemy metodę statystyczną - metodę najmniejszych kwadratów, która jest jedną z częściej stosowanych metod do analizy wyników doświadczalnych. Jej ideą jest wyznaczanie takiej funkcji y = ƒ(x), która przy założeniu minimum błędu aproksymacji określa zależność pomiędzy otrzymanymi wynikami badań.

W naszym wypadku poszukujemy funkcję :

y = ax + b

gdzie:

y = Ms

x = ϕ

współczynniki “a” i “b” dobieramy tak aby suma kwadratów różnic pomiędzy wartościami doświadczalnymi y, a wartością oczekiwaną ax+b : należy dobrać „a” i „b” minimalizujące sumę :

wprowadzając oznaczenia :

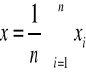
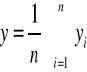
otrzymujemy rozwiązany układ równań w postaci :

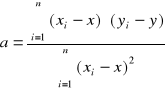
b = y - ax

Dla oceny dokładności pomiarów wyznaczamy wartość odchylenia standardowego:

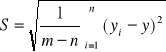
gdzie:

m - ilość pomiarów

n - ilość parametrów (n=2)

5. Obliczenia i wnioski :

Lp.	Ms [kGm]	Ms [Nm]	1 [^o]	2 [^o]	 [^o]	 [rad]	Gi [ x 10^4MPa]
1	3	30	3	1,5	1,5	0,026179939	9,519694903
2	6	60	7	3	4	0,06981317	7,139771177
3	9	90	11,5	4,5	7	0,122173048	6,119803866
4	12	120	16,5	6,5	10	0,174532925	5,711816942
5	15	150	21	8	13	0,226892803	5,492131675
6	18	180	26,5	9,5	17	0,296705973	5,039838478
7	21	210	33	11,5	21,5	0,375245789	4,649153325
8	24	240	40	13	27	0,471238898	4,230975513
9	27	270	48	15	33	0,575958653	3,894420642
10	30	300	58,5	17	41,5	0,72431164	3,44085358
						Gśr [x 10^4MPa]	5,52384601
Długość pręta l= [m].		l=	0,705	m
Średnica pręta d= [mm]:
1	17,12	[mm]
2	17,2	[mm]
3	17,18	[mm]	d=	17,147 mm	=	0,017146667 m
4	17	[mm]
5	17,22	[mm]
6	17,16	[mm]
Dokładność suwmiarki 0,02.

REGRESJA LINIOWA OBLICZENIA.
Statystyki regresji
Wielokrotność R	0,981575718
R kwadrat	0,963490891
Dopasowany R kwadrat	0,958927252
Błąd standardowy	18,40788329
Obserwacje	10

ANALIZA WARIANCJI
	df	S	MS	F	Istotność F
Regresja	1	71539,19866	71539,199	211,1234	4,93067E-07
Resztkowy	8	2710,801337	338,85017
Razem	9	74250

		Współczynniki	Błąd standardowy		t Stat	Wartość -p	Dolne 95%	Górne 95%	Dolne 95,0%	Górne 95,0%
Przecięcie		b=45,68301862	10,06565169		4,538505805	0,001902933	22,4715692	68,894468	22,471569	68,8944681
Zmienna X 1		a=389,5361514	26,80893648		14,53008596	4,93067E-07	327,714593	451,35771	327,71459	451,35771
y=389,53*x+45,68

Obliczenie modułu sprężystości metodą najmniejszych kwadratów szukając współczynnika kierunkowego c₁ prostej aproksymującej.

f(x)=co+c1x

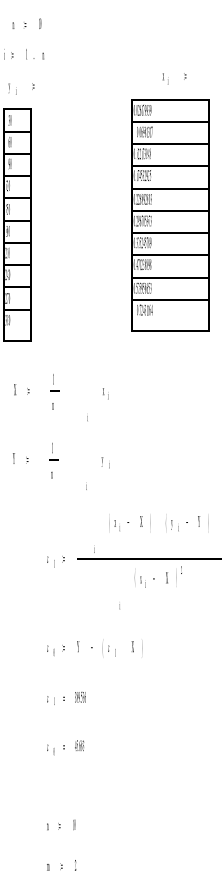
y=389,53*x+45,68

Dla oceny dokładności pomiarów wyznaczamy wartość odchylenia standardowego:

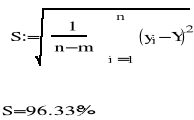
Wyznaczam teraz moduł sprężystości poprzecznej metodą statyczna G_stat:

l_o=0,705 [m]=7050[mm]

d₀=0,17147[m]=17,147 [mm]

G_stat= 5,2361*10⁴ [MPa]

Wnioski:

Moduł Kirchhoffa (sprężystości poprzecznej) G=5,52384601*10⁴ [MPa]

Otrzymane wyniki świadczą o tym , że uzyskaliśmy zamierzony cel.

Statystyka regresji dowodzi , że błąd jest nie wielki różnice R kwadrat wynoszą zaledwie 0,01.

3

---