ROZDZIAŁ 10.
STATYSTYKA MATEMATYCZNA W PROGRAMIE R
10.1. Informacje o programie R
R jest programem przeznaczonym do zaawansowanych analiz statystycznych. Jest objęty licencją GNU GPL, co oznacza, że jest darmowy - zarówno w zastosowaniach edukacyjnych, jak i komercyjnych. Najnowszą wersję programu można ściągnąć ze strony www.r-project.org. Instalacja programu jest bardzo prosta, a sama platforma jest wyposażona w bogatą dokumentację w postaci plików PDF i ma rozbudowaną pomoc. Jest on również świetnym narzędziem do tworzenia różnego rodzaju wykresów charakteryzujących się wysoką jakością. Dzięki istnieniu różnego rodzaju pakietów (ponad 1500) jego możliwości są bardzo duże i w znacznym stopniu poszerzają jego podstawową funkcjonalność. Warto przy tym wspomnieć, że już podstawowa wersja R, bez instalowania dodatkowych pakietów, w większości zastosowań jest w zupełności wystarczająca.
Korzystanie z R sprowadza się do wpisywania ciągu komend, które mają zostać wykonane przez program. Wpisuje się je po tzw. znaku zachęty >.
Po uruchomieniu programu R pojawi się okno powitalne z m.in. informacją, że R jest wolnym oprogramowaniem.
Samo okno programu dla osób korzystających z Excela bądź innych bardziej zaawansowanych pakietów statystycznych może się wydawać stosunkowo ubogie. Jest to jednak złudne wrażenie, gdyż pod wieloma względami R przewyższa komercyjne pakiety, a dzięki temu, że jest nieustannie rozwijany na całym świecie, umożliwia przeprowadzenie zaawansowanych analiz statystycznych.
W kolejnych podrozdziałach omówione zostaną wybrane funkcje umożliwiające znalezienie przedziałów ufności, testowanie hipotez statystycznych, rysowanie wykresów funkcji gęstości itd. W przypadku niektórych omawianych w podręczniku metod, które nie zostały oprogramowane w R, istnieje konieczność samodzielnego wpisywania kodu. Jak jednak pokażemy na przykładach, napisanie samemu kodu nie jest zagadnieniem trudnym, a w istotny sposób skraca czas prowadzenia - często zaawansowanych analiz statystycznych.
10.2. Podstawowe funkcje statystyczne
Jedną z podstawowych struktur danych w programie R jest wektor, który należy rozumieć jako ciąg obiektów tego samego typu (liczb, wartości logicznych, różnego rodzaju znaków). Na wektorach można wykonywać różnego rodzaju operacje (na przykład dodawanie, mnożenie), w wyniku których uzyskujemy również wektor. W szczególnym przypadku możemy jako wynik operacji na wektorach uzyskać liczbę, która jest również wektorem o długości równej 1. Do łączenia obiektów w wektor służy funkcja c().
Poniżej zaprezentowane zostaną najważniejsze funkcje, które wykorzystywane będą
w kolejnych podrozdziałach. Pomoc na temat funkcji można uzyskać wpisując za znakiem zachęty nazwę funkcji poprzedzoną znakiem zapytania. Przykładowo, chcąc uzyskać pomoc na temat średniej wystarczy wydać następującą komendę:
> ?mean #pomoc dla funkcji średnia
W R istnieje możliwość dodawania komentarza, który w przypadku rozbudowanych programów składających się z dużej liczby linijek kodu ułatwia jego późniejszą analizę. Komentarz wstawia się za znakiem #, co jest sygnałem dla R, że fragment kodu po tym znaku należy zignorować przy wykonywaniu ciągu poleceń.
Obecnie pokażemy w jaki sposób wykorzystywać popularne w R funkcje statystyczne do prostych analiz.
Przykład 10.1
Miesięczny zysk (w tys. zł) 10 przedsiębiorstw pewnej branży przedstawiał się następująco: 10, 12, 13, 11, 11, 16, 15, 10, 9, 13. Na przykładzie tej zmiennej oblicz podstawowe statystyki opisowe korzystając z funkcji wbudowanych w R.
Rozwiązanie:
> zysk=c(10,12,13,11,11,16,15,10,9,13) #tworzymy wektor zawierający zysk wszystkich przedsiębiorstw i zapisujemy go do zmiennej zysk
> max(zysk) #zysk maksymalny
[1] 16
> min(zysk) #zysk minimalny
[1] 9
> mean(zysk) #średni zysk
[1] 12
> sum(zysk) #łączny zysk
[1] 120
> sd(zysk) #odchylenie standardowe zysku
[1] 2.260777
> var(zysk) #wariancja zysku
[1] 5.111111
> median(zysk) #mediana zysku
[1] 11.5
> quantile(zysk, 0.25) # kwartyl pierwszy zysku
25%
10.25
> quantile(zysk, 0.75) # kwartyl trzeci zysku
75%
13
> IQR(zysk) #rozstęp międzykwartylowy
[1] 2.75
> length(zysk) #liczebność próby
[1] 10
> range(zysk) # przedział zmienności próby (wartość minimalna
i maksymalna)
[1] 9 16
> summary(zysk) # proste podsumowanie wektora z danymi
Min. 1st Qu. Median Mean 3rd Qu. Max.
9.00 10.25 11.50 12.00 13.00 16.00
Pewnego wyjaśnienia wymaga funkcja sd(). Służy ona do wyznaczania odchylenia standardowego z próby ze wzoru:
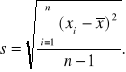
(10.1)
Chcąc wyznaczyć ocenę odchylenia standardowego z próby w oparciu o wzór:
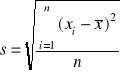
(10.2)
należy skorzystać z równości:
![]()
. (10.3)
> sqrt(9/10)*sd(zysk) # wyznaczamy odchylenie standardowe z próby ze wzory (10.2). Funkcja sqrt() zwraca pierwiastek z podanej liczby.
[1] 2.144761
10.3. Wybrane rozkłady zmiennych losowych
Program R posiada rozbudowane możliwości w zakresie obliczania wartości funkcji gęstości i dystrybuanty w punkcie oraz kwantyli dowolnego rzędu wielu znanych
z rachunku prawdopodobieństwa zmiennych losowych. Można go również wykorzystywać jako generator liczb losowych z dowolnego rozkładu. Wśród wielu rozkładów zmiennych losowych dostępne są również: rozkład normalny (norm), t-Studenta (t), ![]()
(chisq) oraz F Fishera-Snedecora (f). Kiedy poprzedzimy nazwę każdego z tych rozkładów literą d, p, q bądź r uzyskamy odpowiednio komendy służące do wyznaczania wartości funkcji gęstości w punkcie, wartości dystrybuanty w punkcie, kwantyla oraz generator liczb losowych.
Przykład 10.2
Załóżmy, że miesięczny zysk przedsiębiorstw z pewnej branży (w tys. zł) ma rozkład normalny ![]()
. Oblicz:
a) ![]()
,
b) ![]()
,
c) ![]()
,
d) wszystkie kwartyle.
Rozwiązanie:
Celem obliczenia odpowiednich prawdopodobieństw wykorzystamy funkcję programu R pnorm(x,m,σ). W przypadku kwantyli skorzystamy natomiast z funkcji statystycznej qnorm(![]()
,m,σ), gdzie ![]()
oznacza rząd kwantyla.
a)
> pnorm(75,70,10)
[1] 0.6914625
b)
> 1-pnorm(90,70,10)
[1] 0.02275013
c)
> pnorm(75,70,10)-pnorm(60,70,10)
[1] 0.5328072
d)
Q1:
> qnorm(0.25,70,10)
[1] 63.2551
Q2:
> qnorm(0.5,70,10)
[1] 70
Q3:
> qnorm(0.75,70,10)
[1] 76.7449
Przykład 10.3
Korzystając z odpowiedniej funkcji wbudowanej w programie R rozwiązać zadanie
z przykładu 2.1.
Rozwiązanie:
> 1-pnorm(120,100,10)
[1] 0.02275013
Przykład 10.4
Korzystając z odpowiednich funkcji wbudowanych w programie R znaleźć wartości funkcji gęstości następujących rozkładów w punkcie x=10.
a ) N(10,1),
b) t(5),
c) ![]()
,
d) F(20,5).
Rozwiązanie:
a)
> dnorm(10,10,1)
[1] 0.3989423
b)
> dt(10,5)
[1] 4.098982e-05
c)
> dchisq(10,1)
[1] 0.0008500367
d)
> df(10,20,5)
[1] 0.002058857
Przykład 10.5
Korzystając z odpowiedniej funkcji wbudowanej w programie R znaleźć wartość krytyczną ![]()
z przykładu 4.1.
Rozwiązanie:
> qt(1-0.05/2,9)
[1] 2.262157
Wartość 0,975 (1-0,05/2) wzięta zamiast 0,05, którą przyjęto do odczytania wartości krytycznej z tablic w przykładzie 4.1 wynika z nieco innego sposobu w jaki R wyznacza wartość kwantyla w rozkładzie t-Studenta. Ponieważ rozkład ten stosowany jest z reguły
z uwzględnieniem jego „dwóch ogonów” oznacza to, że krytyczne 5% jest podzielone na dwa końce.
Przykład 10.6
Korzystając z odpowiedniej funkcji wbudowanej w programie R znaleźć wartość krytyczną ![]()
z przykładu 4.2.
Rozwiązanie:
> qnorm(1-0.05/2,0,1)
[1] 1.959964
Przykład 10.7
Korzystając z odpowiedniej funkcji wbudowanej w programie R wygenerować 10 obserwacji z rozkładu N(5,1).
Rozwiązanie:
> rnorm(10,5,1)
[1] 4.318904 5.350016 6.578122 5.138987 4.392612 4.252655 5.488534 3.948452 5.167303 2.925853
Oczywiście ze względu na to, że jest to generator liczb losowych za każdym razem wywołując funkcję rnorm(10,5,1) uzyskamy inne wyniki.
10.4. Wykresy funkcji
Program R umożliwia rysowanie wykresów dowolnych funkcji matematycznych.
W tym podrozdziale pokażemy w jaki sposób wykorzystać go do stworzenia wykresów funkcji gęstości oraz dystrybuanty wybranych zmiennych losowych omawianych
w podręczniku. Rysowane wykresy mogą być dodawane do istniejących lub stanowić oddzielną część. Podstawową komendą w programie R służącą do tworzenia wykresów jest curve(). Jej składnia jest następująca:
curve(f(x), opcje),
gdzie f(x) oznacza nazwę funkcji (na przykład sin(x), dnorm(x)) bądź określoną jej postać, a opcje odnoszą się do bardzo bogatego zestawu parametrów, którymi można sterować podczas tworzenia wykresu.
Do najważniejszych z nich należą:
add - opcja służąca do rysowania wielu wykresów w jednym układzie współrzędnych;
ask - opcja ta służy do rysowania wykresów funkcji etapami. Przed rozpoczęciem ryzowania użytkownik chcąc przejść do następnej części wykresu musi nacisnąć dowolny klawisz. Domyślną wartością tej opcji jest FALSE. Chcąc zatem ją wykorzystać jako argument funkcji curve() należy jej wartość zmienić na TRUE;
bg - opcja ta służy do ustalenia tła koloru;
bty - opcja służąca do modyfikowania ramki wykresu. Pełną ramkę program rysuje domyślnie, jednak ustawiając w opcjach bty=”n” uzyskuje się wykres bez ramki, bty=”l” służy do kodowania lewej i dolnej części ramki, bty=”7” do jej górnej i prawej części, bty=”c” nie rysuje prawej ramki, a bty=”u” górnej ramki;
cex - opcja służąca do zmiany wielkości czcionki tekstu lub legendy (domyślna wielkość to 1);
col - opcja wykorzystywana w zależności od przeznaczenia do ustalenia koloru linii, słupków itd. wykresu (domyślnie col=”black”);
col.axis - opcja służąca do zmieniania koloru wartości wyświetlanych na osi rzędnych i odciętych (domyślnie col.axis=”black”);
col.lab - opcja służąca do zmiany koloru legendy osi odciętych i rzędnych (domyślnie col.lab=”black”);
col.main - opcja ta służy do zmiany koloru głównego tytułu wykresu (domyślnie col.main=”black”);
col.sub - opcja ta służy do zmiany koloru podtytułów (domyślnie col.sub=”black”;
fg - opcja służąca do zmiany koloru powierzchni wykresów - osi oraz różnego rodzaju pudełek otaczających wykres (domyślnie fg=”black”);
font - opcja służąca do zmiany czcionki. 1 - tekst normalny, 2 - tekst pogrubiony, 3 - kursywa, 4 - pogrubiona kursywa;
lty - opcja służąca do zmiany wyglądu linii wykresu. 1 - linia ciągła, 2 - linia kreskowana, 3 - linia kropkowana, 4 - linia typu kropka-kreska, 5 - linia w postaci długiej kreski, 6 - linia w postaci podwójnej kreski (domyślnie lty=1);
lwd - opcja służąca do zmiany grubości linii wykresu (domyślnie lwd=1);
main - opcja ta służy do nadawania wykresowi tytułu;
pch - opcja służąca do zmiany symbolu oznaczającego punkt na wykresie. Na przykład pch=”x” oznacza, że punkty na wykresie oznaczone zostaną symbolem x. Domyślnie punkty te oznaczane są na wykresie symbolem ○;
xlab, ylab - opcje służące do umieszczania napisów na osiach x i y;
xlim, ylim - opcje te służą do określania przedziałów zmienności dla x i y.
Ponadto używając komendy text(x,y,tekst), gdzie x i y oznaczają współrzędne tekstu, można umieszczać na wykresach różnego rodzaju napisy.
Przykład 10.8
Sporządź wykres funkcji gęstości zmiennej losowej ![]()
.
Rozwiązanie:
Aby sporządzić wykres funkcji gęstości zmiennej losowej o rozkładzie normalnym należy wykorzystać funkcję dnorm(x,m,σ). Wyznacza ona wartość funkcji gęstości zmiennej losowej o rozkładzie normalnym z wartością oczekiwaną m oraz odchyleniem standardowym σ w punkcie x. Wpisujemy następujące polecenie:
> curve(dnorm(x,10,3),xlim=c(1,19),ylim=c(0,0.15),lwd=2,xlab="Źródło: Opracowanie własne", ylab="f(x)",main="Funkcja gęstości rozkładu normalnego N(10,3)",bty="o")
W rezultacie otrzymamy następujący wykres:
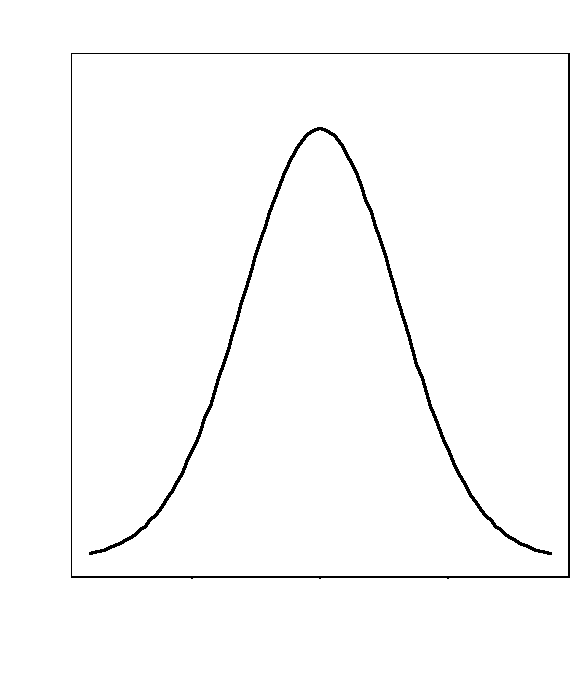
W przykładzie tym jako zakres zmienności dla x przyjęto przedział (1,19). Jest to konsekwencją reguły 3σ, która mówi, że jeżeli zmienna losowa ma rozkład normalny
z wartością oczekiwaną m i odchyleniem standardowym σ, to w przedziale (m-3σ,m+3σ) znajduje się około 99,7% wszystkich jednostek ze względu na badaną cechę. Rysując więc wykres tej funkcji i chcąc uzyskać charakterystyczny dla tej krzywej kształt kapelusza wystarczy ograniczyć się do tego przedziału.
Przykład 10.9
Na jednym rysunku sporządzić wykresy funkcji gęstości zmiennych losowych
o rozkładzie normalnym: N(0,1), N(0,2) i N(0,3).
Rozwiązanie:
W pierwszym kroku wydajemy komendę (w jednej linijce):
> curve(dnorm(x,0,1),xlim=c(-9,9),ylim=c(0,0.4),lty=1,xlab="Źródło:
Opracowanie własne",ylab='f(x)',main="Funkcje gęstości rozkładu normalnego"); curve(dnorm(x,0,2),lty=2,add=T);
curve(dnorm(x,0,3),add=T,lty=3)
W efekcie wywołania tej komendy na jednym rysunku program R umieści wszystkie trzy funkcje gęstości zmiennych losowych o rozkładzie normalnym dla różnych wartości parametru σ. Następnie chcąc dodać legendę w kolejnej linijce wpisujemy komendę:
> legend(5,0.3,legend=c("N(0,1)","N(0,2)","N(0,3)"),lty=1:3)
Liczby 5 i 0.3 wskazują w układzie współrzędnych miejsce, w którym zostanie umieszczona legenda, wektor legend=c() zawiera poszczególne wpisy legendy,
a lty=1:3 wskazuje, że poszczególnym wpisom legendy należy przypisać oznaczenia
w postaci linii (ciągłej, kreskowanej i kropkowanej) - zgodnie z tym jak zadeklarowano sposób wyświetlania na wykresie poszczególnych funkcji gęstości.
Przykład 10.10
Sporządź wykres funkcji gęstości zmiennej losowej o rozkładzie t-Studenta z 5 stopniami swobody.
Rozwiązanie:
Chcąc narysować funkcję gęstości zmiennej losowej o rozkładzie t-Studenta z k-stopniami swobody należy skorzystać z funkcji dt(x,k).
Wydajemy zatem komendę:
> curve(dt(x,5),xlim=c(-3,3),ylim=c(0,0.4),lty=1,xlab="Źródło: Opracowanie własne",ylab='f(x)',main="Funkcja gęstości rozkładu t-Studenta")
W następnej linii kodu chcąc dodać legendę wydajemy polecenie:
> legend(1.5,0.3,legend=c("t(5)"),lty=1)
W efekcie uzyskujemy wykres poszukiwanej funkcji gęstości oraz legendę.
Przykład 10.11
Sporządź wykres funkcji gęstości zmiennej losowej o rozkładzie ![]()
z 5 stopniami swobody.
Rozwiązanie:
Chcąc narysować funkcję gęstości zmiennej losowej o rozkładzie ![]()
z k-stopniami swobody należy skorzystać z funkcji dchisq(x,k).
Wydajemy zatem komendę:
> curve(dchisq(x,5),xlim=c(0,15),ylim=c(0,0.2),lty=1,xlab="Źródło: Opracowanie własne",ylab='f(x)',main="Funkcja gęstości rozkładu chi-kwadrat")
W następnej linii kodu chcąc dodać legendę wydajemy polecenie:
> legend(10,0.1, legend=c(expression(chi^2~(5))), lty=1)
W rezultacie uzyskujemy wykres funkcji gęstości rozkładu ![]()
z 5-stopniami swobody wraz z legendą.
Przykład 10.12
Sporządź wykres funkcji gęstości zmiennej losowej o rozkładzie F Fishera-Snedecora z 5
i 20 stopniami swobody.
Rozwiązanie:
Chcąc narysować funkcję gęstości zmiennej losowej o rozkładzie F Fishera-Snedecora z k1
i k2 stopniami swobody należy skorzystać z funkcji df(x, k1, k2).
Wydajemy zatem komendę:
> curve(df(x,5,20),xlim=c(0,10),ylim=c(0,0.7),lty=1,xlab="Źródło: Opracowanie własne",ylab='f(x)',main="Funkcja gęstości rozkładu F Fishera-Snedecora")
W następnej linii kodu chcąc dodać legendę wydajemy polecenie:
> legend(6,0.4,legend=c("F(5,20)"),lty=1)
W rezultacie uzyskujemy wykres funkcji gęstości rozkładu F z 5 i 20 stopniami swobody wraz z legendą.
Przykład 10.13
Sporządź wykres dystrybuanty zmiennej losowej o rozkładzie normalnym standaryzowanym.
Rozwiązanie:
Chcąc narysować wykres dystrybuanty zmiennej losowej o rozkładzie normalnym standaryzowanym należy skorzystać z funkcji pnorm(x,m,σ).
Wydajemy zatem komendę:
> curve(pnorm(x,0,1),xlim=c(-3,3),ylim=c(0,1),lty=1,xlab="Źródło: Opracowanie własne",ylab='F(x)',main="Dystrybuanta rozkładu N(0,1)")
W rezultacie uzyskujemy wykres poszukiwanej dystrybuanty.
W analogiczny sposób chcąc znaleźć wykresy dystrybuanty zmiennych losowych
o rozkładzie t-Studenta, ![]()
i F Fishera-Snedecora należy skorzystać odpowiednio
z funkcji pt(x,k), pchisq(x,k) oraz pf(x, k1, k2).
Przykład 10.14
Oblicz kwantyl rzędu 0,95 w rozkładzie normalnym standaryzowanym oraz przedstaw jego interpretację geometryczną na wykresie funkcji gęstości.
Rozwiązanie:
Do wyznaczenia kwantyla ![]()
rzędu α w rozkładzie normalnym z wartością oczekiwaną
m i odchyleniem standardowym σ należy wykorzystać funkcję qnorm(α, m, σ). Wpisujemy więc za znakiem > następujące polecenie qnorm(0.95,0,1), w efekcie czego na ekranie ukaże się następujący wynik:
> qnorm(0.95,0,1)
[1] 1.644854
Stąd ![]()
Geometryczną interpretacją kwantyla rzędu α w rozkładzie normalnym standaryzowanym jest pole powierzchni pod wykresem funkcji gęstości w przedziale od ![]()
do ![]()
. Pole to wynosi α.
Aby przedstawić interpretację geometryczną kwantyla na wykresie funkcji gęstości rozkładu normalnego standaryzowanego użyteczna okaże się funkcja seq, rep, rev oraz poligon.
Funkcja seq pozwala generować składowe wektora od pewnej wartości a do innej wartości b z góry określonym krokiem bądź przy podaniu liczby elementów ciągu za pomocą opcji length krok jest ustalany automatycznie tak, aby wartości były rozłożone równomiernie.
W pierwszej kolejności wydajemy komendę:
> a=seq(-3,qnorm(0.95,0,1),length=50)
W efekcie utworzony zostanie wektor a złożony z 50 wartości równomiernie rozłożonych pomiędzy liczbą -3 a wartością kwantyla tj. 1,64. Aby się o tym przekonać wystarczy
w kolejnej linijce napisać:
> a
aby wyświetlić składowe wektora a. W kolejnym kroku wyznaczamy wartość funkcji gęstości rozkładu normalnego standaryzowanego dla każdej składowej wektora
a i zapisujemy je jako elementy wektora b.
> b=dnorm(a,0,1)
Podobnie możemy wyświetlić na ekranie wszystkie składowe tego wektora wpisują
w kolejnej linijce komendę.
> b
Następnie rysujemy wykres funkcji gęstości rozkładu normalnego standaryzowanego, do którego w następnym kroku dołączymy odpowiednio zaciemniony fragment pola pod tą krzywą. Wpisujemy komendę:
> curve(dnorm(x,0,1),xlim=c(-3,3),main="Interpretacja geometryczna kwantyla rzędu 0.95",ylab="f(x)",xlab="Źródło: Opracowanie własne")
W efekcie wywołania tej komendy otrzymujemy funkcję gęstości rozkładu normalnego standaryzowanego.
Ostatni krok polega na wykorzystaniu funkcji poligon(), która służy do rysowania wielokąta o zadanych współrzędnych x i y.
Wykorzystana w poniższej komendzie funkcja rev() służy do zamiany miejscami elementów wektora w taki sposób, że pierwszy element wyjściowego wektora (na przykład wektora w) staje się ostatnim elementem wektora rev(w), drugi element wektora w staje się przedostatnim elementem wektora rev(w) itd. Funkcja rep() służy z kolei na powtórzenie wektora określoną liczbę razy na przykład rep(c(1,2,3),2) jest równoważne wektorowi c(1,2,3,1,2,3).
Chcąc zaciemnić obszar pod krzywą od ![]()
(aby uzyskać odpowiedni efekt wystarczy przyjąć jako lewy koniec -3) do wartości kwantyla należy wpisać następujące komendę:
> polygon(c(a,rev(a)),c(rep(0,50),rev(b)),col="gray")
> text(0,0.2,"P=0.95")
> text(1.95,0.01,"1.64")
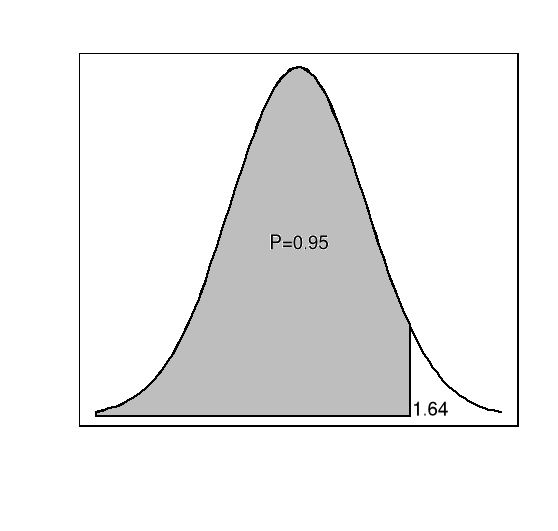
Pakiet R posiada również rozbudowane możliwości rysowania funkcji gęstości zmiennych losowych dwuwymiarowych. Sporządzenie wykresy takiej funkcji wymaga jednak nieco większego wysiłku niż w przypadku jednowymiarowym. Dla przykładu sporządzimy wykres funkcji gęstości zmiennej losowej o rozkładzie normalnym dwuwymiarowym.
Przykład 10.15
Narysuj wykres dowolnej funkcji gęstości zmiennej losowej o rozkładzie normalnym dwuwymiarowym.
Rozwiązanie:
Funkcja gęstości zmiennej losowej o rozkładzie normalnym dwuwymiarowym wyraża się następującym wzorem:
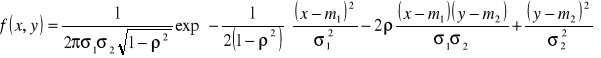
(10.4)
gdzie parametry ![]()
są odpowiednio wartościami oczekiwanymi i odchyleniami standardowymi, zaś ![]()
współczynnikiem korelacji zmiennych losowych X i Y.
Dla przykładu utwórzmy wykres dwuwymiarowej funkcji gęstości o rozkładzie normalnym z parametrami ![]()
, ![]()
, ![]()
, ![]()
oraz ![]()
W pierwszym etapie wpisujemy komendy, w których deklarujemy wartości parametrów.
> m1=0 # wartość oczekiwana zmiennej x
> m2=0 # wartość oczekiwana zmiennej y
> s1=10 # wariancja zmiennej x
> s2=10 # wariancja zmiennej y
> rho=0.5 # współczynnik korelacji pomiędzy zmiennymi x i y
W dalszej kolejności tworzymy dwa wektory x i y, których składowe stanowią wygenerowane wartości z przedziału (-10,10).
> x=seq(-10,10,length=41) # generowanie wartości składowych wektora x
> y=x # wektor y jest tożsamościowo równy wektorowi x
Następnie wprowadzamy pewne pomocnicze zmienne, które ułatwią nam obliczenie wartości funkcji gęstości dwuwymiarowej zmiennej losowej o rozkładzie normalnym
w punktach stanowiących składowe wygenerowanych wektorów x i y, deklarując jednak, że f jest funkcja dwóch zmiennych x i y.
> f=function(x,y)
> {z1=1/(2*pi*sqrt(s1*s2*(1-rho^2)))
> z2=-1/(2*(1-rho^2))
> z3=(x-m1)^2/s1
> z4=(y-m2)^2/s2
> z5=2*rho*((x-m1)*(y-m2))/(sqrt(s1*s2))
> z6=z1*exp(z2*(z3+z4-z5))}
W dalszym etapie wykorzystujemy funkcję outer(x,y,f), która służy do tworzenia tablic wielowymiarowych. W naszym przypadku wektory x i y są argumentami dla funkcji f opisującej gęstość rozkładu normalnego dwuwymiarowego. Funkcja ta wykorzystywana jest jako argument funkcji persp, która służy do rysowania wykresów w przestrzeni ![]()
.
W naszym przypadku outer(x,y,f) przechowuje wartości funkcji gęstości dwuwymiarowego rozkładu normalnego dla wszystkich możliwych par jakie można utworzyć ze składowych wektorów x i y.
> z=outer(x,y,f)
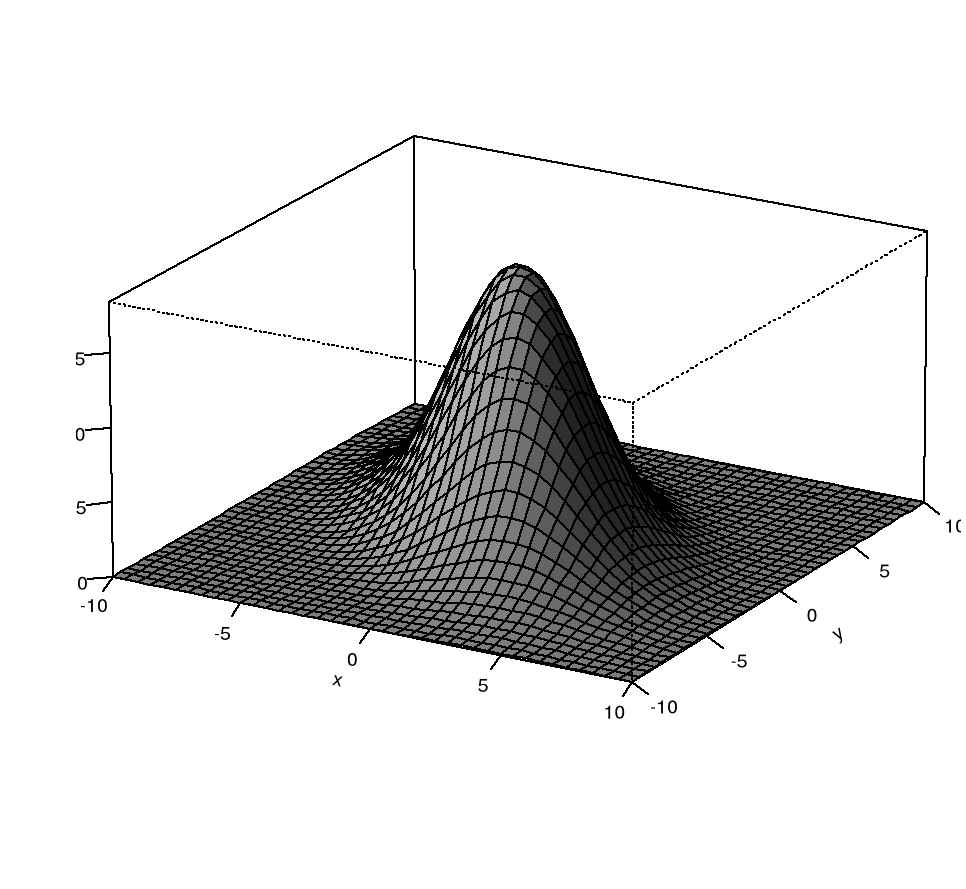
Końcowy etap polega na narysowaniu wykresu funkcji gęstości korzystając z funkcji persp.
Wpisujemy komendę:
> persp(x, y, z, main="Wykres gęstości dwuwymiarowej zmiennej losowej o rozkładzie normalnym", sub=”Źródło: Opracowanie własne”, col="lightgray", theta=30, phi=20,r=50, d=0.1,expand=0.5,ltheta=90, lphi=180, shade=0.75, ticktype="detailed", nticks=5)
W rezultacie uzyskujemy wykres dwuwymiarowej funkcji gęstości rozkładu normalnego.
Opcje funkcji persp: main, sub, col, theta, phi, r, d expand, ltheta, lphi, shade, ticktype oraz nticks służą do nadawania wykresowi tytułu, podtytułu (źródła), koloru oraz umożliwiają zarządzanie położeniem wykresu. Chcąc uzyskać szczegółowe informacje na temat funkcji persp wraz z jej wszystkimi opcjami wystarczy wpisać komendę:
> ?persp
10.5. Estymacja przedziałowa
W programie R istnieje możliwość budowania przedziałów ufności dla wybranych parametrów z wykorzystaniem odpowiednich komend. Dla niektórych parametrów istnieje jednak konieczność konstrukcji przedziałów ufności w oparciu o ogólnie dostępne funkcje operujące na wektorach danych. W podrozdziale tym pokażemy jak samodzielnie oraz wykorzystując funkcje wbudowane w programie R, zbudować przedziały ufności dla dwóch najczęściej spotykanych w praktyce badań statystycznych parametrów: średniej oraz wskaźnika struktury.
10.5.1. Przedział ufności dla średniej
Aby wyznaczyć przedział ufności dla średniej należy skorzystać z funkcji t.test(). Funkcja ta w zasadzie służy do weryfikacji hipotez dla średniej - można jednak ją wykorzystać do zbudowania przedziału ufności dla średniej. Należy jednak zauważyć, że przedział ufności dla średniej funkcja ta wyznacza w oparciu o wzór (4.8 lub 4.9) bez względu na liczebność próby (przy założeniu, że odchylenie standardowe ![]()
w populacji generalnej nie jest znane). Trzymając się jednak konwencji przyjętej w podręczniku pokażemy w jaki sposób wykorzystać tą funkcję w konstrukcji przedziału ufności dla średniej gdy ![]()
oraz jak samemu zbudować taki przedział, gdy ![]()
.
Przykład 10.16
Metodą przedziałową oszacuj średnie przychody ze sprzedaży największych polskich przedsiębiorstw z Listy 2000 publikowanej przez Rzeczpospolitą (31. 10. 2007), jeśli dla 8 losowo wybranych z tej listy przedsiębiorstw uzyskano następujące wyniki (w tys. zł): 297, 276, 228, 315, 193, 208, 211, 227. Przyjmij ![]()
Rozwiązanie:
W pierwszej kolejności zebrane dane zapisujemy do wektora przychod.
> przychod=c(297, 276, 228, 315, 193, 208, 211, 227)
Następnie wpisujemy komendę:
> t.test(przychod)
W rezultacie uzyskujemy następujący wynik:
One Sample t-test
data: przychod
t = 15.2374, df = 7, p-value = 1.263e-06
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
206.4516 282.2984
sample estimates:
mean of x
244.375
Zwróćmy uwagę, że w pierwszej kolejności program zwraca pewne charakterystyki związane z testowaniem hipotezy dla jednej średniej. Zagadnieniu temu poświęcony będzie kolejny podrozdział. W dalszej części podawany jest 95% (domyślnie) przedział ufności dla średniej oraz sama średnia z próby. Wynika stąd, że przedział od 206,45 tys. zł do 282, 3 tys. zł z prawdopodobieństwem 0,95 pokrywa średnie przychody ze sprzedaży wszystkich przedsiębiorstw z Listy 2000.
Chcąc uzyskać szczegółową pomoc na temat tej funkcji wystarczy wpisać w R komendę ?t.test. W rezultacie dostaniemy pomoc, z której można w bardzo łatwy sposób modyfikować pewne domyślne ustawienia. Na przykład, wpisując conf.level=0.99 jako jedną z opcji za nazwą zmiennej można zmienić domyślną wartość współczynnika ufności z 0,95 na 0,99.
Przykład 10.17
Korzystając z danych z przykładu 4.1 skonstruuj przedział ufności dla średnich plonów ziemniaków w indywidualnych gospodarstwach rolnych w województwie wielkopolskim
w roku 2006.
a) Przyjmując tak jak w przykładzie 4.1 współczynnik ufności 0,95.
b) Przyjmując współczynnik ufności 0,99.
a) Przykład a, rozwiążemy na 2 sposoby. W pierwszym wykorzystamy pewne ogólne funkcje statystyczne opisane w podrozdziale 10.1. W drugim przypadku wykorzystamy funkcję t.test().
I sposób (wykorzystamy wzór 4.9)
Uzyskane dane zapisujemy do wektora plony. W tym celu wpisujemy polecenie:
> plony=c(210,195,245,200,180,220,185,205,215,175)
Liczymy średnią z próby ![]()
oraz odchylenie standardowe ![]()
. Zapisujemy je do zmiennych srednia i s. Ponadto liczebność próby zapisujemy do zmiennej n.
> srednia=mean(plony)
> s=sd(plony)
> n=length(plony)
Liczymy wartość krytyczną ![]()
i zapisujemy ją do zmiennej t:
> t=qt(1-0.05/2,9)
Wyznaczamy lewy i prawy koniec przedziału ufności dla średniej i zapisujemy je jako składowe wektora przedzial:
> przedzial=c(srednia-t*s/sqrt(n),srednia+t*s/sqrt(n))
Chcąc wyświetlić przedział wpisujemy komendę przedzial i uzyskujemy następujący komunikat:
> przedzial
[1] 187.9945 218.0055
II sposób:
Wpisujemy polecenie:
> t.test(plony)
W rezultacie uzyskujemy następujący komunikat:
One Sample t-test
data: plony
t = 30.6034, df = 9, p-value = 2.079e-10
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
187.9945 218.0055
sample estimates:
mean of x
203
Przedział liczbowy o końcach 188 i 218 q/ha z prawdopodobieństwem równym 0,95 pokrywa średnie plony ziemniaków w indywidualnych gospodarstwach rolnych w woj. wielkopolskim w roku 2006.
b) Podpunkt ten rozwiążemy tylko korzystając z funkcji t.test() oraz z opcji conf.level.
Wpisujemy w wiersz poleceń następującą komendę:
> t.test(plony,conf.level=0.99)
W rezultacie uzyskujemy następujący efekt:
One Sample t-test
data: plony
t = 30.6034, df = 9, p-value = 2.079e-10
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
181.4430 224.5570
sample estimates:
mean of x
203
Przedział liczbowy o końcach 181,44 i 224,6 q/ha z prawdopodobieństwem równym 0,99 pokrywa średnie plony ziemniaków w indywidualnych gospodarstwach rolnych w woj. wielkopolskim w roku 2006.
W przypadku, gdy znane jest odchylenie standardowe ![]()
bądź liczebność próby spełnia warunek ![]()
, nie ma w R gotowej funkcji na przedział ufności dla średniej. Przedział ufności można jednak w bardzo prosty sposób wyznaczyć, podobnie jak w przykładzie 10. podpunkt (a), korzystając z innych wbudowanych w R funkcji.
Przykład 10.18
Zbuduj 90% przedział ufności dla średnich miesięcznych zarobków brutto pracowników pewnej dużej firmy jeśli w losowej próbie 100 pracowników uzyskano następujące wyniki ![]()
zł i ![]()
zł.
Rozwiązanie:
W rozwiązaniu tego zadania skorzystamy ze wzoru (4.11). Wpisujemy polecenia:
> srednia=2500
> s=400
> z=qnorm(1-0.1/2,0,1)
> n=100
> przedzial=c(srednia-z*s/sqrt(100),srednia+z*s/sqrt(100))
> przedzial
W rezultacie uzyskujemy poszukiwany przedział ufności:
[1] 2434.206 2565.794
Przedział liczbowy o końcach 2434,2 zł i 2565,8 zł z prawdopodobieństwem równym 0,9 pokrywa średnie miesięczne zarobki brutto wszystkich pracowników tego przedsiębiorstwa.
Przykład 10.19
Załóżmy, że wzrost studentów UE w Poznaniu jest zmienną losową o rozkładzie normalnym ![]()
Korzystając z generatora liczb losowych w R wygenerować wzrost 50 studentów z tego rozkładu. Na podstawie próby skonstruować 95% przedział ufności dla średniego wzrostu wszystkich studentów UE. Co można powiedzieć o tak skonstruowanym przedziale ufności?
Rozwiązanie:
W pierwszej kolejności korzystając z funkcji rnorm() wygenerujemy wzrost 50 studentów
i zapiszemy uzyskane wartości do wektora wzrost. Oczywiście za każdym razem wpisując w wiersz poleceń wywołanie tej funkcji dostaniemy inne wyniki. Przyjmiemy przy tym, że wzrost podany będzie z dokładnością do 1 miejsca po przecinku (funkcja format()).
> wzrost=rnorm(50,175,10)
> format(wzrost,digits=4)
W naszym przypadku uzyskano następujące wyniki:
[1] "174.7" "179.7" "189.4" "172.2" "184.0" "193.0" "174.6" "154.4" "188.7" "185.2" "169.5" "161.8" "175.7" "169.3" "153.0" "158.9" "184.0" "174.3" "162.7"
[20] "197.0" "175.4" "185.6" "169.9" "179.9" "167.4" "160.3" "175.8" "175.2" "170.8" "174.2" "177.6" "179.6" "160.9" "174.1" "183.0" "191.1" "167.9" "170.5"
[39] "170.7" "175.7" "187.6" "162.6" "178.3" "173.3" "166.6" "159.2" "185.2" "172.6" "153.9" "172.0"
W dalszej kolejności liczymy średnią i odchylenie standardowe z próby oraz odpowiedni kwantyl i zapisujemy je do zmiennych srednia, s, oraz z odpowiednio.
> srednia=mean(wzrost)
> s=sqrt(49/50)*sd(wzrost)
> z=qnorm(1-0.05/2,0,1)
Następnie korzystając ze wzoru (4.11) wyznaczamy lewy i prawy koniec przedziału ufności dla średniej wzrostu wszystkich studentów UE.
> przedzial=c(srednia-z*s/sqrt(50),srednia+z*s/sqrt(50))
> przedzial
[1] 171.1170 176.8278
Uzyskaliśmy przedział liczbowy od 171,1 cm do 176,8 cm. Zauważmy, że tak skonstruowany przedział pokrywa rzeczywisty średni wzrost (175 cm) wszystkich studentów UE w Poznaniu. Gdybyśmy wiele razy przeprowadzili opisaną tutaj procedurę generowania wzrostu dla 50 studentów, to mogłoby się zdarzyć, że skonstruowany
w oparciu o taką próbę przedział nie pokrywałby rzeczywistego średniego wzrostu studentów. Niemniej jednak w około 95% przypadków otrzymywalibyśmy przedziały pokrywające średni wzrost, a tylko w około 5% przypadków, przedział nie pokrywałby prawdziwej wartości średniej. W ten właśnie sposób należy rozumieć współczynnik ufności - jako prawdopodobieństwo pokrycia przez przedział ufności nieznanego parametru w populacji generalnej.
10.5.2. Przedział ufności dla wskaźnika struktury (frakcji)
Aby wyznaczyć przedział ufności dla wskaźnika struktury należy skorzystać z funkcji prop.test(). Funkcja ta w zasadzie służy do weryfikacji hipotez dla jednej lub dwóch frakcji - można ją jednak wykorzystać do zbudowania przedziału ufności dla wskaźnika struktury.
Przykład 10.20
Zbuduj 99% przedział ufności dla frakcji osób będących zwolennikami obecnego rządu, jeśli w badaniu na losowej próbie 1000 dorosłych Polaków 350 zadeklarowało poparcie dla rządu.
Rozwiązanie:
Wykorzystujemy funkcję prop.test() deklarując ile jednostek w próbie jest wyróżnionych
ze względu na badaną cechę, jaka jest jej liczebność oraz jaki jest poziom przyjętego
w zadaniu współczynnika ufności. W wiersz poleceń wpisujemy następujące polecenie:
> prop.test(350,1000,conf.level=0.99)
W rezultacie uzyskujemy:
1-sample proportions test with continuity correction
data: 350 out of 1000, null probability 0.5
X-squared = 89.401, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
99 percent confidence interval:
0.3117688 0.3902339
sample estimates:
p
0.35
Przedział od 31,1% do 39% z prawdopodobieństwem 0,99 pokrywa frakcję osób będących zwolennikami obecnego rządu.
Przykład 10.21
Korzystając z danych z przykładu 4.5 znaleźć przedział ufności dla frakcji osób, które przekroczyły granice Polski w 2006 roku celem dokonania zakupów.
Rozwiązanie:
W wiersz poleceń wpisujemy następujące polecenie:
> prop.test(200,400,conf.level=0.9)
Jako wynik uzyskujemy:
1-sample proportions test without continuity correction
data: 200 out of 400, null probability 0.5
X-squared = 0, df = 1, p-value = 1
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.459017 0.540983
sample estimates:
p
0.5
Przedział od 45,9% do 54,1% z prawdopodobieństwem 0,9 pokrywa frakcję osób, które
w 2006 roku przekroczyły granicę celem dokonania zakupów.
10.6. Minimalna liczebność próby
W programie R nie ma funkcji, które umożliwiałyby znalezienie minimalnej liczebności próby dla średniej bądź frakcji. Wykorzystując jednak podstawowe funkcje statystyczne operujące na wektorach i funkcje umożliwiające znalezienie odpowiednich kwantyli, w bardzo łatwy sposób można samodzielnie napisać program do wyznaczania minimalnej liczebności próby przy zadanym współczynniku ufności ![]()
oraz dopuszczalnym maksymalnym błędzie szacunku d.
10.6.1. Minimalna liczebność próby dla średniej
Przykład 10.22
Firma zajmująca się wyszukiwaniem stanowisk dla personelu kierowniczego chce oszacować średnią pensję, jaką może uzyskać pracownik pełniący funkcję kierowniczą na określonym szczeblu z dokładnością do 700 zł, przy 95% współczynniku ufności.
Z poprzednich badań wiadomo, że wariancja pensji personelu kierowniczego na tym szczeblu wynosi 40 000 000 zł2. Jaka jest minimalna wymagana liczebność próby?
Rozwiązanie:
Skorzystamy ze wzoru (4.22). Wpisujemy następujący fragment kodu:
> wariancja=40000000
> d=700
> z=qnorm(1-0.05/2,0,1)
> n=z^2*wariancja/d^2
> n
W efekcie uzyskujemy następujący wynik:
[1] 313.5885
Należy zatem wylosować co najmniej 314 osób pełniących funkcje kierownicze, aby przy współczynniku ufności 0,95 oszacować średnie wynagrodzenie takich osób z błędem nie większym niż 700 zł.
Przykład 10.23
Znajdź minimalną wymaganą liczebność próby do oszacowania średnich miesięcznych wydatków studentów na kino z błędem nie większym niż 5zł. Dla 10 losowo zapytanych studentów uzyskano następujące wyniki (w zł): 50, 70, 45, 35, 40, 50, 80, 85, 90, 40. Przyjmij współczynnik ufności ![]()
Rozwiązanie:
W pierwszej kolejności zapisujemy dane do wektora wydatki.
> wydatki=c(50,70,45,35,40,50,80,85,90,40)
Następnie wyznaczamy wartość odchylenia standardowego z próby wstępnej oraz wartość kwantyla i zapisujemy wyniki w zmiennych s i t odpowiednio. Ponadto, zmiennej d odnoszącej się do przyjętego w zadaniu maksymalnego dopuszczalnego błędu szacunku nadajemy wartość 5.
> s=sd(wydatki)
> t=qt(1-0.01/2,9)
> d=5
Wyznaczamy minimalną liczebność próby korzystając ze wzoru (4.23). W tym celu wydajemy polecenie:
> n=t^2*s^2/d^2
W rezultacie otrzymujemy wynik:
[1] 180.8352
Należy zatem zapytać się co najmniej 181 studentów o ich miesięczne wydatki na kino, aby oszacować średnie wydatki z błędem nie większym niż 5 zł przy współczynniku ufności 0,99 (bądź dolosować do 10 wstępnie już zapytanych 171 nowych studentów).
10.6.2. Minimalna liczebność próby dla frakcji
Przykład 10.24
Kandydat na prezydenta pewnego miasta chciałby wiedzieć jakiego poparcia mieszkańców może spodziewać się w najbliższych wyborach na fotel prezydenta. Ilu dorosłych mieszkańców tego miasta należy zapytać się o opinię na temat poparcia dla tego kandydata, aby przy współczynniku ufności 0,95 i maksymalnym dopuszczalnym błędzie szacunku 3% oszacować frakcję osób, które oddadzą głos na tego kandydata:
a) jeśli wiadomo, że kandydat ten w poprzednich wyborach uzyskiwał około 20% głosów,
b) jeśli kandydat startuje po raz pierwszy i nic nie wiadomo na temat poparcia dla niego wśród mieszkańców miasta.
Rozwiązanie:
a) Skorzystamy ze wzoru (4.24). W tym celu poszczególnym zmiennym przypisujemy następujące wartości:
> p=0.2
> d=0.03
> z=qnorm(1-0.05/2,0,1)
Następnie wpisujemy zgodnie ze wzorem (4.24) polecenie:
> n=z^2*p*(1-p)/d^2
> n
w rezultacie czego otrzymujemy:
[1] 682.926
Należy zatem zapytać się co najmniej 683 mieszkańców tego miasta aby oszacować frakcję popierających kandydata z błędem nie większym niż 3% i współczynniku ufności 0,95.
b) Skorzystamy ze wzoru (4.25). W tym celu poszczególnym zmiennym przypisujemy następujące wartości:
> p=0.5
> d=0.03
> z=qnorm(1-0.05/2,0,1)
Następnie wpisujemy zgodnie ze wzorem (4.25) polecenie:
> n=z^2/(4*d^2)
> n
w rezultacie czego otrzymujemy:
[1] 1067.072
W tym przypadku należy zapytać się co najmniej 1068 mieszkańców tego miasta aby oszacować frakcję popierających kandydata z błędem nie większym niż 3%
i współczynniku ufności 0,95.
10.7. Testowanie hipotez statystycznych
W programie R zaimplementowanych zostało wiele testów statystycznych, które omówione zostały w poprzednich podrozdziałach podręcznika. Dotyczy to zarówno testów parametrycznych, jak i nieparametrycznych. W podrozdziale tym pokażemy jak samodzielnie, a także wykorzystując funkcje wbudowane w programie R, zweryfikować odpowiednią hipotezę statystyczną. Przedstawione zostaną przy tym wybrane testy statystyczne.
10.7.1. Test dla jednej średniej
Przykład 10.25
Przypuszcza się, że średnie miesięczne zarobki pracowników pewnego dużego przedsiębiorstwa przekraczają 3000 zł brutto. Dla 8 losowo wybranych pracowników uzyskano następujące dane (w zł): 3500, 3200, 3000, 4000, 3300, 3800, 4200, 3400. Przyjmując, że rozkład płac pracowników jest normalny zweryfikuj tą hipotezę przyjmując ![]()
Rozwiązanie:
Zadanie rozwiążemy na 2 sposoby. W pierwszym, wykorzystamy podstawowe funkcje statystyczne operujące na wektorach. W drugim skorzystamy z funkcji t.test() wbudowanej w programie R, którą wykorzystaliśmy już do wyznaczenia przedziału ufności dla średniej.
I sposób:
Budujemy układ hipotez:
![]()
wobec ![]()
.
Dane zapisujemy do wektora placa.
> placa=c(3500,3200,3000,4000,3300,3800,4200,3400)
Następnie liczymy średnią płacę i odchylenie standardowe płacy z próby a wyniki zapisujemy do zmiennych srednia i s. Liczebność próby oznaczamy przez n.
> m0=3000
> n=length(placa)
> srednia=mean(placa)
> s=sqrt((n-1)/n)*sd(placa)
Wyznaczamy wartość statystyki testowej t-Studenta ze wzoru (6.7). W tym celu wpisujemy polecenie:
> t=(srednia-m0)/s*sqrt(n-1)
> t
w konsekwencji czego otrzymujemy wartość statystyki testowej t.
[1] 3.757215
Wyznaczamy wartość kwantyla w rozkładzie t-Studenta i zapisujemy ją do zmiennej tkr (mamy do czynienia z prawostronnym obszarem krytycznym więc jako prawdopodobieństwo podajemy ![]()
):
> tkr=qt(1-0.1,7)
> tkr
[1] 1.414924
Podobnie jak w przykładzie 10.14 zaznaczymy szarym kolorem obszar krytyczny. W tym celu wpisujemy w kolejne wiersze następujące polecenia:
> curve(dt(x,7),xlim=c(-4,4),ylim=c(0,0.4),ylab="f(x)",xlab="x")
> a=seq(qt(1-0.1,7),4,length=50)
> b=dt(a,7)
> polygon(c(a,rev(a)),c(rep(0,50),rev(b)),col="gray")
> text(1.41,-0.01,"1.41",cex=0.7)
> text(3.76,-0.01,"3.76",cex=0.7)
> text(2.25,0.01,"Obszar krytyczny",cex=0.7)
Na podstawie powyższego wykresu stwierdzamy, że hipotezę zerową należy odrzucić na korzyść hipotezy alternatywnej głoszącej, że średnie miesięczne zarobki pracowników przedsiębiorstwa przekraczają 3000 zł brutto.
II sposób:
W drugim podejściu wykorzystamy funkcję t.test(). W pierwszej jednak kolejności zdefiniujemy tzw. p-wartość (ang. p-value). Wynika to z faktu, że we wszystkich znanych pakietach statystycznych oprócz wartości statystyki testowej program zwraca tą właśnie wartość, dzięki której jesteśmy w stanie stwierdzić, czy hipotezę zerową należy odrzucić czy też nie.
Mianowicie, przez p-wartość należy rozumieć najmniejszy poziom istotności, przy którym hipotezę zerową należy odrzucić na korzyść hipotezy alternatywnej. Oznacza to, że jeżeli przyjęty w zadaniu poziom istotności ![]()
będzie spełniał warunek ![]()
to hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej. Jeżeli natomiast ![]()
to nie będzie podstaw do odrzucenia hipotezy zerowej.
Wpisujemy polecenie:
> t.test(placa,mu=3000,conf.level=0.9,alternative="greater")
w rezultacie czego otrzymujemy komunikat:
One Sample t-test
data: placa
t = 3.7572, df = 7, p-value = 0.003550
alternative hypothesis: true mean is greater than 3000
90 percent confidence interval:
3342.876 Inf
sample estimates:
mean of x
3550
Ponieważ przyjęty poziom istotności ![]()
jest większy od p-wartości, która wynosi p=0,00355 więc hipotezę zerową należy odrzucić na korzyść hipotezy alternatywnej. Zwróćmy uwagę, że w obydwu podejściach uzyskaliśmy taką samą wartość statystyki testowej t.
Przykład 10.26
Korzystając z danych z przykładu 6.1 zweryfikować hipotezę, że średnie przychody ze sprzedaży w małych firmach pewnej branży w roku 2008 wyniosły 6,4 mln zł.
Rozwiązanie:
Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
![]()
.
W programie R w przypadku, gdy liczebność próby ![]()
należy samodzielnie obliczyć wartość statystyki z w teście dla jednej średniej.
W pierwszym etapie tworzymy wektory zawierające środki kolejnych przedziałów oraz ich liczebności.
> srodek=c(2,4,6,8,10,12)
> liczebnosc=c(10,23,40,15,8,4)
> n=sum(liczebnosc)
Liczymy średnie przychody ze sprzedaży:
> srednia=sum(srodek*liczebnosc)/n
Liczymy odchylenie standardowe przychodów ze sprzedaży:
> s=(sum((srodek-srednia)^2*liczebnosc)/n)^0.5
oraz wartość statystyki testowej z:
> z=(srednia-6.4)/s*sqrt(49)
> z
[1] -1.158648
Wyznaczamy wartość krytyczną i zapisujemy ją do zmiennej zkr:
> zkr=qnorm(1-0.05/2,0,1)
> zkr
[1] 1.959964
Celem graficznego przedstawienia obszaru krytycznego wydajemy następujące komendy:
> curve(dnorm(x,0,1),xlim=c(-3,3),ylim=c(0,0.4),ylab="f(x)",xlab="x")
> a1=seq(-3,-qnorm(1-0.05/2,0,1),length=50)
> a2= seq(qnorm(1-0.05/2,0,1),3,length=50)
> b1=dnorm(a1,0,1)
> b2=dnorm(a2,0,1)
> polygon(c(a1,rev(a1)),c(rep(0,50),rev(b1)),col="gray")
> polygon(c(a2,rev(a2)),c(rep(0,50),rev(b2)),col="gray")
> polygon(c(-qnorm(1-0.05/2),qnorm(1-0.05/2)),c(0,0))
> text(1.96,-0.01,"1.96",cex=0.7)
> text(-1.96,-0.01,"-1.96",cex=0.7)
> text(-1.16,-0.01,"-1.16",cex=0.7)
W rezultacie otrzymujemy następujący rysunek.
Nie ma zatem podstaw do odrzucenia hipotezy zerowej, że średnie przychody ze sprzedaży w małych firmach badanej branży wynosiły w 2008 roku 6,4 mln zł.
10.7.2. Test dla dwóch średnich
Przykład 10.27
Korzystając z danych z przykładu 6.3 zweryfikować hipotezę, że płynność finansowa firm w branży A jest większa niż firm w branży B.
Rozwiązanie:
Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
![]()
,
gdzie ![]()
i ![]()
oznaczają średnią płynność finansową wszystkich firm z branży A i B odpowiednio.
W programie R do weryfikacji hipotezy o równości dwóch średnich służy funkcja t.test() - podobnie jak w przypadku testu dla jednej średniej. Funkcja ta umożliwia przeprowadzenie testu dla dwóch średnich zarówno przy założeniu równej wariancji, jak
i przy braku tego założenia (opcja domyślna). W przypadku, gdy wariancje są różne, wykorzystywana jest poprawka Welcha. W pierwszej kolejności zweryfikujemy hipotezę
o równości wariancji. Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
wobec ![]()
.
W tym celu wykorzystamy funkcję var.test().
> var.test(branzaA,branzaB)
W rezultacie otrzymujemy następujący wynik:
F test to compare two variances
data: branzaA and branzaB
F = 0.381, num df = 7, denom df = 6, p-value = 0.2326
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.0668869 1.9499416
sample estimates:
ratio of variances
0.3809524
Ponieważ przyjęty poziom istotności ![]()
jest mniejszy od p-wartości to nie mamy podstaw do odrzucenia hipotezy zerowej o równości wariancji. Testując zatem hipotezę
o równości dwóch średnich należy zmienić domyślną opcję o braku równości wariancji
w populacjach generalnych.
Wpisujemy następującą komendę:
> t.test(branzaA,branzaB,var.equal=TRUE)
W rezultacie otrzymujemy następujący wynik:
Two Sample t-test
data: branzaA and branzaB
t = -0.6831, df = 13, p-value = 0.7467
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-0.3592381 Inf
sample estimates:
mean of x mean of y
0.7 0.8
Ponieważ przyjęty poziom istotności ![]()
jest mniejszy od p-wartości to nie mamy podstaw do odrzucenia hipotezy zerowej o równości średnich.
W przypadku gdy obydwie próby są duże należy samodzielnie wyznaczyć wartość statystyki testowej ze wzoru (6.13). Podobnie należy postąpić, gdy znane są odchylenia standardowe ![]()
w obydwu populacjach generalnych (6.12). Należy się wówczas wzorować na rozwiązaniu wcześniejszych przykładów.
10.7.3. Test dla jednej frakcji
Przykład 10.28
Wysunięto hipotezę, że mniej niż 10% studentów UE w Poznaniu jest niezadowolonych
z jakości kształcenia na uczelni. Zapytano 200 losowo wybranych studentów o ich opinię
i okazało się, że wśród nich 10 negatywnie ocenia jakość kształcenia. Przyjmując poziom istotności ![]()
zweryfikuj tą hipotezę.
Rozwiązanie:
Test dla wskaźnika bądź dwóch wskaźników struktury został zaimplementowany w R
w postaci funkcji prop.test() i oparty został na statystyce mającej rozkład ![]()
(testowanie hipotez dla jednej bądź dwóch frakcji, które przedstawiono w rozdziale 6 oparto o statystyki testowe mające rozkład N(0,1)).
Układ hipotez jest postaci:
![]()
wobec ![]()
> prop.test(10,200,0.1,alternative="less",conf.level=0.9)
W rezultacie otrzymujemy następujący wynik:
1-sample proportions test with continuity correction
data: 10 out of 200, null probability 0.1
X-squared = 5.0139, df = 1, p-value = 0.01257
alternative hypothesis: true p is less than 0.1
90 percent confidence interval:
0.00000000 0.07660087
sample estimates:
p
0.05
Ponieważ przyjęty w zadaniu poziom istotności ![]()
jest większy od p-wartości hipotezę zerową należy odrzucić na korzyść hipotezy alternatywnej. Oznacza to, że mniej niż 10% studentów UE jest niezadowolonych z jakości kształcenia.
10.7.4. Test dla dwóch frakcji
Przykład 10.29
Wysunięto przypuszczenie, że maszyna A jest lepsza od maszyny B. Na 500 losowo wybranych i wyprodukowanych przez maszynę A detali, 10 okazało się być brakami. Natomiast na 700 losowo wybranych i wyprodukowanych przez maszynę B brakami było 30. Przyjmując ![]()
zweryfikuj tą hipotezę.
Rozwiązanie:
Oznaczmy przez ![]()
i ![]()
frakcję braków produkowanych przez maszynę A i B odpowiednio. Układ hipotez jest postaci:
![]()
wobec ![]()
> prop.test(c(10,30),c(500,700),alternative="less")
W rezultacie otrzymujemy następujący wynik:
2-sample test for equality of proportions with continuity correction
data: c(10, 30) out of c(500, 700)
X-squared = 4.0463, df = 1, p-value = 0.02213
alternative hypothesis: less
95 percent confidence interval:
-1.000000000 -0.004876213
sample estimates:
prop 1 prop 2
0.02000000 0.04285714
Ponieważ przyjęty w zadaniu poziom istotności ![]()
jest większy od p-wartości hipotezę zerową należy odrzucić na korzyść hipotezy alternatywnej głoszącej, że maszyna A jest lepsza od maszyny B.
10.7.5. Test dla wariancji
Przykład 10.30
Korzystając z danych z przykładu 6.5 sprawdź, czy jest możliwe, że przeciętne zróżnicowanie rotacji należności (w dniach) w małych firmach w Poznaniu przekroczyło w roku 2008 ± 4 dni.
Rozwiązanie:
Zadanie rozwiążemy korzystając z funkcji opisanych w poprzednich podrozdziałach. Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
wobec ![]()
.
Zebrane dane zapisujemy do wektora rotacja a liczebność próby do zmiennej n.
> rotacja=c(28,20,18,16,10,8,19,10,9,12)
> n=length(rotacja)
Liczymy wariancję z próby i zapisujemy ją do zmiennej wariancja:
> wariancja=(n-1)/n*var(rotacja)
> wariancja
[1] 36.4
Liczymy wartość statystyki testowej ze wzoru (6.21) i zapisujemy ją do zmiennej chi.
> chi=n*wariancja/16
> chi
[1] 22.75
Dla poziomu istotności 0,05 i 9 stopni swobody wyznaczamy wartość krytyczną.
> qchisq(1-0.05,9)
[1] 16.91898
Sporządzamy rysunek funkcji gęstości zmiennej losowej o rozkładzie ![]()
z 9 stopniami swobody, zaznaczając obszar krytyczny i wartość statystyki testowej.
> curve(dchisq(x,9),xlim=c(0,25),ylim=c(0,0.12),ylab="f(x)",xlab="x")
> a=seq(qchisq(1-0.05,9),25, length=50)
> b=dchisq(a,9)
> polygon(c(a,rev(a)),c(rep(0,50),rev(b)),col="gray")
> polygon(c(0,qchisq(1-0.05,9)),c(0,0))
> text(16.92,-0.001,"16.92",cex=0.7)
> text(22.75,-0.001,"22.75 ",cex=0.7)
Ponieważ zachodzi relacja:![]()
, więc H0 odrzucamy na korzyść H1. Oznacza to, że przeciętne zróżnicowanie rotacji należności w małych firmach
w Poznaniu przekracza 4 dni.
10.7.6. Test dla dwóch wariancji
Przykład 10.31
Sprawdź, przy poziomie istotności = 0,05, czy zmienność plonów pszenicy
w gospodarstwach rolnych w województwie lubelskim jest wyższa niż
w zachodniopomorskim, jeżeli z prób otrzymano następujące wyniki (w q/ha):
woj. lubelskie: 40, 36, 28, 30, 32, 28, 42, 44.
woj. zachodniopomorskie: 38, 36, 30, 27, 25, 40.
Rozwiązanie:
W rozwiązaniu tego zadania wykorzystamy funkcję var.test(), którą można zastosować do weryfikacji hipotezy o jednorodności wariancji.
Stawiamy hipotezy:
![]()
wobec ![]()
,
gdzie ![]()
oznacza wariancję plonów pszenicy w gospodarstwach rolnych
w województwie lubelskim, a ![]()
wariancję plonów pszenicy w gospodarstwach rolnych w województwie zachodniopomorskim.
Zebrane dane zapisujemy do wektorów plony_lub i plony_zach:
> plony_lub=c(40,36,28,30,32,28,42,44)
> plony_zach=c(38,36,30,27,25,40)
Następnie wykorzystujemy funkcję var.test():
> var.test(plony_lub,plony_zach,alternative="greater")
w efekcie czego otrzymujemy następujący wynik:
F test to compare two variances
data: plony_lub and plony_zach
F = 1.0752, num df = 7, denom df = 5, p-value = 0.4853
alternative hypothesis: true ratio of variances is greater than 1
95 percent confidence interval:
0.2205066 Inf
sample estimates:
ratio of variances
1.075162
Ponieważ przyjęty w zadaniu poziom istotności ![]()
jest mniejszy od p-wartości więc nie ma podstaw do odrzucenia hipotezy zerowej o równości wariancji plonów w obydwu województwach.
10.7.7. Test dla mediany
Przykład 10.32
Korzystając z danych z przykładu 6.9, zweryfikuj hipotezę, że mediana wydajności pracy pracowników firmy wynosi 109%.
Rozwiązanie:
Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
wobec ![]()
Zebrane dane zapisujemy do wektora wydajnosc:
>wydajnosc=c(105,107,103,120,111,95,98,100,115,117,106,93,97,100,112,118,104,99,125,113,96,107,110,110,103)
Liczymy jednostki, dla których wartość cechy przekracza 109. W tym celu skorzystamy
z funkcji sum():
> f1=sum(wydajnosc>109)
> f1
[1] 10
Wyznaczamy wartość statystyki t ze wzoru (6.38).
> t=(2*f1-length(wydajnosc))/sqrt(length(wydajnosc))
> t
[1] -1
Wyznaczamy wartość krytyczną dla ![]()
i liczby stopni swobody wynoszącej ∞.
> tkr=qt(1-0.05/2,Inf) # Inf symbolizuje nieskończoność
> tkr
[1] 1.959964
Celem graficznego przedstawienia obszaru krytycznego wydajemy następujące komendy:
> curve(dt(x,Inf),xlim=c(-3,3),ylim=c(0,0.4),ylab="f(x)",xlab="x")
> a1=seq(-3,-qt(1-0.05/2,Inf),length=50)
> a2= seq(qt(1-0.05/2,Inf),3,length=50)
> b1=dt(a1,Inf)
> b2=dt(a2,Inf)
> polygon(c(a1,rev(a1)),c(rep(0,50),rev(b1)),col="gray")
> polygon(c(a2,rev(a2)),c(rep(0,50),rev(b2)),col="gray")
> polygon(c(-qt(1-0.05/2,Inf),qt(1-0.05/2,Inf)),c(0,0))
> text(1.96,-0.01,"1.96",cex=0.7)
> text(-1.96,-0.01,"-1.96",cex=0.7)
> text(-1,-0.01,"-1",cex=0.7)
Analiza wykresu sugeruje, że nie ma podstaw do odrzucenia hipotezy zerowej głoszącej, że mediana wydajności pracy pracowników wynosi 109%.
10.7.8. Test ![]()
zgodności
Przykład 10.33
Korzystając z danych przykładu 7.1 zweryfikuj przypuszczenie, że absencja pracowników w przedsiębiorstwie W jest taka sama w poszczególnych dniach tygodnia.
Rozwiązanie:
Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
wobec ![]()
gdzie ![]()
oznacza dystrybuantę rozkładu równomiernego.
W programie R test ![]()
na zgodność rozkładu jest zaimplementowany pod funkcją chisq.test(). W przypadku wnioskowania zgodności z pewnym rozkładem teoretycznym pierwszy wektor zawiera dane, a drugi prawdopodobieństwa ich wystąpienia w testowanym rozkładzie.
Dane zapisujemy do zmiennej absencja, a prawdopodobieństwa do zmiennej pr.
> absencja=c(28,13,20,15,24)
> pr=rep(1/5,5)
Następnie wpisujemy polecenie:
> chisq.test(absencja,p=pr)
otrzymując w wyniku:
Chi-squared test for given probabilities
data: absencja
X-squared = 7.7, df = 4, p-value = 0.1032
Ponieważ przyjęty w zadaniu poziom istotności jest mniejszy od p-wartości to oznacza to, że nie ma podstaw do odrzucenia hipotezy zerowej, że absencja jest taka sama we wszystkich dniach tygodnia.
10.7.9. Test ![]()
niezależności
Przykład 10.34
W salonach samochodowych jednej z wiodących na rynku marek przeprowadzono badanie, którego celem było sprawdzenie czy kolor kupowanego auta zależy od płci kupującego. Uzyskano następujące wyniki:
Kolor |
Płeć |
|
|
Mężczyzna |
Kobieta |
Czerwony |
100 |
100 |
Czarny |
50 |
350 |
Srebrny |
350 |
50 |
Źródło: dane umowne.
Czy kolor kupowanego auta zależy od płci kupującego? Przyjmij ![]()
Rozwiązanie:
Stawiamy hipotezę zerową i alternatywną:
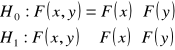
W programie R test ![]()
niezależności został zaimplementowany, podobnie jak test ![]()
zgodności, pod funkcją chisq.test(). W pierwszej kolejności tworzymy wektory, które zawierać będą informacje o liczbie zakupionych aut przez mężczyzn i kobiety
z uwzględnieniem kolorów aut. Następnie wykorzystując funkcję cbind() tworzymy tabelę zawierającej liczebności empiryczne.
> m=c(100,50,350)
> k=c(100,350,50)
> tabela=cbind(m,k)
Wywołujemy funkcję chisq.test().
>chisq.test(tabela)
Uzyskujemy następujący komunikat.
Pearson's Chi-squared test
data: tabela
X-squared = 450, df = 2, p-value < 2.2e-16
Ponieważ przyjęty w zadaniu poziom istotności ![]()
jest większy od p-wartości, hipotezę zerową o niezależności badanych cech należy odrzucić na korzyść hipotezy alternatywnej.
10.7.10. Test Kołmogorowa-Smirnowa
Przykład 10.35
Zweryfikuj hipotezę, że zysk operacyjny (w tys. zł) w dwóch przedsiębiorstwach A i B ma taki sam rozkład, jeśli w wybranych siedmiu miesiącach 2008 roku kształtował się on następująco:
Przedsiębiorstwo „A” |
11,24 |
12,02 |
9,06 |
10,82 |
14,71 |
13,03 |
7,49 |
Przedsiębiorstwo „B” |
9,81 |
9,25 |
7,99 |
7,64 |
10,38 |
9,32 |
12,50 |
Źródło: dane umowne.
Przyjmij = 0,05. Zastosuj test Kołmogorowa-Smirnowa.
Rozwiązanie:
Stawiamy hipotezę zerową i alternatywną:
![]()
wobec ![]()
.
Dane dla obydwu przedsiębiorstw zapisujemy do zmiennych A i B odpowiednio.
> A=c(11.24,12.02,9.06,10.82,14.71,13.03,7.49)
> B=c(9.81,9.25,7.99,7.64,10.38,9.32,12.50)
Następnie w linię komend wpisujemy:
> ks.test(A,B)
otrzymując:
Two-sample Kolmogorov-Smirnov test
data: A and B
D = 0.5714, p-value = 0.2121
alternative hypothesis: two-sided
Oznacza to, że przy przyjętym poziomie istotności ![]()
nie ma podstaw do odrzucenia hipotezy zerowej.
10.7.11. Test Shapiro-Wilka
Przykład 10.36
Korzystając z danych z przykładu 7.7 zweryfikuj hipotezę, że rozkład ROE
w przedsiębiorstwach pewnej branży jest normalny. Przyjmij ![]()
.
Rozwiązanie:
Stawiamy hipotezę zerową i alternatywną:
![]()
wobec ![]()
.
Dane dla przedsiębiorstw zapisujemy do zmiennej ROE:
> ROE=c(18,26,33,48,42,13,24,30,45,37)
Następnie w linię komend wpisujemy:
> shapiro.test(ROE)
otrzymując:
Shapiro-Wilk normality test
data: ROE
W = 0.9715, p-value = 0.9044
Oznacza to, że nie ma podstaw do odrzucenia H0, która mówi, że rozkład ROE jest normalny.
10.7.12. Testy istotności dla współczynnika korelacji liniowej Pearsona
Przykład 10.37
Korzystając z danych z przykładu 8.1 zweryfikuj hipotezę o istotności współczynnika korelacji liniowej Pearsona pomiędzy wydajnością pracy a stażem pracy. Przyjmij ![]()
.
Rozwiązanie:
Stawiamy hipotezę zerową i alternatywną:
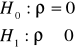
Informacje o stażu i wydajności zapisujemy do zmiennych staz i wydajnosc.
> staz=c(1,2,3,4,5,6,7,8,9,10)
> wydajnosc=c(10,15,13,19,23,20,18,25,15,22)
Do weryfikacji hipotezy o istotności współczynnika korelacji liniowej Pearsona służy
w programie R funkcja cor.test().
> cor.test(staz,wydajnosc,method="pearson")
W rezultacie uzyskujemy następujący komunikat:
Pearson's product-moment correlation
data: staz and wydajnosc
t = 2.2792, df = 8, p-value = 0.05214
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.00358983 0.90109329
sample estimates:
cor
0.6274547
Funkcja dostarcza szereg informacji: wartość statystyki testowej (wzór 8.4), liczbę stopni swobody, p-wartość, przedział ufności dla współczynnika korelacji liniowej Pearsona oraz jego ocenę z próby.
Ponieważ przyjęty w zadaniu poziom istotności ![]()
jest mniejszy od p-wartości, to oznacza to, że nie ma podstaw do odrzucenia hipotezy zerowej głoszącej, że współczynnik korelacji liniowej Pearsona jest statystycznie nieistotny.
10.7.13. Testy istotności dla współczynnika regresji liniowej
Przykład 10.38
Badano relację między przeciętnym miesięcznym dochodem rozporządzalnym na 1 osobę w gospodarstwach domowych (w złotych) a przeciętnymi miesięcznymi wydatkami na kulturę, sport i wypoczynek (na 1 osobę w zł) w gospodarstwach ogółem. Dla wybranych 10 województw uzyskano następujące dane:
Dochód (X) |
Wydatki na kulturę, sport i wypoczynek (Y) |
536 |
32,7 |
417 |
13,5 |
469 |
20,8 |
475 |
24,5 |
507 |
30,9 |
429 |
19,7 |
435 |
17,7 |
484 |
23,4 |
459 |
17,9 |
490 |
27,9 |
Źródło: dane umowne.
Wyznacz liniową funkcję regresji wydatków na kulturę, sport i wypoczynek względem dochodu. Czy na poziomie istotności ![]()
współczynnik kierunkowy jest istotny statystycznie?
Rozwiązanie:
Informacje o dochodzie i wydatkach zapisujemy do zmiennych dochod i wydatki.
> dochod=c(536,417,469,475,507,429,435,484,459,490)
> wydatki=c(32.7,13.5,20.8,24.5,30.9,19.7,17.7,23.4,17.9,27.9)
W dalszej kolejności sporządzamy diagram korelacyjny, którego analiza ułatwi dobór odpowiedniego modelu regresji. W tym celu korzystamy z funkcji plot(), która służy m.in. do tworzenia wykresu punktowego.
> plot(dochod,wydatki)
Dokonując wzrokowej analizy można przyjąć, że uzasadniony jest wybór liniowej funkcji regresji. Do szacowania parametrów modelu regresji liniowej służy funkcja lm() (skrót
z języka angielskiego od linear model). Zapisujemy wyniki estymacji w zmiennej model. W tym celu wpisujemy następujące polecenie:
> model=lm(wydatki~dochod)
> model
uzyskując:
Call:
lm(formula = wydatki ~ dochod)
Coefficients:
(Intercept) dochod
-51.4299 0.1581
W ten sposób uzyskaliśmy oceny wyrazu wolnego (-51,4) oraz współczynnika kierunkowego (0,158).
Wykorzystując funkcję abline() możemy dodać do wykresu prostą o zadanych parametrach, w tym przypadku pobranych z obiektu model.
> abline(model)
Celem zweryfikowania czy współczynnik kierunkowy jest istotny statystycznie budujemy następujący układ hipotez statystycznych:
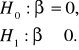
Chcąc uzyskać więcej informacji o modelu należy wykorzystać funkcję summary().
> summary(model)
W ten sposób uzyskujemy następujący komunikat:
Call:
lm(formula = wydatki ~ dochod)
Residuals:
Min 1Q Median 3Q Max
-3.2449 -1.5244 -0.1350 1.5964 3.2985
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -51.42989 9.34745 -5.502 0.000572 ***
dochod 0.15812 0.01983 7.974 4.47e-05 ***
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.189 on 8 degrees of freedom
Multiple R-Squared: 0.8882, Adjusted R-squared: 0.8743
F-statistic: 63.58 on 1 and 8 DF, p-value: 4.471e-05
W rezultacie wywołania funkcji summary() na zmiennej model otrzymujemy kompleksową informację na temat liniowej funkcji regresji. Są tu informacje na temat reszt modelu (najmniejsza i największa reszta oraz kwartyle reszt), oceny parametrów modelu wraz z ich średnimi błędami szacunków oraz wartość statystyki testowej służącej do sprawdzenia czy odpowiednie parametry modelu są statystycznie istotne. Podana jest ponadto p-wartość oraz występujące obok niej „kody istotności”, które informują od jakiego poziomu istotności parametry modelu regresji są statystycznie istotne. W naszym przypadku '***' oznaczają, że zarówno współczynnik kierunkowy, jak i wyraz wolny są statystycznie istotne dla każdego poziomu istotności równego co najmniej 0,001. Komunikat zawiera ponadto informacje o odchyleniu standardowym składnika resztowego, współczynniku determinacji oraz skorygowanym współczynniku determinacji. Zawarta jest również wartość statystyki F służącej do weryfikacji hipotezy o istotności współczynnika korelacji wielorakiej.
Z przeprowadzonych rozważań wynika, że przy poziomie istotności ![]()
hipotezę zerową o tym, że współczynnik kierunkowy nie jest istotny statystycznie należy odrzucić.
Przykład 10.39
Korzystając z danych z przykładu 9.4 sprawdzić czy współczynnik kierunkowy liniowej funkcji trendu liczby upadłości firm w Niemczech jest istotny statystycznie. Przyjąć ![]()
.
Rozwiązanie:
Funkcję lm() można również wykorzystać do wyznaczenia parametrów liniowej funkcji trendu i weryfikacji hipotezy o istotności współczynnika kierunkowego. Dane o liczbie upadłości w Niemczech w latach 1999-2007 zapisujemy do zmiennej upadlosc. Tworzymy dodatkowo wektor, który zawierać będzie ponumerowane kolejnymi liczbami naturalnymi lata 1999-2007.
> upadlosc=c(33.9,41.8,49.5,84.3,100.4,118.3,136.6,154.9,167.0)
> lata=c(1:length(upadlosc))
Stawiamy hipotezy: ![]()
, ![]()
Następnie wykorzystując funkcję lm() wpisujemy polecenie:
> model=lm(upadlosc~lata)
> summary(model)
Uzyskujemy następujący komunikat:
Call:
lm(formula = upadlosc ~ lata)
Residuals:
Min 1Q Median 3Q Max
-13.026 -2.727 1.878 2.383 7.371
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.5306 4.5514 1.874 0.103
lata 17.9983 0.8088 22.253 9.36e-08 ***
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.265 on 7 degrees of freedom
Multiple R-Squared: 0.9861, Adjusted R-squared: 0.9841
F-statistic: 495.2 on 1 and 7 DF, p-value: 9.357e-08
Oznacza to, że na poziomie istotności ![]()
hipotezę zerową mówiącą o tym, że współczynnik kierunkowy liniowej funkcji trendu nie jest istotny statystycznie należy odrzucić. Wyznaczoną funkcję trendu można też zaprezentować na wykresie:
> plot(lata,upadlosc,main="Upadłości firm w Niemczech w latach 1999-2007",xlab="Lata",ylab="tys",sub="Źródło: Opracowanie własne")
> abline(model)
> text(6,100,"y=18t+8,53")
10.8. Zadania
Zadanie 10.1
Korzystając z funkcji wbudowanych w R policz wybrane statystyki opisowe wzrostu 12 studentów ( w cm): 172, 176, 190, 186, 165, 169, 172, 178, 179, 184, 164,165.
Zadanie 10.2
Wygeneruj 100 obserwacji z rozkładu normalnego N(20,4) opisującego zysk ( w tys. zł) 100 przedsiębiorstw pewnej branży. Oblicz wybrane statystyki opisowe.
Zadanie 10.3
Załóżmy, że zmienna losowa X ma rozkład normalny N(50,5). Oblicz:
a) P(X<54),
b) P(X>69),
c) P(45<X<55),
d) wszystkie kwartyle.
Zadanie 10.4
Dana jest zmienna losowa X podlegająca rozkładowi normalnemu N(10,2). Znaleźć prawdopodobieństwo, że przyjmie ona wartość:
a) należącą do przedziału (5,8),
b) większą od 7,
c) nie większą od 12.
Zaznacz te prawdopodobieństwa wykorzystując wykres funkcji gęstości.
Zadanie 10.5
Załóżmy, że miesięczny zysk przedsiębiorstwa (w tys. zł) ma rozkład normalny N(70,15).
a) sporządź wykres funkcji gęstości tej zmiennej losowej,
b) jakie jest prawdopodobieństwo, że w najbliższym miesiącu zysk przedsiębiorstwa przekroczy 80 tys. zł,
c) jakie jest prawdopodobieństwo, że w najbliższym miesiącu zysk przedsiębiorstwa nie przekroczy 65 tys. zł,
d) jakie jest prawdopodobieństwo, że w najbliższym miesiącu zysk przedsiębiorstwa będzie od 60 tys. zł do 80 tys. zł.
Zadanie 10.6
Wiedząc, że zmienna losowa Z~N(0,1) oblicz oraz przedstaw graficznie:
a) P(0 < Z < 3),
b) P(Z < -0,5),
c) P(Z > 1).
Zadanie 10.7
Oblicz wszystkie kwartyle w rozkładzie t-Studenta z 5 stopniami swobody.
Zadanie 10.8
Znaleźć kwantyl rzędu 0,95 w rozkładzie:
a) N(100,10)
b) t(12)
c) ![]()
d) F(12,5)
Zadanie 10.9
Wygenerować po 10 obserwacji z rozkładu:
a) N(30,5),
b) t(10),
c) ![]()
,
d) F(10,5).
Zadanie 10.10
Sporządzić wykresy funkcji gęstości zmiennych losowych o rozkładzie:
a) N(10,3),
b) t(7),
c) ![]()
,
d) F(10,9).
Zadanie 10.11
Na jednym rysunku sporządzić wykresy funkcji gęstości zmiennej losowej X~N(0,1) oraz Y~t(5).
Zadanie 10.12
Sporządzić wykres dystrybuanty zmiennej losowej o rozkładzie t-Studenta z 7 stopniami swobody.
Zadanie 10.13
Obliczyć kwantyl rzędu 0,9 w rozkładzie normalnym standaryzowanym oraz przedstawić jego interpretację geometryczną na wykresie odpowiedniej funkcji gęstości.
Zadanie 10.14
Obliczyć kwantyl rzędu 0,99 w rozkładzie normalnym standaryzowanym oraz przedstawić jego interpretację geometryczną na wykresie dystrybuanty.
Zadanie 10.15
Pobrano próbę 15 studentów i zbadano ich wzrost. Otrzymano następujące wyniki (cm): 165, 180, 180, 175, 177, 195, 170, 182, 187, 173, 178, 190, 188, 175, 182. Zbuduj 99% przedział ufności dla średniego wzrostu wszystkich studentów.
Zadanie 10.16
Dyrektor jednej z poznańskich rozgłośni radiowych zlecił badania mające na celu określenie przedziału dla średniego wieku słuchaczy radia. Wiek losowo wybranych 8 słuchaczy tego radia (w latach) przedstawia się następująco: 30; 35; 40; 39; 37; 35; 39; 32. Wyznacz 90% przedział ufności dla średniego wieku słuchacza tego radia.
Zadanie 10.17
Znajdź minimalną wymaganą liczebność próby (liczbę dni w ciągu których należy przeprowadzać badanie) do oszacowania przeciętnej liczby koszul sprzedawanych dziennie w pewnym sklepie z dokładnością do 2 sztuk, przy 90% współczynniku ufności, jeżeli
w ciągu 10 dni sprzedano następującą liczbę koszul: 50, 54, 56, 45, 67, 54, 58, 76, 53,67.
Zadanie 10.18
Wylosowano próbę składającą się z 10 pracowników pewnego zakładu Z i zbadano ich staż pracy (w latach). Kształtował się on następująco: 1,3,4,5,5,6,7,8,9,12. Czy na podstawie tych obserwacji można twierdzić, że średni staż pracy wszystkich pracowników zatrudnionych w zakładzie Z jest mniejsze od 7 lat? Przyjąć poziom istotności 0,05.
Zadanie 10.19
Testy pewnego modelu samochodu, który miał właśnie wejść na rynek miały wykazać jego ekonomiczność w tym sensie, że średnie zużycie paliwa na 100 km miało nie przekraczać 6,2 l/100 km. Wylosowano 15 pojazdów, z których każdy przejechał około 1000 km
w różnych warunkach klimatyczno - drogowych i otrzymano następujące wyniki:
7,11; 6,28; 5,95; 7,21; 5,99; 6,89; 7,25; 7,13; 6,03; 5,90; 6,77; 6,02; 6,45; 5,85; 7,20
Na poziomie istotności 0,05 oceń ekonomiczność tego modelu.
Zadanie 10.20
Zdaniem kierownika zmiany, maszyna produkująca pewne elementy wymaga naprawy. Norma dla tego typu maszyny mówi, że w długiej partii wyprodukowanych towarów procent braków może wynosić 3%. W partii 500 losowo wybranych elementów 40 było wadliwych. Czy na tej podstawie rzeczywiście kierownik zmiany powinien oddać maszynę do naprawy? Przyjmij poziom istotności 0,05.
Zadanie 10.21
W Poznaniu wylosowano 200 kobiet i 150 mężczyzn pytając ich, czy są zadowoleni z prac obecnego rządu. Odpowiedzi pozytywnej udzieliło 48 kobiet i 45 mężczyzn. Na poziomie istotności 0,01 zweryfikuj hipotezę, że istnieje zgodność opinii kobiet i mężczyzn w tym względzie.
Zadanie 10.22
Zdaniem kierownika zmiany maszyna A jest gorsza od maszyny B. Na 500 elementów wyprodukowanych przez maszynę A 50 miało usterki, a na 1000 wyprodukowanych przez maszynę B było 40 usterek. Czy to przypuszczenie kierownika jest uzasadnione? Przyjmij poziom istotności 0,05.
Zadanie 10.23
Pewną monetą wykonano 1000 rzutów i okazało się, że orzeł wypadł 400 razy a reszka 600. Czy na poziomie istotności 0,05 można uważać, że moneta jest symetryczna? Zastosuj odpowiedni test.
Zadanie 10.24
Pewien hazardzista, który bardzo często chodzi do kasyna „I tak nie wygrasz” zaobserwował, że w jednej z jego ulubionych gier używana jest „trefna” kostka. W ciągu kolejnych 600 rzutów wykonanych tą kostką zaobserwował następującą liczbę oczek:
Liczba oczek |
Liczba rzutów |
1 |
100 |
2 |
150 |
3 |
150 |
4 |
70 |
5 |
80 |
6 |
50 |
Suma |
600 |
Źródło: dane umowne.
Czy na poziomie istotności 0,01 hazardzista może uważać, że w kasynie, w jego ulubionej grze, używa się niesymetrycznej kostki?
Zadanie 10.25
Pogrupowano 200 wylosowanych dorosłych osób uczestniczących w badaniu socjologicznym jednocześnie według poziomu dochodu i orientacji politycznej.
Dochód |
Orientacja polityczna |
||
|
Lewicowa |
Centrowa |
Prawicowa |
Niski Średni Wysoki |
40 14 21 |
26 44 15 |
10 18 12 |
Źródło: dane umowne.
Czy występuje zależność między statusem materialnym a orientacją polityczną? Przyjmij poziom istotności 0,05.
Zadanie 10.26
W pewnym badaniu dotyczącym najchętniej oglądanych przez Polaków programów
uzyskano poniższe dane.
Płeć |
Najchętniej oglądane programy |
|
|
Seriale |
Sport |
Kobieta Mężczyzna |
56 30 |
14 100 |
Źródło: dane umowne.
Przyjmując ![]()
zweryfikuj hipotezę, że rodzaj oglądanego najchętniej programu nie zależy od płci telewidza.
Zadanie 10.27
Zweryfikuj hipotezę, że ponoszone przez dwa przedsiębiorstwa P1 i P2 miesięczne koszty (w tys. zł) ich działalności mają taki sam rozkład, jeśli w wybranych siedmiu miesiącach 2008 roku kształtowały się one następująco:
P1 |
113,24 |
120,32 |
93,66 |
102,42 |
130,71 |
125,03 |
71,34 |
P2 |
92,61 |
91,50 |
73,89 |
72,34 |
110,38 |
93,32 |
120,22 |
Źródło: dane umowne.
Przyjmij = 0,05. Zastosuj test Kołmogorowa-Smirnowa.
Zadanie 10.28
Miesięczny zysk (w tys. zł) pewnego przedsiębiorstwa kształtował się w 8 wybranych miesiącach w następujący sposób.
Zysk |
13,9 |
13,3 |
14,2 |
17 |
13,6 |
17,9 |
18,8 |
12,2 |
Źródło: dane umowne.
Zweryfikuj hipotezę, że rozkład zysku w przedsiębiorstwie jest normalny. Przyjmij ![]()
. Zastosuj test Shapiro-Wilka.
Zadanie 10.29
Poziom zatrudnienia (w tys. osób) oraz wielkość produkcji (w tys. ton) w ośmiu przedsiębiorstwach przemysłowych kształtowały się następująco:
Zatrudnienie |
0,9 |
1 |
1,2 |
1,2 |
1,4 |
1,4 |
1,5 |
1,6 |
Produkcja |
2 |
2,3 |
2,6 |
2,5 |
3 |
3,1 |
3,2 |
3,4 |
Źródło: dane umowne.
a) Oblicz współczynnik korelacji liniowej Pearsona i go zinterpretuj.
b) Przyjmując poziom istotności 0,01 zweryfikuj hipotezę o istotności współczynnika korelacji liniowej Pearsona.
c) Na poziomie istotności 0,05 zweryfikuj hipotezę o istotności współczynnika kierunkowego funkcji regresji produkcji względem zatrudnienia.
d) Na poziomie istotności 0,05 zweryfikuj hipotezę o istotności współczynnika kierunkowego funkcji regresji zatrudnienia względem produkcji.
Zadanie 10.30
Uzbierane kwoty (w mln USD) Wielkiej Orkiestry Świątecznej Pomocy w latach 1998 - 2005 przedstawia poniższa tabela.
Rok |
Kwota zebranych pieniędzy w mln USD |
1998 |
3,54 |
1999 |
4,52 |
2000 |
6,09 |
2001 |
6,11 |
2002 |
6,85 |
2003 |
7,7 |
2004 |
6,92 |
2005 |
9,86 |
Źródło: www.wosp.org.pl
Wyznacz parametry liniowej funkcji trendu. Na poziomie istotności ![]()
sprawdź czy współczynnik kierunkowy wyznaczonej liniowej funkcji trendu jest statystycznie istotny.
215
Wyszukiwarka