Liczby zespolone

Definicja. Parę
nazywamy liczbą zespoloną, zaś
jednostką urojoną.

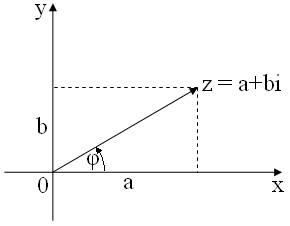
Zbiór
nazywamy zbiorem liczb zespolonych. Płaszczyznę z układem prostokątnych współrzędnych
nazywamy płaszczyzną zespoloną, jeśli każdy wektor o początku w (0,0) i końcu
reprezentuje liczbę zespoloną
.

Uwagi. Każdą liczbę zespoloną można zapisać w dwóch postaciach:
.

Definicja. Dane są liczby zespolone
oraz
. Wówczas
,
,
,

Jeśli
, to a nazywamy częścią rzeczywistą, b zaś częścią urojoną liczby zespolonej z, czyli
, modułem nazywamy nieujemną liczbę rzeczywistą
, zaś kąt
nazywamy argumentem liczby z: jest to kąt skierowany
jaki tworzy wektor reprezentujący liczbę z z osią OX.

Uwagi. Jeśli
i
, to
. Zbiór liczb rzeczywistych jest zatem częścią zbioru liczb zespolonych, tzn. każda liczba rzeczywista a jest liczbą zespoloną
ale oczywiście nie na odwrót. Liczby zespolone postaci
nazywają się liczbami urojonymi. Ponieważ liczby zespolone można traktować jako wielomiany, działania na liczbach zespolonych można traktować jak zwykłe działania na wielomianach: tak rozumiane działania pokrywają się z definicją wyżej (ZD).

Wszystkie wzory skróconego mnożenia dla liczb rzeczywistych, wzory na potęgowanie, wzory Vieta dla trójmianu kwadratowego itd. pozostają słuszne dla liczb zespolonych.

Twierdzenie. Dla dowolnych liczb zespolonych
:

1.
(przemienność dodawania i mnożenia),

2.
,
(łączność dodawania i mnożenia),

3.
(rozdzielność mnożenia względem dodawania).

Przykłady.

Definicja. Liczbą sprzężoną z liczbą zespoloną
nazywamy liczbę

Uwagi. Liczby zespolone sprzężone są reprezentowane przez punkty na płaszczyźnie, symetryczne względem osi OX. Zauważmy, że liczby sprzężone mają następujące własności:

,
.

Przykłady.

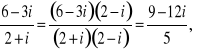
Pierwiastek stopnia drugiego z liczby zespolonej

Definicja.
wtedy i tylko wtedy, gdy

Przykłady

1. Obliczamy
.

, a zatem należy rozwiązać w liczbach rzeczywistych układ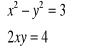
. Są dwa rozwiązania: (-2,-1) i (2,1). Zatem istnieją dwa szukane pierwiastki:
.

2. Obliczyć
(ZD).

3. Obliczyć
(ZD).

Rozwiązywanie równań w liczbach zespolonych

Niech dane będzie równanie algebraiczne

(4.4)
,

gdzie
.

Twierdzenie (Zasadnicze tw. Algebry). Równanie algebraiczne (4.4) ma w zbiorze C dokładnie n pierwiastków.

Definicja. Pierwiastniki równania algebraicznego
są to wzory na wszystkie pierwiastki tego rownania.

Twierdzenie. Nie istnieją pierwiastniki dla równań stopnia
.

Uwagi. Łatwo udowodnić (ZD), że jeśli
, to
(jeśli z jest pierwiastkiem równania, to jego sprzężenie też jest). Analogiczne twierdzenie dla zbioru
nie jest prawdziwe: wiadomo wtedy tylko tyle, że wielomian n-tego stopnia ma co najwyżej n pierwiastków rzeczywistych. Jak wiadomo istnieją pierwiastniki dla równań (4.4) stopnia 1., 2. (wzory Vieta), 3. (wzory Cardano) i 4. . Trójmian kwadratowy ma zawsze 2 pierwiastki: albo oba rzeczywiste albo oba zespolone i sprzężone ze sobą. Równanie 3. stopnia ma zawsze co najmniej jeden pierwiastek rzeczywisty i może mieć: trzy pierwiastki rzeczywiste albo jeden rzeczywisty i dwa zespolone sprzężone.

4. Obliczając ze wzorów Vieta rozwiązania równania
, dostajemy
(
).

Zauważmy, że powyższa metoda jest skuteczna tylko dla pierwiastków 2. stopnia. Przy np. obliczaniu pierwiastków 3. stopnia odpowiedni układ rownań będzie nieliniowy i 3. stopnia: będą trudności z jego rozwiązaniem.

5. Rozwiążemy równanie
.

Mamy
, skąd

6. Wielomian
rozkładamy na czynniki stopnia pierwszego:

.

Twierdzenie. Właściwości modułu:

1.

2.

3.

Dowód.

1.
,
.

2.
.

3. Jeżeli
, to
oraz
. KD.

Interpretacja geometryczna sumy i różnicy liczb zespolonych

Z postaci wektorowej liczb zespolonych (rys. ??) widać, że ich dodawanie [odejmowanie] sprowadza się do dodawania [odejmowania] wektorów reprezentujących te liczby. Moduł różnicy liczb zespolonych
jest równy odległości między punktami
na płaszczyźnie zespolonej (rys. ??).

Przykłady.

1. Równanie
przedstawia zbiór wszystkich z, których odległość od początku układu współrzędnych wynosi 1. Jest to więc okrąg o środku w początku układu i promieniu równym 1. Istotnie: jeżeli
, to
, a więc równanie
jest równoważne równaniu
, czyli
.

2. Równanie
przedstawia okrąg o środku w punkcie i, mający promień 1. Równanie tego okręgu we współrzędnych prostokątnych ma postać
.

3. Równanie
, gdzie
są punktami stałymi, a z jest punktem zmiennym, przedstawia zbiór wszystkich punktów równoodległych od
i
.

4. Równanie
, gdzie a i c oznaczają stałe dodatnie, jest równaniem elipsy, bo z tego równania odczytujemy, że określono zbiór punktów, których suma odległości od dwóch stałych punktów c i -c i jest wielkością stałą (równą 2a).

5. Zbiór takich punktów z, że
, oznacza wnętrze i brzeg koła o promieniu r i środku w punkcie
.

Postać trygonometryczna liczby zespolonej

!!!!!!!!BRAK RYSUNKU

Niech
. Wówczas
i
.

Definicja. Jeśli
, to

,

gdzie
, nazywamy jej postacią trygonometryczną.

Przykłady. Postać trygonometryczna liczby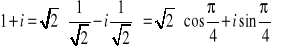
.

Postać trygonometryczna liczby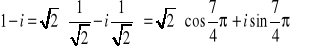
.

Dane są dwie liczby zespolone
oraz
.

Zatem
,
,
. Obliczamy iloczyn

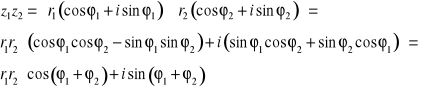
A więc mamy
.

Twierdzenie. Mnożenie liczb zespolonych sprowadza się więc do mnożenia ich modułów oraz dodawania ich argumentów:

(3.3)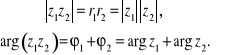

Danych jest n liczb zespolonych

. . . . . . . . . . . . . . . . . . . .

Uogólniając wzory (3.3) metodą indukcji matematycznej dostajemy

.

Twierdzenie.

.

Jeżeli w szczególności
a więc
oraz
, czyli
, to

Dla r = 1 mamy tzw. wzór Moivre'a:

Twierdzenie (Wzór Moivre'a).
.

Przykłady.

1. Obliczamy:

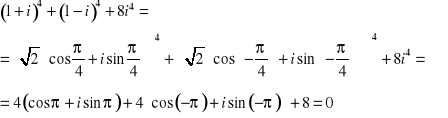
2.Obliczyć

Ponieważ
więc

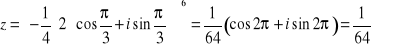
3. Zgodnie z wzorem Moivre'a

Po lewej stronie wykonujemy potęgowanie i otrzymujemy

Porównując części rzeczywiste i urojone po obu stronach równości dostajemy wzory wyrażające funkcje trygonometryczne kąta potrójnego przez funkcje kąta pojedynczego: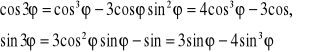

oraz wzór na
(ZD).

Niech
oraz
. Wówczas

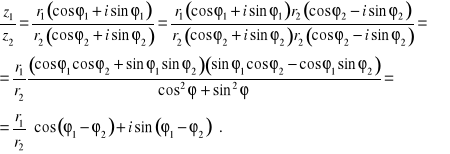
Zatem prawdziwe jest następujące

Twierdzenie.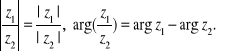

Pierwiastki dowolnego stopnia z liczb zespolonych

Definicja. Pierwiastkiem stopnia n z dowolnej liczby zespolonej z nazywamy taką liczbę u, że
. Zatem
.

Wyprowadzimy teraz wzory na takie pierwiastki. Wykorzystamy postać trygonometryczną liczby zespolonej. Niech

,

Jeżeli

(1)
,

to z definicji pierwiastka stopnia n mamy

lub (na podstawie wzoru Moivre'a)

(2)

Ale dwie liczby zespolone, w postaci trygonometrycznej, są sobie równe wtedy i tylko wtedy, gdy mają jednakowe moduły, a różnica ich argumentów jest wielokrotnością 2π. Zatem równość (2) jest spełniona, gdy

oraz
dla

stąd
(jest to pierwiastek arytmetyczny) oraz
.

Podstawiając do (1), dostajemy

(3)
,

gdzie wystarczy przyjąć
, gdyż dla innych całkowitych wartości k otrzymujemy kąty różniące się o wielokrotność 2π od kątów wyznaczonych poprzednio dla
Zatem każda liczba zespolona ( w szczególności również liczba rzeczywista) ma dokładnie n różnych pierwiastków zespolonych stopnia n, które obliczamy według wzoru (3), podstawiając za k kolejno liczby
. Zauważmy, że pierwiastek po prawej stronie (3) jest zwykłym arytmetycznym pierwiastkiem rzeczywistym, zaś symbol
po zespolonym pierwiastku na lewej stronie (3) oznacza, że pierwiastek ten jest obliczony dla wartości k występujące po prawej stronie (3).

Przykłady.

1. Obliczyć
.

Mamy dla k = 0, 1, 2, 3:

,

a zatem

.

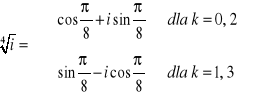
2. Jeżeli a jest liczbą rzeczywista dodatnią, to
, skąd:

.

(
po prawej stronie wzoru jest pierwiastkiem arytmetycznym).

3. Obliczyć
.

Mamy
skąd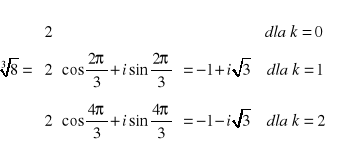
.

Ponieważ
oraz
, więc

(4)

Oznaczmy kolejne wartości wyznaczone wzorem (4) przez
Wzór na pierwiastki stopnia n z 1 przyjmuje wtedy postać

(4')

Wynikają stąd następujące własności liczb
:

1.Ponieważ
, więc wszystkie liczby (4') reprezentują na płaszczyźnie Gaussa punkty leżące na okręgu jednostkowym albo też wektory wychodzące z punktu (0,0) i mające długość 1.

2. Dla k = 0 mamy
, a więc jednym z pierwiastków dowolnego stopnia z liczby 1 jest zawsze 1, tzn. punkt przecięcia wspomnianego okręgu z dodatnią częścią osi rzeczywistej.

3.Łatwo zauważyć, że
tzn., że argumentem liczby
jest k-krotność liczby 2π/n, czyli n-tej części kąta pełnego.

Liczby z_k można więc znaleźć graficznie, dzieląc okrąg jednostkowy na n równych części, począwszy od punktu przecięcia tego okręgu z dodatnią częścią osi rzeczywistej. Innymi słowy, liczby z_k są wierzchołkami wielokąta foremnego o n bokach, wpisanego w okrąg jednostkowy, przy czym jednym z wierzchołków jest punkt 1.

8

---