2.Teoria zjawiska
Emisja elektronów z metalu (lub półprzewodnika) polega na uwalnianiu z jego powierzchni elektronów pod wpływem zewnętrznego czynnika pobudzającego. Takim czynnikiem może być wysoka temperatura (termoemisja), promieniowanie elektromagnetyczne (fotoemisja), wysokie napięcie (emisja polowa lub zimna) lub bombardujące cząstki, np. elektrony, jony.
Przedmiotem tego ćwiczenia jest badanie termoemisji w diodzie próżniowej. Dioda jest najprostszą lampą elektronowa -jest to lampa dwuelektrodowa. Jej elektrody (katoda i anoda) znajdują się w bańce szklanej, w której wytworzono wysoką próżnię. Aby wywołać termoemisję elektronów, katodę diody podgrzewa się elektrycznie. Rozróżnia się dwa rodzaje katod: żarzone bezpośrednio oraz żarzone pośrednio. W pierwszym przypadku katodę stanowi cienki drucik metalowy (najczęściej wolfram), który żarzy się w efekcie przepływającego przezeń prądu. W drugim przypadku katoda ma postać rurki metalowej (najczęściej pokrytej tlenkami), a grzejnik elektryczny jest umieszczony wewnątrz niej i od katody jest izolowany elektrycznie. Anoda diody na ogół ma postać cylindra otaczającego katodę.
Termoemisja elektronów - równanie Richardsona-Dushmana
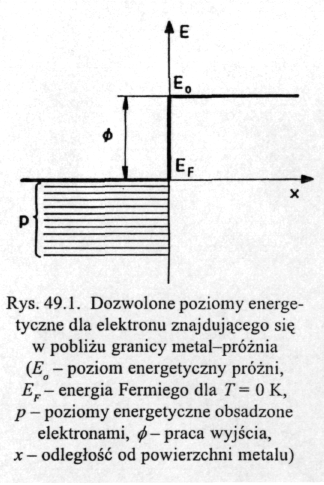
Elektrony wewnątrz metalu można rozpatrywać jako cząstki znajdujące się w studni potencjału o skończonej wysokości. Zgodnie z zakazem Pauliego, w temperaturze zera bezwzględnego (T=0K), elektrony zajmują wszystkie najniższe dozwolone poziomy energetyczne, aż do pewnej energii maksymalnej, zwanej energią Fermiego (EF). Aby elektron mógł opuścić metal musi pokonać barierę energetyczną istniejącą na granicy metal-próżnia (patrz rys. l). Dla elektronów znajdujących się na poziomie Fermiego wysokość tej bariery wynosi = E0 - Ef przy czym Eo jest energią elektronu o energii kinetycznej równej zero, z dala od powierzchni metalu. Praca wyjścia jest najmniejszą energią, jaką należy dostarczyć elektronowi znajdującemu się na poziomic Fermiego, aby mógł opuścić powierzchnię metalu. Inaczej mówiąc, aby elektron mógł opuścić powierzchnię metalu, składowa jego prędkości w kierunku prostopadłym do powierzchni katody musi spełniać warunek:
W termoemisji źródłem energii dostarczanej elektronom, koniecznej do pokonania powierzchniowej bariery potencjału, są drgania cieplne sieci krystalicznej, a warunek (1) w praktyce spełniony jest w wysokich temperaturach, np. dla wolframu w temperaturze rzędu 1000 K.
Zjawisko termoemisji ilościowo opisane zostało przez Richardsona i Dushmana równaniem:
w którym:
jest stałą Richardsona, T-temperaturą, s - powierzchnią katody, k— stałą Boltzmanna, R - współczynnikiem odbicia elektronów od bariery na granicy metal-próżnia, m - masą elektronu, e - ładunkiem elektronu a h - stałą Plancka. Równanie Richardsona określa natężenie prądu termoemisji w funkcji temperatury i pracy wyjścia, a więc ilość elektronów przechodzącą w jednostce czasu przez barierę na granicy metal-próżnia o wysokości w funkcji temperatury. Ze wzoru Richardsona-Dushmana wynika, że natężenie prądu termoemisji silnie zależy zarówno od temperatury, jak i od pracy wyjścia elektronów z katody. Przykładlowo, zwiększenie temperatury katody wolframowej (= 4,54 eV) od 1000K do 2000K, powoduje zwiększenie prądu tennoemisji około l08 razy, zaś pokrycie jej jednoatomową warstwą cezu (= 1,26 eV) powoduje, w temperaturze 1000 K, zwiększenie prądu termoemisji aż l016 razy.
Wyznaczanie temperatury pracy katody tlenkowej
Temperatura powierzchni katody tlenkowej pośrednio żarzonej jest niższa niż temperatura grzejnika, dlatego nie można jej określić metodą podaną w punkcie 49.2.3. Temperatury katody określa się z pomiarów Ia=j(Ua). W tym przypadku na elektrony działa pole hamujące (Ua< 0), a przepływ prądu określa równanie które można przedstawic w postaci
Z równania tego otrzymujemy temperaturę katody tlenkowej
Obrazem graficznym tego równania na wykresie In Ia=J(Ua) jest linia prosta, której współczynnik kierunkowy (nachylenie) wynosi
gdzie: e - ładunek elektronu, k - stała Boltzmanna
3.Wyprowadzenie stosownego wzoru
Elektrony przebywają różnicę potencjału U,i pole elektryczne wykonuje pracę równą:
![]()
Pracę tę wykonują kosztem energii kinetycznej
![]()
Do anody mogą dojść tylko elektrony o dostatecznej dużej energii, przekraczającej pracę przeciw potencjałowi hamowania
![]()
e -nabój elektronów;
![]()
- potencjał hamujący;
Ze wzrostem ujemnego potencjału anody, liczba elektronów o energii wystarczającej do pokonania potencjału hamującego anody jest coraz mniejsza i prąd w obwodzie anodowym maleje .Przy pewnej wartości:![]()
żaden z elektronów nie dochodzi do anody.
![]()
4. Wyniki pomiarowe iszacowanie niepewności:
dla
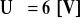
|
U |
I [ |
ln( |
1. |
0 |
1,6 |
0 |
2. |
0,05 |
1,27 |
0,230987 |
3. |
0,1 |
0,94 |
0,531879 |
4 |
0,15 |
0,73 |
0,784714 |
5 |
0,2 |
0,51 |
1,143348 |
6 |
0,25 |
0,37 |
1,464256 |
7 |
0,3 |
0,23 |
1,93968 |
8 |
0,35 |
0,15 |
2,367124 |
9 |
0,4 |
0,08 |
2,995732 |
10 |
0,5 |
0,03 |
3,976562 |
11 |
0,6 |
0,01 |
5,075174 |
12 |
0,7 |
0 |
…… |
13 |
0,8 |
0 |
......... |
14 |
0,9 |
0 |
......... |
Maksymalne prędkości elektronów obliczam ze wzoru:
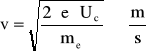
e - ładunek elementarny ![]()
[C]
![]()
-masa elektronu
napięcie hamowania ![]()
dla ![]()
v = 459395,28 [m/s]
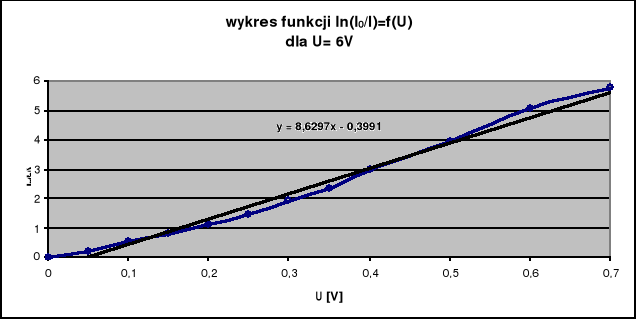
Temperaturę żarzenia obliczam ze wzoru:
![]()
e - ładunek elektryczny ![]()
[C]
k- stała Boltzmana ![]()
[J/K]
a - współczynnik kierunkowy prostej ln(I0/I)==f(U)
T=1345,20 [K]
Szacowanie niepewności pomiarów dla v:
![]()
[C] - z tablic fizycznych
![]()
[kg] -z tablic fizycznych
![]()
wartości pochodnych cząstkowych:
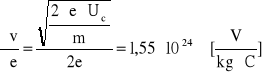
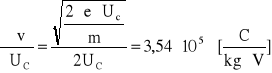
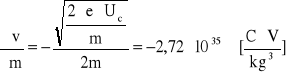
Obliczam niepewność całkowitą:
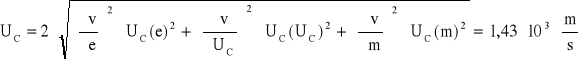
![]()
Szacowanie niepewności pomiarowych dla T:
![]()
- z tablic fizycznych
![]()
- z tablic fizycznych
![]()
- obliczony przez program matlab
wartości pochodnych:
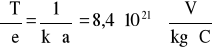
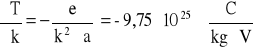
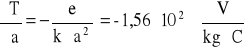
niepewność całkowitą obliczam:
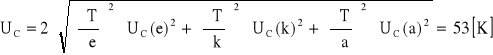
![]()
b) dla ![]()
|
U |
I [ |
ln( |
1 |
0 |
24 |
0 |
2 |
0,05 |
18 |
0,287682 |
3 |
0,1 |
14 |
0,538997 |
4 |
0,15 |
10 |
0,875469 |
5 |
0,2 |
7 |
1,232144 |
6 |
0,25 |
5 |
1,568616 |
7 |
0,3 |
3 |
2,079442 |
8 |
0,4 |
1 |
3,178054 |
9 |
0,5 |
0,5 |
3,871201 |
10 |
0,6 |
0,25 |
4,564348 |
11 |
0,7 |
0,1 |
5,480639 |
12 |
0,8 |
0 |
....... |
13 |
0,9 |
0 |
....... |
Maksymalne prędkości elektronów obliczam ze wzoru:
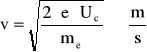
e - ładunek elementarny
![]()
-masa elektronu
napięcie hamowania ![]()
dla ![]()
v = 530463,98 [m/s]
Temperaturę żarzenia obliczam ze wzoru:
![]()
e -ładunek elektryczny ![]()
[C]
k- stała Boltzmana ![]()
[J/K]
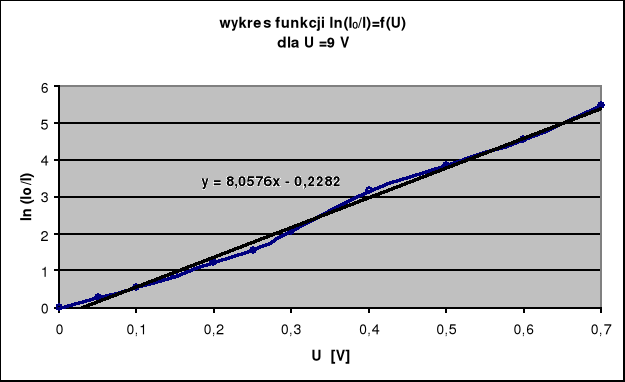
a - współczynnik kierunkowy prostej ln(I0/I)==f(U)
T=1440,71 [K]
Szacowanie niepewności pomiarów dla v:
![]()
[C] - z tablic fizycznych
![]()
[kg] -z tablic fizycznych
![]()
wartości pochodnych cząstkowych:
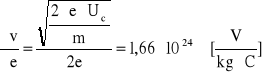
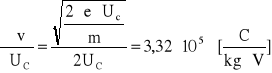
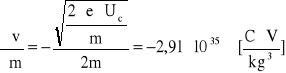
Obliczam niepewność całkowitą:
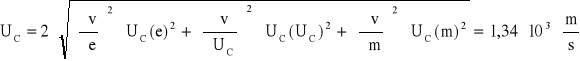
![]()
Szacowanie niepewności pomiarowych dla T:
![]()
- z tablic fizycznych
![]()
- z tablic fizycznych
![]()
- obliczony przez program matlab
wartości pochodnych:
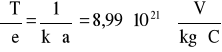
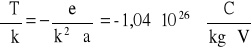
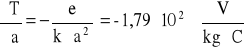
niepewność całkowitą obliczam:
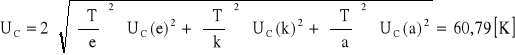
![]()
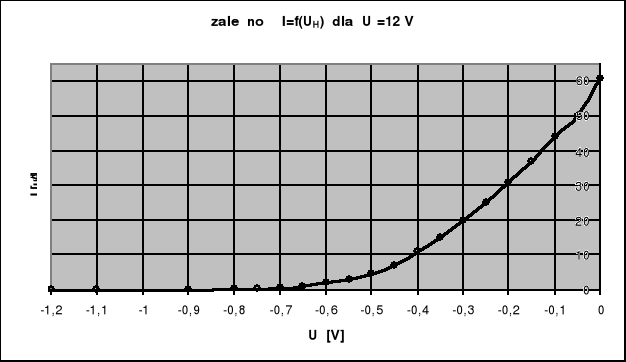
c) dla ![]()
|
U |
I [ |
ln( |
1 |
0 |
61 |
0 |
2 |
0,05 |
50 |
0,198851 |
3 |
0,1 |
44 |
0,326684 |
4 |
0,15 |
37 |
0,499956 |
5 |
0,2 |
31 |
0,676887 |
6 |
0,25 |
25 |
0,891998 |
7 |
0,3 |
20 |
1,115142 |
8 |
0,35 |
15 |
1,402824 |
9 |
0,4 |
11 |
1,712979 |
10 |
0,45 |
7 |
2,164964 |
11 |
0,5 |
4,5 |
2,606796 |
12 |
0,55 |
3 |
3,012262 |
13 |
0,6 |
2 |
3,417727 |
14 |
0,65 |
1 |
4,110874 |
15 |
0,7 |
0,5 |
4,804021 |
16 |
0,75 |
0,3 |
5,314847 |
17 |
0,8 |
0,25 |
5,497168 |
18 |
0,9 |
0,1 |
6,413459 |
19 |
1,1 |
0 |
...... |
20 |
1,2 |
0 |
...... |
Maksymalne prędkości elektronów obliczam ze wzoru:
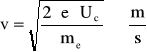
e - ładunek elementarny
![]()
-masa elektronu
napięcie hamowania ![]()
dla ![]()
v = 622024,15 [m/s]
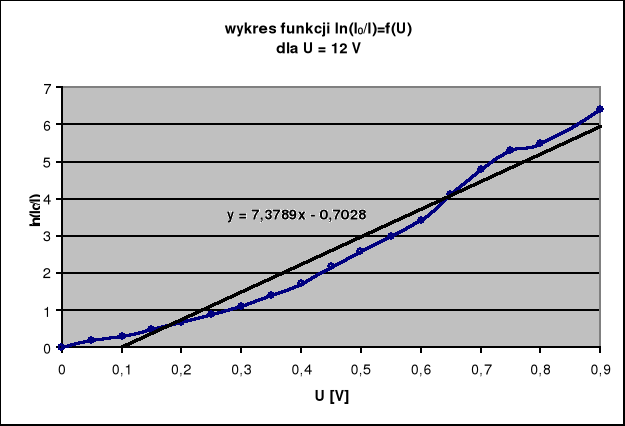
Temperaturę żarzenia obliczam ze wzoru:
![]()
e -ładunek elektryczny
k- stała Boltzmana
a - współczynnik kierunkowy prostej ln(I0/I)==f(U)
T=1573,23 [K]
Szacowanie niepewności pomiarów dla v:
![]()
[C] - z tablic fizycznych
![]()
[kg] -z tablic fizycznych
![]()
wartości pochodnych cząstkowych:
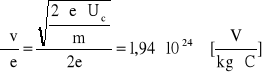
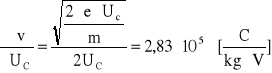
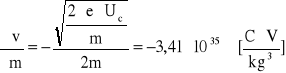
Obliczam niepewność całkowitą:
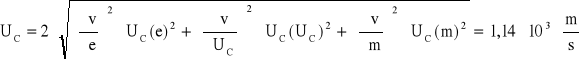
![]()
Szacowanie niepewności pomiarowych dla T:
![]()
- z tablic fizycznych
![]()
- z tablic fizycznych
![]()
- obliczony przez program matlab
wartości pochodnych:
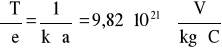
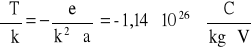
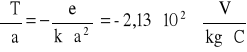
niepewność całkowitą obliczam:
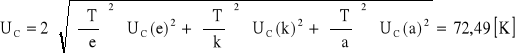
![]()
Wnioski:
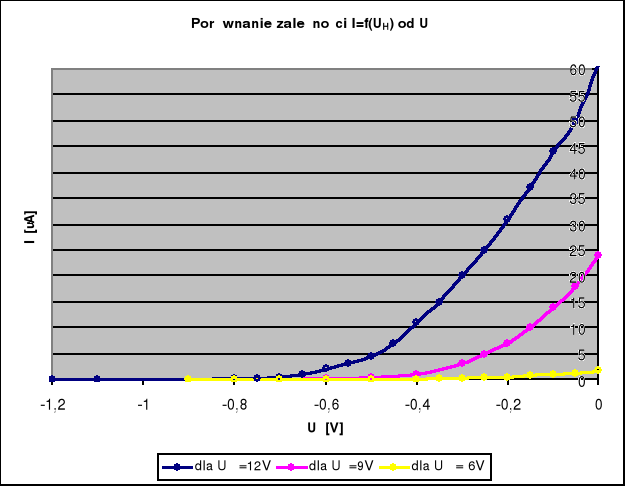
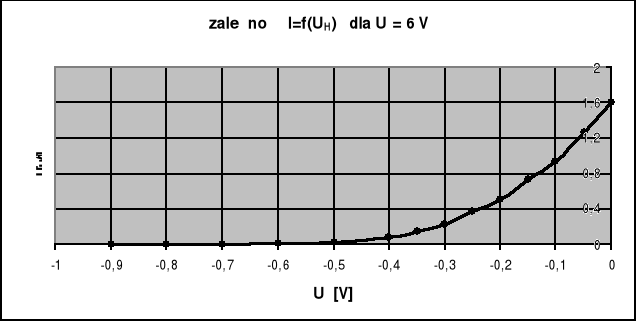
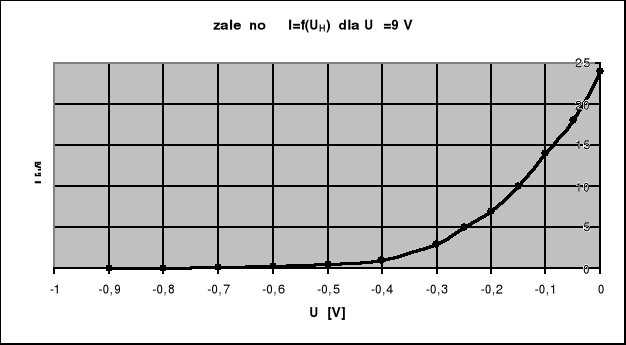
Celem powyższego ćwiczenia było wyznaczenie maksymalnych prędkości wyjściowych elektronów emitowanych przez termokatodę oraz wyznaczeniu temperatury żarzenia termokatody. Całkowity pomiar polegał na wyznaczeniu natężenia płynącego prądu w układzie dla zmieniającego się napięcia hamowania. Pomiarów tych należało dokonać przy napięciu w układzie włókna grzejnego katody 12V, 9V, 6 V.
Wyszukiwarka